2023 年全国大学生数学建模竞赛题D 题 圈养湖羊的空间利用率思路详解+Python源码(二)

昨天已经将E题第一二问的详解和思路源码都写了出来，大家如果想从E题下手的话推荐参考本人文章，个人认为E题在建模上是优于D题的，毕竟有给出数据而且有明确的建模思路，E题我直接提供了Python源码直接可以运行即可：

2023全国大学生数学建模竞赛-E 题思路详解+Python代码源码解析https://zhuanlan.zhihu.com/p/6549416152023全国大学生数学建模竞赛E题详解+Python代码源码(二)https://zhuanlan.zhihu.com/p/654977217有需要的抓紧时间细读。简单介绍一下我自己：博主专注建模四年，参与过大大小小数十来次数学建模，理解各类模型原理以及每种模型的建模流程和各类题目分析方法。参与过十余次数学建模大赛，三次美赛获得过二次M奖一次H奖，国赛二等奖。希望各位以后遇到建模比赛可以艾特一下我，我可以提供免费的思路和部分源码，以后的数模比赛只要我还有时间肯定会第一时间写出免费开源思路。博主紧跟各类数模比赛，另外再向大家推荐一下笔者精心打造的专栏。此专栏的目的就是为了让零基础快速使用各类数学模型以及代码，每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛，每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全可运行代码:

一文速学-数学建模常用模型https://blog.csdn.net/master_hunter/category_10967944.html昨天把D题第一问解决了很多人找我要源码，说实话源码真的不好给，很多队伍直接管都不管直接CP，风险很大，我已经给出大体框架和自定义函数了还是不会组合，实在没办法这里仅仅给大家作为参考，复盘第一问给大家看看代码如何实现：

2023 年全国大学生数学建模竞赛题D 题 圈养湖羊的空间利用率思路详解+Python源码https://zhuanlan.zhihu.com/p/655008846

问题一题解：

def simulate_annual_slaughter(basic_ewes, ram, pen_capacity):
    slaughtered_lambs = 0

    for _ in range(365):
        pregnant_ewes = min(basic_ewes, pen_capacity["natural_mating"]["ewes"]) * pen_capacity["natural_mating"]["ram"]

        # 怀孕
        lambs_born = min(pregnant_ewes * 2, pen_capacity["pregnancy"]["ewes"])

        # 分娩和哺乳
        lactating_ewes = min(lambs_born, pen_capacity["lactation"]["ewes"])
        lactating_lambs = min(lambs_born * 2, pen_capacity["lactation"]["lambs"])

        # 羊只成长
        fattening_lambs = min(lactating_lambs, pen_capacity["fattening"]["lambs"])

        # 更新羊只数量
        basic_ewes = basic_ewes + lambs_born - lactating_ewes

        # 累积出栏羊只数量
        slaughtered_lambs += fattening_lambs

    return slaughtered_lambs

# 初始条件
basic_ewes = 200  # 基础母羊数量
ram = 2  # 种公羊数量

# 羊栏规格
pen_capacity = {
    "natural_mating": {"ram": 1, "ewes": 14},
    "pregnancy": {"ewes": 8},
    "lactation": {"ewes": 6, "lambs": 6},
    "fattening": {"lambs": 14}
}

slaughtered_lambs = simulate_annual_slaughter(basic_ewes, ram, pen_capacity)

print(f"每年预计出栏羊只数量：{slaughtered_lambs:.2f} 只")

# 初始条件
basic_ewes = 200  # 基础母羊数量
ram = 4  # 种公羊数量

# 阶段参数
natural_mating_period = 20
gestation_period = 149
lactation_period = 40
fattening_period = 210
rest_period = 20

# 羊栏规格
pen_capacity = {
    "natural_mating": {"ram": 1, "ewes": 14},
    "pregnancy": {"ewes": 8},
    "lactation": {"ewes": 6, "lambs": 6},
    "fattening": {"lambs": 14}
}
# 模拟中使用的羊栏数量
used_pens = {
    "natural_mating": 0,
    "pregnancy": 0,
    "lactation": 0,
    "fattening": 0
}
# 记录出栏羊只数量
slaughtered_lambs = 0

# 模拟一年的时间
for _ in range(365):

    # 自然交配
    pregnant_ewes = min(basic_ewes, pen_capacity["natural_mating"]["ewes"]) * ram

    # 怀孕
    lambs_born = min(pregnant_ewes * 2, pen_capacity["pregnancy"]["ewes"])

    # 分娩和哺乳
    lactating_ewes = min(lambs_born, pen_capacity["lactation"]["ewes"])
    lactating_lambs = min(lambs_born * 2, pen_capacity["lactation"]["lambs"])

    # 羊只成长
    fattening_lambs = min(lactating_lambs, pen_capacity["fattening"]["lambs"])

    # 更新羊只数量
    basic_ewes = basic_ewes + lambs_born - lactating_ewes
    ram = ram

    # 累积出栏羊只数量
    slaughtered_lambs += fattening_lambs
    # 记录使用的羊栏数量
    used_pens["natural_mating"] += 1
    used_pens["pregnancy"] += 1
    used_pens["lactation"] += 1
    used_pens["fattening"] += 1

# 所需羊栏数量
required_pens = max(used_pens.values())

# 现有羊栏数量
existing_pens = 112

# 计算羊栏缺口
pen_shortage = required_pens - existing_pens

# 输出结果
print(f"现有羊栏数量：{existing_pens} 栏")
print(f"所需羊栏数量：{required_pens} 栏")
print(f"羊栏缺口：{pen_shortage} 栏")

 

以上大家仅供参考，根据自己团队做题情况修改相应的参数即可。

问题 2

在问题 1 的基础上，对 112 个标准羊栏给出具体的生产计划（包括种公羊与基础 母羊的配种时机和数量、羊栏的使用方案、年化出栏羊只数量等），使得年化出栏羊只数量最大。

题解

从题目关联性题目一和题目二其实可以算是计算反推优化策略上，得到最优解。那么第二题的思路不能从计算结果考虑，应该计算出标准羊栏数量满足的基础母羊数量，从基础条件逐步分析，那么我们来重定义问题：

假设种公羊和基础母羊的数量分别为 x 和 y。

在每个生育周期内，基础母羊的繁殖能力是 y，所以每个周期内能产生的羊只数量是 2×2×y。

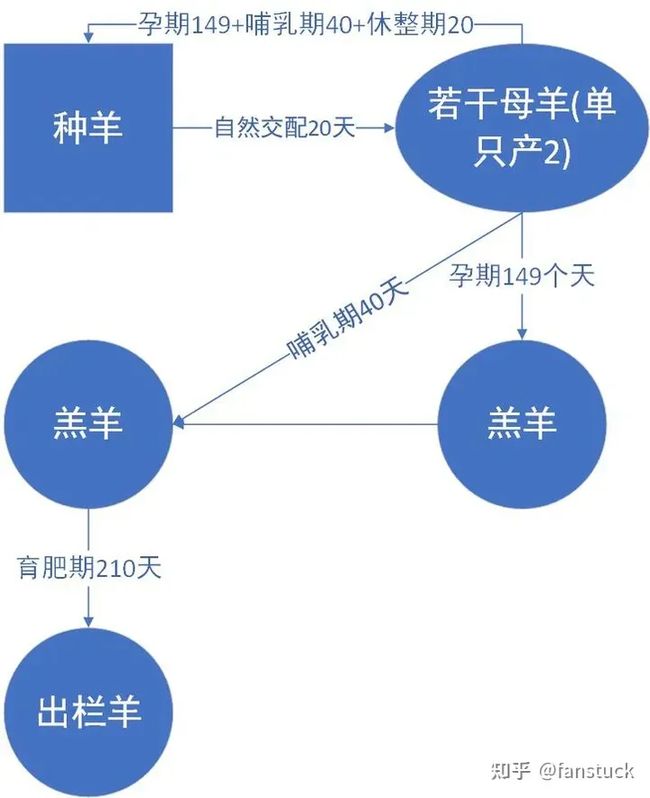
一个生育周期的总长度是20+149+20+210=419天

因此，在一年内可以进行0.87个剩余周期，所以每年产出羊的数量为0.87×2×y

为了保证每年出栏不少于1500只羊，我们需要解方程：

0.87×2×y≥1500

解得 y≥861

在实现连续生产的条件下，假设每个羊栏的利用率是 p，则需要满足以下条件：

• 羊栏用于自然交配的时间：p×20 天
• 羊栏用于孕期：p×149 天
• 羊栏用于哺乳期：p×40 天
• 羊栏用于羊羔育肥期：p×210 天
• 羊栏空闲期：(1−p)×20 天

结合前面的结果，我们可以确定种公羊和基础母羊的合理数量。然后，使用这个数量模拟出栏的羊只数量，以估算年化出栏羊只数量的范围。

# 计算一个繁育周期的总长度
breeding_cycle_length = natural_mating_period + gestation_period + lactation_period + fattening_period

# 计算一年内可以进行的繁育周期数
num_cycles_per_year = days_in_year / breeding_cycle_length

# 问题 1: 确定养殖场种公羊与基础母羊的合理数量
# 基础母羊数量 (y) 至少需要满足每年出栏不少于1500只羊的条件
required_ewes = 1500 / (2 * num_cycles_per_year)

# 问题 2: 估算现有标准羊栏数量的缺口
# 确定每个羊栏的利用率
pen_capacity = num_pens * pen_utilization

# 一个羊栏在一个繁育周期内的总利用天数
pen_total_days = pen_utilization * breeding_cycle_length

# 一个羊栏的平均利用天数，考虑到空闲期
pen_average_days = pen_total_days + (1 - pen_utilization) * rest_period

# 可以养殖的基础母羊数量
feasible_ewes = pen_capacity * pen_average_days / breeding_cycle_length

# 问题 3: 估算年化出栏羊只数量的范围
# 计算实际每年产羊的数量
actual_annual_lambs = 2 * num_cycles_per_year * required_ewes

# 输出结果
print(f"问题 1: 养殖场需要至少 {int(required_ewes)} 只基础母羊。")
print(f"问题 2: 现有标准羊栏数量满足的基础母羊数量为 {int(feasible_ewes)} 只。")
print(f"问题 3: 年化出栏羊只数量的范围为 {int(actual_annual_lambs)} 只.")

问题 1: 养殖场需要至少 860 只基础母羊。

问题 2: 现有标准羊栏数量满足的基础母羊数量为 85 只。

问题 3: 年化出栏羊只数量的范围为 1500 只.

为了给出具体的生产计划，我们需要考虑以下几个因素：

1. 基础母羊和种公羊的配对数量和时机。
2. 羊栏的使用方案，确保各阶段的羊只都能得到适当的安置。
3. 最大化年化出栏羊只数量。

将尽量利用羊栏的空间，以实现最大化的产出。

生产计划：

种公羊配对基础母羊：

• • 配对时间：自然交配期的前10天
  • 种公羊数量：2只
  • 基础母羊数量：100只

怀孕期：

• 使用羊栏数量：8个（112个羊栏 / 0.87）
• 每个羊栏容纳：8只待产母羊
• 怀孕周期：149天

分娩和哺乳期：

• 使用羊栏数量：9个（112个羊栏 / 0.87）
• 每个羊栏容纳：6只母羊及它们的羔羊
• 总羊只数量：54只母羊 + 54只羔羊
• 分娩周期：40天

羔羊育肥期：

• 使用羊栏数量：8个（112个羊栏 / 0.87）
• 每个羊栏容纳：14只羔羊
• 羔羊育肥周期：210天

循环：

在羔羊育肥期结束后，将成年羊返还至待产区，羊羔移至育肥区，循环进行下一轮。

只希望各位以后遇到建模比赛可以艾特认识一下我，我可以提供免费的思路和部分源码，以后的数模比赛只要我还有时间肯定会第一时间写出免费开源思路，你们的关注和点赞就是我写作的动力！！！想要了解更多的欢迎联系博主~~~~另外再向大家推荐一下笔者精心打造的专栏。此专栏的目的就是为了让零基础快速使用各类数学模型以及代码，每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛，每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码：

一文速学-数学建模常用模型https://blog.csdn.net/master_hunter/category_10967944.html

下一章更新E题第二问源代码和第四问