力扣回溯算法专题(二)- 切割 子集问题 131.分割回文串、93. 复原IP地址、78. 子集、90. 子集Ⅱ、491.递增子序列 思路 C++实现 去重及其优化和注意点 总结
文章目录
- 切割问题
- 子集问题
- 回溯法模板与伪代码
- 131. 分割回文串
-
- 三要素及思路
- 回文字符串判断
- 代码
- 93. 复原IP地址
-
- 三要素及思路
- 验证子串是否合法
- 代码
- 78. 子集
-
- 三要素及思路
- 代码
- 90. 子集Ⅱ
-
- 三要素及思路
- 去重
- 代码
- 491.递增子序列
-
- 三要素及思路
- 去重方式及去重优化
- 代码
- 总结
-
- 1. 切割问题
- 2. 子集问题
切割问题
切割问题:一个字符串按一定规则有几种切割方式——131.分割回文串、93.复原IP地址
- 不同的切割问题有不同的切割方式
- 如何判断回文
- 如何验证区间合法
- 如何添加符号
切割问题类似组合问题,例如字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个…
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段…
子集问题
子集问题:一个N个数的集合里有多少符合条件的子集——78.子集、90.子集Ⅱ、491.递增子序列
- 如果把子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点
- 子集其实也是一种组合问题,因为它的集合是无序的,子集{1,2} 和子集{2,1}是一样的
- 集合无序,那么元素不能重复选取,写回溯算法时,for循环要从startIndex开始,而不是从0开始
- 去重方式,不同子集问题对应不同的去重逻辑,区别树层去重和树枝去重
回溯法模板与伪代码
//返回值一般为void 先写逻辑再确定参数
//一般搜到叶子节点也就找到了满足条件的一条答案,存放该答案并结束本层递归
//for循环横向遍历集合区间,for循环执行次数=一个节点孩子数:处理节点 递归 回溯
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
131. 分割回文串

三要素及思路
切割问题抽象为一棵树形结构:递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法

先写逻辑,再确定递归函数参数:
path,一维数组,存放已经回文的子串,全局变量
result,二维数组,存放子串集,全局变量
s,题目给的字符串
startindex,下一层for循环搜索的起始位置,递归的起始位置,相当于切割线,不能重复切割
终止条件: 找到切割方法就终止,即切割线到字符串最后面就结束本层递归
单层搜索:
- 切割的子串长度应该是[startindex, i]
- 首先,判断子串是否为回文字符串,是则存进path中,不是则跳过
- 然后递归、回溯,要注意不能重复切割,注意递归时的起始位置
回文字符串判断
判断回文-前后指针:
- 使用前后双指针
- 一个指针从前往后,一个从后往前,如果前后指针指向元素相等,说明是回文字符串
- 这部分代码重复性高,可以抽象为一个成员函数
判断回文-动态规划-优化:
- 给定一个字符串s,长度为n,它成为回文字串的充分必要条件是s[0] == s[n-1],且s[1:n-1]是回文字串
- 动态规划,数组存放子串是否为回文子串的结果,倒序计算
- 三种情况:
- n=1,只有一个字符,肯定是回文
- n=2,两个字符,如果两个字符相同就是回文,否则不是
- n>2,多个字符,如果s[0] == s[n-1],且s[1:n-1]也是回文,该字符串才是回文字符串
代码
- 前后双指针
class Solution {
public:
vector<string> path;
vector<vector<string>> result;
//前后指针判断回文字符串
//前指针从前往后 后指针从后往前 判断两指针元素是否相同
bool isPalindrome(const string& s, int start, int end)
{
for(int i=start, j=end; i<j; i++,j--)
{
if(s[i]!=s[j]) return false;
}
return true;
}
void backtracking(const string& s, int startindex)
{
//终止条件 说明分割线到字符串最后了 保存结果 结束本层递归
if(startindex >= s.size())
{
result.push_back(path);
return;
}
//单层搜索
for(int i=startindex; i<s.size(); i++)
{
//1.判断子串是否为回文子串 是则保存子串 否则跳过
if(isPalindrome(s, startindex, i)) path.push_back(s.substr(startindex, i-startindex+1));
else continue;
//递归 回溯
backtracking(s, i+1);//递归时不重复切割
path.pop_back();//回溯
}
}
vector<vector<string>> partition(string s) {
path.clear();
result.clear();
backtracking(s, 0);
return result;
}
};
- 动态规划
class Solution {
public:
vector<string> path;
vector<vector<string>> result;
//动态规划 二维布尔矩阵 判断回文字符串
vector<vector<bool>> isPalindrome; // 放事先计算好的是否回文子串的结果
void backtracking(const string& s, int startindex)
{
if(startindex >= s.size())//切割线到字符串最后 结束本层递归
{
result.push_back(path);
return;
}
for(int i=startindex; i<s.size(); i++)
{
//根据布尔矩阵 直接知道 当前长度切割的字符串是否为回文字符串
if(isPalindrome[startindex][i]) path.push_back(s.substr(startindex, i-startindex+1));//是回文
else continue;
backtracking(s, i+1);//递归
path.pop_back();//回溯
}
}
vector<vector<string>> partition(string s) {
path.clear();
result.clear();
computePalindrome(s);//获得当前字符串对应的布尔矩阵
backtracking(s, 0);
return result;
}
// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串
// 回文字串的充分必要条件是s[0] == s[n-1],且s[1:n-1]是回文字串
void computePalindrome(const string& s)
{
//根据字符串实际大小重新规划二维布尔矩阵大小 isPalindrome默认值是false
isPalindrome.resize(s.size(), vector<bool>(s.size(), false));
for(int i=s.size()-1; i>=0; i--)
{
//倒序赋值
for(int j=i; j<s.size(); j++)
{
if(j==i) isPalindrome[i][j]=true;//n=1,只有一个字符
else if(j-i==1) isPalindrome[i][j] = (s[i]==s[j]);//n=2,两个字符
else isPalindrome[i][j] = (s[i]==s[j] && isPalindrome[i+1][j-1]);//多个字符
}
}
}
};
93. 复原IP地址

三要素及思路
先写逻辑,再确定递归函数参数:
result,二维数组,存放子串集,全局变量
s,题目给的字符串
startindex,下一层for循环搜索的起始位置,递归的起始位置,相当于切割线,不能重复切割
pointnum,记录添加逗点的数量
终止条件: 题目要求数字串只能分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数=4作为终止条件。因此,当pointnum=3时,说明字符串分成了4段了,如果第四段合法就保存结果
单层搜索:
- 同样,切割的子串长度是[startindex, i]
- 需要判断这个子串是否合法
如果合法,就指定位置插入符号 . 表示已经分割,然后递归、回溯
如果不合法就结束本层循环,剪掉分支 - 递归时,不重复分割,下一层的起始位置是i+2,因为每一段后面加了符号 . ,并且pointnum要+1
- 回溯时,pointnum要-1,并且要删掉符号 .
剪枝: 如果数字串只有三个数字,或者超出12个数字,都不能构成合法的ip,剪枝
验证子串是否合法
抽象成一个成员函数,主要考虑三点
- 段位以0为开头的数字,不合法
- 段位里有非正整数字符,不合法
- 段位如果大于255了,不合法
代码
class Solution {
public:
vector<string> result;
//回溯
void backtracking(string& s, int startindex, int pointnum)
{
//终止条件 有四段,即pointnum=3终止本层递归
if(pointnum==3)
{
//第四段合法就保存结果 否则直接结束递归
if(isvalid(s, startindex, s.size()-1)) result.push_back(s);
else return;
}
//单层搜索
for(int i=startindex; i<s.size(); i++)
{
//子串区间是[startindex, i] 判断该子串是否合法,合法就处理,否则结束本层递归,进入下一层
if(isvalid(s, startindex, i))
{
//子串合法则在i后面插入. 更新符号数 然后递归 回溯
s.insert(s.begin()+i+1, '.');
pointnum++;//添加符号数+1
backtracking(s, i+2, pointnum);//递归 注意是i+2 因为加了.
pointnum--;//回溯
s.erase(s.begin()+i+1);//回溯 删除.
}
else break;
}
}
//验证字段合法性 s在左闭右闭区间[start, end]所组成的数字是否合法
bool isvalid(const string& s, int start, int end)
{
if(start > end) return false;//不合法区间
if(start!=end && s[start]=='0') return false;//段位以0为开头的数字,不合法 注意start != end
int num = 0;
for(int i=start; i<=end; i++)
{
if(s[i]<'0' || s[i]>'9') return false;//有非正整数字符,不合法
num = num*10 + (s[i]-'0');
if(num>255) return false;//如果大于255了,不合法
}
return true;
}
vector<string> restoreIpAddresses(string s) {
result.clear();
//如果数字串只有三位数字或者超过12个数字 不能构成合法ip
if(s.size()<4 || s.size()>12) return result;
backtracking(s, 0, 0);
return result;
}
};
78. 子集

求子集集合,也就是遍历树,保存所有节点
三要素及思路
先写逻辑,再确定递归函数参数:
path, 一维数组,保存符合条件的单个子集,全局变量
result,二维数组,存放子集集合,全局变量
nums,题目给的数组
startindex,下一层for循环搜索的起始位置,递归的起始位置,不能重复选取
终止条件:
- 子集问题遍历整棵树,for循环结束也表示遍历结束,可以不需要终止条件
- 遍历到叶子节点,剩余集合为空,说明遍历结束。相当于startindex大于数组长度,此时没有元素可取了,即
startIndex >= nums.size()
单层搜索: 收集元素、递归、回溯,注意递归时不重复选取元素
剪枝: 不需要任何剪枝,因为子集问题要遍历整棵树
代码
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void backtracking(const vector<int>& nums, int startindex)
{
result.push_back(path);//保存结果
if(startindex >= nums.size()) return;//终止条件 startindex大于数组长度 也可以不需要
//单层搜索
for(int i=startindex; i<nums.size(); i++)
{
path.push_back(nums[i]);
backtracking(nums, i+1);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
path.clear();
result.clear();
backtracking(nums, 0);
return result;
}
};
90. 子集Ⅱ
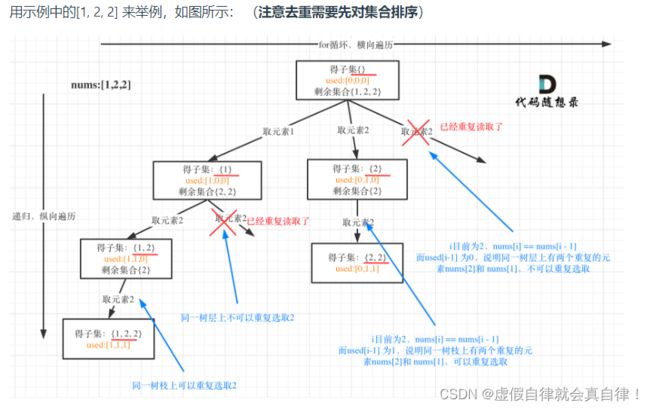
这道题目和78.子集的区别是,集合里有重复元素,而且求取的子集要去重
去重操作本质上和40. 组合总和Ⅱ是一样的做法,并且排列问题的去重也是同样的操作
着重理解树层去重和树枝去重,注意去重需要先对集合排序,具体可以看力扣回溯算法专题(一)的40. 组合总和Ⅱ的去重笔记
三要素及思路
先写逻辑,再确定递归函数参数:
path, 一维数组,保存符合条件的单个子集,全局变量
result,二维数组,存放子集集合,全局变量
nums,题目给的数组
startindex,下一层for循环搜索的起始位置,递归的起始位置,不能重复选取
终止条件:
- 子集问题遍历整棵树,for循环结束也表示遍历结束,可以不需要终止条件
- 遍历到叶子节点,剩余集合为空,说明遍历结束。相当于startindex大于数组长度,此时没有元素可取了,即
startIndex >= nums.size()
单层搜索: 先去重,再是收集元素、递归、回溯,注意递归时不重复选取元素,且去重前先排序
去重
1. 对同一父节点下本层的去重,有三种去重方式
- startindex来控制,当i>startindex时,如果nums[i]=nums[i-1],说明是重复元素,跳过
- bool型的标记数组used,注意区分什么时候是树枝,什么时候是树层
- set容器,要注意的是,set只记录本层元素是否重复使用,新的一层uset都会重新定义,相当于把上一层的记录清空。使用find查找,可以加快查找重复元素的速度,set是不允许存储相同元素的
2. set去重的注意点:
使用set去重时,要注意两点:
-
情况1:set不能定义放到类成员位置,然后模拟回溯的样子 insert一次,erase一次
-
情况2:set不能放到类成员位置,然后每次进入单层的时候用uset.clear()。
情况1 代码
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
unordered_set<int> uset; // 把uset定义放到类成员位置
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // 递归之前insert
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
uset.erase(nums[i]); // 回溯再erase
}
}

在树形结构中,如果把unordered_set uset放在类成员的位置,相当于全局变量,就把树枝的所有情况都记录了,不是仅控制某一节点下的同一层了。也就是说,一旦把unordered_set uset放在类成员位置,它控制的就是整棵树,包括树枝。所以不能这么写
情况2 代码
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
unordered_set<int> uset; // 把uset定义放到类成员位置
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
uset.clear(); // 到每一层的时候,清空uset
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // set记录元素
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
}
}
在这种写法情况下,uset已经是全局变量,本层的uset记录了一个元素,然后进入下一层之后这个uset(和上一层是同一个uset)就被清空了,也就是说,层与层之间的uset是同一个,那么就会相互影响。所以还不不能这么写
代码
- 通过startindex去重
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums, int startindex)
{
result.push_back(path);
for(int i=startindex; i<nums.size(); i++)
{
//去重 前后元素相同则跳过
if(i>startindex && nums[i]==nums[i-1]) continue;
path.push_back(nums[i]);
backtracking(nums, i+1);
path.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
path.clear();
result.clear();
//去重前先排序
sort(nums.begin(), nums.end());
backtracking(nums, 0);
return result;
}
};
- 通过bool型标记数组去重
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums, int startindex, vector<bool>& used)
{
result.push_back(path);
for(int i=startindex; i<nums.size(); i++)
{
//nums[i]==nums[i-1]时,
//如果used[i-1]==false,说明同一树层nums[i - 1]使用过
//如果used[i-1]==true,说明同一树枝nums[i - 1]使用过
if(i>0 && nums[i]==nums[i-1] && used[i-1]==false) continue;
else
{
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, i+1, used);
used[i] = false;
path.pop_back();
}
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums)
{
path.clear();
result.clear();
vector<bool> used(nums.size(), false);//默认元素不重复
//去重前先排序
sort(nums.begin(), nums.end());
backtracking(nums, 0, used);
return result;
}
};
- 通过set容器去重
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums, int startindex)
{
result.push_back(path);
unordered_set<int> uset;
for(int i=startindex; i<nums.size(); i++)
{
//去重 使用find查找nums[i],find返回的是迭代器,元素所在位置
//如果不等于结束迭代器,说明在uset找到了nums[i]这个元素,相同元素跳过
if(uset.find(nums[i]) != uset.end()) continue;
uset.insert(nums[i]);//保存元素,标记
path.push_back(nums[i]);
backtracking(nums, i+1);
path.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
path.clear();
result.clear();
//去重前先排序
sort(nums.begin(), nums.end());
backtracking(nums, 0);
return result;
}
};
491.递增子序列

这道题是90.子集II的变形,注意与90.子集II的区别,递归终止条件和去重逻辑的变化
在90.子集II中,是通过先排序再加一个标记数组来去重的。但这道题自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了,所以不能使用之前的去重逻辑。
三要素及思路
先写逻辑,再确定递归函数参数:
path, 一维数组,保存符合条件的单个子集,全局变量
result,二维数组,存放子集集合,全局变量
nums,题目给的数组
startindex,下一层for循环搜索的起始位置,递归的起始位置,不能重复选取
终止条件:
- 和之前的子集问题一样,遍历整棵树,找所有节点,可以不需要终止条件,startIndex每次都会加1,并不会无限递归
- 但题目要求递增子序列至少有两个元素,相当于子集大小至少为2,
path.size() > 1,此时要保存结果。而非90.子集II中直接保存子集 - 因为要遍历整棵树,找到所有节点,不需要return,
单层搜索: 先去重,再标记元素、保存子集、递归、回溯,递归不重复选取元素,不排序
去重方式及去重优化
根据题目的意思,不能先排序再去重,也就说不可以使用 starindex条件控制去重 和 bool型标记数组去重。不排序的话,只能使用set来去重
去重
- 也是对同一父节点下本层的去重,区分树枝去重和树层去重
- set只记录本层元素是否重复使用,新的一层uset都会重新定义,相当于把上一层的记录清空。使用find查找,可以加快查找重复元素的速度,set是不允许存储相同元素的
- 去重时,要剔除两种情况,
- 一是同一树层的相同元素,
uset.find(nums[i-1])!=uset.end() - 二是树枝上,即下一层中元素不符合递增要求的元素,
!path.empty() && nums[i]
- 一是同一树层的相同元素,
去重优化-数组做哈希
题目中说数值范围[-100,100],可以用数组来做哈希。程序运行时,unordered_set 需要不停地insert,所以使用数组做哈希表,把key通过hash function映射为唯一的哈希值。
数组,set,map都可以做哈希表,而且数组能实现的,map和set也可以。但如果数值范围小的话,可以优先使用数组

代码
- 去重-set
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums, int startindex)
{
//终止条件 遍历整棵树不需要返回,且递增子序列中至少有两个元素时就要保存结果
if(path.size() > 1) result.push_back(path);//子集大小>1 至少有两个元素
//单层搜索
unordered_set<int> uset;//记录本层使用过的元素
for(int i=startindex; i<nums.size(); i++)
{
//去重 nums[i]
//nums[i]
//uset.find(nums[i])!=uset.end(),相当于找到相同元素
if((!path.empty() && nums[i]<path.back()) || uset.find(nums[i])!=uset.end()) continue;
uset.insert(nums[i]);
path.push_back(nums[i]);
backtracking(nums, i+1);
path.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
path.clear();
result.clear();
backtracking(nums, 0);
return result;
}
};
- 去重-数组做哈希表映射
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums, int startindex)
{
//终止条件 遍历整棵树不需要返回,且递增子序列中至少有两个元素时就要保存结果
if(path.size() > 1) result.push_back(path);//子集大小>1 至少有两个元素
//单层搜索
int uset[201] = {0};//哈希表,默认值是0,题目说数值范围[-100, 100]
for(int i=startindex; i<nums.size(); i++)
{
//去重 nums[i]
//题目的数值范围[-100, 100],数组实际范围是[0, 200] 因此需要nums[i]+100
if((!path.empty() && nums[i]<path.back()) || uset[nums[i]+100]==1) continue;
uset[nums[i]+100] = 1;//标记当前元素
path.push_back(nums[i]);
backtracking(nums, i+1);
path.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
path.clear();
result.clear();
backtracking(nums, 0);
return result;
}
};
总结
1. 切割问题
-
切割问题可以抽象为组合问题
-
如何模拟那些切割线
-
切割问题中递归如何终止
-
在递归循环中如何截取子串
-
如何判断回文
-
如何添加其他字符
-
验证区间合法性
-
- 分割回文串:
- 两种判断回文的方式
- 前后双指针、动态规划获取二维布尔矩阵
- 切割过的地方不能重复切割所以递归函数需要传入i + 1
-
- 复原IP地址: 操作字符串添加逗号作为分隔符,并验证区间的合法性
2. 子集问题
-
- 子集:子集问题和组合问题、分割问题的区别是,子集是收集树形结构中树的所有节点的结果;而组合和分割问题是收集树形结构中叶子节点的结果
-
- 子集Ⅱ:
- 着重理解树层去重和树枝去重
- 三种去重方式,startindex去重、bool型标记数组去重、set容器去重。注意去重前先排序
-
- 递增子序列
- 不同于90. 子集Ⅱ,注意递归终止条件和去重逻辑的变化,需要子集元素个数来控制递归结束;去重时不能对原数组排序
- 不能排序,只能使用set标记元素去重,set只记录本层元素,每次递归都要清空
- 去重优化,使用数组/map/set做哈希映射,如果数值范围小的话,优先考虑数组实现哈希表