《动手学深度学习》-57长短期记忆网络LSTM

沐神版《动手学深度学习》学习笔记，记录学习过程，详细的内容请大家购买书籍查阅。

b站视频链接
开源教程链接

长短期记忆网络（LSTM）

长期以来，隐变量模型存在长期信息保存和短期输入缺失的问题。解决这一问题的最早方法之一是长短期记忆网络。

长短期记忆网络的设计灵感来自于计算机的逻辑门。

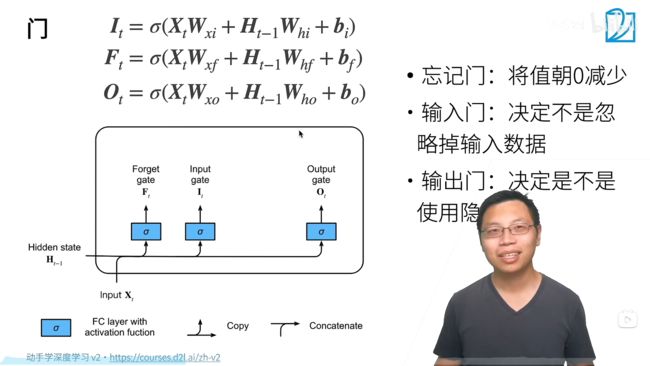
门控记忆元：
遗忘门：将值向0减少
输入门：决定是不是忽略掉输入数据
输出门：决定是不是使用隐状态

由3个带有$sigmoid$激活函数的全连接层处理：

候选记忆单元，与上面描述的3个门类似，但使用tanh函数作为激活函数，函数值范围为（-1，1）：

记忆单元：输入门$I_t$控制采用多少来自${\tilde{C}}_t$的新数据，而遗忘门$F_i$控制保留多少过去的记忆元$C_{t-1}$的内容。

如果遗忘门始终为1且输入门始终为0，则过去的记忆元$C_{t-1}$将随时间被保存并传递到当前时间步。引入这种设计是为了缓减梯度消失问题，并更好地捕获序列中的长距离依赖关系。

最后定义隐状态$H_t$的计算，这也是输出门发挥作用的地方。在长短期记忆网络中，它仅仅是记忆元的tanh的门控版本。这就确保了$H_t$的值始终在区间（-1，1）内。

只要输出门接近1，我们就能有效地将所有记忆信息传递给预测部分，而对于输出门接近0，我们只保留记忆元内的所有信息，而不需要更新隐状态。

有些文献认为记忆元是隐状态的一种特殊类型，它们与隐状态具有相同的形状，其设计目的是用于记录附加的信息。

总结

长短期记忆网络是典型的具有重要状态控制的隐变量自回归模型。然后由于序列的长距离依赖性，训练长短期记忆网络和其他序列模型（如门控循环单元）的成本是相当高的。Transformer是其高级替代模型。

LSTM可以缓解梯度爆炸和梯度消失。

只有隐状态会传递到输出层（Y），而记忆元完全属于内部信息。

动手学

长短期记忆网络-LSTM

import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

def get_lstm_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01

    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    W_xi, W_hi, b_i = three()  # 输入门参数
    W_xf, W_hf, b_f = three()  # 遗忘门参数
    W_xo, W_ho, b_o = three()  # 输出门参数
    W_xc, W_hc, b_c = three()  # 候选记忆元参数

    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    
    # 附加梯度
    params = [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc,
              b_c, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    
    return params

# H 和 C 的初始化
def init_lstm_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device),
            torch.zeros((batch_size, num_hiddens), device=device))

def lstm(inputs, state, params):

    [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
     W_hq, b_q] = params
    (H, C) = state
    
    outputs = []
    for X in inputs:

        I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i) # 输入门
        F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f) # 遗忘门
        O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o) # 输出门
        
        C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c) # 候选记忆单元
        
        C = F * C + I * C_tilda # 记忆元
        
        H = O * torch.tanh(C) # 隐状态

        Y = (H @ W_hq) + b_q # 输出
        outputs.append(Y)
        
    return torch.cat(outputs, dim=0), (H, C)

vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_lstm_params,
                            init_lstm_state, lstm)
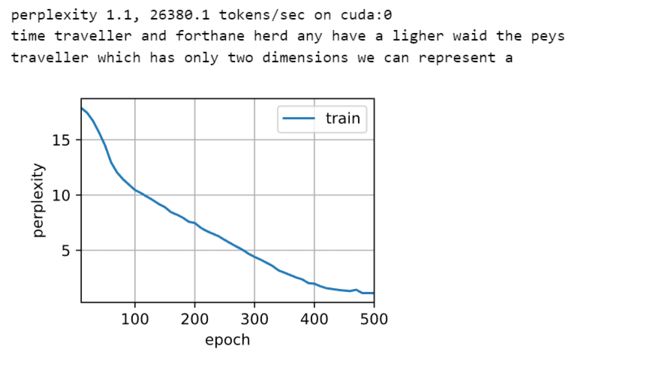
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

简洁实现

num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)