二叉树(上)
“路虽远,行则将至”
❤️主页:小赛毛
目录
1.树概念及结构
1.1树的概念
1.2 树的相关概念
1.3 树的表示(树的存储)
2.二叉树概念及结构
2.1概念
2.2现实中的二叉树
2.3 特殊的二叉树:
2.4 二叉树的性质
3.二叉树的顺序结构及实现
3.1 二叉树的顺序结构
3.2 堆的概念及结构
3.3 堆的实现
3.2.1 堆向下调整算法
3.2.2堆的创建
前言:
在进入今天的正题之前,我们先来回顾一下我们已经学过的知识:
顺序的本质是什么呢?数组
但是呢,顺序表在这里是有一些缺陷的:
1.中间或者头部插入删除数据要挪动数据,效率低
2.空间不够,只能扩容。扩容有消耗
3.倍数扩容,用不完,存在空间浪费
当然,有利有弊,优点:
1.下标随机访问。排序 二分查找适合
2.CPU高速缓存命中率比较高
在我们学完顺序表之后呢,我们当时顺序就学了链表:
在这里呢,我们要请出链表的典型代表——带头结点的双向循环链表 同志来参加。
优点:
1.任意位置插入删除效率高
2.按需申请释放,不存在扩容
缺点:
1.不能下标随机访问
2.CPU高速缓存命中率低
1.树概念及结构
1.1树的概念
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 树的相关概念
- 节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度;如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;(并查集里面就是多棵树)
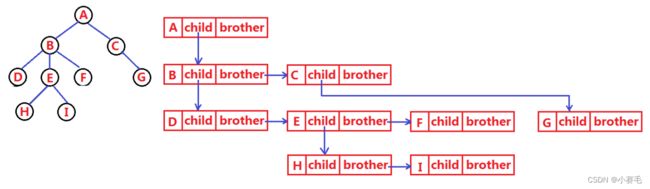
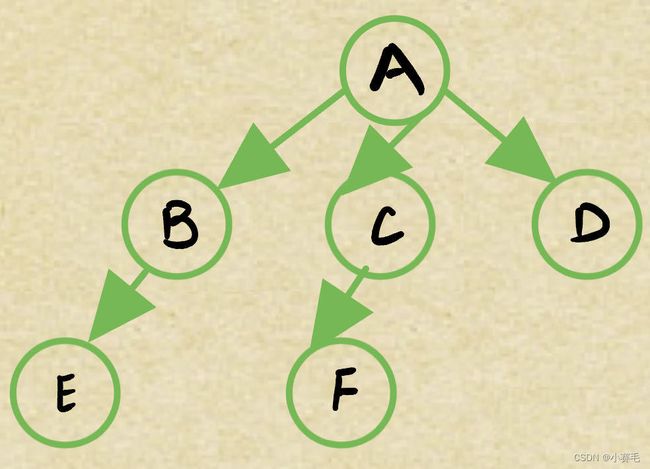
1.3 树的表示(树的存储)
struct TreeNode
{
int val;
struct TreeNode* firstchild;//第一个孩子节点
struct TreeNode* nextbroyher;//指向其下一个兄弟节点
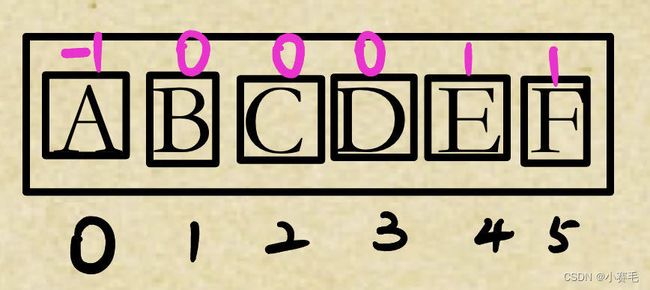
}双亲表示法(只存储父亲的下标或指针):
在很多地方,双亲表示法一般就是用数组的方式直接玩
这个地方就可以很容易判断出来有几棵树,有几个兄弟。
于是否,两个节点在不在同一棵树,如何判断?
找根,根相同就在同一棵树
其实呢,在实际生活中,我们用的最多的实际上是二叉树
2.二叉树概念及结构
2.1概念
2.2现实中的二叉树
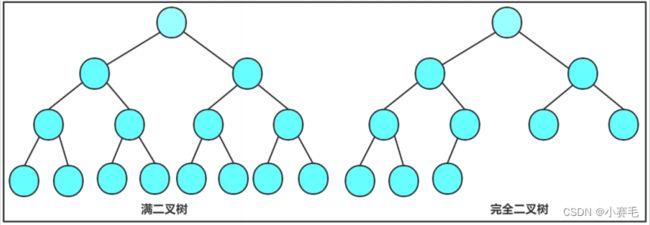
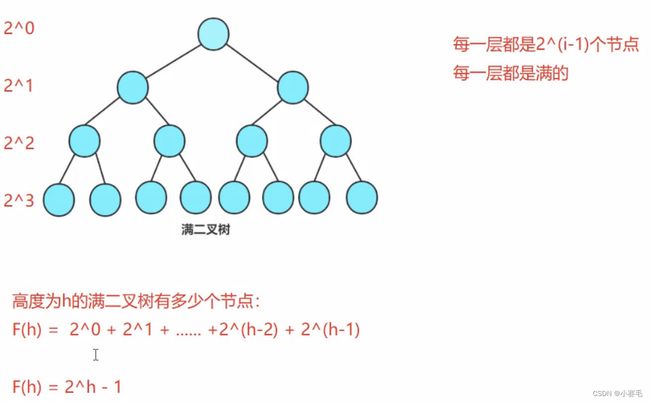
2.3 特殊的二叉树:
2.4 二叉树的性质
3.二叉树的顺序结构及实现
3.1 二叉树的顺序结构
parent = (child-1) / 2
任意位置通过下标可以找父亲或者孩子
那如果不是满二叉树或者完全二叉树的话,还适合这个规律吗?显然不可以
那我们这里可以进行总结:
满二叉树 或者 完全二叉树适合用数组存储
3.2 堆的概念及结构
3.3 堆的实现
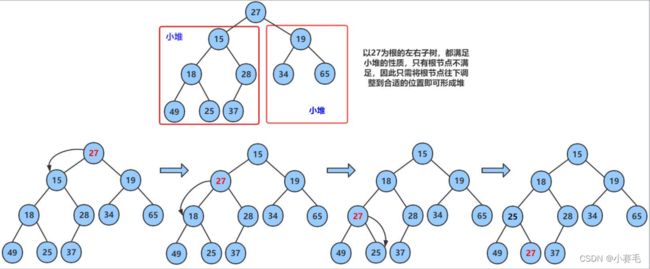
3.2.1 堆向下调整算法
我们在这里先来说明一下:
栈:线性表,后进先出
堆:非线性表,完全二叉树
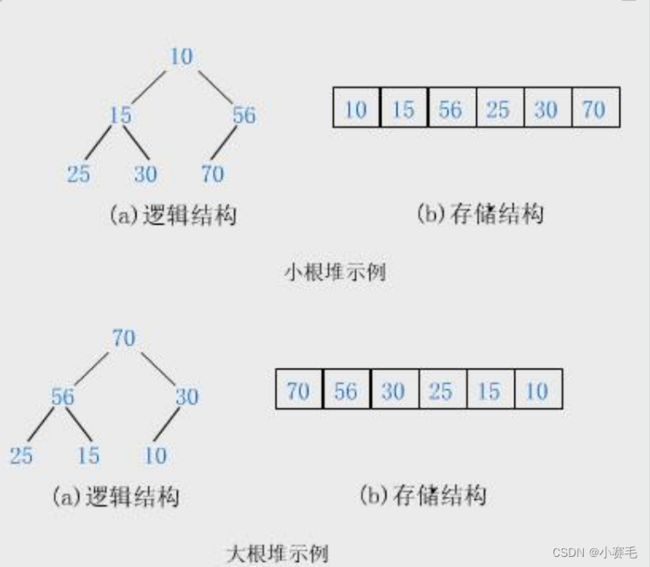
小堆:树中任意一个父亲都 ≤ 孩子
大堆:树中任意一个父亲都 ≥ 孩子
intarray[] = {27,15,19,18,28,34,65,49,25,37};底层:
- 物理结构:数组
- 逻辑结构:完全二叉树
小堆,底层数组是否升序呢?不一定
小堆的根是整棵树的最小值
3.2.2堆的创建
inta[] = {1,5,3,8,7,6};