异或运算 XOR ⊕ 教程
目录
1 含义
2 运算定律
3 应用
3.1 简化计算
3.2 交换值
3.3 加密
3.4 数据备份
4 一道面试题
5 python的异或
大家比较熟悉的逻辑运算,主要是"与运算"(AND)和"或运算"(OR),还有一种"异或运算"(XOR),也非常重要。
本文介绍异或运算的含义和应用。
1 含义
XOR 是 exclusive OR 的缩写。英语的 exclusive 意思是"专有的,独有的",可以理解为 XOR 是更单纯的 OR 运算。异或的数学符号为“⊕”,计算机符号为“eor”。
我们知道,OR 运算的运算子有两种情况,计算结果为true。
(1)一个为 true,另一个为 false;
(2)两个都为 true。
上面两种情况,有时候需要明确区分,所以引入了 XOR。
XOR 排除了第二种情况,只有第一种情况(一个运算子为true,另一个为false)才会返回 true,所以可以看成是更单纯的 OR 运算。也就是说, XOR 主要用来判断两个值是否不同。
其运算法则为:
a⊕b = (¬a ∧ b) ∨ (a ∧¬b)
如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0。异或也叫半加运算,其运算法则相当于不带进位的二进制加法:二进制下用1表示真,0表示假,则异或的运算法则为:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0(同为0,异为1),这些法则与加法是相同的,只是不带进位,所以异或常被认作不进位加法。
XOR 一般使用插入符号(caret)^表示。如果约定0 为 false,1 为 true,那么 XOR 的运算真值表如下。
0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 02 运算定律
XOR 运算有以下的运算定律。由于非常简单,这里就省略证明了。
(1)归零律:![]()
一个值与自身的运算,总是为 false。
x ^ x = 0(2)恒等律:![]()
一个值与 0 的运算,总是等于其本身。
x ^ 0 = x(3)交换律: ![]()
可交换性
x ^ y = y ^ x(4)结合律:![]()
结合性
x ^ (y ^ z) = (x ^ y) ^ z(5)自反:![]()
(6)d = a ⊕ b ⊕ c 可以推出 a = d ⊕ b ⊕ c.
(7)若x是二进制数0101,y是二进制数1011;
则 x ⊕ y=1110。
只有在两个比较的位不同时其结果是1,否则结果为0
即“两个输入相同时为0,不同则为1”。
3 应用
根据上面的这些运算定律,可以得到异或运算的很多重要应用。
3.1 简化计算
多个值的异或运算,可以根据运算定律进行简化。
a ^ b ^ c ^ a ^ b
= a ^ a ^ b ^ b ^ c
= 0 ^ 0 ^ c
= c3.2 交换值
两个变量连续进行三次异或运算,可以互相交换值。
假设两个变量是 x和 y,各自的值是 a和 b。下面就是 x和 y进行三次异或运算,注释部分是每次运算后两个变量x和 y的值。
x = x ^ y // (a ^ b, b)
y = x ^ y // (a ^ b, a ^ b ^ b) => (a ^ b, a)
x = x ^ y // (a ^ b ^ a, a) => (b, a)这是两个变量交换值的最快方法,不需要任何额外的空间。
3.3 加密
异或运算可以用于加密。
第一步,明文(text)与密钥(key)进行异或运算,可以得到密文(cipherText)。
text ^ key = cipherText第二步,密文与密钥再次进行异或运算,就可以还原成明文。
cipherText ^ key = text原理很简单,如果明文是 x,密钥是 y,那么 x 连续与 y 进行两次异或运算,得到自身。
(x ^ y) ^ y
= x ^ (y ^ y)
= x ^ 0
= x3.4 数据备份
异或运算可以用于数据备份。
文件 x 和文件 y 进行异或运算,产生一个备份文件 z。
x ^ y = z以后,无论是文件 x 或文件 y 损坏,只要不是两个原始文件同时损坏,就能根据另一个文件和备份文件,进行还原。
x ^ z
= x ^ (x ^ y)
= (x ^ x) ^ y
= 0 ^ y
= y上面的例子是 y 损坏,x 和 z 进行异或运算,就能得到 y。
4 一道面试题
一些面试的算法题,也能使用异或运算快速求解。
请看下面这道题。
一个数组包含 n-1 个成员,这些成员是 1 到 n 之间的整数,且没有重复,请找出缺少的那个数字。最快的解答方法,就是把所有数组成员(A[0] 一直到 A[n-2])与 1 到 n 的整数全部放在一起,进行异或运算。
A[0] ^ A[1] ^ ... ^ A[n-2] ^ 1 ^ 2 ^ ... ^ n上面这个式子中,每个数组成员都会出现两次,相同的值进行异或运算就会得到 0。只有缺少的那个数字出现一次,所以最后得到的就是这个值。
你可能想到了,加法也可以解这道题。
1 + 2 + ... + n - A[0] - A[1] - ... - A[n-2]但是,加法的速度没有异或运算快,而且需要额外的空间。如果数字比较大,还有溢出的可能。
下面是一道类似的题目,大家可以作为练习。(快慢指针思想?)
一个数组包含 n+1 个成员,这些成员是 1 到 n 之间的整数。只有一个成员出现了两次,其他成员都只出现一次,请找出重复出现的那个数字。5 python的异或
让我们先来看两段对话:
技术员:这个水坝系统的设计思路为按下紧急按钮或者水位高于危险水位时,系统发出警报
提问者:这个“或者”是 排他的么?
技术员:什么意思?
提问者:就是说,按下紧急按钮并且水位高于危险水位时,会发出警报么?
技术员:当然会啦!!!
****************************************
发言者:他现在在北京或者上海
提问者:这个“或者”是排他的么?
发言者:什么意思?
提问者:就是说,他有可能在北京的同时在上海么?
发言者:这怎么可能呢??????
显然,这两段对话中的“或者”代表的意思并不相同。
- 第一个“或者”并不排他,也就是普通或者 在Python中用逻辑运算符 or 表示
- 第二个“或者”是排他的,也就是我们说的异或(xor)在Python中则用 ^ 表示
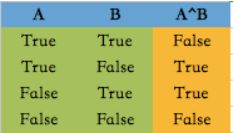
让我们用真值表来看一下异或的运算逻辑:
也就是说:
“A B有一个为真 但不同时为真” 的运算称作异或。
如果我们将布尔值之间的异或换成数字之间的异或会发生什么?
0 ^ 0
0 ^ 1
1 ^ 0
1 ^ 1
>>>0
1
1
0结果告诉我们 数字相同异或值为0 数字不相同异或值为1
让我们再试试0,1除外的数字:
5 ^ 3
>>>6为什么答案会是6,不应该是1么??这背后发生了什么?
异或是基于二进制基础上按位异或的结果 5 ^ 3 的过程 其实是将5和3分别转换为二进制:
5 = 0101(b)
3 = 0011(b)
按位异或:
- 0^0 ->0
- 1^0 ->1
- 0^1 ->1
- 1^1 ->0
排起来就是0110(b) 转换为十进制:6
注:可以用bin计算一个数字的二进制值。
bin(2)
# '0b10'
bin(10)
# '0b1010'具体的用法:
本来我们想把一个flag在True和False之间转换 需要这么写:
flag = True
if something:
flag = False if flag else True而用异或直接这么写就可以了:
flag = False
if something:
flag ^= True异或运算 XOR 教程:http://www.ruanyifeng.com/blog/2021/01/_xor.html
That XOR Trick:https://florian.github.io/xor-trick/