【C语言】找单身狗问题
一.找单身狗问题初阶
1.问题描述
一个数组中只有一个数字是出现一次,其他所有数字都出现了两次.编写一个函数,找出这个只出现一次的数字.
例如:
有数组的元素是:1,2,3,4,5,1,2,3,4
只有5出现了一次,要找出5.
2.解题思路
常规思路:
在常规思路中,我们首先想到的肯定是使用两层循环嵌套的方式遍历整个数组,
如果在遍历的过程中,有数字找到了和它相同的数字,那么终止循环,换下一个数字遍历,
直到找出那个遍历完整个数组都没有找到与它相同的数为止.
由该思路得出的代码如下:
#include
int Find_single_dog(int* str, int sz)
{
int i = 0;
int j = 0;
for (i = 0; i < sz; i++)
{
int num = str[i];
for (j = 0; j < sz; j++)
{
if (i == j)
{
continue;//当遍历到它自身时,该次循环无效,我们直接跳出本次循环
}
if (str[i] == str[j])
{
break;//当遍历到和它相同的数时,证明他不是"单身狗",终止循环,寻找下一个数
}
}
if (j == sz)
{
return str[i];//当遍历完整个数组时还没有找到和它相等的数,则该数字即为"单身狗"
}
}
}
int main()
{
int arr[] = { 1,2,3,4,5,1,2,3,4 };
int sz = sizeof(arr) / sizeof(arr[0]);
int single_dog=Find_single_dog(arr, sz);
printf("%d", single_dog);
return 0;
} 代码运行结果:
虽然该思路有效的完成了我们的要求,但该代码的循环次数是非常多的,
设数组一共有n个元素,则循环次数就几乎等于:n^n.
因此这种方法的时间复杂度非常高,程序的运行效率很低.
进阶思路:
在C语言中有一个异或(^)逻辑运算符,我们可以利用它的自反性质来找出"单身狗".
如果有对异或(^)还不是很了解的朋友可以先移步这篇博客,了解一下关于异或的一些性质,有助于理解后面的操作.【C语言】异或(^)操作符详解
先将文章里面的部分内容截出方便我们后续使用:
异或的运算法则(部分):
接下来我们画图来解释一下异或操作的步骤:
可以发现,凡是出现过两次的数字,两两异或后都变成了0,而唯一的只出现了一次的数字,与0异或的结果仍然是它本身,这说明整个数组相异或的结果恰好就是我们要找的"单身狗".
理解了进阶的思路后,代码的编写就很容易了,如下:
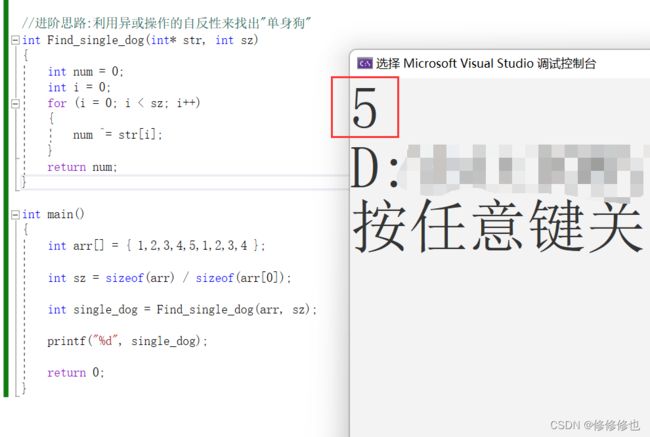
//进阶思路:利用异或操作的自反性来找出"单身狗"
int Find_single_dog(int* str, int sz)
{
int num = 0;
int i = 0;
for (i = 0; i < sz; i++)
{
num ^= str[i];
}
return num;
}
int main()
{
int arr[] = { 1,2,3,4,5,1,2,3,4 };
int sz = sizeof(arr) / sizeof(arr[0]);
int single_dog = Find_single_dog(arr, sz);
printf("%d", single_dog);
return 0;
}代码运行测试:
可以看到,该代码同样成功得到了我们想要的结果,并且当数组中有n个元素时,代码循环的次数为n,比常规思路中的n^n的时间复杂度简化了不少,运行效率也非常高.
二.找单身狗问题进阶
1.问题描述
一个数组中只有两个数字是出现一次,其他所有数字都出现了两次.编写一个函数,找出这个两个只出现一次的数字.
例如:
有数组的元素是:1,2,3,4,5,1,2,3,4,6
只有5和6出现了一次,要找出5和6.
2.解题思路
常规思路:
在常规思路中,我们同样是使用两层循环嵌套的方式遍历整个数组,
如果在遍历的过程中,有数字找到了和它相同的数字,那么终止循环,换下一个数字遍历,
直到找出遍历完整个数组都没有找到与它相同的数,将这个数打印/存储,
再继续换下一个数遍历,寻找下一个"单身狗".
由该思路得出的代码如下:
void Find_single_dog(int* str, int sz)
{
int i = 0;
int j = 0;
for (i = 0; i < sz; i++)
{
int num = str[i];
for (j = 0; j < sz; j++)
{
if (i == j)
continue;
if (str[i] == str[j])
break;
}
if (j == sz)
printf("%d ", str[i]);
}
}
int main()
{
int arr[] = { 1,2,3,4,5,1,2,3,4,6};
int sz = sizeof(arr) / sizeof(arr[0]);
Find_single_dog(arr, sz);
return 0;
}运行结果:
可以发现,在进阶问题中,常规思路和初阶问题的常规思路复杂度几乎没有区别,效率同样很低.
进阶思路:
先来观察数组:
int arr[]={1,2,3,4,5,1,2,3,4,6};我们把这几个数组元素摘出来,便于观察:
接下来就是要解决问题了,首先我们想到的是,能不能将这些元素分成两组,
当然最主要的还是将5和6这两个单身狗分开,并且保证每组剩余的数是成对出现的:
如:
1 1 3 3 5 (第一组)
2 2 4 4 6 (第二组)
这样的话,我们就可以分别对第一组和第二组使用刚才初阶问题中的全部相异或的方法来得到5和6.
那么分组时,最重要的就是需要找出两个单身狗(5和6)的区别:
在本例中,显而易见,5是奇数,6是偶数,
也就是说,5的二进制位最低位一定为1,而6的二进制位最低位一定为0.
那么我们就可以将二进制位的最低位是否为1作为分组的依据,进而将数组的全部元素按该条件进行分组就可以达到我们的目的了.
但这样做的话还有一个问题,那就是当单身狗是6和8的时候呢?它们的二进制末位都是0时,该如何将它俩区分呢?
这时我们可以尝试将两个单身狗异或一下,就能找到其中的规律.
如:
6的二进制表示为 0 1 1 0
8的二进制表示为 1 0 0 0 根据异或运算的规则:相同取0,相异取1
它们异或的结果为 1 1 1 0
可以发现,除了末位,6和8异或后倒数第二位,倒数第三位和倒数第四位的结果都为1,说明这三位上它们的二进制都不相同.
那么我们就可以用这三位的任意一位来作为分组的依据,就可以将6和8分到不同的组中了.
因此,我们在最开始的时候将数组中的所有元素相异或,得到的其实就是两个单身狗相异或的结果,
然后将该结果的二进制位从最低位开始检索,直到找到为"1"的那一位,记录下这一位,并以此作为分组的依据,将数组元素分为两组后分别相异或,得到的两个结果就是要找的两个单身狗.
由该思路所得代码如下:
//进阶思路
void Find_single_dog(int* str, int sz)
{
int i = 0;
int num = 0;
for (i = 0; i < sz; i++)
num ^= str[i];
//计算num的哪一位是1,并记录下来
int pos = 0;
for (i = 0; i < 32; i++)
{
if (((num >> i) & 1) == 1)
{
pos = i;
break;
}
}
int single_dog1 = 0;
int single_dog2 = 0;
for (i = 0; i < sz; i++)
{
if (((str[i] >> pos) & 1) == 1)//以第pos位是否为1为条件,将元素分为两组分别异或得出结果
single_dog1 ^= str[i];
else
single_dog2 ^= str[i];
}
printf("%d %d\n",single_dog1,single_dog2);
}
int main()
{
int arr[] = { 1,2,3,4,5,1,2,3,4,6 };
int sz = sizeof(arr) / sizeof(arr[0]);
Find_single_dog(arr, sz);
return 0;
}运行结果:
当数组的元素为n时,可得进阶的时间复杂度约等为:2n+32.相比常规思路的n^n效率高了不少.
因此在后续的类似找"单身狗"的问题中,希望大家可以多多使用异或的方式来提升查找的效率.