动态规划基础模型学习
动态规划学习
递推算法
70.爬楼梯
class Solution {
public int climbStairs(int n) {
//java数组实现
int[] arr=new int[45];
arr[0]=1;
arr[1]=2;
for(int i=2;i面试题08.06 汉诺塔问题
class Solution {
public void hanota(List A, List B, List C) {
move(A.size(),A,B,C);
}
public void move(int num,List start, List mid, List end){
//递归结束条件
if(num==1){
end.add(start.remove(start.size()-1));
return;
}
move(num-1,start,end,mid);
end.add(start.remove(start.size()-1));
move(num-1,mid,start,end);
}
}
96.不同的二叉搜索树
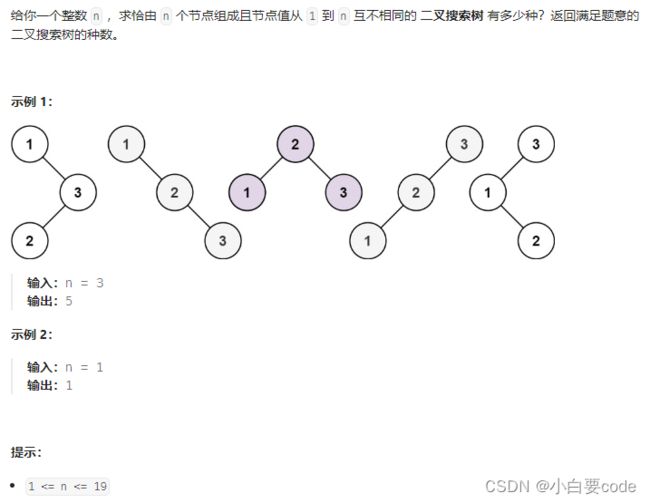
思路:假设n个节点存在二叉排序树的个数是G(n),1为根节点,2为根节点,…,n为根节点,当1为根节点时,其左子树节点个数为0,右子树节点个数为n-1,同理当2为根节点时,其左子树节点个数为1,右子树节点为n-2,所以可得G(n) = G(0)G(n-1)+G(1)(n-2)+…+G(n-1)*G(0)
class Solution {
public int numTrees(int n) {
int[] arr=new int[n+1];
arr[0]=1;
arr[1]=1;
for(int i=2;i<=n;i++){
for(int j=0;j62.不同路径
class Solution {
public int uniquePaths(int m, int n) {
//f(m,n)=f(m-1,n)+f(m,n-1)
int[][] f=new int[m][n];
for(int i=0;i数字三角形
class Solution {
public int minimumTotal(List> triangle) {
int n=triangle.size();
int[][]f=new int[n][n];
f[0][0]=triangle.get(0).get(0);
for(int i=1;i 一维动态规划
198.打家劫舍
class Solution {
public int rob(int[] nums) {
if(nums.length==1) return nums[0];
int[] f=new int[nums.length];
f[0]=nums[0];
f[1]=nums[1];
for(int i=2;im){
m=arr[i];
}
}
return m;
}
}
213.打家劫舍 II
//分两次动态规划
class Solution {
public int rob(int[] nums) {
if(nums.length==1) return nums[0];
if(nums.length==2) return Math.max(nums[0],nums[1]);
int[] f=new int[nums.length-1];
int[] g=new int[nums.length-1];
f[0]=nums[0];
f[1]=nums[1];
g[0]=nums[1];
g[1]=nums[2];
for(int i=2;im){
m=arr[i];
}
}
return m;
}
}
873.最长斐波拉契子序列的长度
class Solution {
public int lenLongestFibSubseq(int[] arr) {
Map map=new HashMap<>();
//初始化map
map.put(arr[0],0);
map.put(arr[1],1);
int max=0;
int[][] dp=new int[arr.length][arr.length];
dp[1][0]=2;
for(int i=2;i=0;k--){
dp[i][k]=2;
if (arr[k]<=arr[i]/2) continue;
if(map.getOrDefault(arr[i]-arr[k],arr.length+1) 二维动态规划
174.地下城游戏
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
int m = dungeon.length;
int n = dungeon[0].length;
// 创建一个二维DP数组来存储所需的最小生命值
int[][] dp = new int[m][n];
// 从右下角开始
dp[m - 1][n - 1] = Math.max(1, 1 - dungeon[m - 1][n - 1]);
// 填充最后一行和最后一列
// 在最后一行时,只能向右;在最后一列时,只能向左
for (int i = m - 2; i >= 0; i--) {
dp[i][n - 1] = Math.max(dp[i + 1][n - 1] - dungeon[i][n - 1], 1);
}
for (int j = n - 2; j >= 0; j--) {
dp[m - 1][j] = Math.max(dp[m - 1][j + 1] - dungeon[m - 1][j], 1);
}
// 从右下角向左上角填充DP数组
for (int i = m - 2; i >= 0; i--) {
for (int j = n - 2; j >= 0; j--) {
int minRequired = Math.min(dp[i + 1][j], dp[i][j + 1]);
dp[i][j] = Math.max(minRequired - dungeon[i][j], 1);
}
}
return dp[0][0];
}
}
最长单调子序列
300.最长递增子序列
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp=new int[nums.length];
//初始化
Arrays.fill(dp,1);
int max=1;
for(int i=1;inums[j]){
dp[i]=Math.max(dp[i],dp[j]+1);
}
}
max=Math.max(max,dp[i]);
}
//System.out.print(Arrays.toString(dp));
return max;
}
}
最长公共子序列
1143.最长公共子序列
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int n=text1.length();
int m=text2.length();
int[][] dp=new int[n][m];
for(int i=0;i72.编辑距离
class Solution {
public int minDistance(String word1, String word2) {
int n=word1.length();
int m=word2.length();
int[][] dp=new int[n+1][m+1];
//初始化,第一行和第一列为空字符串,全为删除操作
for(int i=0;i<=n;i++){
dp[i][0]=i;
}
for(int j=0;j<=m;j++){
dp[0][j]=j;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1];
}
else{
int temp=Math.min(dp[i-1][j],dp[i][j-1]);
dp[i][j]=Math.min(temp,dp[i-1][j-1])+1;
}
}
}
// for(int i=0;i<=n;i++){
// for(int j=0;j<=m;j++){
// System.out.print(dp[i][j]);
// }
// }
return dp[n][m];
}
}
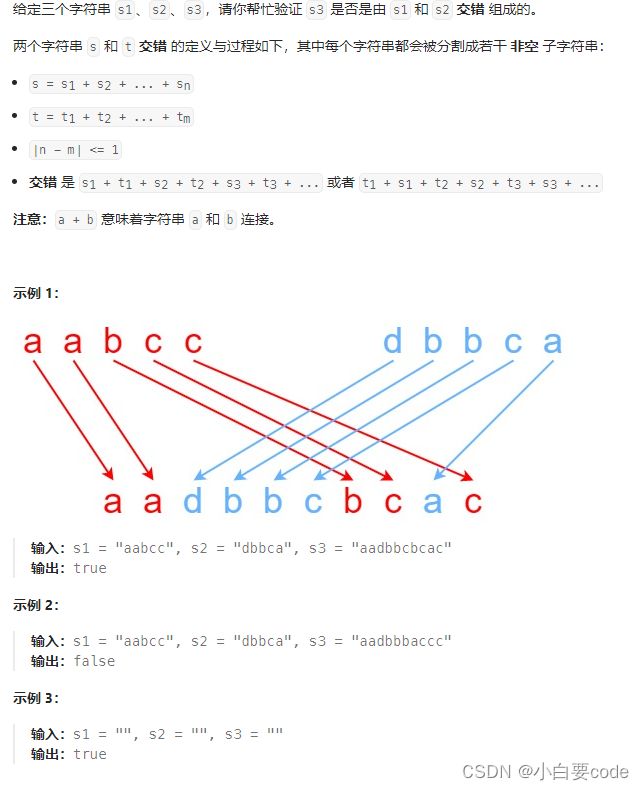
97.交错字符串
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
if(s1.length()+s2.length()!=s3.length()){
return false;
}
int n=s1.length();
int m=s2.length();
boolean[][] dp=new boolean [n+1][m+1];
dp[0][0]=true;//都为空的情况
//默认false
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(i>0)
if(s3.charAt(i+j-1)==s1.charAt(i-1)){
dp[i][j]=dp[i][j]||dp[i-1][j];
}
if(j>0)
if(s3.charAt(i+j-1)==s2.charAt(j-1)){
dp[i][j]=dp[i][j]||dp[i][j-1];
}
}
}
// for(int i=0;i<=n;i++){
// for(int j=0;j<=m;j++){
// System.out.println(dp[i][j]);
// }
// }
return dp[n][m];
}
}
最长连续子段和
53.最大子数组和
public class Solution {
public int maxSubArray(int[] nums) {
int len = nums.length;
// dp[i] 表示:以 nums[i] 结尾的连续子数组的最大和
int[] dp = new int[len];
dp[0] = nums[0];
for (int i = 1; i < len; i++) {
if (dp[i - 1] > 0) {
dp[i] = dp[i - 1] + nums[i];
} else {
dp[i] = nums[i];
}
}
int res = dp[0];
for (int i = 1; i < len; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
}
918.环形子数组的最大和
class Solution {
public int maxSubarraySumCircular(int[] nums) {
int sum=nums[0];
int len=nums.length;
int[] dp=new int[len];
int max=nums[0];
dp[0]=nums[0];
//1.子数组最大和
//dp[i]表示到i位置的最大子数组和
for(int i=1;imax) max=dp[i];
sum+=nums[i];
}
//2.包含环(第一个和最后一个),求中间最小子数组和
//dp[j]表示到j位置的最小子数组和
int min=0;
for(int j=1;j 面试题17.24最大子矩阵
class Solution {
int a=0;
int b=0;
public int[] getMaxMatrix(int[][] matrix) {
int n=matrix.length;
int m=matrix[0].length;
int dp[][]=new int[n][m];
int max=matrix[0][0];
int[] res=new int[4];
for(int i=0;imax){
max=matrix_max;
res[0]=i;
res[1]=a;
res[2]=k;
res[3]=b;
}
}
}
return res;
}
public int maxSubArray(int[] nums) {
int len = nums.length;
// dp[i] 表示:以 nums[i] 结尾的连续子数组的最大和
int[] dp = new int[len];
dp[0] = nums[0];
int max=dp[0];
a=0;
b=0;
for (int i = 1; i < len; i++) {
if (dp[i - 1] > 0) {
dp[i] = dp[i - 1] + nums[i];
} else {
dp[i] = nums[i];
}
if(dp[i]>max){
max=dp[i];
b=i;
for(int k=b;k>0;k--){
if(dp[k-1]<0) {
a=k;
break;
}
}
}
}
return max;
}
}