成语接龙 | c++ | 建图和BFS
写在最开始:这题能够做出来基本全靠一位学长的经验分享,详见这一篇
--> 【第二十一题】成语接龙(北理工/北京理工大学/程序设计方法与实践/小学期 )http://t.csdn.cn/fcTLy![]() http://t.csdn.cn/fcTLy本文可以算是对学长已发帖子的进一步梳理,主要是一些个人理解,欢迎补充。
http://t.csdn.cn/fcTLy本文可以算是对学长已发帖子的进一步梳理,主要是一些个人理解,欢迎补充。
这篇真的是小白向。当我上CSDN搜索“图的实现”,出来的结果往往是先梳理图的基本知识,然后立刻就毫无征兆地冒出来一堆莫名其妙的代码,不加任何解释,让我看着非常头大。所以这一篇既是我个人的笔记梳理,也算是帮助其他像我一样没有c++基础的“真”小白入门。
一、题目描述
Description
小张非常喜欢与朋友们玩成语接龙的游戏,但是作为“文化沙漠”的小张,成语的储备量有些不足。现在他的大脑中存储了 m 个成语,成语中的四个汉字都用一个 1e6 以内的正整数来表示。现在小张的同学为了考验他给出了他一个成语做开头和一个成语做结尾,如果小张能通过成语接龙的方式说到结尾的成语,他就能够成功完成游戏。他想知道最少能说几个成语能够成功完成游戏。Input
第一行一个数。
接下来行,每行4个 1e6 以内的正整数,表示一个成语。
下一行4个 1e6 以内的正整数,表示开始成语。
下一行4个 1e6 以内的正整数,表示结束成语。
保证开始成语和结束成语在小张的成语储备之中。
Output
一行一个整数,表示最少说几个成语能够完成游戏。如果无法完成输出-1。Notes
三个成语分别是(1,2,3,4)(4,5,6,7)(7,8,9,10)
测试输入 期待的输出 时间限制 内存限制 额外进程 测试用例 1 以文本方式显示
- 5↵
- 1 2 3 4↵
- 4 5 6 7↵
- 7 8 9 10↵
- 4 6 6 1↵
- 1 6 8 8↵
- 1 2 3 4↵
- 7 8 9 10↵
以文本方式显示
- 3↵
1秒 64M 0
二、个人笔记
1、queue和map的简单初始化
queue和map在c++中现成的数据结构,如果会的话可以直接调用,非常方便。
(1) queue
queue queue_name;
其中,type是数据类型,container是容器类型,queue_name是队列名称。container可以省略。
例如,要初始化一个存储int整型变量、名称为Q的队列:
queue Q; (2) map
map map_name; 其中,type1和type2是两个数据类型,map_name是map名称。
例如,要建一个int类型指向string类型、名为graph的图表:
map graph;
graph[0] = "abc";
//表示graph中,0指向“abc” 2、%*d和%.*d
scanf("%d %*d %d",&a,&b);
printf("a=%d b=%d\n",a,b);
printf("%*d",10,a);
printf("\n");
printf("%.*d",10,b);输入
10 20 30
输出
a=10 b=30
10(8个空格,一个10)
0000000030(8个0,一个10)
scanf和printf中的%*d是不一样的。
①scanf中的%*d,会在读入时占用一个数,且不存入变量。
而printf中的%*d,是用空格补齐输出。
②scanf中的%.*d,是非法的,会报错。
而printf中的%.*d,是用0来补齐输出。
3、queue库的简单操作
Q.push() 在队尾插入一个元素
Q.pop() 删除队列第一个元素
Q.size() 返回队列中元素个数
Q.empty() 如果队列空则返回true
Q.front() 返回队列中的第一个元素
Q.back() 返回队列中最后一个元素4、map库的简单操作
插入:graph.insert( pair (type1_data,type2_data) )
修改:直接修改 graph[0] = "aaa";
查找:graph.find(key);
删除:graph.erase(key);
清空:graph.clear();
第一个元素迭代器:graph.begin();
最后一个元素迭代器:graph.end();
当然,这题我只需要用到修改就足够了。
5、auto类型
用来简化变量的初始化,例如:
auto i = "Hello world!";
//相当于string i = "Hello world!";
for (auto i=0 ; i<10 ; i++) { }
//相当于for (int i=0 ; i<10 ; i++) { }对于基本的int、char、string、double、pair<>等没什么太大的优势,但是当我们需要用到比较复杂的变量时,auto比较方便。
6、两种基本搜索算法及其实现
就是很多教程,要么只讲原理不讲代码,要么代码太过高深,所以这里咱们还是尽量说清楚怎么实现。
(1)DFS(Depth-First-Search)
选择一条路径一直访问,否则回溯。
(Ⅰ)详细的原理解释
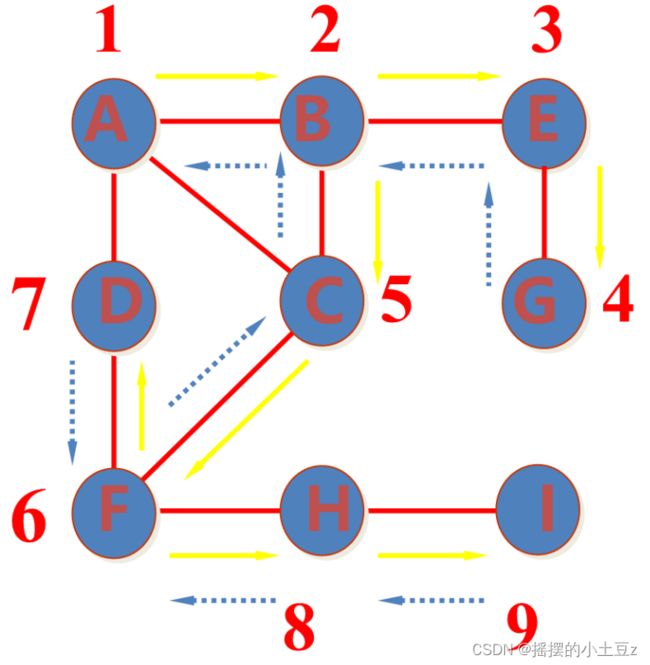
从A开始,先选择ABEG这一条路一直走到底。(这里每一个节点的分支选择是完全随机的)
走到底为G,于是回溯到上一步,为E。
但是E没有分支,于是继续回溯到上一步,为B。
发现B有分支BC,于是沿着BC这一条分支一直走到底。注意,一条分支下面可能还有多个分支,但是不要紧,我们完全是随机选择的,只要能走到底就行了。例如图中在节点F选择去了D,当然也可以去H,没有太大影响。
走到D之后,因为A已经去过了,所以已经走到了底。
于是回溯到上一步,为F,F有分支FH,于是顺着这一条路走到底,走到了I,至此,DFS结束。
依次经过点的顺序是ABEGCFDHI。
如果要把上面的过程转化成代码,需要注意的几个问题:
①走到底; ②回溯; ③访问过的要标记。
(Ⅱ)代码示例
【这块先鸽着】
(2)BFS(Breadth-First-Search)
(Ⅰ)详细的原理解释
定义队列q={}。
从1开始,将1加入队列,q={1}。
从队列中取出队首1,q={}。然后将和1相连的未访问元素加入q,q={2,3}。
从队列中取出队首2,q={3}。然后将和2相连的未访问元素加入q,q={3,4}。
从队列中取出队首3,q={4}。然后将和3相连的未访问元素加入q,q={4,5,7}。
从队列中取出队首4,q={5,7}。然后将和4相连的未访问元素加入q,q={5,7,8}。
从队列中取出队首5,q={7,8}。然后将和5相连的未访问元素加入q,q={7,8,6}。
从队列中取出队首7,q={8.6}。然后将和7相连的未访问元素加入q,q={8,6,A,9}。
从队列中取出队首8,q={6,A,9}。然后将和8相连的未访问元素加入q,q={6,A,9}。
从队列中取出队首6,q={A,9}。然后将和8相连的未访问元素加入q,q={A,9}。
从队列中取出队首A,q={9}。然后发现找到了目标元素,遂退出。
在这个过程中,有时候还需要记录层数。例如这例中,第一层是1,第二层是2和3,第三层是4、5、7,第四层是8、6、A、9。什么是层数?换言之,你想从1访问到A,A在第四层,也就是说最短步数为4,这个最短路径为1->3->7->A。
(Ⅱ)代码实现
因为这个题我用的是BFS,所以我先写BFS的代码实现。
//BFS搜索
queue q;
bool vis[N] = {false}; //记录点的访问情况。false表示点未被访问,true表示点已经被访问过。
int step[N]; //step表示第N个节点在第几层
//初始化step
memset(step,-1,sizeof(step));
//假设起点为s
q.push(s); //起点入列
vis[s] = true; //将起点设置为被访问过
step[s] = 1; //起点在第一层
while ( q.size() ) { //只要队列内有元素,就一直执行
//从队列中取出队首
int cur = q.top;
q.pop;
//下面是伪代码
for (所有和队首相连的边) {
int v = 边相连的点;
if ( !vis[v] )
{ //如果这个点没被访问过
//那么就把这个点加入队列
q.push(v);
//并且把这个点设置为被访问过
vis[v] = true;
//v的层数是cur的层数+1
step[v] = step[cur] + 1;
}
}
} 代码应该是初学者可以看得懂的,没有涉及到什么复杂的知识。
7、一些补充
以上是我的个人笔记,我承认难度不够深,可能一些描述也不够标准。但是对入门来说应该很合适,提前适应一些基本的代码就够了。
三、思路分析
首先很容易想到,对于每一个“成语”,我们只需要它的首尾,中间两位其实不重要。
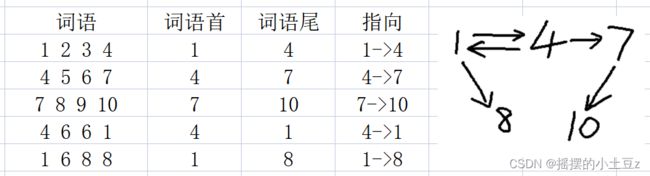
这就会想到有向图,一个词语中每个字的顺序是固定的,可以看成词首指向词尾。词语1 2 3 4,可以看成是1指向了4,于是,对于用例1的五个成语可以绘制成下面的图:
需要统计这个过程中经过的边数。
四、代码实现
如何建图?考虑map中每一个结点对应的是一个数组,数组中储存的是与之相连的结点。
queue q;
map< int,vector > g;
//建图
int m;
scanf("%d",&m);
int t1,t2;
for (int i=0;i 之后按照上面的伪代码,基本不差。
输出最终词语词尾的step(层数)即可。
再说一次,这篇文章相当于是对学长已发帖子的一篇小翻译,还是向学长表示我的谢意呜呜呜,感谢学长!