【2022年省赛Java A组真题】-蓝桥杯【拿了国一】
2022年省赛Java A组真题-蓝桥杯
2023年6月22日更新
国赛成绩出了,拿了国一(Java研究生组),兄弟们加油!!
✨✨备战2023年蓝桥杯,一起冲鸭!!
这些题目跟力扣好不一样啊。力扣上的部分简单题有固定的套路,很容易想出来。而蓝桥杯脑筋急转弯、数学、推公式题目占大多数,且每题数据范围都很大,想AC必须想出来最佳解。
最短路、欧拉筛&线性筛、平方和公式等,后边还得复习复习。
A、裁纸刀
题目
小蓝有一个裁纸刀,每次可以将一张纸沿一条直线裁成两半。
小蓝用一张纸打印出两行三列共 6 个二维码,至少使用九次裁出来,下图给出了一种裁法。
在上面的例子中,小蓝的打印机没办法打印到边缘,所以边缘至少要裁 4 次。另外,小蓝每次只能裁一张纸,不能重叠或者拼起来裁。
如果小蓝要用一张纸打印出 20 行 22 列共 440 个二维码,他至少需要裁多少次?
解题思路
问至少要裁多少次,那么尽量让每一次裁剪覆盖到尽可能多的边,因此每一次裁剪都要头裁剪到尾部,而不会说是裁剪到中间就停止了(能裁就裁)。
- 对于外部的边,需要裁4次,这是固定的
- 而对于内部的边,有两种情况:设行数为
r,列数为c,先裁剪行再裁剪列,需要的裁剪数为(r-1)+(r×(c-1))=rc-1。先裁剪列再裁剪行,需要的裁剪数为(c-1)+(c×(r-1))=rc-1。说明两种方式得到的结果是一样的。将r=20,c=22代入得20×22-1=439。
因最终需要的裁剪次数为4+439=443次
B、寻找整数(后续补充)
问题
有一个不超过 1e17 的正整数n,知道这个数除以 2 至 49 后的余数如下表所示,求这个正整数最小是多少。
解题思路
C、求和
问题
给定n个整数a1,a2,…,an,求它们两两相乘再相加的和,即:
S=a1×a2+a1×a3+…+a1×an+a2×a3+…+an-2×an-1
输入格式
输入的第一行包含一个整数 n。
第二行包含 n 个整数a1,a2,…,an
输出格式
输出一个整数 S,表示所求的和。请使用合适的数据类型进行运算。
解题思路:乘法分配律+后缀和
这道题数据范围为2e5,如果两层循环肯定是过不了的。对于S,可以使用乘法分配律,将a1提取出来得到a1×(a2+a3…+an),提取a2得到a2×(a3+a4…+an),这样的话也就是求ai×(ai+1…+an)的和,其中i∈[1,n]。因此我们需要预处理一个后缀和数组,然后从头到尾遍历,求和得到最终的结果,主要要用long类型。
import java.util.Scanner;
public class C {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 乘法分配律+后缀和
int n=scan.nextInt();
int[] nums=new int[n];
for(int i=0;i<n;i++) {
nums[i]=scan.nextInt();
}
// 预处理后缀和
int[] suffixSum=new int[n+1];
for(int i=1;i<=n;i++) {
suffixSum[i]=suffixSum[i-1]+nums[i-1];
}
// 1e6 2e5 2e5
long ans=0L;
for(int i=1;i<=n;i++) {
ans+=(long)nums[i-1]*(suffixSum[n]-suffixSum[i]);
}
System.out.println(ans);
scan.close();
}
}
D、GCD
问题描述
给定两个不同的正整数 a,b, 求一个正整数 k 使得 gcd*(a+k,b+k) 尽可能大, 其中 gcd(a,b) 表示 a* 和 b 的最大公约数, 如果存在多个 k*, 请输出所有满 足条件的 k* 中最小的那个。
输入格式
输入一行包含两个正整数 a*,*b, 用一个空格分隔。
输出格式
输出一行包含一个正整数 k 。
解题思路:更相减损术的性质
利用根据更相减损术的性质:gcd(a,b)=gcd(a,a-b)=gcd(b,a-b)
证明:a-b=c,设gcd(a,b)=k,则a=k×p,b=k×q,其中p与q互质(若不互质,则a与b的最大公因数就不是k了,与假设不符)。a-b=k×(p-q),而(p-q)与p和q都互质(如果被减数与减数互质,则被减数,减数,差都是互质的,证明在后面)。因此gcd(a,a-b)=gcd(b,a-b)=gcd(a,b)。
如果被减数与减数互质,则被减数,减数,差都是互质的:x与y互质,z=x-y,假设z与y有公因数。设z与y的公因数为k,y=p×k,z=q×k -> x=(p+q)×k,这样x与y也有因数了,与假设的x与y互质违背。
好,有了这个公式之后,题目要求gcd(a+k,b+k),则根据这个公式可以得到gcd(a+k,b+k)=gcd(a,a-b)=gcd(b,a-b),而gcd(a,a-b)的最大公因数为a-b,因此gcd(a+k,b+k)的最大公因数就是a-b。因此,我们要求最小的k,使得a+k与b+k是a-b的倍数。
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
long a=scan.nextLong(),b=scan.nextLong();
long c=Math.abs(a-b);
System.out.println(-a%c+c);
scan.close();
}
public static long gcd(long x,long y) {
return x%y==0?y:gcd(y,x%y);
}
}
E、蜂巢
问题描述
蜂巢由大量的六边形拼接而成, 定义蜂巢中的方向为: 0 表示正西方向, 1 表示西偏北 60∘,2 表示东偏北 60∘,3 表示正东, 4 表示东偏南 60∘,5表示西偏南 60∘ 。
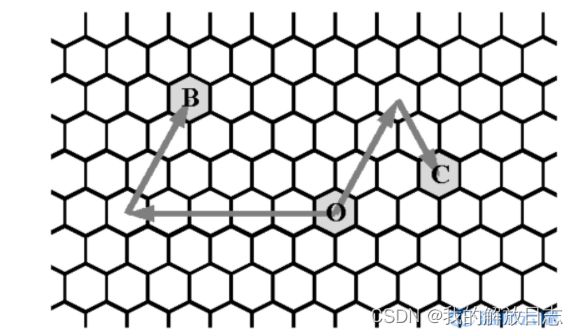
对于给定的一点 O, 我们以 O 为原点定义坐标系, 如果一个点 A 由 O 点 先向 d* 方向走 p 步再向 (d+2) mod 6 方向 ( d 的顺时针 120∘ 方向) 走 q 步到 达, 则这个点的坐标定义为 (d,p,q) 。在蜂窝中, 一个点的坐标可能有多种。
下图给出了点 B*(0,5,3) 和点 C(2,3,2) 的示意。
给定点 (d1,p1,q1) 和点(d2,p2,q2), 请问他们之间最少走多少步可以到达?
输入格式
输入一行包含 6 个整数 d*1,p1,q1,d2,p2,*q2 表示两个点的坐标, 相邻两个整 数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示两点之间最少走多少步可以到达。
解题思路
我是如上图当作x轴和y轴,然后计算出给出的两点以O为原点的坐标。
总共六个方向,往每个方向走对应x,y坐标的变化为{-1,0},{0,1},{1,1},{1,0},{0,-1},{-1,-1},可以看到当x与y同时需要增加时,仅需走1步即可,而不用先走x轴,再走y轴。举个例子:例如我们需要从点(1,1)走到点(2,2),如果先走方向1再走方向3,需要2步。但是往方向2走一步,x,y坐标变化为{1,1},这样1步便可以走到(2,2)。因此,我们总结思路:能同时逼近x和y的话,尽量同时逼近,否则再一步一步走。代码如下。
import java.util.Scanner;
public class E {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int d1=scan.nextInt();
int p1=scan.nextInt();
int q1=scan.nextInt();
int d2=scan.nextInt();
int p2=scan.nextInt();
int q2=scan.nextInt();
int[][] dirs=new int[][] {{-1,0},{0,1},{1,1},{1,0},{0,-1},{-1,-1}}; // 6个方向
// 计算坐标
long x1=(long)p1*dirs[d1][0]+q1*dirs[(d1+2)%6][0];
long y1=(long)p1*dirs[d1][1]+q1*dirs[(d1+2)%6][1];
long x2=(long)p2*dirs[d2][0]+q2*dirs[(d2+2)%6][0];
long y2=(long)p2*dirs[d2][1]+q2*dirs[(d2+2)%6][1];
long ans=0L;
long r_step=Math.abs(x1-x2); // 横向走的步数
long c_step=Math.abs(y1-y2); // 纵向走的步数
// 尽量斜着走
if((x1-x2)*(y1-y2)>0) {
long i_step=Math.min(r_step, c_step); // 斜着走的步数
r_step-=i_step;
c_step-=i_step;
ans=i_step;
}
ans+=r_step+c_step;
System.out.println(ans);
scan.close();
}
}
F、全排列的价值
题目描述
对于一个排列 A = (a1, a2, · · · , an),定义价值 ci 为 a1 至 ai−1 中小于 ai 的数的个数,即 bi = |{aj | j < i, aj < ai}|。定义 A 的价值为![]()
给定 n,求 1 至 n 的全排列中所有排列的价值之和。
输入格式
输入一行包含一个整数 n 。
输出格式
输出一行包含一个整数表示答案,由于所有排列的价值之和可能很大,请输出这个数除以 998244353 的余数。
样例输入
3
样例输出
9
解题思路:
对于任意一个数对(x,y),x 这题有几个样例数据太大了,在编码过程中要注意不能溢出了!! 小青蛙住在一条河边,它想到河对岸的学校去学习。小青蛙打算经过河里的石头跳到对岸。 河里的石头排成了一条直线,小青蛙每次跳跃必须落在一块石头或者岸上。不过,每块石头有一个高度,每次小青蛙从一块石头起跳,这块石头的高度就会下降 1,当石头的高度下降到 0 时小青蛙不能再跳到这块石头上(某次跳跃后使石头高度下降到 0 是允许的)。 小青蛙一共需要去学校上 x 天课,所以它需要往返 2x 次。当小青蛙具有一个跳跃能力 y 时,它能跳不超过 y 的距离。 请问小青蛙的跳跃能力至少是多少才能用这些石头上完 x 次课。 输入的第一行包含两个整数 n, x,分别表示河的宽度和小青蛙需要去学校的天数。请注意 2x 才是实际过河的次数。 第二行包含 n − 1 个非负整数 H1, H2, · · · , Hn-1,其中 Hi > 0 表示在河中与小青蛙的家相距 i 的地方有一块高度为 Hi 的石头,Hi = 0 表示这个位置没有石头。 输出一行,包含一个整数,表示小青蛙需要的最低跳跃能力。 由于只有两块高度为 1 的石头,所以往返只能各用一块。第 1 块石头和对岸的距离为 4,如果小青蛙的跳跃能力为 3 则无法满足要求。所以小青蛙最少需要 4 的跳跃能力。 对于 30% 的评测用例,n ≤ 100; 对于 60% 的评测用例,n ≤ 1000; 对于所有评测用例,1 ≤ n ≤ 105 , 1 ≤ x ≤ 109 , 1 ≤ Hi ≤ 104。 1、 2、小青蛙跳过去与调回来是等价的操作,即如果存在几块石头能使得小青蛙到河对岸去,那么这几块石头必然也可以使小青蛙从对岸跳回来。因此,题目中的往x次,返x次,可以转化为往的 3、小青蛙每一次跳跃 根据以上三点,我们可以写出以下代码(栈版本的): 还可以使用 记 f(x) 为 x 的所有因数的平方的和。例如:f(12) = 12 + 22 + 32 + 42 + 62 + 122。 定义 输入一行包含一个正整数 n。 输出一个整数表示答案 g(n) 除以 109 + 7 的余数。 对于 20% 的评测用例,n ≤ 105。 对于 30% 的评测用例,n ≤ 107。 对于所有评测用例,1 ≤ n ≤ 109。 未完待续…,目前先写到这了import java.util.Scanner;
public class F_2 {
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
long n=scan.nextLong();
// 对于(x,y)在一半的排列中x
G、青蛙过河
题目描述
输入格式
输出格式
样例输入
5 1
1 0 1 0
样例输出
4
提示
解题思路:
求跳跃能力至少是多少这点很容易联想到二分,难就难在check()怎么写2x。尽量往远的跳,也就是说如果cur+y有石头,那么就跳到cur+y,否则检查能否跳到cur+y-1,依次类推,如果cur-cur+y之间都不能跳跃,那么就无路可走了,小青蛙跳不过去了。这个可以用并查集或栈来维护。import java.util.ArrayDeque;
import java.util.Arrays;
import java.util.Deque;
import java.util.Scanner;
/**
*
* @author Sunny
* 使用栈维护当前位置能跳的最远的、高度非0的石头
* 最后三个点超时了
*/
public class G {
public static int load[];
public static int[] stone;
public static int n;
public static int x;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
n=scan.nextInt(); // 河的宽度
x=scan.nextInt(); // 上学天数
load=new int[n+1]; // 每块石头负载了多少次小青蛙的跳跃
stone=new int[n]; // 石头的高度
for(int i=1;i<n;i++) {
stone[i]=scan.nextInt();
}
// 二分
int l=1,r=n;
while(l<r) {
int mid=(r-l)/2+l;
if(!check(mid)) {
l=mid+1;
}else {
r=mid;
}
}
System.out.println(l);
scan.close();
}
// mid是跳跃能力
public static boolean check(int mid) {
Arrays.fill(load,0);
load[0]=2*x; // 这里load[0]代表起始位置,需要负载2*x次跳跃
// 栈
Deque<int[]> stack=new ArrayDeque<>();
for(int i=1;i<mid;i++) {
stack.offerLast(new int[] {i,stone[i]});
}
// 判断 i 处的小青蛙,是否每次都能跳到i的右边
// 当所有小青蛙都能跳到n-mid及后边时 仅需一次跳跃即可到达河岸,因此无需往后遍历了
for(int i=0;i<n-mid;i++) {
// 跳跃范围内新增了一块石头
if(stone[i+mid]!=0) stack.offerLast(new int[] {i+mid,stone[i+mid]});
int temp=load[i];
while(temp>0 && !stack.isEmpty()) {
int[] rightStone=stack.pollLast(); // 能跳到的最靠右的石头
if(rightStone[0]<=i) return false; // 不能跳到i之前
int mi=Math.min(rightStone[1], temp); // 这块石头可能能负载完,也可能负载不完
rightStone[1]-=mi;
temp-=mi;
load[rightStone[0]]+=mi;
if(rightStone[1]!=0) {
// 跳完石头还有剩余,还需要加入栈中
stack.offer(rightStone);
}
}
if(temp>0) return false;
}
return true;
}
}
并查集来维护上一个可用的石头:import java.util.Arrays;
import java.util.Scanner;
// 再写一版并查集
// 原来并查集还能干这事
public class G_2 {
public static int load[];
public static int[] stone;
public static int n;
public static int x;
public static int[] p;
public static int[] s;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
n=scan.nextInt(); // 河的宽度
x=scan.nextInt(); // 上学天数
load=new int[n+1]; // 每块石头的负载
p=new int[n+1]; // 并查集
s=new int[n+1]; // 石头高度的临时变量
stone=new int[n]; //
for(int i=1;i<n;i++) {
stone[i]=scan.nextInt();
}
// 二分
int l=1,r=n;
while(l<r) {
int mid=(r-l)/2+l; // 2 5
if(!check(mid)) {
l=mid+1;
}else {
r=mid;
}
}
System.out.println(l);
scan.close();
}
public static boolean check(int mid) {
// 从0开始跳尽量 0 -> n
Arrays.fill(load,0);
load[0]=2*x;
// 石头高度数组复制一份
s=Arrays.copyOf(stone, n+1);
// 并查集初始化,每个元素指向自己
for(int i=1;i<n;i++) {
p[i]=i;
}
for(int i=0;i<n-mid;i++) {
// 第i个石头比第i-1个石头可以跳的范围远了1,可选择的石头多了一个
int temp=load[i];
while(temp>0) {
// 根据并查集维护的最靠后的 且 高度不为0的石头
int rightStone=find(i+mid);
if(rightStone<=i) return false; // 不能跳到i之前
int mi=Math.min(s[rightStone], temp);
s[rightStone]-=mi;
temp-=mi;
load[rightStone]+=mi;
// 如果该石头耗尽,则并查集指向前面的石头
if(s[rightStone]==0) {
union(rightStone-1,rightStone);
}
}
}
return true;
}
public static int find(int x) {
return p[x] = (p[x]==x?x:find(p[x]));
}
public static void union(int x,int y) {
int px=find(x);
int py=find(y);
// 这里应该是大的指向小的
if(px>py) {
int temp=px;
px=py;
py=temp;
}
p[py]=px;
}
}
H、因数平方和
题目描述
![]()
。给定 n, 求 g(n) 除以 109 + 7 的余数。输入格式
输出格式
样例输入
100000
样例输出
680584257
提示
解题思路: