一起学数据结构（5）——栈和队列
1. 栈的相关定义及特点：
1. 栈的相关定义：
在正式介绍栈的定义之前，首先来回顾一下关于线性表的定义：
线性表是具有相同数据类型的
个数据元素的有限序列，其中为表长。当
时，可以把线性表看作一个空表，一个典型的线性表就是
英文字母组成的序列，即：
在之前介绍线性表的文章中，解释并实现了线性表的某些功能，例如：头插、尾删、任意位置插入结点等。对于线性表而言，其相对于链表的优点有可以随机访问结点。当利用线性表对任意位置插入结点时，其时间复杂度为
，会过于繁琐。
在上面简要给出线性表的相关内容后，下面给出栈的基本定义：
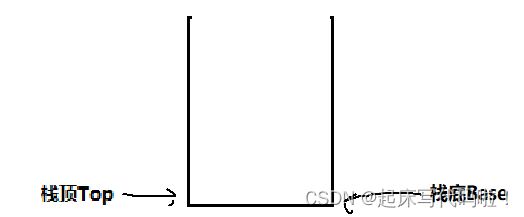
栈(Stack)是一种特殊的线性表，但是与上面所说明的线性表不同的是，栈是一种只能在表尾进行插入、删除操作的线性表。即：
对于上面给出的栈的简要示意图，将表尾（即
)称之为栈顶Top,将表头（即
)称之为栈底Base，因此，上面所提到栈是一种只能在表尾进行插入、删除的数据表这一概念，在这里也可以解释为，栈是一种只能在栈顶Top进行插入、删除操作的线性表。并且，将从栈顶Top插入元素的这一操作命名为进栈，将在栈顶Top进行删除的这一操作命名为出栈。
1.2 栈的特点及相关应用：
对于上面所提到的进栈、出栈这两个操作，可以通过下面的图形进行表示：
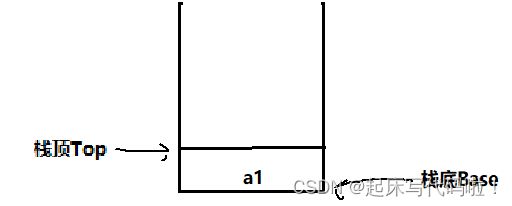
将下面给出的图形定义为空栈
由上面给出的关于栈底、栈顶的相关定义可知，因为此时的栈为空，所以，栈底、栈顶指向同一位置。
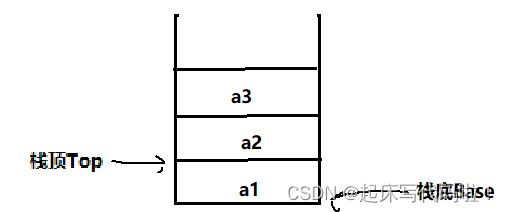
当元素进行入栈操作时，栈、栈底、栈顶的变化可以用下面的图形进行表示：
在元素完成入栈后，栈底Base不变，栈顶Top指向的位置发生变化。一般来说，栈顶Top用来记录栈中完成入栈的元素个数。
如果，再向上面给出的栈中入栈两个元素
。即：
对上面的栈进行出栈操作时，由上面给出的关于出栈的定义可知，出栈的元素顺序为：
所以，栈也可以看作一个具有后进先出特点的线性表。
介于栈后进先出的这一特点，栈可以用于解决许多的实际问题，例如：数制转换、括号匹配检验、表达式求值等。在文章最后会详细解释括号匹配检验问题。
2. 栈的代码实现（顺序栈的实现）：
2.1 栈结构创建：
采用结构体对栈的结构进行创建，其中静态的栈结构如下：
#define N 10;
struct Stack
{
int arr[N];
int top;
};在前面实现顺序表时就提到，在采用静态方式来实现栈或者顺序表等数据结构时，由于内存大小不能进行灵活的调整，很容易就会造成内存浪费或者越界等问题。本文依旧采用动态开辟内存的方式来实现对栈结构的创建。代码如下：
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;其中，
表示栈顶。用于后续的插入删除等操作的实现。
用于表示栈中被使用的空间大小，一旦使用的空间大小达到，就立刻进行扩容。
2.2 栈的初始化：
定义函数
用于初始化上面创建的栈的结构。其中，需要进行的操作为：
1.动态开辟一定大小的空间。或者直接将结构体中创建的指针
初始化为
.后续进行扩容。因为在顺序表中采用了第一种方式。所以，对于栈的初始化，采用第二种
2.初始化时，栈为空栈，所以将和初始化为
代码如下：
//栈的初始化：
void STInit( ST* ps )
{
assert(ps);
ps->a = NULL;
ps->top = ps->capacity = 0;
}2.3 栈的销毁：
对于栈的销毁，同样可以分为下面几步：
1.
指针所指向的动态开辟的空间。
2.将指针中存储的地址改为
3.将
都改为0
代码如下：
//栈的销毁：
void STDestory(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}2.4 通过栈顶向栈中插入元素：
对于通过栈顶向栈中插入元素这一功能，可以分为下面几步进行实现：
1.前面说到，为了演示扩容的第二种方式，所以在通过栈顶向栈中插入元素这一操作时，首先需要检查表示栈中已有元素数量的变量是否与表示栈容量的变量相等。若相等，则表示此时栈空间已满需要啊进行扩容。
2.在扩容完毕之后，需要将表示容量的变量的大小进行更改。并且将用于扩容的指针变量中的值赋值给。
3.此时指针变量中存储了动态开辟的空间的地址，通过![ps->a[ps->top] = x](http://img.e-com-net.com/image/info8/6a0654c97bc0458f8b158042eedf8181.png){kind=small}
来完成插入元素的目的。
4.将
代码如下：
void STPush(ST* ps, STDataType x)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newcapacity = ps->capacity == 0 ? ps->capacity = 4: ps->capacity * 2;
STDataType* newnode = (STDataType*)realloc(ps->a,sizeof(STDataType) * newcapacity);
if (newnode == NULL)
{
perror("realloc");
}
ps->a = newnode;
ps->capacity = newcapacity;
}
ps->a[ps->top] = x;
ps->top++;
}2.5 删除栈中的元素：
在上面通过栈顶向栈中插入元素的操作中，![ps->a[ps->top] = x;](http://img.e-com-net.com/image/info8/e9ac44f28f414024af217febff3b52ce.png){kind=small}
表示，插入元素时,是通过![a[ps->top]](http://img.e-com-net.com/image/info8/3e5c7e8564a6410bb94d28982554b286.png){kind=small}
来访问数组并且进行插入的。所以，对于删除栈中的元素。只需要将
即可。代码如下：
void STPop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}2.6 探空：
用于判断此时的栈是否为空栈，所以，只需要检测
即可，代码如下：
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
2.7 求栈的长度：
对于栈的长度，也就是栈中插入了几个元素。可以通过栈顶进行反应：
int size(ST* ps)
{
assert(ps);
return ps->top;
}2.8 取栈顶元素：
与通过栈顶向栈中插入元素的大致思路相同，通过![ps->a[top-1]](http://img.e-com-net.com/image/info8/fc22787bfb0e4d90ad5dd5dbd095fbfd.png){kind=small}
达到取栈顶元素的目的，代码如下：
STDataType STTop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->a[ps->top-1];
}3. 与栈相关的题目解析——Leetcode.20——有效的括号：
3.1 题目解析：
题目要求在判断有效字符串时，需要满足相同类型的括号闭合，以及正确的闭合顺序。对于正确的闭合顺序这一要求，决定了题目不能使用数组来统计不同类型的括号的数量，判断相同类型阔号的数量是否为偶数来解决问题。
在栈的特点这一部分的内容中提到，栈可以看作有后进先出特点的线性表。介于这个特点可以用栈来解决此题。
具体思路如下：
1. 采用
循环对给定字符串的每个字符遍历，检测被遍历的字符是否为三个括号：‘（‘，’[’，‘{’其中之一，满足条件则将这个字符入栈。
2. 当遇到字符串为‘）’，‘]’，‘}’，时，将栈中已经记录的字符出栈，并且额外创建一个变量记录。进行匹配。如果此时遇到的字符串与出栈的字符串不满足题目中给定的关系，即不满足每个右括号都有一个对应的相同类型的左括号。则返回
。如果满足则让
指向下一个位置。如果整体字符串都满足上述的对应关系。则返回
。
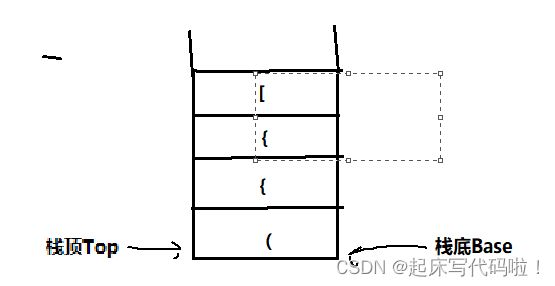
例如，对于字符串"（ { { [ ] } } )"
按照上面所说的步骤，首先将满足‘（’，’[’，‘{’其中之一，满足条件则将这个字符入栈。。此时，栈内的情况可有下面的图进行表示：
这一过程可由下面的代码实现：
while( *s)
{
switch(*s)
{
case '(':
case '[':
case '{':
STPush(&ps,*s);
break;
}
*s++;
}当遍历过程中遇到了右括号，及”] } } )"，开始进行匹配，先创建一个临时变量
用于记录出栈的元素。利用
取出栈顶元素记录在同时，为了下次循环时可以读取到栈后续的内容，需要利用
删除这个元素。
在进行匹配时，只需要考虑匹配不成功的情况。并返回。对于匹配不成功的情况，即左右括号不对称。可以由下面的代码表示：
cur = STTop(&ps);
STPop(&ps);
if( (*s == '}' && cur !='{') || ((*s == ']') && (cur != '[')) || ((*s ==')'))
&& (cur != '('))
{
STDestory(&ps);
return false;
}
break;当字符串中每一个被遍历的字符都匹配成功，说明该字符串是题目要求的有效字符串。不过，再返回之前需要考虑两个特殊情况：
1. 字符串是否只存在左括号，即‘（‘，’[’，‘{’
2. 字符串是否只存在右括号，即‘）’，‘]’，‘}’
3.字符串中左右括号的数量是否相同。
对于情况1，因为不存在右括号，所以在循环的第一部分，即入栈后，就会跳出循环，不参与后续的匹配。所以只需要利用
检测此时的栈是否为空即可。不为空则说明，左右括号数目不相同或者不存在右括号。
对于情况2.因为不存在左括号，所以在循环中经历入栈这个过程时，栈为空。只需要在入栈这个步骤结束后，检测栈是否为空即可。为空则返回即可
对于情况3，在情况一中得到解决。
3.2 代码展示：
（注：79及79行之前的内容为栈的代码实现）
typedef char STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
void STInit( ST* ps )
{
assert(ps);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
//栈的销毁：
void STDestory(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
void STPush(ST* ps, STDataType x)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newcapacity = ps->capacity == 0 ? ps->capacity = 4: ps->capacity * 2;
STDataType* newnode = (STDataType*)realloc(ps->a,sizeof(STDataType) * newcapacity);
if (newnode == NULL)
{
perror("realloc");
}
ps->a = newnode;
ps->capacity = newcapacity;
}
ps->a[ps->top] = x;
ps->top++;
}
void STPop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}
int size(ST* ps)
{
assert(ps);
return ps->top;
}
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
STDataType STTop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->a[ps->top-1];
}
bool isValid(char * s){
ST ps;
STInit( &ps);
char cur;
while( *s)
{
switch(*s)
{
case '(':
case '[':
case '{':
STPush(&ps,*s);
break;
//匹配'{'
case'}':
case']':
case')':
//检测是否存在只有右边有括号的情况
if( STEmpty(&ps))
{
STDestory(&ps);
return false;
}
//取栈顶元素
cur = STTop(&ps);
STPop(&ps);
if( (*s == '}' && cur !='{') || ((*s == ']') && (cur != '[')) || ((*s ==')'))
&& (cur != '('))
{
STDestory(&ps);
return false;
}
break;
}
*s++;
}
//检测是否只有左边有括号的情况，因为在匹配括号时，如果存在右括号
//会使用STTop吸收左括号，所以，如果ret为0，则表示左括号全部吸收完。
bool ret = STEmpty(&ps);
STDestory(&ps);
return ret;
}结果如下：
4. 栈的代码补充：
上面给出的栈并不全面，下面给出头文件
，
#pragma once
#include
#include
#include
#include
//静态栈的创建：
//#define N 10;
//struct Stack
//{
// int arr[N];
// int top;
//};
//栈的动态开辟：
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
//栈的初始化：
void STInit(ST* ps);
//栈的销毁
void STDestory(ST* ps);
//通过栈顶向栈中插入元素
void STPush(ST* ps, STDataType x);
//删除栈中的元素：
void STPop(ST* ps);
//记录size
int size(ST* ps);
//找空
bool STEmpty(ST* ps);
//获取栈顶元素
STDataType STTop(ST* ps);