LeetCode 热题 HOT 100 Java 题解 -- Part 2
练习地址
Part 1 : https://blog.csdn.net/qq_41080854/article/details/128829494
LeetCode 热题 HOT 100 Java 题解 -- Part 2
-
- 37. 二叉树的中序遍历 94
- 38. 不同的二叉搜索树 96
- 39. 验证二叉搜索树 98
- 40. 对称二叉树 101
- 41. 二叉树的层序遍历 102
- 42. 二叉树的最大深度 104
- 43. 从前序与中序遍历序列构造二叉树 105
- 44. 二叉树展开为链表 114
- 45. 买卖股票的最佳时机 121
- 46. 二叉树中的最大路径和 124
- 47. 最长连续序列 128
- 48. 只出现一次的数字 136
- 49. 单词拆分 139
- 50. 环形链表 141
- 51. 环形链表 II 142
- 52. LRU 缓存 146
- 53. 排序链表 148
- 54. 乘积最大子数组 152
- 55. 最小栈 155
- 56. 相交链表 160
- 57. 多数元素 169
- 58. 打家劫舍 198
- 59. 岛屿数量 200
- 60. 反转链表 206
- 61. 课程表 207
- 62. 实现 Trie (前缀树) 208
- 63. 数组中的第K个最大元素 215
- 64. 最大正方形 221
- 65. 翻转二叉树 226
- 66. 回文链表 234
- 67. 二叉树的最近公共祖先 236
- 68. 除自身以外数组的乘积 238
- 69. 滑动窗口最大值 239
- 70. 搜索二维矩阵 II 240
- 72. 完全平方数 279
- 73. 移动零 283
- 74. 寻找重复数 287
- 75. 二叉树的序列化与反序列化 297
- 76. 最长递增子序列 300
- 77. 删除无效的括号 301
37. 二叉树的中序遍历 94
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
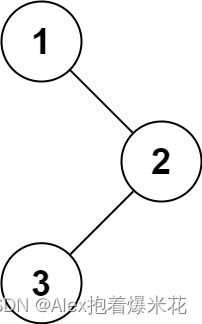
输入:root = [1,null,2,3]
输出:[1,3,2]
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<Integer> res = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
dfs(root);
return res;
}
private void dfs(TreeNode root){
if(root == null) return;
dfs(root.left);
res.add(root.val);
dfs(root.right);
}
}
38. 不同的二叉搜索树 96
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
解析
假设 i 个节点存在二叉排序树的个数是 G (i),令 f(j) 为以 j 为根的二叉搜索树的个数,则
G ( i ) = f ( 1 ) + f ( 2 ) + . . . + f ( j ) G(i) = f(1) + f(2) + ... + f(j) G(i)=f(1)+f(2)+...+f(j)
当 j为根节点时,其左子树节点个数为 j-1 个,右子树节点为 i-j,则
f ( j ) = G ( j − 1 ) ∗ G ( i − j ) f(j) = G(j-1)*G(i - j) f(j)=G(j−1)∗G(i−j)
状态转移方程 G ( n ) = G ( 0 ) ∗ G ( n − 1 ) + G ( 1 ) ∗ ( n − 2 ) + … + G ( n − 1 ) ∗ G ( 0 ) G(n)=G(0) * G(n-1)+G(1) *(n-2)+\ldots+G(n-1) * G(0) G(n)=G(0)∗G(n−1)+G(1)∗(n−2)+…+G(n−1)∗G(0)
代码
class Solution {
public int numTrees(int n) {
int[] dp = new int[n + 1];
dp[0] = 1; //因为要做乘法
for(int i = 1; i < n + 1; i++){ //第几个节点
for(int j = 1; j < i + 1; j++){ //选第几个为根
dp[i] += dp[j -1] * dp[i - j];
}
}
return dp[n];
}
}
39. 验证二叉搜索树 98
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:true
解析
对二叉树进行中序遍历,每遍历到一个节点都和当前已遍历的最后一个节点值比较,只要能满足递增关系就继续遍历,直到遍历所有节点。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
long pre = Long.MIN_VALUE; //前一个的值
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
if(!isValidBST(root.left)) return false;
if(pre >= root.val) return false;
pre = root.val;
return isValidBST(root.right);
}
}
40. 对称二叉树 101
给你一个二叉树的根节点 root , 检查它是否轴对称。
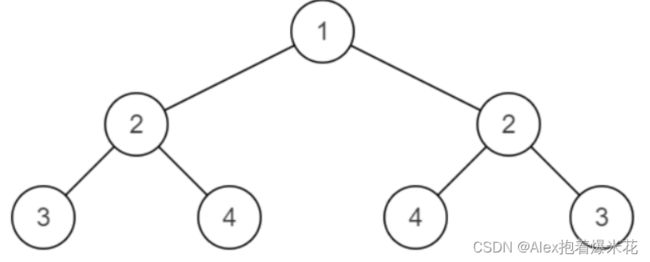
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
解析
判断轴对称,可以看作是判断根节点的左右子树是否镜像,dfs 判断即可。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return dfs(root.left, root.right);
}
private boolean dfs(TreeNode left, TreeNode right){
if(left == null && right == null) return true;
if(left == null || right == null || right.val != left.val) return false;
return dfs(left.left, right.right) && dfs(left.right, right.left);
}
}
41. 二叉树的层序遍历 102
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if(root == null) return new ArrayList<>();
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int n = queue.size();
List<Integer> temp = new ArrayList<>();
while(n-- > 0){
TreeNode node = queue.poll();
temp.add(node.val);
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
}
res.add(new ArrayList(temp));
}
return res;
}
}
42. 二叉树的最大深度 104
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回它的最大深度 3 。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root == null) return 0;
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
}
43. 从前序与中序遍历序列构造二叉树 105
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
解析
二叉树的根节点就是前序序列的第一个节点,这样就可以把中序序列拆分成两部分,根节点前面就是左子树,后面就是右子树,那么就知道了左右子树的节点数量,依此就可以对前序序列也进行拆分,这样左右子树的前序、中序序列都知道了,递归构建左右子树就可以了。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
Map<Integer, Integer> map = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
int n = inorder.length;
for(int i = 0; i < n; i++){
map.put(inorder[i], i); //存放先序
}
return build(preorder, inorder, 0, n - 1, 0, n - 1);
}
private TreeNode build(int[] preorder, int[] inorder, int pl, int pr, int il, int ir){
if(pl > pr || il > ir) return null;
int k = map.get(preorder[pl]) - il;//中序遍历中根节点的位置
TreeNode node = new TreeNode(preorder[pl]);
//左子树
node.left = build(preorder, inorder, pl + 1, pl + k, il, il + k - 1);
//右子树
node.right = build(preorder, inorder, pl + k + 1, pr, il + k + 1, ir);
return node;
}
}
44. 二叉树展开为链表 114
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]。
解析
先序遍历,使用一个pre来记录上一个位置进行修改指向
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
TreeNode pre = null; //上一个位置
public void flatten(TreeNode root) {
if(root == null) return;
//先序遍历
TreeNode l = root.left; //记录下当前节点的左右结点
TreeNode r = root.right;
if(pre == null) pre = root;
else{
pre.right = root; //先序遍历的前一个位置指向当前结点
pre.left = null;
pre = root;// 更新位置
}
flatten(l);
flatten(r);
}
}
45. 买卖股票的最佳时机 121
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
解析
枚举每个位置,在与历史最低价差值最大的价格卖出。贪心算法
代码
class Solution {
public int maxProfit(int[] prices) {
int res = 0, minPrice = prices[0];
for(int i = 1; i < prices.length; i++){
res = Math.max(res, prices[i] - minPrice);
minPrice = Math.min(minPrice, prices[i]);
}
return res;
}
}
46. 二叉树中的最大路径和 124
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
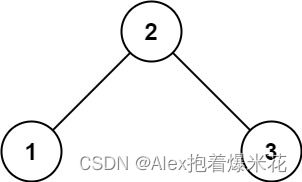
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
解析
通过后序遍历递归得到左右子树的最大路径和,依此来更新结果。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int res = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return res;
}
private int dfs(TreeNode node){
if(node == null) return 0;
//贡献大于0才被选中
int left = Math.max(0, dfs(node.left));
int right = Math.max(0, dfs(node.right));
//计算最大路径和 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
res = Math.max(res, node.val + left + right);
//返回路径的贡献(只能走一条)
return node.val + Math.max(left, right);
}
}
47. 最长连续序列 128
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
解析
使用一个哈希表来记录数组中的数字,然后来遍历哈希表,找到每个连续片段的起点,计算长度即可。
代码
class Solution {
public int longestConsecutive(int[] nums) {
HashSet<Integer> set = new HashSet<>();//连续序列不允许重复
for(int i = 0; i < nums.length; i++){
set.add(nums[i]);
}
int res = 0;
for(int i = 0; i < nums.length; i++){
if(!set.contains(nums[i] - 1)){//找到了起点
int num = nums[i] + 1;
while(set.contains(num)){
num++;
}
res = Math.max(res, num - nums[i]);
}
}
return res;
}
}
48. 只出现一次的数字 136
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1]
输出:1
解析
将数组中所有数字做异或,两两消除,最终剩下的就是只出现一次的元素。
代码
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for(int num : nums){
res ^= num;
}
return res;
}
}
49. 单词拆分 139
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
解析
完全背包,物品之间有序(先背包后物品)
[0, i - 1] 的字符串可被拆分,当且仅当任一子串 [0, j - 1] 及 [j, i - 1] 可被拆分
代码
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
//单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。完全背包问题
//强调物品之间顺序,先背包后物品
int n = s.length();
boolean[] dp = new boolean[n + 1];//定义 f(i) 表示 s 的前 i 个字符能够由字典中单词拼接构成
dp[0] = true;
for(int i = 1; i < n + 1; i++){
for(int j = 0; j < i; j++){
//[0, i - 1] 的字符串可被拆分,当且仅当任一子串 [0, j - 1] 及 [j, i - 1] 可被拆分
if(dp[j] && wordDict.contains(s.substring(j, i))){
dp[i] = true;
break;
}
}
}
return dp[n];
}
}
50. 环形链表 141
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
解析
我们使用两个指针,fast 与 slow。它们起始都位于链表的头部。随后,slow 指针每次向后移动一个位置,而 fast 指针向后移动两个位置。如果链表中存在环,则 fast 指针最终将再次与 slow 指针在环中相遇。
代码
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
if(slow == fast) return true;
}
return false;
}
}
51. 环形链表 II 142
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
解析
我们使用两个指针,fast 与 slow。它们起始都位于链表的头部。随后,slow 指针每次向后移动一个位置,而 fast 指针向后移动两个位置。如果链表中存在环,则 fast 指针重新移动到头部,fast和slow每次往后移动一个位置最终将再次与 slow 指针在环中相遇。
代码
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
if(slow == fast){
fast = head;
while(fast != slow){
fast = fast.next;
slow = slow.next;
}
return fast;
}
}
return null;
}
}
52. LRU 缓存 146
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
解析
哈希表 + 双向链表,哈希表记录 key 和链表节点的映射关系,当需要淘汰时,从链表尾部删除节点;当需要更新时间戳时,通过哈希表获取节点,将其删除并插入到链表头。
代码
//hash表和双向链表
class DNode{ //get
int key;
int value;
DNode pre;
DNode next;
public DNode(){
this.key = 0;
this.value = 0;
this.pre = null;
this.next = null;
}
public DNode(int key, int value){
this.key = key;
this.value = value;
this.pre = null;
this.next = null;
}
}
class LRUCache {
HashMap<Integer, DNode> map; // put
int capacity;
int size;
DNode head;
DNode tail;
public LRUCache(int capacity) {
map = new HashMap<>(capacity);
head = new DNode();
tail = new DNode();
this.capacity = capacity;
this.size = 0;
head.next = tail;
tail.pre = head;
}
public int get(int key) {
if(map.containsKey(key)){
DNode node = map.get(key);
moveToHead(node);
return node.value;
}else{
return -1;
}
}
public void put(int key, int value) {
if(map.containsKey(key)){
DNode node = map.get(key);
moveToHead(node);
node.value = value;
}else{
//判断是否超过容量
DNode node = new DNode(key, value);
map.put(key, node); //map放入对应键
size++;
addToHead(node);//双向链表插入node
//超过容量
if (this.size > this.capacity) {
removeLast();//删除最后一个不用的
size--;
}
}
}
private void moveToHead(DNode node){
//删除结点
node.pre.next = node.next;
node.next.pre = node.pre;
//移动到头部
node.next = head.next;
node.pre = head;
head.next = node;
node.next.pre = node;
}
private void addToHead(DNode node){
node.next = head.next;
node.pre = head;
head.next = node;
node.next.pre = node;
}
private void removeLast(){
DNode node = tail.pre;
map.remove(node.key);
node.pre.next = node.next;
node.next.pre = node.pre;
node.next = null;
node.pre = null;
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/
53. 排序链表 148
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:
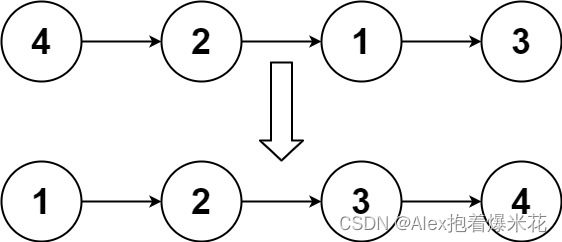
输入:head = [4,2,1,3]
输出:[1,2,3,4]
解析
归并排序
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode sortList(ListNode head) {
if(head == null) return null;
return sort(head);
}
public ListNode sort(ListNode node){
if(node.next == null) return node;//单个结点
ListNode fast = node;
ListNode slow = fast; //中点位置
ListNode pre = null;
//找到中点
while(fast != null && fast.next != null){
pre = slow;
fast = fast.next.next;
slow = slow.next;
}
pre.next = null;
ListNode left = sort(node);
ListNode right = sort(slow);
return merge(left, right);
}
public ListNode merge(ListNode left, ListNode right){
if(left == null) return right;
if(right == null) return left;
ListNode dummy = new ListNode();
ListNode help = dummy;
while(left != null && right != null){
if(left.val > right.val){
help.next = right;
right = right.next;
}else{
help.next = left;
left = left.next;
}
help = help.next;
}
if(left != null) help.next = left;
if(right != null) help.next = right;
return dummy.next;
}
}
54. 乘积最大子数组 152
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
解析
本题与 0053. 最大子序和 的思路相似,但由于是乘法运算,负数相乘可能得到最大值,因此在遍历的同时需要维护最大值和最小值两个变量。
代码
class Solution {
public int maxProduct(int[] nums) {
int res = nums[0];
int f = nums[0];// 最大值
int g = nums[0];// 最小值
for(int i = 1; i < nums.length; i++){
int t = nums[i];
int fa = f * t;
int ga = g * t;
f = Math.max(t, Math.max(fa, ga));
g = Math.min(t, Math.min(fa, ga));
res = Math.max(res, f);
}
return res;
}
}
55. 最小栈 155
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
示例 1:
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
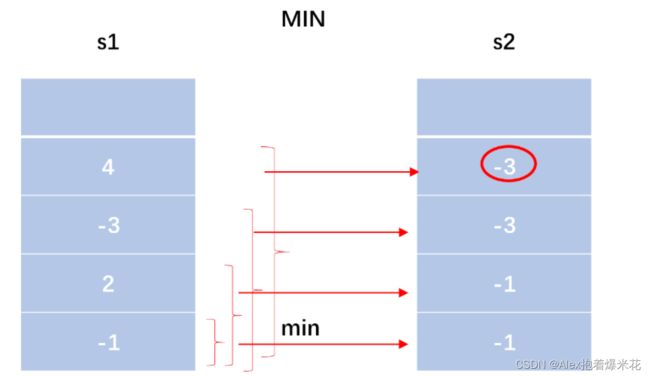
解析
代码
class MinStack {
Deque<Integer> stack;
Deque<Integer> minstack;
public MinStack() {
stack = new ArrayDeque<>();
minstack = new ArrayDeque<>();
}
public void push(int val) {
stack.push(val);
if(minstack.isEmpty() || minstack.peek() > val){
minstack.push(val);
}else{
minstack.push(minstack.peek());
}
}
public void pop() {
stack.pop();
minstack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return minstack.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(val);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.getMin();
*/
56. 相交链表 160
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
解析
统计长度,并且长的先走length,最后一起走就是答案
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int al = 0, bl = 0;
ListNode cur1 = headA;
ListNode cur2 = headB;
while(cur1 != null){
cur1 = cur1.next;
al++;
}
while(cur2 != null){
cur2 = cur2.next;
bl++;
}
if(cur1 != cur2) return null;
cur1 = al - bl < 0 ? headA : headB; // 短的那一节
cur2 = cur1 == headA ? headB : headA;// 长的那一节
// 长的走
for(int i = 0; i < Math.abs(al - bl); i++){
cur2 = cur2.next;
}
// 一起走
while(cur1 != cur2){
cur1 = cur1.next;
cur2 = cur2.next;
}
return cur2;
}
}
57. 多数元素 169
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
解析
Boyer-Moore 投票算法:每次都找出一对不同的元素,从数组中删除,直到数组为空或只有一种元素。
不难证明,如果存在元素 e 出现频率超过半数,那么数组中最后剩下的就只有 e。
代码实现:使用 ans 记录已遍历元素中出现次数最多的元素,count 记录还未被抵消的数量,当遍历结束 ans 即为数组的众数。
代码
class Solution {
public int majorityElement(int[] nums) {
int res = 0, count = 0;
for(int i = 0; i < nums.length; i++){
if(count == 0) res = nums[i];
if(nums[i] != res) count--;
else count++;
}
return res;
}
}
58. 打家劫舍 198
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
解析
动态规划,dp[i] 表示偷第 i 家 获得的最高金额
状态方程 dp[i] = max(dp[i - 1], nums[i -1] + dp[i -2]),不偷这家(累计上次金额)和偷这家(这家金额和累计上上次金额)
代码
class Solution {
public int rob(int[] nums) {
int[] dp = new int[nums.length + 1];
dp[0] = 0; //表示偷第 i 家 获得的最高金额
dp[1] = nums[0];
for(int i = 2; i < nums.length + 1; i++){
dp[i] = Math.max(dp[i - 1], nums[i - 1] + dp[i - 2]);
}
return dp[nums.length];
}
}
59. 岛屿数量 200
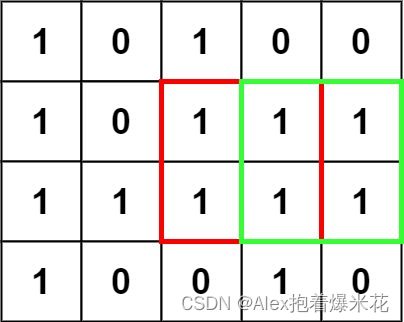
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
解析
- step 1:优先判断空矩阵等情况。
- step 2:从上到下从左到右遍历矩阵每一个位置的元素,如果该元素值为1,统计岛屿数量。
- step 3:接着将该位置的1改为0,然后使用dfs判断四个方向是否为1,分别进入4个分支继续修改。
代码
class Solution {
public int numIslands(char[][] grid) {
int res = 0;
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == '1'){
dfs(grid, i, j);
res++;
}
}
}
return res;
}
private void dfs(char[][] grid, int i, int j){
if(i< 0 || i >= grid.length || j < 0 || j >= grid[0].length //边界条件
|| grid[i][j] == '0') return;
grid[i][j] = '0';
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
}
60. 反转链表 206
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode next = null;
while(head != null){
next = head.next;
head.next = pre;
pre = head;
head = next;
}
return pre;
}
}
61. 课程表 207
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
解析
通过dfs,判断是否有环
代码
class Solution {
List<List<Integer>> graph = new ArrayList<>();
int[] isvisited;
public boolean canFinish(int numCourses, int[][] prerequisites) {
//创建图
for(int i = 0; i < numCourses; i++){
graph.add(new ArrayList<>());
}
isvisited = new int[numCourses];
//添加节点
for(int[] cp : prerequisites){
graph.get(cp[1]).add(cp[0]);
}
//判断每个节点是否有环
for(int i = 0; i < numCourses; i++){
if(hasCircle(prerequisites, i)) return false;
}
return true;
}
private boolean hasCircle(int[][] prerequisites, int index){
if(isvisited[index] == 1) return true;//走到自身,有环
if(isvisited[index] == 2) return false;//走过了,没有环,跳过
isvisited[index] = 1;
for(Integer i : graph.get(index)){ //出度
if(hasCircle(prerequisites, i)) return true;
}
isvisited[index] = 2; //走过无环标记
return false;
}
}
62. 实现 Trie (前缀树) 208
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
Trie 的应用场景,8 个字:一次建树,多次查询。
代码
class Trie {
private TreeNode root;
public Trie() {
root = new TreeNode();
}
public void insert(String word) {
TreeNode node = root;
for(char c : word.toCharArray()){
if(node.next[c - 'a'] == null){
node.next[c - 'a'] = new TreeNode();
}
node = node.next[c - 'a']; //移动下一位
}
node.isEnd = true;
}
public boolean search(String word) {
TreeNode node = root;
for(char c : word.toCharArray()){
node = node.next[c - 'a'];
if(node == null) return false;
}
return node.isEnd;
}
public boolean startsWith(String prefix) {
TreeNode node = root;
for(char c : prefix.toCharArray()){
node = node.next[c - 'a'];
if(node == null) return false;
}
return true;
}
}
class TreeNode{
boolean isEnd;
TreeNode[] next;
public TreeNode(){
isEnd = false; //是否到头
next = new TreeNode[26]; //26个字母,默认为null
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/
63. 数组中的第K个最大元素 215
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
解析
快排,转换为求前N最小
代码
class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSort(nums, 0, nums.length - 1, nums.length - k);
}
public int quickSort(int[] nums, int l, int r, int idx){
if(l == r) return nums[l];
int k = l + (int)(Math.random() * (r - l + 1));
swap(nums, r, k);
int q = partion(nums, l, r);//小于等于区域的右边界
if(q == idx) return nums[q];
else if(q < idx) return quickSort(nums, q + 1, r, idx);
else return quickSort(nums, l, q - 1, idx);
}
private void swap(int[] nums, int a, int b){
int t = nums[a];
nums[a] = nums[b];
nums[b] = t;
}
private int partion(int[] nums, int l, int r){
int cmp = nums[r];
int left = l - 1;
for(int i = l; i < r; i++){
if(nums[i] <= cmp){
swap(nums, i, ++left);
}
}
swap(nums, r, left + 1);
return left + 1;
}
}
64. 最大正方形 221
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
输入:matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出:4
解析
动态规划, d p [ i ] [ j ] dp[i][j] dp[i][j] 表示以 i, j 为右下角的正方形的最大边长
转移方程 d p ( i , j ) = m i n ( d p ( i − 1 , j ) , d p ( i − 1 , j − 1 ) , d p ( i , j − 1 ) ) + 1 dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1 dp(i,j)=min(dp(i−1,j),dp(i−1,j−1),dp(i,j−1))+1
代码
class Solution {
public int maximalSquare(char[][] matrix) {
int r = matrix.length;
int c = matrix[0].length;
int[][] dp = new int[r + 1][c + 1];//dp[i][j] 表示以 i, j 为右下角的正方形的最大边长
int maxSide = 0;
for(int i = 1; i < r + 1; i++){
for(int j = 1; j < c + 1; j++){
if(matrix[i - 1][j - 1] == '1'){
//成为正方形应该是斜上,上 和 左 都 1 , 并且短板效应
dp[i][j] = Math.min(dp[i - 1][j - 1],Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
maxSide = Math.max(maxSide, dp[i][j]);
}
}
}
return maxSide * maxSide;
}
}
65. 翻转二叉树 226
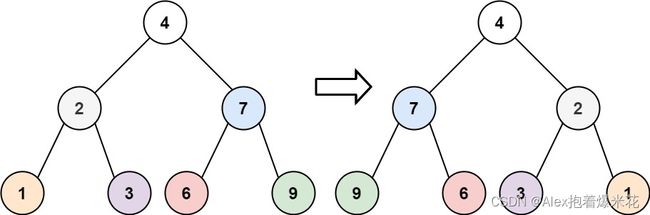
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
解析
先序遍历从顶向下交换即可
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null) return null;
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}
66. 回文链表 234
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
输入:head = [1,2,2,1]
输出:true
示例 2:
输入:head = [1,2]
输出:false
解析
利用快慢指针找到中点,将后半截反序,两个指针从两边遍历到中点,逐个比较
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public boolean isPalindrome(ListNode head) {
ListNode f = head;
ListNode s = head;
while(f != null && f.next != null){
f = f.next.next;
s = s.next;
}
s = reverse(s);
f = head;
while(s != null){
if(s.val != f.val) return false;
s = s.next;
f = f.next;
}
return true;
}
public ListNode reverse(ListNode node){
ListNode pre = null;
ListNode next = null;
while(node != null){
next = node.next;
node.next = pre;
pre = node;
node = next;
}
return pre;
}
}
67. 二叉树的最近公共祖先 236
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
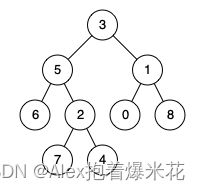
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
if(root.val == p.val || root.val == q.val) return root;//节点为自己的祖先
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left != null && right != null) return root;//从左右子树找到了
return left == null ? right : left;
}
}
68. 除自身以外数组的乘积 238
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
解析
左右累乘,记录每个元素的左右乘积
代码
class Solution {
public int[] productExceptSelf(int[] nums) {
int[] res = new int[nums.length];
int left = 1;
int right = 1;
for(int i = 0; i < nums.length; i++){
res[i] = left;
left *= nums[i];
}
for(int j = nums.length - 1; j >= 0; j--){
res[j] *= right;
right *= nums[j];
}
return res;
}
}
69. 滑动窗口最大值 239
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
解析
单调队列维护窗口的最大值
代码
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
Deque<Integer> deque = new LinkedList<>();
int[] res = new int[nums.length - k + 1];
for(int i = 0; i < nums.length; i++){
while(!deque.isEmpty() && nums[i] > nums[deque.peekLast()]){
deque.pollLast();
}
deque.offerLast(i);
while(!deque.isEmpty() && deque.peekFirst() < (i - k + 1)){
//已经过了窗口
deque.pollFirst();
}
if(i - k + 1 >= 0){
res[i - k + 1] = nums[deque.peekFirst()];
}
}
return res;
}
}
70. 搜索二维矩阵 II 240
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例 1:
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
解析
首先以左下角为起点,若是它小于目标元素,则往右移动去找大的,若是他大于目标元素,则往上移动去找小的。
代码
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int r = matrix.length;
int c = matrix[0].length;
int i = r - 1;
int j = 0;
while(i >= 0 && j < c){
if(matrix[i][j] > target){
i--;
}else if(matrix[i][j] < target){
j++;
}else{
return true;
}
}
return false;
}
}
72. 完全平方数 279
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
解析
完全背包,dp[i] 表示最小需要完全平方数的数量
代码
class Solution {
public int numSquares(int n) {
//完全背包
int[] dp = new int[n + 1]; //dp[i] 表示最小需要完全平方数的数量
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
//物品 和 容量 i * i 价值 为 1
for(int i = 1; i * i < n + 1; i++){ //每一个平方数
int weight = i * i;
for(int j = weight; j < n + 1; j++){ // 整数 n
dp[j] = Math.min(dp[j], dp[j - weight] + 1);
}
}
return dp[n];
}
}
73. 移动零 283
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
使用一个 idx 指针,指向非零元素的最后一个位置,遍历数组,当遇到非零数字时,将其移动到 idx 上,并把 idx 后移。
当遍历结束后,把 idx 后面的位置全部置为 0 即可。
代码
class Solution {
public void moveZeroes(int[] nums) {
int idx = 0;
for(int i = 0; i < nums.length; i++){
if(nums[i] != 0){
nums[idx++] = nums[i];
}
}
while(idx < nums.length) nums[idx++] = 0;
}
}
74. 寻找重复数 287
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
解析
本题可以转换为已知一个有环链表,求出环的入口
代码
class Solution {
public int findDuplicate(int[] nums) {
int s = nums[0], f = nums[nums[0]];// nums[0] 看做是指针,0 也是指针
// 有环链表
while(s != f){
s = nums[s];
f = nums[nums[f]];
}
f = 0;
while(s != f){
s = nums[s];
f = nums[f];
}
return s;
}
}
75. 二叉树的序列化与反序列化 297
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
提示: 输入输出格式与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
解析
先序遍历
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
StringBuilder sb = new StringBuilder();
Queue<String> queue = new LinkedList<>();
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
//先序遍历
serializeHelp(root);
return sb.toString();
}
private void serializeHelp(TreeNode node){
if(node == null){
sb.append("#_");
return;
}
sb.append(node.val);
sb.append("_");
serialize(node.left);
serialize(node.right);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String[] res = data.split("_", -1);
for(String str : res){
queue.offer(str);
}
return deserializeHelp();
}
private TreeNode deserializeHelp(){
//先序遍历
String str = queue.poll();
if(str.equals("#")) return null;
TreeNode node = new TreeNode(Integer.valueOf(str));
node.left = deserializeHelp();
node.right = deserializeHelp();
return node;
}
}
// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));
76. 最长递增子序列 300
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
解析
动态规划, dp[i] 为考虑前 i 个元素,以第 i 个数字结尾的最长上升子序列的长度
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值
每一个i,对应的dp[i](即最长上升子序列)起始大小至少都是是1
代码
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp, 1);
for(int i = 0; i < nums.length; i++){
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int res = 0;
for(int n : dp){
res = Math.max(res, n);
}
return res;
}
}
77. 删除无效的括号 301
给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。
示例 1:
输入:s = “()())()”
输出:[“(())()”,“()()()”]
示例 2:
输入:s = “(a)())()”
输出:[“(a())()”,“(a)()()”]
示例 3:
输入:s = “)(”
输出:[“”]
解析
回溯算法,确定最后的结果长度并决定要不要删除左右括号,边界判断,左括号大于等于右括号
代码
class Solution {
HashSet<String> set = new HashSet<>();
int len = 0;
public List<String> removeInvalidParentheses(String s) {
int lc = 0, rc = 0;//左右括号的数量
for(char c : s.toCharArray()){
if(c == '(') lc++;
else if(c == ')'){
if(lc == 0) rc++;
else lc--;
}
}
//输出字符串的长度
len = s.length() - lc - rc;
dfs(s, 0, 0, 0, "");
return new ArrayList<String>(set);
}
private void dfs(String s, int l, int r, int idx, String p){
if(l < r) return; //右括号 大于 左括号
if(s.length() == idx){
// 结果是否满足长度要求
if(p.length() == len && l == r) set.add(p);
return;
}
char c = s.charAt(idx);
if(c == '('){
dfs(s, l + 1, r, idx + 1, p + c);// 不删
dfs(s, l, r, idx + 1, p);// 删
}else if(c == ')'){
dfs(s, l, r + 1, idx + 1, p + c);
dfs(s, l, r, idx + 1, p);
}else{ // 非括号,不删
dfs(s, l, r, idx + 1, p + c);
}
}
}