代码随想录算法训练营第四十五天|70. 爬楼梯进阶|322. 零钱兑换|279.完全平方数

LeetCode70. 爬楼梯进阶

动态规划五部曲：

        1，确定dp数组以及下标的含义：dp[i]：爬到有i个台阶的楼顶，有dp[i]种方法。

        2，确定递推公式：求装满背包有几种方法，递推公式一般都是dp[i] += dp[i - nums[j]];本题呢，dp[i]有几种来源，dp[i - 1]，dp[i - 2]，dp[i - 3] 等等，即：dp[i - j]。那么递推公式为：dp[i] += dp[i - j]。

        3，dp数组如何初始化：既然递归公式是 dp[i] += dp[i - j]，那么dp[0] 一定为1，dp[0]是递归中一切数值的基础所在，如果dp[0]是0的话，其他数值都是0了。下标非0的dp[i]初始化为0，因为dp[i]是靠dp[i-j]累计上来的，dp[i]本身为0这样才不会影响结果。

        4，确定遍历顺序：这是背包里求排列问题，即：1、2 步 和 2、1 步都是上三个台阶，但是这两种方法不一样！所以需将target放在外循环，将nums放在内循环。每一步可以走多次，这是完全背包，内循环需要从前向后遍历。

        5，举例来推导dp数组

Java代码如下：

    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        int m = 2;
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (i >= j) dp[i] += dp[i - j];
            }
        }
        return dp[n];
    }

LeetCode322. 零钱兑换

动态规划五部曲：

        1，确定dp数组以及下标的含义：dp[j]：凑足总额为j所需钱币的最少个数为dp[j]

        2，确定递推公式：凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]（考虑coins[i]）。所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。递推公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);

        3，dp数组如何初始化：首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;其他下标对应的数值呢？考虑到递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。所以下标非0的元素都是应该是最大值。

        4，确定遍历顺序：本题求钱币最小个数，那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。所以本题并不强调集合是组合还是排列。如果求组合数就是外层for循环遍历物品，内层for遍历背包。如果求排列数就是外层for遍历背包，内层for循环遍历物品。本题的两个for循环的关系是：外层for循环遍历物品，内层for遍历背包或者外层for遍历背包，内层for循环遍历物品都是可以的！那么我采用coins放在外循环，target在内循环的方式。本题钱币数量可以无限使用，那么是完全背包。所以遍历的内循环是正序综上所述，遍历顺序为：coins（物品）放在外循环，target（背包）在内循环。且内循环正序。

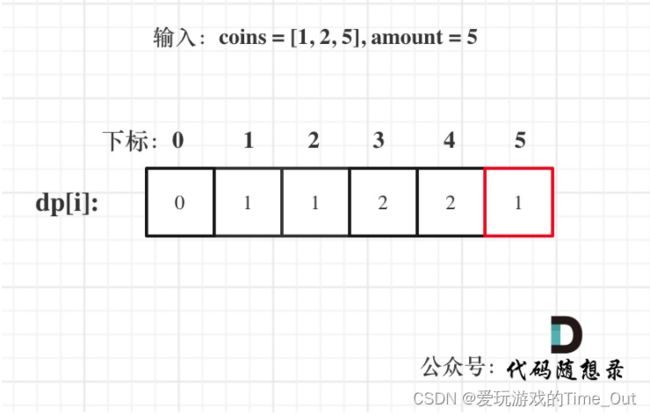
        5，举例推导dp数组：以输入：coins = [1, 2, 5], amount = 5为例：

        dp[amount]为最终结果。

Javad代码如下：

    public int coinChange(int[] coins, int amount) {
        int max = Integer.MAX_VALUE;
        int[] dp = new int[amount + 1];
        for (int j = 0; j < dp.length; j++) {
            dp[j] = max;
        }
        dp[0] = 0;
        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                if (dp[j - coins[i]] != max) {
                    dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
                }
            }
        }
        return dp[amount] == max ? -1 : dp[amount];
    }

LeetCode279.完全平方数

动态规划五部曲：

        1，确定dp数组（dp table）以及下标的含义：dp[j]：和为j的完全平方数的最少数量为dp[j]。

        2，确定递推公式：dp[j] 可以由dp[j - i * i]推出， dp[j - i * i] + 1 便可以凑成dp[j]。此时我们要选择最小的dp[j]，所以递推公式：dp[j] = min(dp[j - i * i] + 1, dp[j]);

        3，dp数组如何初始化：dp[0]表示 和为0的完全平方数的最小数量，那么dp[0]一定是0。有同学问题，那0 * 0 也算是一种啊，为啥dp[0] 就是 0呢？看题目描述，找到若干个完全平方数（比如 1, 4, 9, 16, ...），题目描述中可没说要从0开始，dp[0]=0完全是为了递推公式。非0下标的dp[j]应该是多少呢？从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的，所以非0下标的dp[j]一定要初始为最大值，这样dp[j]在递推的时候才不会被初始值覆盖。

        4，确定遍历顺序：我们知道这是完全背包，如果求组合数就是外层for循环遍历物品，内层for遍历背包。如果求排列数就是外层for遍历背包，内层for循环遍历物品。所以本题外层for遍历背包，内层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的！

        5，举例推导dp数组：已输入n为5例，dp状态图如下：

 

        dp[0] = 0 dp[1] = min(dp[0] + 1) = 1 dp[2] = min(dp[1] + 1) = 2 dp[3] = min(dp[2] + 1) = 3 dp[4] = min(dp[3] + 1, dp[0] + 1) = 1 dp[5] = min(dp[4] + 1, dp[1] + 1) = 2。最后的dp[n]为最终结果。

Java代码如下：

    public int numSquares(int n) {
        int max = Integer.MAX_VALUE;
        int[] dp = new int[n + 1];
        for (int j = 0; j <= n; j++) {
            dp[j] = max;
        }
        dp[0] = 0;
        for (int i = 1; i * i <= n; i++) {
            for (int j = i * i; j <= n; j++) {
                if (dp[j - i * i] != max) {
                    dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
                }
            }
        }
        return dp[n];
    }