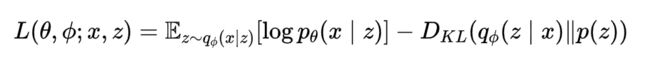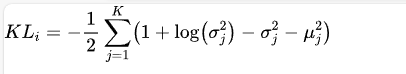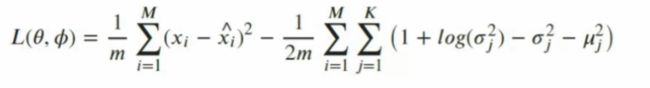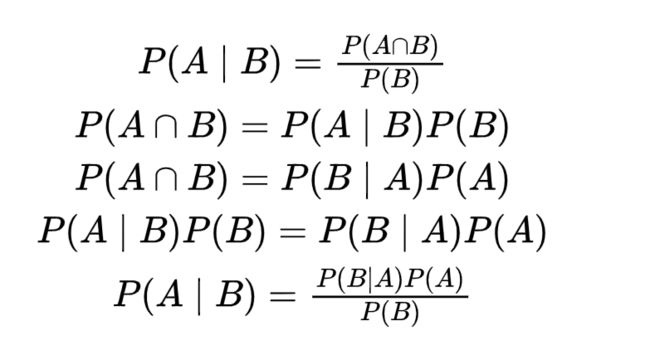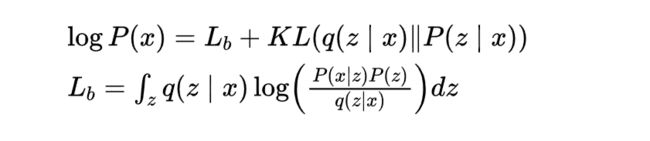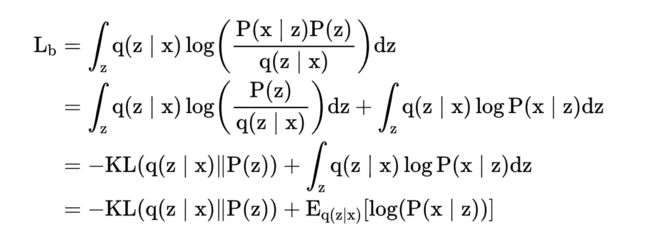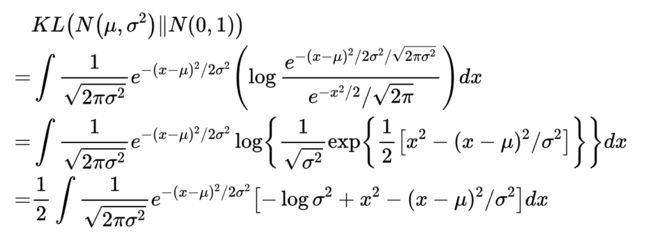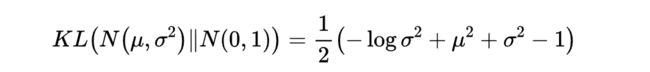【VAE】
个人网站:https://tianfeng.space
一、VAE
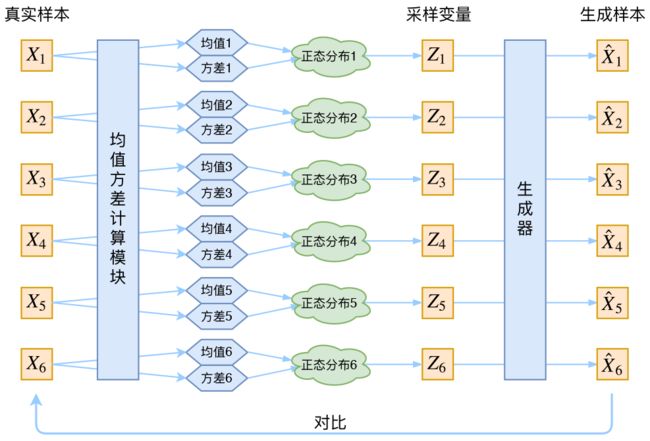
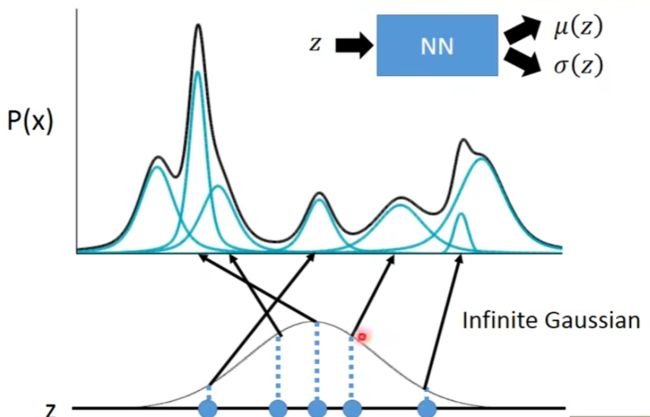
与普通自动编码器一样,变分自动编码器有编码器Encoder与解码器Decoderi两大部分组成,原始图像从编码器输入,经编码器后形成隐式表示(Latent Representation),之后隐式表示被输入到解码器、再复原回原始输入的结构。同时,然而,与普通Autoencoders不同的是,变分自用编码器的Encoder与Decodert在数据流上并不是相连的,我们不会直接将Encoder编码后的结果传递给Decoder,具体流程如下:
1.首先,变分自动编码器中的编码器会尽量将样本所携带的所有特征信息X的分布转码成类高斯分布;,该类高斯分布虽然是以高斯分布为目标来编码的,但它一般无法被编码成完美的高斯分布,这一分布被称之为实际分布Actual Distribution或隐式分布Latent Distribution。
2.编码器需要输出该类高斯分布的均值µ与标准差σ作为编码结果Code
3.以均值µ与标准差σ为基础构建完美的高斯分布Di,这一分布被称之为目标分布Target
Distribution
4.从完美的高斯分布Di中随机抽取出一个数值Zi,将该数值输入解码器
5.解码器基于Zi进行解码,并最终输出与样本的原始特征结构一致的数据,作为变分自动编码器的输出
根据以上流程,变分自动编码器的Encode在输出时,并不会直接输出原始数据的隐式表示,而是会输出从原始数据提炼出的均值和标准差。之后,我们需要建立均值为µ以标准差为σ的正态分布,并从该正态分布中抽样出隐式表示z,再将隐式表示z输入到Decoderr中进行解码。对隐式表示z而言,它传递Decoder的就不是原始数据的信息,而只是与原始数据同均值、同标准差的分布中的信息了。这个流程描述起来似乎并不复杂,但实际的数据流却没有这么简单。在这里,我为大家梳理了三个需要梳理的重点细节:
- 在实际运算当中,Encoder不会先输出di、再根据di计算出μi和σi,而是直接输出满足类正态分布要求的μi和σi,即编码过程中产生的均值与标准差并不是通过均值或标准差的定义计算出来的,而是直接从Encoder网络中输出的值。
- **为了保证Encoder输出的均值和标准差满足类正态分布,变分自动编码器在损失函数中设置了惩罚项,一旦均值和标准差所反馈的分布Actual Distribution与完美的正态分布Target Distribution有差异,变分自动编码器就会受到惩罚。**故而在实际的算法运行流程中,Encoder负责输出均值和标准差,损失函数保证均值和标准差是符合某种类正态分布的,这就等价于Encoder将原始数据向类正态分布的方向编码、再输出该类正态分布的均值与标准差。
- 由于存在随机抽样过程,架构中的数据流是断裂的,因此反向传播无法进行,因此我们需要独特的重参数技巧来完成变分自动编码器的反向传播。这三个细节让整个数据过程变得有些复杂,接下来我们来抽丝剥茧地讲解整个数据过程:
变分自动编码器的数据流
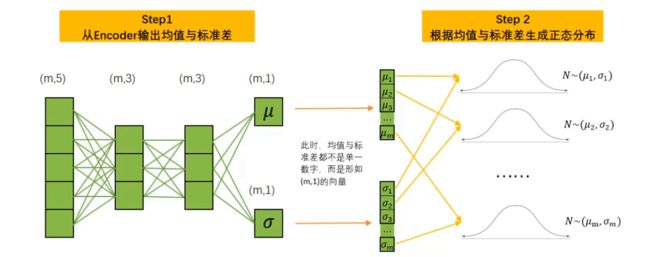
让我们以单一样本和最简单的情况为例,详细讲述一下该过程中的各个细节。首先,假设存在m个样本,5个特征,数据结构为(m,5)。同时,假设Encoder与Decoder中都只有2层带3个神经元的线性层,且每个样本只生成一个均值与一个方差,则转化流程如下所示:
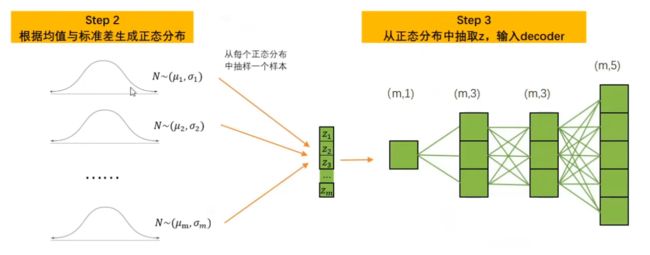
此时,任意样本经过Encoder)后会输出一个均值μi和一个标准差σi,可以认为样本i上所有的特征信息都被认为属于分布N~(μi,σi),故而此时μi,σi已经携带了样本i上尽量多的信息。此时,整个Encoder的输出是形如(m,1)的均值向量μ和标准差向量σ。针对这两个向量中的每一组(μ**,σ),我们都可以生成相应的完美正态分布。有了完美正态分布之后,我们可以从每个正态分布中随机抽选一个数字,并按样本排列顺序拼凑在一起,构成形如(m,1)的z向量。此时,z向量再输入Decoder,Decoder的输入层就只能有1个神经元,因
为z**只有一列。
注意,一组均值和标准差只能生成一个正态分布,而一个正态分布中只能抽选一个数字,这是变分自编码器抽样的基本规则。因此,如果每个样本经过Encoder后只输出了一组均值和标准差,那z自然只能有一列,隐式空间的结构只能为(m,1)。此时,z就是我们抽出的隐式表示,所以Decoder解码的信息都来源于抽样出的样本向量z。大家或许会感觉到奇怪一难道一个样本还可以有多组均值和标准差吗?当然可以。之前我们强调过,在变分自动编码器的流程当中,均值和标准差都不是通过他们的数学定义计算出来的,而是通过Encoder提炼出来的。这就是说当前的均值和标准差不是真实数据的统计量,而是通过Encoder推断出的、当前样本数据可能服从的任意分布中的属性。我们不可能知道当前样本服从的真实分布的状态,因此这一推断过程自然可以根据不同的规则(Encoder中不同的权重)得出不同的结果。
例如,我们可以令Encoder的输出层存在3个神经元,这样Encoder就会对每一个样本推断出三对不同的均值和标准差。这个行为相当于对样本数据所属的原始分布进行估计,但给出了三个可能的答案。因此现在,在每个样本下,我们就可以基于三个均值和标准差的组合生成三个不同的正态分布了。
每个样本对应了3个正态分布,而3个正态分布中可以分别抽取出三个数字z,此时每个隐式表示z就是一个形如(m,3)的矩阵。将这一矩阵放入Decoder,,则Decoder的输入层也需要有三个神经元。此时,我们的隐式空间就是(m3)。
损失函数
公式中的P与q都是分布,一组数据的分布可以由数据本身来表示,也可以由当前数据的均值和标准差来表示。在当前公式当中,两种表示方法我们都有用到。
θ和∅是自动编码器要求解的参数,其中∅是解码器Decoder上各个线性层/卷积层/其它层的参
数,θ是编码器Encoder上各个线性层/卷积层/其它层的参数。
x,z是输入架构的数据,x是输入编码器Encoder的原始数据,z是输入解码器Decoder的原始
数据。
了解这些基本信息后,再来看损失函数公式中被重点突出的部分:
- p(z):z的分布。在整个变分自动编码器中,所有的z都是从正态分布中抽样出来的,因此z的分布就是完美正态分布,也就是之前我们提到的Target Distribution目标分布。
- q∅(z|x):在知晓x的条件下,以∅为参数推断出的z的分布,即以x为输入,以∅为参数推断出的z的具体数据。不难发现,这一过程就是Encoder的过程:因此q∅(z|x)的本质就是Encoder输出层输出的那些均值和标准差,他们代表了我们之前提到的Actual Distribution。
- pθ(x|z):在知晓z的条件下,以θ为参数推断出的x的分布,即以z作为输入,以θ作为参数而推断出的x的具体数据。不难发现,这一过程就是Decoder的过程,所以pθ(x|z)实际上是直接指Decoder的输出。而在公式前的脚标中,特地标注了数据z的来源,不难发现,z~q∅(x|z)说明z是Encoder部分输出的结果,更加佐证了pθ(x|z)是decoder过程的结果。
在这样的状态下,再来解读这一损失函数就容易多了。
损失函数的后半部分
先来看后半部分,这是一个KL散度的计算公式,在原始论文当中被称之为“隐式损失"(Latent Loss)。KL散度是衡量两组数据分布差异的衡量指标,也是衡量分布A在变化成分布B过程中损失的信息量的指标,因此当两组数据的分布越接近时,KL散度就会越小,反之KL散度会越大。
在我们的损失函数当中,很明显KL散度衡量的是Encoder的输出与预设的正态分布之间的差异,这说明损失函数希望Encoder输出的结果越接近正态分布越好,因此在最初介绍自动变分编码器流程时,我们才会认为“变分自动编码器中的编码器会尽量将样本i所携带的所有特征信息Xi的分布转码成类高斯分布Di。这一过程其实并不难理解:在变分自动编码器的Encoder中,我们从原始数据上推断出均值与标准差,并且用这些均值和标准差构筑正态分布,再从正态分布中抽取样本输入Decoder。毫无疑问的,当Encoder输出的数据分布越接近正态分布时,我们所构筑的正态分布才会越靠近原始数据中的信息,从这样的正态分布中抽取的样本才会更接近真实的数据样本。因此KL散度是为了逼迫Encoderl向着正态分布方向解码原始数据而存在的,损失函数中的惩罚项。
一般来说,当我们将从样本生成的均值与标准差带入后,KL散度可以写作:
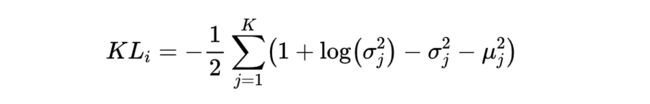
这就是我们在实际执行代码时所写的公式。其中K指的是对一个样本生成了K组均值和标准差,指的是当前
均值和标准差的具体组数,对任意样本,我们需要将全部的K组均值和标准差进行加和后计算。
损失函数的前半部分
现在我们已经了解了损失函数的后半部分了,那它的前半部分是什么呢?虽然无法从肉眼上明显地看出来对Decoder的输出分布求对数是怎样的含义,但变分自动编码器的终极目标依然是输出与原始数据高度相似的数据,因此变分自动编码器的损失函数中必然包含重构损失Reconstruction Lossi这一衡量输入与输出差异的部分。因此很明显,Iog(Decoder输出的分布)就是重构损失。这一形式有些类似于二分类交叉熵中所表示的ylog p(x),只不过我们现在是无监督算法,并无真实标签罢了。在实际的代码执行过程中,我们一般使用MSE或者二分类交叉熵损失的均值来替代上述公式。
重参数化技I巧(reparameterization trick)
现在就是我们要从p(Z|Xk)中采样一个Zk出来,尽管我们知道了p(Z|Xk)是正态分布,但是均值方差都是靠模型算出来的,我们要靠这个过程反过来优化均值方差的模型,但是“采样”这个操作是不可导的,而采样的结果是可导的。我们利用从N(μ,σ2)中采样一个Z,相当于从N(0,I)中采样一个ε,然后让Z=μ+ε×σ
于是,我们将从N(μ,σ2)采样变成了从N(0,I)中采样,然后通过参数变换得到从N(μ,σ2)中采样的结果。这样一来,“采样”这个操作就不用参与梯度下降了,改为采样的结果参与,使得整个模型可训练了。
公式推导
VAE构建两个神经网络来进行拟合均值与方差。左边是q(z|x),右边是p(x|z)
首先P(x) 就是在积分域上所有高斯分布的累加。
- 第一行,左边是Encoder经过x得到的在,对z积分还是1不变,
- 第二行, P(A,B) = P(A|B)*P(B) = P(B|A)*P(A),条件概率和联合概率关系,
- 第五行一样,贝叶斯公式
- 结果第二项就是Kl散度
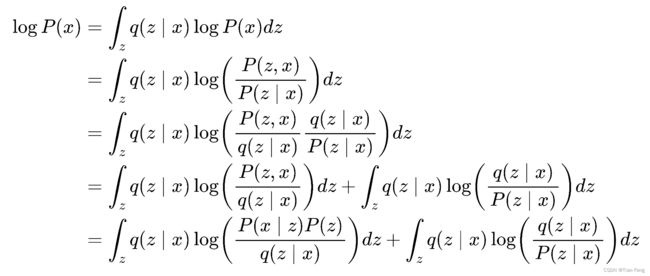
里面包含了朴素贝叶斯公式
紧接着如下
最大化Lb就是最小化KL
整个结果分为三项积分,第一项实际上就是−logσ2乘以概率密度的积分(也就是1),所以结果是−logσ2;第二项实际是正态分布的二阶矩,熟悉正态分布的朋友应该都清楚正态分布的二阶矩为μ2+σ2;而根据定义,第三项实际上就是“-方差除以方差=-1”。所以总结果就是