leetcode第311场周赛题解

最小偶倍数

最小偶倍数
给你一个正整数 n ，返回 2 和 n 的最小公倍数（正整数）。

思路：当n是奇数的时候最小公倍数等于2 * n，否则为n。

也可以用lcm模板来写，代码如下:

int gcd(int a, int b)
{
    if(!b) return a;
    return gcd(b, a % b);
}

class Solution {
public:
    int smallestEvenMultiple(int n) {
        return 2 * n / gcd(2, n);
    }
};

最长的字母序连续子字符串

最长的字母序连续子字符串

考点：遍历。注意：这不是双指针算法，双指针一般指维护一段滑动窗口的算法。

思路：不断枚举起点，然后统计这个起点的最长属性。统计完后跳过这段区间。

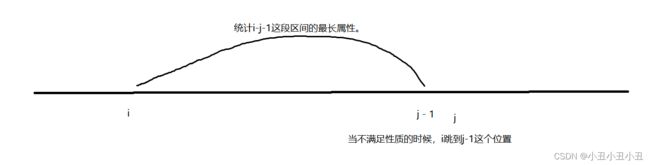
ac代码:

class Solution {
public:
    int longestContinuousSubstring(string s) {
        int res = 0;
        for(int i = 0; i < s.size(); i++)
        {
            int j = i + 1;//终点
            while(j < s.size() && s[j - 1] + 1 == s[j]) j++;//满足性质，j终点往后移动
            res = max(res, j - i);//i - j - 1的长度，实际上就是j - 1 - i + 1
            i = j - 1;//起点跳到终点
        }
        return res;
    }
};

翻转奇数层二叉树

翻转奇数层二叉树

考点：dfs搜索/bfs搜索。注意：这里的翻转指的是镜像翻转，也就是reverse。
比如123456变成654321,而不是214354

bfs方法：可以用层序遍历的方法，当遍历到奇数层，那么就进行reverse操作。如果是偶数层就不管。

bfs的ac代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void bfs(TreeNode* a)
    {
        int levels = 0;
        queue<TreeNode*> q;
        q.push(a);
        while(!q.empty())
        {
        	由于这里要知道是否到达下一层，因此要记录一下一层的大小
            int sz = q.size();
            vector<TreeNode*> v;用来存这一层的所有结点
            for(int i = 0; i < sz; i++)
            {
                TreeNode* t = q.front();
                q.pop();
                if(t->left) q.push(t->left), v.push_back(t->left);
                if(t->right) q.push(t->right), v.push_back(t->right);
            }
            levels++;
            if(levels % 2)
            {
                int l = 0, r = v.size() - 1;
                while(l < r)
                {
                    swap(v[l]->val, v[r]->val);
                    l++, r--;
                }
            }
        }
    }
    TreeNode* reverseOddLevels(TreeNode* root) {
        bfs(root);
        return root;
    }
};

dfs思路：和翻转二叉树思路一样，在这基础上加上是奇数层才翻转这个条件。

注意：翻转的时候由于要达到reverse的效果，因此应该是a的左子树和b的右子树交换，a的右子树和b的左子树交换。

ac代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void dfs(TreeNode* a, TreeNode* b, int level)
    {
        if(!a) return;

        if(level % 2) swap(a->val, b->val);

        dfs(a->left, b->right, level + 1);
        dfs(a->right, b->left, level + 1);
    }
    TreeNode* reverseOddLevels(TreeNode* root) {
        dfs(root->left, root->right, 1);
        return root;
    }
};

两种方法效率差不多。

字符串的前缀分数和

字符串的前缀分数和述

考点：trie树。trie树是以字符串前缀来储存大量字符串的。是一种能够高效存储和查找字符串集合的数据结构。

看到字符串前缀可以考虑使用trie。

案例演示：

若以每一个字符当成结束标志，用trie分析：数字代表以当前字母结尾的字符串有多少个。 比如ab=2代表以ab为前缀的字符串有两个。分别是ab和abc。又比如a=2代表以a为前缀的字符串有两个，分别是ab和abc。

如果用trie本身的结束标志来解释的话，就是当前以该字母的字符串出现了多少次。而出现了一次就代表它肯定是作为了某一个字符串的前缀出现了，因此以它为前缀的次数可以加1

ac代码:

const int N = 1000010;

struct Node
{
    Node* ne[26];
    int cnt;

    Node()
    {
        memset(ne, 0, sizeof ne);
        cnt = 0;
    }
};

class Solution {
public:
    vector<int> sumPrefixScores(vector<string>& words) {
        Node *root = new Node;

        for(auto word : words)
        {
            Node* p = root;
            for(auto ch : word)
            {
                if(!p->ne[ch - 'a']) p->ne[ch - 'a'] = new Node;
                p = p->ne[ch - 'a'];
                每个字符都要cnt++
                p->cnt++;
            }
        }

        vector<int> v;
        for(auto word : words)
        {
            Node* p = root;
            int res = 0;
            for(auto ch : word)
            {
                p = p->ne[ch - 'a'];
                res += p->cnt;
            }
            v.push_back(res);
        }
        return v;
    }
};