LeetCode 第 324场周赛题解
第一题
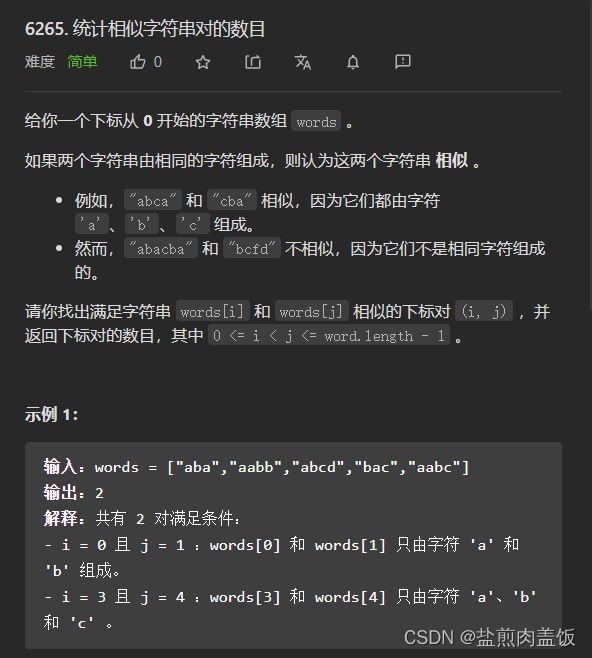
6265. 统计相似字符串对的数目
思路:一道很常规的 比较问题 就是 两两比较就好了
代码:
class Solution {
int res=0;
bool f(string& s1, string& s2)
{
int hash[26];
memset(hash,0,sizeof(hash));
for(int i=0;i& words) {
int n=words.size();
for(int i=0;i 第二题
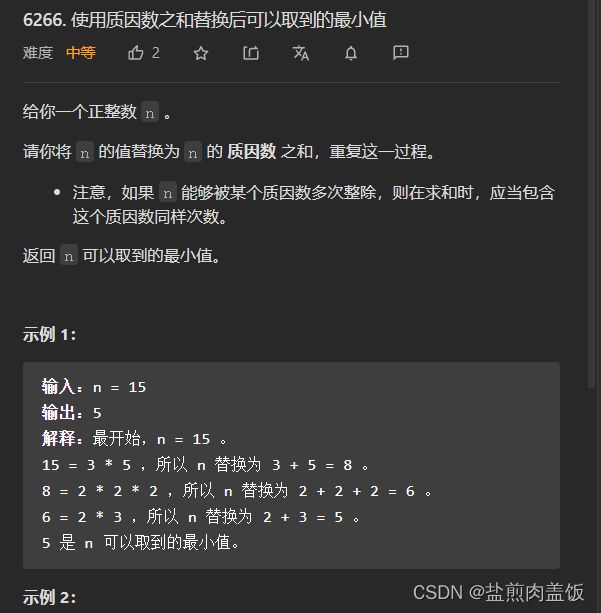
6266. 使用质因数之和替换后可以取到的最小值
思路:先去判断 n是不是 质数 如果是 他就没有质因数 就直接返回n 如果不是的话 就开始循环体 直到 n 变成素数 为止才停下来 用sum变量来接着 n的质因数的和 最后再让n=sum
代码:
class Solution {
bool isprime (int n)
{
for(int i=2;i<=sqrt(n);++i)
{
if(n%i==0) return false;
}
return true;
}
public:
int smallestValue(int n) {
if(n==4) return 4;
while(!isprime(n))
{
int sum=0,i=2;
while(n>1) {
if(n%i==0)
{
sum+=i;
n/=i;
}
else i++;
}
n=sum;
}
return n;
}
};思路: 把度数为奇数的节点记到 \textit{odd}odd 中,记 mm 为 \textit{odd}odd 的长度,分类讨论:如果 m=0m=0,那么已经符合要求。
如果 m=2m=2,记 x=\textit{odd}[0],y=\textit{odd}[1]x=odd[0],y=odd[1]:
如果 xx 和 yy 之间没有边,那么连边之后就符合要求了。
如果 xx 和 yy 之间有边,那么枚举 [1,n][1,n] 的所有不为 xx 和 yy 的点 ii,由于 ii 的度数一定是偶数,如果 ii 和 xx 以及 ii 和 yy 之间没有边,那么连边之后就符合要求了。
如果 m=4m=4,记 a=\textit{odd}[0],b=\textit{odd}[1],c=\textit{odd}[2],d=\textit{odd}[3]a=odd[0],b=odd[1],c=odd[2],d=odd[3]:
如果 aa 和 bb 以及 cc 和 dd 之间没有边,那么连边之后就符合要求了。
如果 aa 和 cc 以及 bb 和 dd 之间没有边,那么连边之后就符合要求了。
如果 aa 和 dd 以及 bb 和 cc 之间没有边,那么连边之后就符合要求了。
其余情况无法满足要求。
代码:
class Solution {
public:
bool isPossible(int n, vector> &edges) {
vector degree(n + 1, 0);
vector g[n + 1];
for (auto it: edges) {
int x = it[0], y = it[1];
degree[x]++;
degree[y]++;
g[x].emplace_back(y);
g[y].emplace_back(x);
}
vector v;
for (int i = 1; i <= n; i++) {
if (degree[i] % 2 == 1) {
v.push_back(i);
}
}
if (v.size() % 2 == 1 || v.size() > 4) return false;
if (v.size() == 0) return true;
if (v.size() == 2) {
if (find(g[v[0]].begin(), g[v[0]].end(), v[1]) == g[v[0]].end())
return true;
else {
for (int i = 1; i <= n; i++) {
if (i != v[0] && i != v[1] && find(g[i].begin(), g[i].end(), v[0]) == g[i].end() &&
find(g[i].begin(), g[i].end(), v[1]) == g[i].end())
return true;
}
}
return false;
}
if (v.size() == 4) {
if (find(g[v[0]].begin(), g[v[0]].end(), v[1]) == g[v[0]].end() &&
find(g[v[2]].begin(), g[v[2]].end(), v[3]) == g[v[2]].end())
return true;
else if (find(g[v[0]].begin(), g[v[0]].end(), v[2]) == g[v[0]].end() &&
find(g[v[3]].begin(), g[v[3]].end(), v[1]) == g[v[3]].end())
return true;
else if (find(g[v[0]].begin(), g[v[0]].end(), v[3]) == g[v[0]].end() &&
find(g[v[2]].begin(), g[v[2]].end(), v[1]) == g[v[2]].end())
return true;
}
return false;
}
}; 第4题
6268. 查询树中环的长度
思路:这道题 可以拆分成求最近公共祖先 和 一个节点的高度 两个问题
代码:
class Solution {
public:
vector cycleLengthQueries(int n, vector>& queries) {
vector ans;
for(auto&query: queries) {
int node1= query[0], node2= query[1];
if((node1 >> 1) == node2 || (node2 >> 1) == node1) ans.push_back(2);
else ans.push_back(LCA(node1, node2));
}
return ans;
}
int LCA(int node1, int node2) {
int n1=node1,n2=node2;
while(node1 != node2) {
if(node1 > node2) node1 >>= 1;
else node2 >>= 1;
}
int h1=get_height(n1), h2=get_height(n2), h=get_height(node1);
return 1+(h1-h)+(h2-h);
}
int get_height(int node) {
int left = 0, right = 29;
while(left < right) {
int mid = right - ((right - left) >> 1);
if(1<