数据结构-堆的实现及应用(堆排序和TOP-K问题)
数据结构-堆的实现及应用[堆排序和TOP-K问题]
- 一.堆的基本知识点
-
- 1.知识点
- 二.堆的实现
-
- 1.堆的结构
- 2.向上调整算法与堆的插入
- 2.向下调整算法与堆的删除
- 三.整体代码
- 四.利用回调函数避免对向上和向下调整算法的修改
-
- 1.向上调整算法的修改
- 2.向下调整算法的修改
- 3.插入元素和删除元素函数的修改
- 五.建堆
-
- 1.自顶向下的建堆方式(利用向上调整算法)
- 2.自底向上的建堆方式(利用向下调整算法)
- 3.两种方法建堆的时间复杂度
-
- 1.向下调整算法建堆的时间复杂度
- 2.向上调整算法建堆的时间复杂度
- 六.堆排序
-
- 1.算法思想
- 2.代码实现
- 3.时间复杂度
- 4.稳定性
- 七.TOP-K问题
- 八.一道与TOP-K相关的leetcode题目
- 九.测试TOP-K对于海量数据的处理
- 十.总结
一.堆的基本知识点
1.知识点
1.堆的知识点:
堆的知识点
堆的逻辑结构是一颗完全二叉树
堆的物理结构是一个数组
也就是说,给我们是一个数组,可是我们要把它想象成一个完全二叉树来做
通过下标父子结点关系
leftchild = parent * 2 + 1;
rightchild = parent * 2 + 2;
parent = (child - 1) / 2;(child可以是左孩子,也可以是右孩子)
堆的两个特性
1.结构性:用数组表示的完全二叉树
2.有序性:任意节点的关键字是其子树所有结点的最大值
3.堆的两种分类
最大堆(MaxHeap):也称为大顶堆(最大值)
最小堆(MinHeap):也称为小顶堆(最小值)
3.大堆:要求树中所有的父亲都大于等于孩子
小堆:要求所有的父亲都小于等于孩子
堆只有两种:大堆,小堆,其余的都不是堆,注意有些选择题常考堆的判别
大堆:堆顶数据是最大的
小堆:堆顶数据是最小的
二.堆的实现
1.堆的结构
上面我们说过,堆的物理结构是一个数组,逻辑结构是一个完全二叉树,所以堆的实际结构类似于顺序表,只不过我们的处理方式类似于二叉树
那么我们就可以用顺序表那样的结构来表示堆了
于是我们可以写出这样的代码
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}HP;
//堆的初始化
void HeapInit(HP* php);
//堆的销毁
void HeapDestroy(HP* php);
//堆的打印
void HeapPrint(HP* php);
//取堆顶数据
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//返回堆的元素大小
int HeapSize(HP* php);
void HeapInit(HP* php)
{
assert(php);
//这里我们将容量初始化为0,当然,初始化为别的一些数值也可以,这里没有强制要求
php->a = NULL;
php->size = php->capacity = 0;
}
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->capacity = php->size = 0;
php->a = NULL;
}
void HeapPrint(HP* php)
{
int i = 0;
for (i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
int HeapSize(HP* php)
{
assert(php);
return php->size;
}
剩下的一些常见的接口:
//堆的插入
void HeapPush(HP* php, HPDataType x);
//堆的删除
void HeapPop(HP* php);
在这里,我们要先说明一下:
1.在堆中插入一个数据后,我们不能改变堆的特性,
即:原来是小堆,插入数据后还是小堆
原来是大堆,插入数据后还是大堆2.我们的删除操作所要删除的值是堆顶元素.
即数组的第一个元素,
删除操作依然不能改变堆的特性
要想实现堆的插入
首先我们需要先学习一个算法:向上调整算法
2.向上调整算法与堆的插入
假设我们现在有一个小堆(所有的父亲都小于他们所对应的孩子)
我们要插入一个元素

向上调整算法整体思路:
child不断向上跟父亲比,如果比父亲小,跟父亲交换,向上迭代
当该节点调整到父亲小于该节点时,或者该节点调整到数组的首元素位置时调整结束
所以我们可以写出这样的代码
//向上调整算法
//[0,child]区间内向上调整
void AdjustUp(HPDataType* a,int child)
{
int parent = (child - 1) / 2;
//终止条件:孩子等于0,大于0就继续调整
//不要拿父亲作为条件,父亲和孩子都等于0的时候,parent = (0-1)/2还是0,死循环了
//while(parent>=0)
while (child > 0)
{
//建小堆if(a[child]
//建大堆if(a[child]>a[parent])
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
其中,向上调整算法的时间复杂度为O(log2(N)),
最多调整高度次,因为是完全二叉树,所以高度约等于O(log2(N))
实现了向上调整算法之后,我们就可以完成插入了
void HeapPush(HP* php, HPDataType x)
{
assert(php);
//扩容
if (php->size == php->capacity)
{
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
//进行扩容
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
if (NULL == tmp)
{
perror("malloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newCapacity;
}
//插入
php->a[php->size] = x;
php->size++;
//向上调整
AdjustUp(php->a, php->size - 1);
}
2.向下调整算法与堆的删除
假设我们现在有一个小堆

向下调整算法整体思路:
前提:根节点的左子树和右子树都是小堆
child为左右孩子中较小者
如果父亲大于child,交换父亲和child,父亲和孩子向上迭代
于是我们可以写出这样的代码
//向下调整算法(小堆)
//[root,n)区间内向下调整
void AdjustDown(HPDataType* a, int root,int n)
{
int parent = root;
int child = 2 * parent + 1;
while (child < n)
{
//建小堆:if(...&& a[child]>a[child+1])
//建大堆:if(...&& a[child]
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
//建小堆:if(a[parent]>a[child])
//建大堆:if(a[parent]
if (a[parent] > a[child])
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
实现了向下调整算法的代码后,我们可以写出删除的代码
其中,向下调整算法的时间复杂度也为O(log2(N)),
最多调整高度次,因为是完全二叉树,所以高度约等于O(log2(N))
//删除堆顶元素
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&(php->a[0]), &(php->a[php->size - 1]));
php->size--;
AdjustDown(php->a, 0, php->size);
}
三.整体代码
Heap.h
#pragma once
#include Heap.c
#include "Heap.h"
//初始化堆
void HeapInit(HP* php)
{
php->a = NULL;
php->capacity = php->size = 0;
}
//销毁堆
void HeapDestory(HP* php)
{
free(php);
php->capacity = php->size = 0;
}
//打印堆
void HeapPrint(HP* php)
{
int i = 0;
for (i = 0; i < php->size; i++)
{
printf("%d ", php->a[i]);
}
printf("\n");
}
void Swap(HPDataType* h1, HPDataType* h2)
{
HPDataType tmp = *h1;
*h1 = *h2;
*h2 = tmp;
}
//向上调整算法
//区间范围:[0,child]
void AdjustUp(HPDataType* a,int child)
{
int parent = (child - 1) / 2;
//终止条件:孩子等于0,大于0就继续调整
//不要拿父亲作为条件,父亲和孩子都等于0的时候,parent = (0-1)/2还是0,死循环了
//while(parent>=0)
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//插入X继续保持堆形态(小堆:父亲小于孩子)
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
//进行扩容
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);
if (NULL == tmp)
{
perror("malloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newCapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1);
}
//向下调整算法(小堆)
//区间范围:[root,n)
void AdjustDown(HPDataType* a, int root,int n)
{
int parent = root;
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
if (a[parent] > a[child])
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
//删除堆顶元素
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&(php->a[0]), &(php->a[php->size - 1]));
php->size--;
AdjustDown(php->a, 0, php->size);
}
//判断是否为空
bool HeapEmpty(HP* php)
{
return php->size == 0;
}
//返回堆顶元素
HPDataType HeapTop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
return php->a[0];
}
//返回堆的元素大小
int HeapSize(HP* php)
{
assert(php);
return php->size;
}
四.利用回调函数避免对向上和向下调整算法的修改
从上面的讲解中,对于向上调整算法和向下调整算法来说,如果想要实现从小堆到大堆的转换,还需要改一下代码,(尽管只需要改一下比较符号即可),
但是那样的话我们就需要再去实现针对于建大堆的向上调整算法和向下调整算法,
而且还需要根据不同需要去调用不同函数,过于麻烦
所以有什么方法可以避免这种修改吗?
在C语言中,我们可以利用回调函数来完成,对于回调函数来说,大家可以看我的这篇博客
征服C语言指针系列(3)
里面有详细的讲解
1.向上调整算法的修改
void AdjustUp(HPDataType* a, int child, int(*cmp_up)(HPDataType* p1, HPDataType* p2))
{
int parent = (child - 1) / 2;
while (child > 0)
{
//小堆:if(a[parent]>a[child])
//也就是说cmp_up(...,...)这个函数返回值为正数,则建的是小堆
//否则,建的是大堆
if (cmp_up(&a[parent], &a[child]) > 0)
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
2.向下调整算法的修改
void AdjustDown(HPDataType* a, int root,int n, int(*cmp_down)(HPDataType* p1, HPDataType* p2))
{
int parent = root;
int child = 2 * parent + 1;
while (child < n)
{
//小堆:if(a[child]>a[child+1])
//也就是说cmp_down(...,...)这个函数返回值为正数,则建的是小堆
//否则,建的是大堆
if (child + 1 < n && cmp_down(&a[child], &a[child + 1]) > 0)
{
child++;
}
//小堆:if(a[parent]>a[child])
//也就是说cmp_down(...,...)这个函数返回值为正数,则建的是小堆
//否则,建的是大堆
if (cmp_down(&a[parent], &a[child]) > 0)
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
函数调用者自行实现两个函数
int cmp_down(HPDataType* p1, HPDataType* p2);
int cmp_up(const HPDataType* p1, const HPDataType* p2);
//使用函数指针来做一个回调函数
cmp_up:向上调整
cmp_down:向下调整
//建小堆(父亲小于孩子)
int cmp_up(const HPDataType* p1, const HPDataType* p2)
{
return *p1 - *p2;
}
//建大堆
int cmp_up(const HPDataType* p1, const HPDataType* p2)
{
return *p2 - *p1;
}
//建小堆:父亲小于孩子
int cmp_down(HPDataType* p1, HPDataType* p2)
{
return *p1 - *p2;
}
//建大堆
int cmp_down(HPDataType* p1, HPDataType* p2)
{
return *p2 - *p1;
}
3.插入元素和删除元素函数的修改
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->capacity == php->size)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
php->a = tmp;
php->capacity = newcapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1, cmp_up);
}
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&(php->a[0]), &(php->a[php->size - 1]));
php->size--;
AdjustDown(php->a, 0, php->size, cmp_down);
}
经过了上面的修改,我们就可以在不改变代码的情况下,实现大堆或者小堆了
五.建堆
上面的代码可以让我们从无到有建立堆
但是如果我们要把一个数组改造成堆,而且不能浪费其他空间,只能在原数组上改造,那该怎么办呢?
这里我们需要建堆
这里以建小堆为例
1.自顶向下的建堆方式(利用向上调整算法)
根据上文可知进行向上调整算法后,数组中[0,child]区间就变为小堆了,所以我们可以用一个for循环来扩展这个区间让这个区间从[0,1]一直扩到[0,n-1]
于是我们可以写出如下代码
for (int i = 1; i < n; i++)
{
AdjustUp(arr, i, cmp_up);
}
2.自底向上的建堆方式(利用向下调整算法)
既然向上调整算法可以建堆,那么向下调整算法呢?
答案是:也可以建堆
我们可以从最后一个非叶子节点往上建堆,先让下面变成小堆,再让上面变成小堆
那么我们该如何求出最后一个非叶子节点呢?
根据堆的特性,我们得出过如下结论:
parent=(child-1)/2;
parent自然是非叶子节点,那么我们只需要求出最后一个parent不就行了吗?
我们又知道最后一个child的下标一定是n-1
所以得出最后一个parent的下标是(n-1-1)/2;
根据上文我们得出向下调整算法可以使得
数组中区间[root,n)范围内变为小堆
那么我们就可以逐步扩大这个范围,让这个范围从[(n-1-1)/2,n)一直扩大到[0,n)
所以我们可以写出如下代码
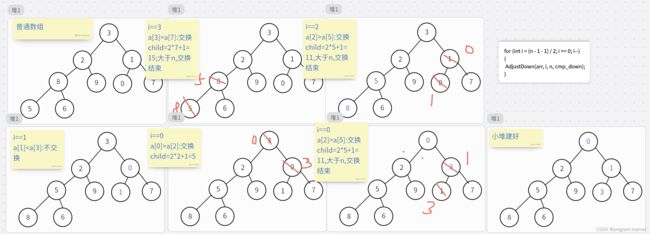
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, n, cmp_down);
}
3.两种方法建堆的时间复杂度
//向下调整算法
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, n, cmp_down);
}
//向上调整算法
for (int i = 1; i < n; i++)
{
AdjustUp(arr, i, cmp_up);
}
可能大家看到这两个代码后的反应是:
因为向上和向下调整算法的时间复杂度都是log(2)N
所以这两种建堆的时间复杂度不都是O(Nlog2(N))吗?
答案是:并不是这样,
向下调整算法建堆的时间复杂度:O(N)
向上调整算法建堆的时间复杂度:O(Nlog(2)N)
下面我们来用数学公式证明一下(这里需要用到错位相减法)
1.向下调整算法建堆的时间复杂度
2.向上调整算法建堆的时间复杂度
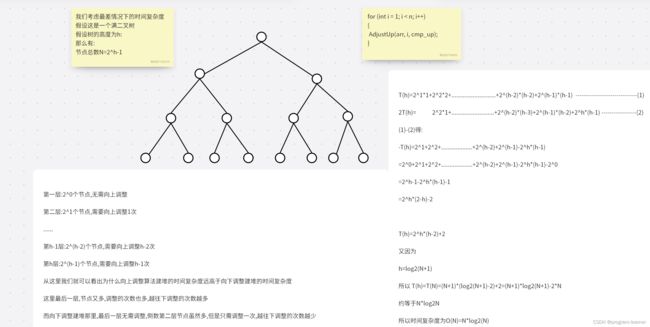
前面已经介绍了如何把一个普通的数组改造成堆
那么接下来我们来看堆的两大重要应用:
堆排序和TOP-K问题
六.堆排序
1.算法思想
1.那么排升序我们要建什么堆呢?
答案是:大堆,这个答案确实挺出人意料的,但是为什么呢?
下面我们来详细解释一下这个原因
1.建小堆为什么不可以(不建议):
2.建大堆为什么可以(建议):
因为:
堆排序是属于选择排序的一种.
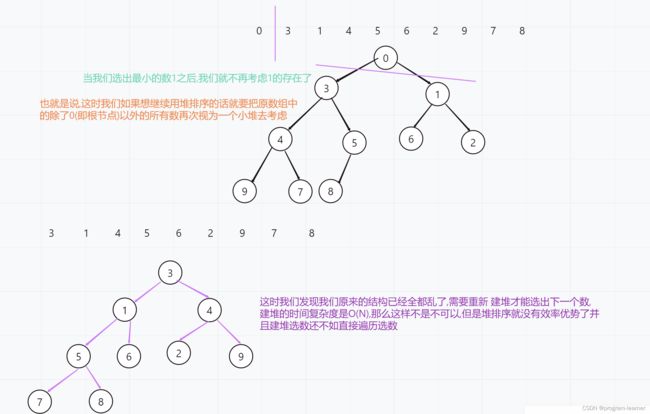
如果是建小堆,最小数在堆顶,已经被选出来了,
那么在剩下的数中再去选数,但是剩下的树结构都乱了,需要重新建堆才能选出下一个数,
建堆的时间复杂度是O(N),我们在讲解堆排序的最后会给大家证明这个建堆的时间复杂度.
那么这样不是不可以,但是堆排序就没有效率优势了并且建堆选数还不如直接遍历选数
其次,如何选次小的数呢?
第二个数去做根了,剩下的树关系全乱了,再重新建堆,
建堆的时间复杂度:O(N),而建堆选数排序,时间复杂度:O(N^2)
并且建堆选数还不如直接遍历选数
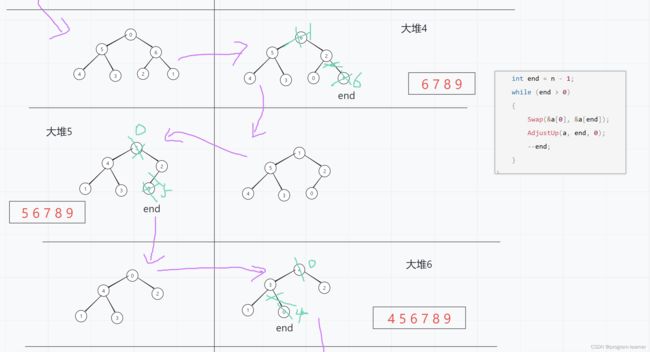
2.建大堆:
步骤:
1.第一个和最后一个交换,然后把交换后的那个较大的数(即位于数组末尾的那个数)不看做堆里面
2.前n-1和数进行向下调整算法,选出次大的数放到根节点,再跟倒数第二个位置交换
2.代码实现
代码如下:
void HeapSort(int* a,int n)
{
int i = 0;
//这里用向下调整算法来建堆,因为时间复杂度只有O(N)
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustUp(a, end, 0);
--end;
}
}
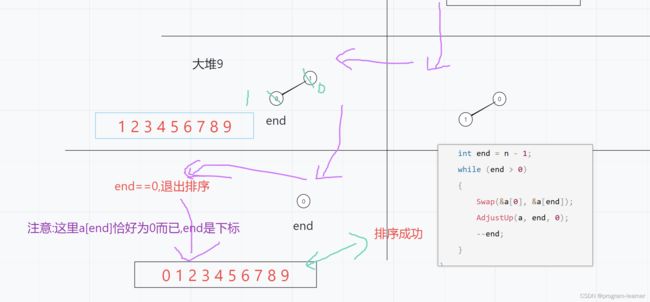
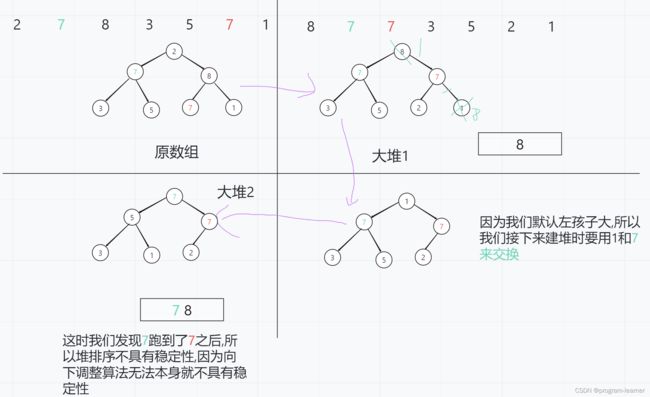
下面给大家画图演示一下,能帮助大家有更好的理解
3.时间复杂度
void HeapSort(int* a,int n)
{
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustUp(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustUp(a, end, 0);
--end;
}
}
向下调整算法最坏的情况:进行高度次,即log(2)N次,所以while循环最坏进行了(n-1)log(2)N次,而for循环的建堆的时间复杂度为O(N)
所以整体的时间复杂度为O(Nlog(2)N)
整个效率相对来说是很高的
4.稳定性
七.TOP-K问题
可能很多小伙伴有这么一个疑问:什么是TOP-K问题啊?
TOP-K问题:
就是求数据集合中前K个最大或者最小的元素,一般情况下数据量都比较大
比如:
全国企业500强,专业前10名,全国高考前100名等等…
那么我们如何利用堆来解决TOP-K问题呢?
假设有10亿个数据,内存存不下,数据在文件中
找出最大的前K个, K==100
1.读取文件的前100个数据,在内存数组中建立一个小堆
2.再依次读取剩下的数据,跟堆顶数据比较,大于堆顶,就替换它进堆,向下调整
3.所有数据读取完毕,堆里面的数据就是最大的前100个
那么我们要建小堆还是大堆呢?
答案是:找最大的前K个就建小堆
反之,建大堆
为什么不建议建大堆:
大堆只能找出最大的一个数,
而且最大的数会挡在根节点的位置,后面的数完全无法进堆,那就完蛋了
小堆的优势
而小堆的话,只有第K个大的数才会挡在根节点的位置,而更大的数会往堆的下面跑
时间复杂度O(N*logK),而且K相对于N来说可以忽略不计,所以可以认为是O(N)
时间复杂度:O(K),K:堆的大小,而K相对于N来说可以忽略不计,所以可以认为是O(1)
下面我们结合一道leetcode题目来实现一下这个代码
八.一道与TOP-K相关的leetcode题目
最小K个数
void Swap(int*p1,int*p2)
{
int tmp =*p1;
*p1 = *p2;
*p2 = tmp;
}
//前k个数建大堆
//向下调整算法
void AdjustDown(int*a,int n,int parent)
{
int minchild = parent*2+1;
while(minchild<n)
{
if(minchild+1<n&&a[minchild+1]>a[minchild])
{
minchild++;
}
if(a[minchild]>a[parent])
{
Swap(&a[minchild],&a[parent]);
parent = minchild;
minchild = parent*2+1;
}
else
{
break;
}
}
}
int* smallestK(int* arr, int arrSize, int k, int* returnSize){
if(k==0)
{
*returnSize=0;
return NULL;
}
int* ret=(int*)malloc(sizeof(int)*k);
for(int i=0;i<k;i++)
{
ret[i]=arr[i];
}
//前k个数建大堆
for(int i=(k-1-1)/2;i>=0;i--)
{
AdjustDown(ret,k,i);
}
for(int i=k;i<arrSize;i++)
{
if(ret[0]>arr[i])
{
ret[0]=arr[i];
AdjustDown(ret,k,0);
}
}
*returnSize=k;
return ret;
}
九.测试TOP-K对于海量数据的处理
下面我们来测试一下TOP-K对于大数据的处理功能
//创建一个文件,并且随机生成一些数字
void CreateDataFile(const char* filename, int N)
{
FILE* Fin = fopen(filename, "w");
if (Fin == NULL)
{
perror("fopen fail");
exit(-1);
}
srand(time(0));
for (int i = 0; i < N; i++)
{
fprintf(Fin, "%d ", rand() % 10000);
}
}
void PrintTopK(const char* filename, int k)
{
assert(filename);
FILE* fout = fopen(filename, "r");
if (fout == NULL)
{
perror("fopen fail");
return;
}
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror("malloc fail");
return;
}
//读前k个数
for (int i = 0; i < k; i++)
{
//空格和换行默认是多个值之间的间隔
fscanf(fout, "%d", &minheap[i]);
}
//建k个数的堆
for (int j = (k - 1 - 1) / 2; j >= 0; j--)
{
AdjustDown(minheap, j, k, cmp_down);
}
//读取后N-K个
int x = 0;
while(fscanf(fout,"%d",&x)!=EOF)
{
if (x > minheap[0])
{
minheap[0] = x;
AdjustDown(minheap, 0, k, cmp_down);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
printf("\n");
free(minheap);
fclose(fout);
}
int main()
{
//CreateDataFile("data.txt", 1000000);
//找前10个最大的数
PrintTopK("data.txt", 10);
return 0;
}
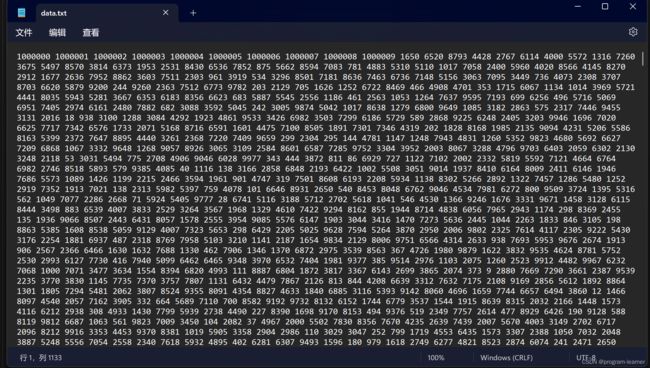
我们已经提前修改了文件当中的值,
现在文件当中的最大的前10个值是1000000到1000009
运行后的结果:

可见堆针对于TOP-K的强大之处
十.总结
本文介绍了
1.堆的知识点
2.用C语言实现了堆
3.并且用函数指针实现了回调函数对向上和向下调整算法的代码进行了优化
4.实现了建堆
5.用数学公式推导出了两种建堆方法的时间复杂度
6.实现了堆排序
7.分析了堆排序的时间复杂度和稳定性
8.介绍了TOP-K的代码实现并解决了一道leetcode题目
9.测试了TOP-K对于大数据的处理功能
以上就是<<数据结构-堆的实现及应用>>的讲解,希望能对大家有所帮助,谢谢大家!