LeetCode 807. 保持城市天际线 / 630. 课程表 III(贪心+优先队列)/ 851. 喧闹和富有(拓扑排序)
807. 保持城市天际线
2021.12.13 每日一题
题目描述
给你一座由 n x n 个街区组成的城市,每个街区都包含一座立方体建筑。给你一个下标从 0 开始的 n x n 整数矩阵 grid ,其中 grid[r][c] 表示坐落于 r 行 c 列的建筑物的 高度 。
城市的 天际线 是从远处观察城市时,所有建筑物形成的外部轮廓。从东、南、西、北四个主要方向观测到的 天际线 可能不同。
我们被允许为 任意数量的建筑物 的高度增加 任意增量(不同建筑物的增量可能不同) 。 高度为 0 的建筑物的高度也可以增加。然而,增加的建筑物高度 不能影响 从任何主要方向观察城市得到的 天际线 。
在 不改变 从任何主要方向观测到的城市 天际线 的前提下,返回建筑物可以增加的 最大高度增量总和 。
示例 1:
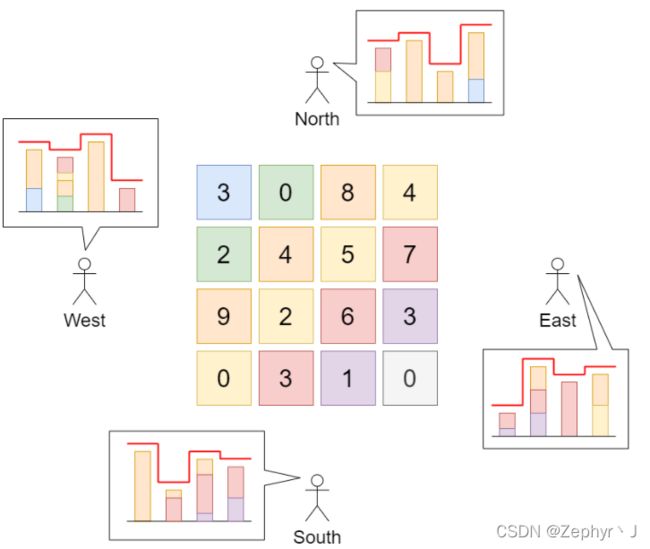
输入:grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
输出:35
解释:建筑物的高度如上图中心所示。
用红色绘制从不同方向观看得到的天际线。
在不影响天际线的情况下,增加建筑物的高度:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]
示例 2:
输入:grid = [[0,0,0],[0,0,0],[0,0,0]]
输出:0
解释:增加任何建筑物的高度都会导致天际线的变化。
提示:
n == grid.length
n == grid[r].length
2 <= n <= 50
0 <= grid[r][c] <= 100
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/max-increase-to-keep-city-skyline
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
class Solution {
public int maxIncreaseKeepingSkyline(int[][] grid) {
//每一个位置的最大高度就是横竖两个方向最低的高度
//因为那是天际线
int n = grid.length;
int[] col = new int[n];
int[] row = new int[n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
col[i] = Math.max(col[i], grid[i][j]);
row[j] = Math.max(row[j], grid[i][j]);
}
}
int res = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
int temp = Math.min(col[i], row[j]);
res += temp - grid[i][j];
}
}
return res;
}
}
630. 课程表 III
2021.12.14 每日一题
题目描述
这里有 n 门不同的在线课程,按从 1 到 n 编号。给你一个数组 courses ,其中 courses[i] = [durationi, lastDayi] 表示第 i 门课将会 持续 上 durationi 天课,并且必须在不晚于 lastDayi 的时候完成。
你的学期从第 1 天开始。且不能同时修读两门及两门以上的课程。
返回你最多可以修读的课程数目。
示例 1:
输入:courses = [[100, 200], [200, 1300], [1000, 1250], [2000, 3200]]
输出:3
解释:
这里一共有 4 门课程,但是你最多可以修 3 门:
首先,修第 1 门课,耗费 100 天,在第 100 天完成,在第 101 天开始下门课。
第二,修第 3 门课,耗费 1000 天,在第 1100 天完成,在第 1101 天开始下门课程。
第三,修第 2 门课,耗时 200 天,在第 1300 天完成。
第 4 门课现在不能修,因为将会在第 3300 天完成它,这已经超出了关闭日期。
示例 2:
输入:courses = [[1,2]]
输出:1
示例 3:
输入:courses = [[3,2],[4,3]]
输出:0
提示:
1 <= courses.length <= 10^4
1 <= durationi, lastDayi <= 10^4
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/course-schedule-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
class Solution {
public int scheduleCourse(int[][] courses) {
//范围是10的4次,应该是个拓扑排序我觉得
//按照截止日期排序还是按照花费时间排序呢
//如果按照截止日期排序的话,每次取出来是截止日期最早的,但是不是时间最短的,这样会有问题吗
//应该是会有问题的,比如后面有几个时间很短的,就不能被完成
//首先明确第一点,两门课程,有截止时间d1<=d2,那么先完成课程1再完成课程2肯定比反过来是更优的
//这是必然呢,因为想一下,如果能先学习后面的,再学习前面的,那么肯定可以先学习前面的,再学习后面的,而反过来就不一定了
//所以将所有课程按照截止时间排序,依次选出课程
//如果当前选出了一个最优的课程序列,k1,k2..kn,判断下一个课程是否可以加入这个序列
//如果这个课程满足截止时间的要求,那么可以加入,并且因为之前序列是最优的,所以加入也是最优的
//如果这个课程不满足截止时间的要求,那么就看这个课程能否替换原来序列的课程
//如果原来序列中的课程时间都比这个课程短,那么不能替换;如果有一个比这个长,那么就可以进行替换
int n = courses.length;
//按照截止时间排序
Arrays.sort(courses, (a, b) -> (a[1] - b[1]));
//用一个优先队列记录目前序列中的课程所需时间,替换堆顶的课程
PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> (b - a));
int time = 0;
for(int i = 0; i < n; i++){
int temptime = time + courses[i][0];
//如果可以加入,那么插入最后
if(temptime <= courses[i][1]){
pq.offer(courses[i][0]);
time = temptime;
}else{
//如果不可以,那么替换
if(!pq.isEmpty() && pq.peek() > courses[i][0]){
int t = pq.poll();
pq.offer(courses[i][0]);
time = time - t + courses[i][0];
}
}
}
return pq.size();
}
}
851. 喧闹和富有
2021.12.15 每日一题
题目描述
有一组 n 个人作为实验对象,从 0 到 n - 1 编号,其中每个人都有不同数目的钱,以及不同程度的安静值(quietness)。为了方便起见,我们将编号为 x 的人简称为 "person x "。
给你一个数组 richer ,其中 richer[i] = [ai, bi] 表示 person ai 比 person bi 更有钱。另给你一个整数数组 quiet ,其中 quiet[i] 是 person i 的安静值。richer 中所给出的数据 逻辑自恰(也就是说,在 person x 比 person y 更有钱的同时,不会出现 person y 比 person x 更有钱的情况 )。
现在,返回一个整数数组 answer 作为答案,其中 answer[x] = y 的前提是,在所有拥有的钱肯定不少于 person x 的人中,person y 是最安静的人(也就是安静值 quiet[y] 最小的人)。
示例 1:
输入:richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]], quiet = [3,2,5,4,6,1,7,0]
输出:[5,5,2,5,4,5,6,7]
解释:
answer[0] = 5,
person 5 比 person 3 有更多的钱,person 3 比 person 1 有更多的钱,person 1 比 person 0 有更多的钱。
唯一较为安静(有较低的安静值 quiet[x])的人是 person 7,
但是目前还不清楚他是否比 person 0 更有钱。
answer[7] = 7,
在所有拥有的钱肯定不少于 person 7 的人中(这可能包括 person 3,4,5,6 以及 7),
最安静(有较低安静值 quiet[x])的人是 person 7。
其他的答案也可以用类似的推理来解释。
示例 2:
输入:richer = [], quiet = [0]
输出:[0]
提示:
n == quiet.length
1 <= n <= 500
0 <= quiet[i] < n
quiet 的所有值 互不相同
0 <= richer.length <= n * (n - 1) / 2
0 <= ai, bi < n
ai != bi
richer 中的所有数对 互不相同
对 richer 的观察在逻辑上是一致的
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/loud-and-rich
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这样写竟然超时了,相当于一个拓扑排序
因为是计算每个人的时候,都进行了一次图的遍历,其实做了很多无用功,应该是在一次遍历的时候,如果遇到了能计算的,就直接计算出结果,后面就不用再遍历一次这个值了
这样应该能快很多,想想怎么写
class Solution {
public int[] loudAndRich(int[][] richer, int[] quiet) {
//两个比较的维度,一个是富有,一个是安静
//需要先将两个维度进行排序,对于安静值,比如说查一群人中安静值最小的人,
//首先得找到这群人,然后直接在quiet数组中比较这群人的安静值就行了
//那么怎么找这群人呢,就是根据richer给出的关系,可以构建一幅图,然后根据这幅图的关系来查找答案
//怎么构造这幅图比较方便呢,因为是单向的,所以可以构建一个二维数组
//g[i][j]为true表示i比j有钱,或者就直接遍历richer数组
//比如判断0位置,那么
int n = quiet.length;
int l = richer.length;
//统计比key直接富有的人
Map<Integer, List<Integer>> map = new HashMap<>();
for(int i = 0; i < l; i++){
int rich = richer[i][0];
int poor = richer[i][1];
List<Integer> list = map.getOrDefault(poor, new ArrayList<>());
list.add(rich);
map.put(poor, list);
}
int[] res = new int[n];
for(int i = 0; i < n; i++){
//如果没有这个人的关系
if(!map.containsKey(i)){
res[i] = i;
continue;
}
List<Integer> list = map.get(i);
Queue<Integer> queue = new LinkedList<>();
for(int p : list){
queue.add(p);
}
int min = quiet[i]; //最小的安静值
int minp = i;
while(!queue.isEmpty()){
//当前人
int p = queue.poll();
//如果比当前富有的人的安静值小于当前人的安静值,那么替换
if(quiet[p] < min){
min = quiet[p];
minp = p;
}
List<Integer> temp = map.getOrDefault(p, new ArrayList<>());
for(int peo : temp){
queue.add(peo);
}
}
res[i] = minp;
}
return res;
}
}
改成递归形式,做一次处理,过了
class Solution {
Map<Integer, List<Integer>> map;
int[] quiet;
int[] res;
public int[] loudAndRich(int[][] richer, int[] quiet) {
//两个比较的维度,一个是富有,一个是安静
//需要先将两个维度进行排序,对于安静值,比如说查一群人中安静值最小的人,
//首先得找到这群人,然后直接在quiet数组中比较这群人的安静值就行了
//那么怎么找这群人呢,就是根据richer给出的关系,可以构建一幅图,然后根据这幅图的关系来查找答案
//怎么构造这幅图比较方便呢,因为是单向的,所以可以构建一个二维数组
//g[i][j]为true表示i比j有钱,或者就直接遍历richer数组
//比如判断0位置,那么
this.quiet = quiet;
int n = quiet.length;
int l = richer.length;
//统计比key直接富有的人
map = new HashMap<>();
for(int i = 0; i < l; i++){
int rich = richer[i][0];
int poor = richer[i][1];
List<Integer> list = map.getOrDefault(poor, new ArrayList<>());
list.add(rich);
map.put(poor, list);
}
res = new int[n];
Arrays.fill(res, -1);
for(int i = 0; i < n; i++){
if(res[i] == -1)
backtracking(i);
}
return res;
}
public int backtracking(int i){
//如果没有这个人的关系
if(!map.containsKey(i)){
res[i] = i;
return i;
}
int min = quiet[i];
int minp = i;
List<Integer> list = map.get(i);
for(int p : list){
//如果这个人已经得到了结果了
int temp = -1;
if(res[p] != -1){
temp = res[p];
//否则递归
}else
temp = backtracking(p);
if(quiet[temp] < min){
min = quiet[temp];
minp = temp;
}
}
res[i] = minp;
return minp;
}
}
将图反过来,可以用拓扑排序一次遍历完成
class Solution {
public int[] loudAndRich(int[][] richer, int[] quiet) {
//写一下一次的拓扑排序
int n = quiet.length;
int l = richer.length;
boolean[][] g = new boolean[n][n]; //富有指向贫穷
int[] inDeg = new int[n]; //入度
for(int i = 0; i < l; i++){
g[richer[i][0]][richer[i][1]] = true;
inDeg[richer[i][1]]++;
}
Queue<Integer> queue = new LinkedList<>();
int[] res = new int[n];
for(int i = 0; i < n; i++){
res[i] = i;
if(inDeg[i] == 0)
queue.add(i);
}
while(!queue.isEmpty()){
int top = queue.poll();
//遍历所有比它贫穷的人
for(int i = 0; i < n; i++){
if(g[top][i]){
//如果当前富有的这个人的安静值比穷的人安静值小,那么更改
if(quiet[res[top]] < quiet[res[i]])
res[i] = res[top];
//这个人的入度减1
inDeg[i]--;
if(inDeg[i] == 0)
queue.add(i);
}
}
}
return res;
}
}