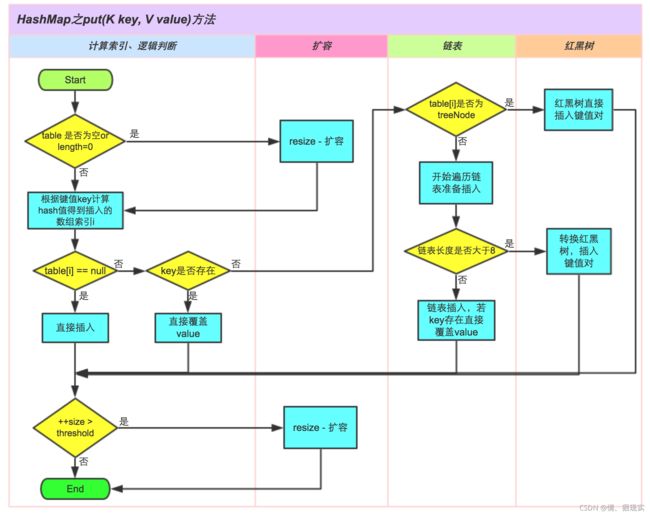
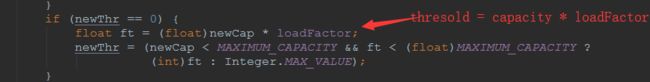Java集合 HashMap 源码分析

HashMap

介绍

HashMap是Map接口使用频率最高的实现类
HashMap是以key-val对的方式来存储数据（HashMap$Node)
key不能重复，但是值可以重复，允许使用null键和null值
如果添加相同的key，则会覆盖原来的key-val，等同于修改（key不会替换，val会替换）
与HashSet一样不保证映射的顺序，因为底层是以hash表的方式来存储的(jdk8 数组+链表+红黑树)
HashMap没有实现同步，线程不安全（线程安全的是ConcurrentHashMap）
扩容是一个特别耗性能的操作，所以当程序员在使用HashMap的时候，估算map的大小，初始化的时候给一个大致的数值，避免map进行频繁的扩容。
负载因子是可以修改的，也可以大于1，但是建议不要轻易修改，除非情况非常特殊。

扩容机制

HashMap底层维护了Node类型的数组table，默认为null
当创建对象时，将加载因子（loadfactor）初始化为0.75
当添加key-val时，通过key的哈希值得到在table的索引，然后判断该索引处是否有元素，如果没有元素则直接添加，如果有元素，继续判断该元素的key是否和准备加入的key相等，如果相等则直接替换val，如果不相等则需要判断是树结构还是链表结果，做出相应处理，如果添加时发现容量不够，则需要扩容
第一次添加，则需要扩容table容量为16，临界值（threshold）为12；(16*0.75=12)
以后的扩容，则需要扩容table的容量为原来的2倍，临界值为原来的2倍，依次类推

在Java8中，如果一条链表的元素个数超过TREEIFY_THRESHOLD(默认8)，并且table大小>=MIN_TREEIFY_CAPACITY(默认64)，就会进行树化(红黑树)

Node<K,V> e; K k;
if (p.hash == hash &&//这里判断了链表的头节点
    ((k = p.key) == key || (key != null && key.equals(k))))
    e = p;
else if (p instanceof TreeNode)
    e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
    //binCount从0开始 然而之前已经比较过头结点 所以实际从第二个节点开始比较
    //binCount=0->第2个 
    //binCount >= TREEIFY_THRESHOLD - 1 即 binCount >= 7   [TREEIFY_THRESHOLD默认为8]
    //当binCount = 7 时 此时为第9个 才调用 treeifyBin()
    //结论 一条链表长度超过8个 才会调用treeifyBin()
    for (int binCount = 0; ; ++binCount) {
        if ((e = p.next) == null) {
            p.next = newNode(hash, key, value, null);
            if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                treeifyBin(tab, hash);
            break;
        }
        if (e.hash == hash &&
            ((k = e.key) == key || (key != null && key.equals(k))))
            break;
        p = e;
    }
}
if (e != null) { // existing mapping for key
    V oldValue = e.value;
    if (!onlyIfAbsent || oldValue == null)
        e.value = value;
    afterNodeAccess(e);
    return oldValue;
}

treefiBin()当table容量达到64才会树化否则调用 resize()扩容

final void treeifyBin(Node<K,V>[] tab, int hash) {
    int n, index; Node<K,V> e;
    //如果table为空或者容量小于64 [MIN_TREEIFY_CAOACITY默认为64]
    //则调用resize()扩容
    //否则进行树化（红黑树）
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        resize();
    else if ((e = tab[index = (n - 1) & hash]) != null) {
        TreeNode<K,V> hd = null, tl = null;
        do {
            TreeNode<K,V> p = replacementTreeNode(e, null);
            if (tl == null)
                hd = p;
            else {
                p.prev = tl;
                tl.next = p;
            }
            tl = p;
        } while ((e = e.next) != null);
        if ((tab[index] = hd) != null)
            hd.treeify(tab);
    }
}

untreeify()解除树化变回链表节点数小于等于6则变回链表

//lc 树的节点个数 UNTREEIFY_THRESHOLD（默认6）
//节点数 <= 6 则变回链表
if (lc <= UNTREEIFY_THRESHOLD)
    tab[index] = loHead.untreeify(map);

构造方法

`HashMap()` 构造一个空的 `HashMap` ，默认初始容量（16）和默认负载系数（0.75）。
`HashMap(int initialCapacity)` 构造一个空的 `HashMap`具有指定的初始容量和默认负载因子（0.75）。
`HashMap(int initialCapacity, float loadFactor)` 构造一个空的 `HashMap`具有指定的初始容量和负载因子。
`HashMap(Map m)` 构造一个新的 `HashMap`与指定的相同的映射 `Map` 。

方法

`void`	`clear()` 从这张Map中删除所有的映射。
`Object`	`clone()` 返回此 `HashMap`实例的浅拷贝：键和值本身不被克隆。
`V`	`compute(K key, BiFunction remappingFunction)` 尝试计算用于指定键和其当前映射的值的映射（或 `null`如果没有当前映射）。
`V`	`computeIfAbsent(K key, Function mappingFunction)` 如果指定的键尚未与值相关联（或映射到 `null` ），则尝试使用给定的映射函数计算其值，并将其输入到此映射中，除非 `null` 。
`V`	`computeIfPresent(K key, BiFunction remappingFunction)` 如果指定的密钥的值存在且非空，则尝试计算给定密钥及其当前映射值的新映射。
`boolean`	`containsKey(Object key)` 如果此映射包含指定键的映射，则返回 `true` 。
`boolean`	`containsValue(Object value)` 如果此Map将一个或多个键映射到指定值，则返回 `true` 。
`Set>`	`entrySet()` 返回此Map中包含的映射的`Set`视图。
`void`	`forEach(BiConsumer action)` 对此映射中的每个条目执行给定的操作，直到所有条目都被处理或操作引发异常。
`V`	`get(Object key)` 返回到指定键所映射的值，或 `null`如果此映射包含该键的映射。
`V`	`getOrDefault(Object key, V defaultValue)` 返回到指定键所映射的值，或 `defaultValue`如果此映射包含该键的映射。
`boolean`	`isEmpty()` 如果此Map不包含键值映射，则返回 `true` 。
`Set`	`keySet()` 返回此Map中包含的键的`Set`视图。
`V`	`merge(K key, V value, BiFunction remappingFunction)` 如果指定的键尚未与值相关联或与null相关联，则将其与给定的非空值相关联。
`V`	`put(K key, V value)` 将指定的值与此映射中的指定键相关联。
`void`	`putAll(Map m)` 将指定Map的所有映射复制到此Map。
`V`	`putIfAbsent(K key, V value)` 如果指定的键尚未与某个值相关联（或映射到 `null` ），则将其与给定值相关联并返回 `null` ，否则返回当前值。
`V`	`remove(Object key)` 从该Map中删除指定键的映射（如果存在）。
`boolean`	`remove(Object key, Object value)` 仅当指定的密钥当前映射到指定的值时删除该条目。
`V`	`replace(K key, V value)` 只有当目标映射到某个值时，才能替换指定键的条目。
`boolean`	`replace(K key, V oldValue, V newValue)` 仅当当前映射到指定的值时，才能替换指定键的条目。
`void`	`replaceAll(BiFunction function)` 将每个条目的值替换为对该条目调用给定函数的结果，直到所有条目都被处理或该函数抛出异常。
`int`	`size()` 返回此Map中键值映射的数量。
`Collection`	`values()` 返回此Map中包含的值的`Collection`视图。

内部基本属性常量

/**
 * 默认初始容量—必须是2的幂。
 * 为啥不直接写16？？
 */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16：

/**
 * 最大容量，如果较高的值由带参数的任何构造函数隐式指定，则使用该值。必须是2的幂 <= 1<<30。
 */
static final int MAXIMUM_CAPACITY = 1 << 30;

/**
 * 构造函数中没有指定时使用的负载因子。
 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;

/**
 * 使用树(而不是列表)来设置桶的计数阈值。当向至少具有这么多节点的桶添加元素时，桶将转换为树。
 * 该值必须大于2，并且应该至少为8，以便与树木移除中关于收缩后转换回普通桶的假设相吻合。
 * 为啥不是 1 << 3 ?
 */
static final int TREEIFY_THRESHOLD = 8;

/**
 * 用于在调整大小操作期间反树化(拆分)桶的计数阈值。
 * 应小于TREEIFY_THRESHOLD，且最多6个以配合收缩检测下删除。
 */
static final int UNTREEIFY_THRESHOLD = 6;

/**
 * 最小的表容量，其中的桶可以树化。(否则，如果一个桶中有太多节点，则会调整表的大小。)
 * 应至少为4 * TREEIFY_THRESHOLD，以避免调整大小和treeification阈值之间的冲突。
 */
static final int MIN_TREEIFY_CAPACITY = 64;


/**
 * 表，第一次使用时初始化，并根据需要调整大小。当分配时，长度总是2的幂。
 * (在某些操作中，我们还允许长度为零，以允许当前不需要的引导机制。)
 */
transient Node<K, V>[] table;

/**
 * 保存缓存entrySet ()。AbstractMap字段用于keySet()和values()。
 */
transient Set<Entry<K, V>> entrySet;

/**
 * 此映射中包含的键值映射的数目。
 */
transient int size;

/**
 * 这个HashMap在结构上被修改的次数，结构修改是指改变HashMap中映射的数量或修改其内部结构的次数(例如，rehash)。
 * 此字段用于使HashMap集合视图上的迭代器快速失效。(见ConcurrentModificationException)。
 */
transient int modCount;

/**
 * 要调整大小的下一个大小值=(capacity * load factor)
 */
int threshold;

/**
 * 哈希表的加载因子
 */
final float loadFactor;

hash计算:

1、通过hashCode()的高16位异或低16位实现的：( h=k.hashCode())^(h>>>16))，主要是从速度、功效、质量来考虑的，这么做可以在数组table的length比较小的时候，也能保证考虑到高低Bit都参与到Hash的计算中，同时不会有太大的开销。

2、计算组数下标：h&(table.length-1)，HashMap底层数组的长度总是2的n次方，这是HashMap在速度上的优。当length总是2的n次方时，h&(length-1)运算等价于对length取模，也就是h%length，但是&比％具有更高的效率。

put

如果已经存在则覆盖且返回原value，否则返回null
put过程:

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

// 第三个参数 onlyIfAbsent 如果是 true，那么只有在不存在该 key 时才会进行 put 操作
// 第四个参数 evict 我们这里不关心
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    // 第一次 put 值的时候，会触发下面的 resize()，类似 java7 的第一次 put 也要初始化数组长度
    // 第一次 resize 和后续的扩容有些不一样，因为这次是数组从 null 初始化到默认的 16 或自定义的初始容量
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    // 找到具体的数组下标，如果此位置没有值，那么直接初始化一下 Node 并放置在这个位置就可以了
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);

    else {// 数组该位置有数据
        Node<K,V> e; K k;
        // 首先，判断该位置的第一个数据和我们要插入的数据，key 是不是"相等"，如果是，取出这个节点
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        // 如果该节点是代表红黑树的节点，调用红黑树的插值方法，本文不展开说红黑树
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        else {
            // 到这里，说明数组该位置上是一个链表
            for (int binCount = 0; ; ++binCount) {
                // 插入到链表的最后面(Java7 是插入到链表的最前面)
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);
                    // TREEIFY_THRESHOLD 为 8，所以，如果新插入的值是链表中的第 8 个
                    // 会触发下面的 treeifyBin，也就是将链表转换为红黑树
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }
                // 如果在该链表中找到了"相等"的 key(== 或 equals)
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    // 此时 break，那么 e 为链表中[与要插入的新值的 key "相等"]的 node
                    break;
                p = e;
            }
        }
        // e!=null 说明存在旧值的key与要插入的key"相等"
        // 对于我们分析的put操作，下面这个 if 其实就是进行 "值覆盖"，然后返回旧值
        if (e != null) {
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;
    // 如果 HashMap 由于新插入这个值导致 size 已经超过了阈值，需要进行扩容
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

get

1、计算 key 的 hash 值，根据 hash 值找到对应数组下标: hash & (length-1)

2、判断数组该位置处的元素是否刚好就是我们要找的，如果不是，走第三步

3、判断该元素类型是否是 TreeNode，如果是，用红黑树的方法取数据，如果不是，走第四步

4、遍历链表，直到找到相等(==或equals)的 key

public V get(Object key) {
    //当前节点
    Node<K, V> e;
    //获取当前节点，并返回节点的值
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}

final Node<K, V> getNode(int hash, Object key) {
    //当前表
    Node<K, V>[] tab;
    Node<K, V> first, e;
    int n;
    K k;
    //如果当前表不为null,且表长度大于0.并且找到桶的位置
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
        //如果第一个就和key相等
        if (first.hash == hash && // always check first node
            ((k = first.key) == key || (key != null && key.equals(k))))
            //返回桶的第一个元素
            return first;
        //如果第一个节点后面还有接待你
        if ((e = first.next) != null) {
            //如果是红黑树
            if (first instanceof TreeNode)
                //获取树中的节点
                return ((TreeNode<K, V>) first).getTreeNode(hash, key);
            //迭代链表，获取匹配的节点
            do {
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    //没找到，返回null
    return null;
}

thresold、loadFactor

当 HashMap 中的 size >= threshold 时，HashMap 就要扩容。

size：HashMap表中包含的键值映射的数目。
threshold：要调整大小的下一个大小的阈值，等于(capacity * loadFactor)。
capacity：HashMap容量
loadFactor：哈希表的加载因子。

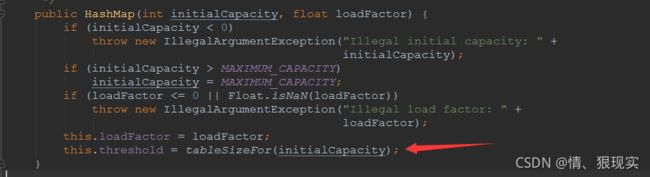
其中有一个tableSizeFor()方法的作用是： 找到>=这个值的一个2的次方数。

这个方法是在计算阈值thresold的时候调用的 (初始计算threshold的时候):

举例:

public class Main {
    public static void main(String[] args) {
        for(int i = 0; i < 35; i++){
            System.out.println(i + " -> " + tableSizeFor(i));
        }
    }

    static final int MAXIMUM_CAPACITY = 1 << 30;

    static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }
}

输出:

0 -> 1
1 -> 1
2 -> 2
3 -> 4
4 -> 4
5 -> 8
6 -> 8
7 -> 8
8 -> 8
9 -> 16
10 -> 16
11 -> 16
12 -> 16
13 -> 16
14 -> 16
15 -> 16
16 -> 16
17 -> 32
18 -> 32
19 -> 32
20 -> 32
21 -> 32
22 -> 32
23 -> 32
24 -> 32
25 -> 32
26 -> 32
27 -> 32
28 -> 32
29 -> 32
30 -> 32
31 -> 32
32 -> 32
33 -> 64
34 -> 64

添加第一个元素时，默认分配的大小为16，不过，并不是size大于16时再进行扩展，下次什么时候扩展与threshold有关。

threshold表示阈值，当键值对个数size大于等于threshold时考虑进行扩展。threshold是怎么算出来的呢？初始阈值就是上面的tableSizeFor()方法计算得到，也就是和initCapity有关。

后面一般而言，threshold等于table.length乘以loadFactor，比如，如果table.length为16，loadFactor为0.75，则threshold为12，看下面的源码。

loadFactor是负载因子，表示整体上table被占用的程度，是一个浮点数，默认为0.75，可以通过构造方法进行修改。

HashMap 红黑树

原博客：https://www.cnblogs.com/mfrank/p/9227097.html

红黑树介绍

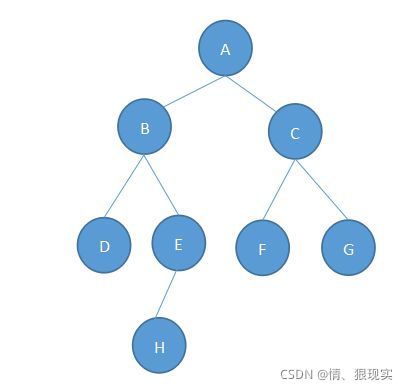
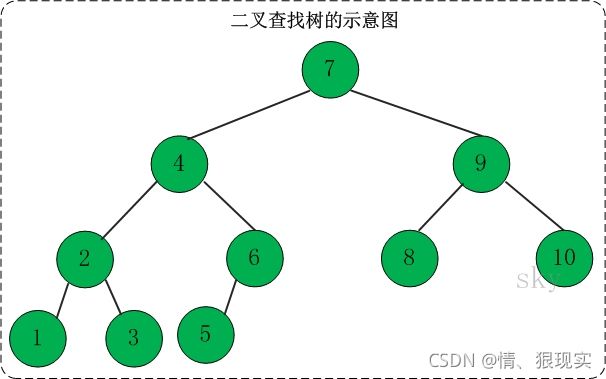
什么是红黑树？嗯，首先，它是一颗树，所谓的树，便是长的像这样的东西

不像树？emmmm，你把它想象成一颗倒过来的树就好了，A~H都是树的节点，每个节点有零个或者多个子节点，或者说多个孩子，但除了根节点以外，每个节点都只有一个父节点，也称只有一个父亲拿出来，则又是一颗树，称为树的子树。

好了，知道树是什么东西了，那么红黑树是什么样的呢？

红黑树，本质上来说是一颗二叉搜索树。嗯，还是先说说这个二叉搜索树吧。二叉代表它的节点最多有两个子节点，而且左右有顺序，不能颠倒，分别叫左孩子和右孩子，这两个节点互为兄弟节点，嗯，其实叫法根现实里的叫法差不多，以下图为例，4、9互为兄弟，7是他们的父亲，9是2的叔叔，8是2的堂兄弟，很简单吧。说完了称谓，再来说说用途，既然叫做搜索树表示它的用途是为了更快的搜索和查找而设计的，所以这棵树本身满足一定的排序规则，即树中的任何节点的值大于它的左孩子，且小于它的右孩子。任意节点的左、右子树也分别为二叉查找树。嗯，结合下图意会一下：

而红黑树，就跟它的名字一样，又红又黑，红黑并进，理实交融，节点是非红即黑的，看起来就像这样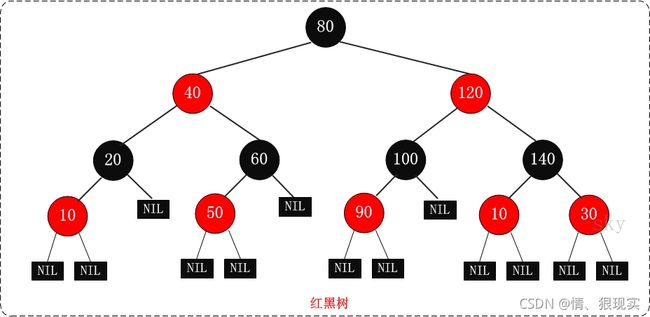

红黑树的主要特性:
　　（1）每个节点要么是黑色，要么是红色。（节点非黑即红）
　　（2）根节点是黑色。
　　（3）每个叶子节点（NIL）是黑色。
　　（4）如果一个节点是红色的，则它的子节点必须是黑色的。（也就是说父子节点不能同时为红色）
　　（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。（这一点是平衡的关键）

说简单也简单，其实就是一颗比较平衡的又红又黑的二叉树嘛。

TreeNode结构

既然我们已经知道红黑树长什么样了，那么我们再来看看HashMap中的TreeNode代码里是如何表示的：

    /**
     * 用于Tree bins 的Entry。 扩展LinkedHashMap.Entry（进而扩展Node），因此可以用作常规节点或链接节点的扩展。
     */
    static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
        TreeNode<K,V> parent;  // 红黑树父节点
        TreeNode<K,V> left;
        TreeNode<K,V> right;
        TreeNode<K,V> prev;    // 删除后需要取消链接
        boolean red;
        TreeNode(int hash, K key, V val, Node<K,V> next) {
            super(hash, key, val, next);
        }　　　　 //省略后续代码

TreeNode继承自LinkedHashMap中的内部类——LinkedHashMap.Entry，而这个内部类又继承自Node，所以算是Node的孙子辈了。我们再来看看它的几个属性，parent用来指向它的父节点，left指向左孩子，right指向右孩子，prev则指向前一个节点（原链表中的前一个节点），注意，这些字段跟Entry，Node中的字段一样，是使用默认访问权限的，所以子类可以直接使用父类的属性。

树化的过程

在前几篇中已经有所介绍，当HashMap桶中的元素个数超过一定数量时，就会树化，也就是将链表转化为红黑树的结构。

    public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
    }

    final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        ...省略部分代码...
            else {
                for (int binCount = 0; ; ++binCount) {
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        //当桶中元素个数超过阈值（8）时就进行树化
                        if (binCount >= TREEIFY_THRESHOLD - 1)
                            treeifyBin(tab, hash);
                        break;
                    }
         ...省略部分代码...
    }

    final void treeifyBin(Node<K,V>[] tab, int hash) {
        int n, index; Node<K,V> e;
        if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
            resize();
        else if ((e = tab[index = (n - 1) & hash]) != null) {
            TreeNode<K,V> hd = null, tl = null;
            do {
                //将节点替换为TreeNode
                TreeNode<K,V> p = replacementTreeNode(e, null);
                if (tl == null)　　　　　　　　　　　　//hd指向头结点
                    hd = p;
                else {
                    //这里其实是将单链表转化成了双向链表，tl是p的前驱，每次循环更新指向双链表的最后一个元素，用来和p相连，p是当前节点
                    p.prev = tl;
                    tl.next = p;
                }
                tl = p;
            } while ((e = e.next) != null);
            if ((tab[index] = hd) != null)
                //将链表进行树化
                hd.treeify(tab);
        }
    }

从代码中可以看到，在treeifyBin函数中，先将所有节点替换为TreeNode，然后再将单链表转为双链表，方便之后的遍历和移动操作。而最终的操作，实际上是调用TreeNode的方法treeify进行的。

final void treeify(Node<K,V>[] tab) {
            //树的根节点
            TreeNode<K,V> root = null;
            //x是当前节点，next是后继
            for (TreeNode<K,V> x = this, next; x != null; x = next) {
                next = (TreeNode<K,V>)x.next;
                x.left = x.right = null;
                //如果根节点为null，把当前节点设置为根节点
                if (root == null) {
                    x.parent = null;
                    x.red = false;
                    root = x;
                }
                else {
                    K k = x.key;
                    int h = x.hash;
                    Class<?> kc = null;
                    //这里循环遍历，进行二叉搜索树的插入
                    for (TreeNode<K,V> p = root;;) {
                        //p指向遍历中的当前节点，x为待插入节点，k是x的key，h是x的hash值，ph是p的hash值，dir用来指示x节点与p的比较，-1表示比p小，1表示比p大，不存在相等情况，因为HashMap中是不存在两个key完全一致的情况。
                        int dir, ph;
                        K pk = p.key;
                        if ((ph = p.hash) > h)
                            dir = -1;
                        else if (ph < h)
                            dir = 1;
                        //如果hash值相等，那么判断k是否实现了comparable接口，如果实现了comparable接口就使用compareTo进行进行比较，如果仍旧相等或者没有实现comparable接口，则在tieBreakOrder中比较
                        else if ((kc == null &&
                                  (kc = comparableClassFor(k)) == null) ||
                                 (dir = compareComparables(kc, k, pk)) == 0)
                            dir = tieBreakOrder(k, pk);

                        TreeNode<K,V> xp = p;
                        if ((p = (dir <= 0) ? p.left : p.right) == null) {
                            x.parent = xp;
                            if (dir <= 0)
                                xp.left = x;
                            else
                                xp.right = x;　　　　　　　　　　　　　　　　 //进行插入平衡处理
                            root = balanceInsertion(root, x);
                            break;
                        }
                    }
                }
            }　　　　　　　//确保给定节点是桶中的第一个元素
            moveRootToFront(tab, root);
        }    
     //这里不是为了整体排序，而是为了在插入中保持一致的顺序
     static int tieBreakOrder(Object a, Object b) {
            int d;
            //用两者的类名进行比较，如果相同则使用对象默认的hashcode进行比较
            if (a == null || b == null ||
                (d = a.getClass().getName().
                 compareTo(b.getClass().getName())) == 0)
                d = (System.identityHashCode(a) <= System.identityHashCode(b) ?
                     -1 : 1);
            return d;
        }

这里的逻辑其实不复杂，仅仅是循环遍历当前树，然后找到可以该节点可以插入的位置，依次和遍历节点比较，比它大则跟其右孩子比较，小则与其左孩子比较，依次遍历，直到找到左孩子或者右孩子为null的位置进行插入。

真正复杂一点的地方在于balanceInsertion函数，这个函数中，将红黑树进行插入平衡处理，保证插入节点后仍保持红黑树的性质。这个函数稍后在TreeNode的插入中进行介绍，这里先看看moveRootToFront，这个函数是将root节点移动到桶中的第一个元素，也就是链表的首节点，这样做是因为在判断桶中元素类型的时候会对链表进行遍历，将根节点移动到链表前端可以确保类型判断时不会出现错误。

/**
 * 把给定节点设为桶中的第一个元素
 */        
    static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
            int n;
            if (root != null && tab != null && (n = tab.length) > 0) {
                int index = (n - 1) & root.hash;
                //first指向链表第一个节点
                TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
                if (root != first) {
                    //如果root不是第一个节点，则将root放到第一个首节点位置
                    Node<K,V> rn;
                    tab[index] = root;
                    TreeNode<K,V> rp = root.prev;
                    if ((rn = root.next) != null)
                        ((TreeNode<K,V>)rn).prev = rp;
                    if (rp != null)
                        rp.next = rn;
                    if (first != null)
                        first.prev = root;
                    root.next = first;
                    root.prev = null;
                }
                //这里是防御性编程，校验更改后的结构是否满足红黑树和双链表的特性
                //因为HashMap并没有做并发安全处理，可能在并发场景中意外破坏了结构
                assert checkInvariants(root);
            }
        }

红黑树的左旋和右旋

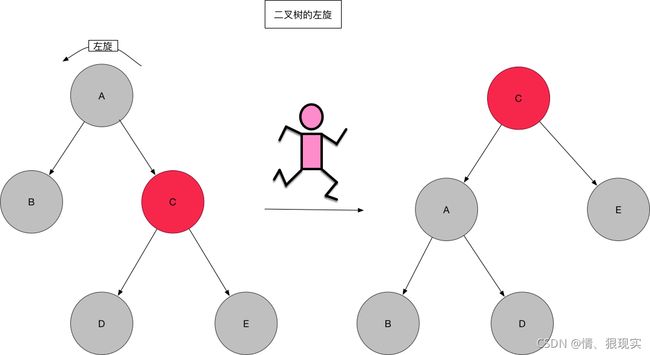
左旋和右旋，顾名思义嘛，就是将节点以某个节点为中心向左或者向右进行旋转操作以保持二叉树的平衡，让我们看图说话

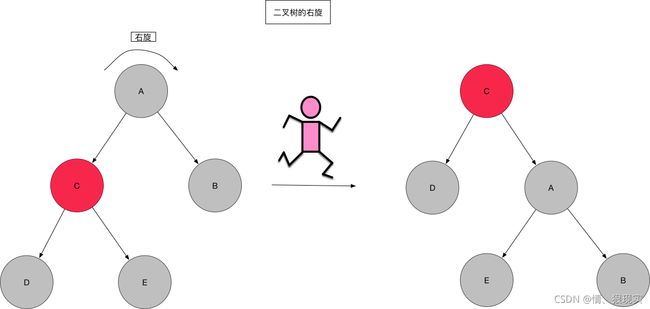
图画的有点大。将就着看一下吧，左旋相当于以要旋转的节点为中心，将子树整体向左旋转，该节点变成子树的根节点，原来的父节点A变成了左孩子，如果右孩子C有左孩子D，则将其变为A的右孩子。说起来好像有点绕，可以联系图进行形象化的理解，当节点A向左旋转之后，C的左孩子D可以理解为因为重力作用掉到A的右孩子位置，嗯，就是这样。右旋也是类似理解即可。

TreeNode的左旋和右旋

了解了左旋和右旋，让我们看看代码里是怎样实现的：

        /**
         * 左旋
         */
        static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
                                              TreeNode<K,V> p) {
            //这里的p即上图的A节点，r指向右孩子即C，rl指向右孩子的左孩子即D，pp为p的父节点
            TreeNode<K,V> r, pp, rl;
            if (p != null && (r = p.right) != null) {
                if ((rl = p.right = r.left) != null)
                    rl.parent = p;
                //将p的父节点的孩子节点指向r
                if ((pp = r.parent = p.parent) == null)
                    (root = r).red = false;
                else if (pp.left == p)
                    pp.left = r;
                else
                    pp.right = r;
                //将p置为r的左节点
                r.left = p;
                p.parent = r;
            }
            return root;
        }

        /**
         * 右旋
         */
        static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
                                               TreeNode<K,V> p) {
             //这里的p即上图的A节点，l指向左孩子即C，lr指向左孩子的右孩子即E，pp为p的父节点
            TreeNode<K,V> l, pp, lr;
            if (p != null && (l = p.left) != null) {
                if ((lr = p.left = l.right) != null)
                    lr.parent = p;
                if ((pp = l.parent = p.parent) == null)
                    (root = l).red = false;
                else if (pp.right == p)
                    pp.right = l;
                else
                    pp.left = l;
                l.right = p;
                p.parent = l;
            }
            return root;
        }

红黑树的插入

现在来看看一个比较麻烦一点的操作，红黑树的插入，首先找到这个节点要插入的位置，即一层一层比较，大的放右边，小的放左边，直到找到为null的节点放入即可，但是如何在插入的过程保持红黑树的特性呢，想想好像比较头疼，但是再仔细想想其实就会发现，其实只有这么几种情况：

1.插入的为根节点，则直接把颜色改成黑色即可。

2.插入的节点的父节点是黑色节点，则不需要调整，因为插入的节点会初始化为红色节点，红色节点是不会影响树的平衡的。

3.插入的节点的祖父节点为null，即插入的节点的父节点是根节点，直接插入即可（因为根节点肯定是黑色）。

4.插入的节点父节点和祖父节点都存在，并且其父节点是祖父节点的左节点。这种情况稍微麻烦一点，又分两种子情况：

i.插入节点的叔叔节点是红色，则将父亲节点和叔叔节点都改成黑色，然后祖父节点改成红色即可。

ii.插入节点的叔叔节点是黑色或不存在：

a.若插入节点是其父节点的右孩子，则将其父节点左旋，

b.若为左孩子，则将其父节点变成黑色节点，将其祖父节点变成红色节点，然后将其祖父节点右旋。

5.插入的节点父节点和祖父节点都存在，并且其父节点是祖父节点的右节点。这种情况跟上面是类似的，分两种子情况：

i.插入节点的叔叔节点是红色，则将父亲节点和叔叔节点都改成黑色，然后祖父节点改成红色即可。

ii.插入节点的叔叔节点是黑色或不存在：

a.若插入节点是其父节点的左孩子，则将其父节点右旋

b.若为右孩子，则将其父节点变成黑色节点，将其祖父节点变成红色节点，然后将其祖父节点左旋。

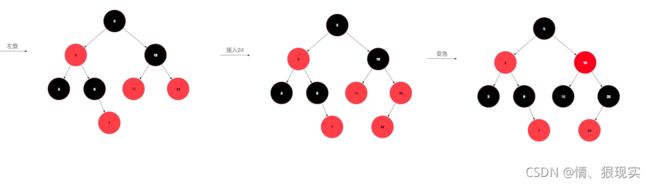
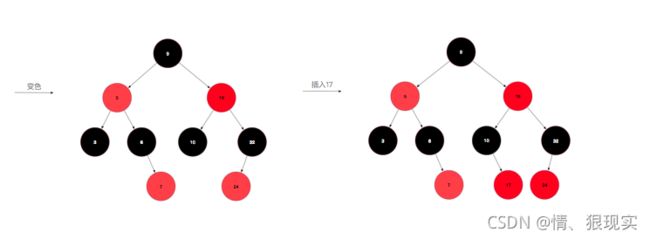
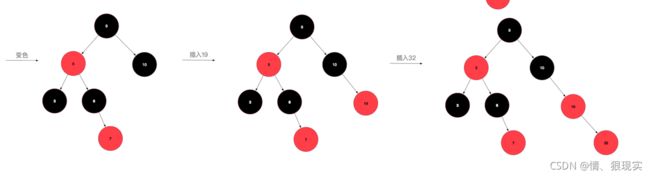
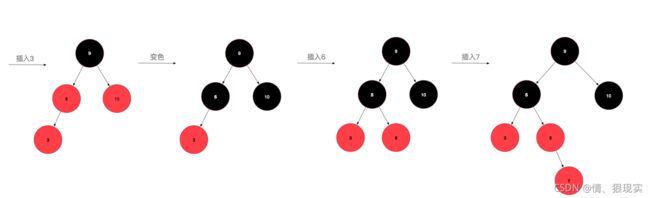
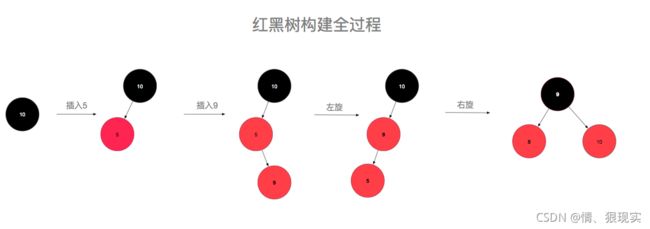
然后重复进行上述操作，直到变成1或2情况时则结束变换。说半天，可能还是云里雾里，一图胜千言，让我们从无到有构建一颗红黑树，假设插入的顺序为：10，5，9，3，6，7，19，32，24，17（数字是我拍脑袋瞎想的。）

先来插个10，为情景1，直接改成黑色即可，再插入5，为情景2，比10小，放到10的左孩子位置，插入9，比10小，但是比5大，放到5的右孩子位置，此时，为情景4iia，左旋后变成了情景4iib，变色右旋即可完成转化。插入3后为情景4i，将父节点和叔叔节点同时变色即可，插入6不需要调整，插入7后为情景5i，变色即可。插入19不需要调整，插入32，变成了5iib，左旋变色即可，插入24，变成5iia，右旋后变成5i，变色即可，最后插入17，完美。

TreeNode的插入

了解了红黑树的删除之后，我们再来看下TreeNode中是怎样用代码实现的：

      static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
                                                    TreeNode<K,V> x) {
            x.red = true;
            for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {                //情景1：父节点为null
                if ((xp = x.parent) == null) {
                    x.red = false;
                    return x;
                }　　　　　　　　　 //情景2，3：父节点是黑色节点或者祖父节点为null
                else if (!xp.red || (xpp = xp.parent) == null)
                    return root;　　　　　　　　　　//情景4：插入的节点父节点和祖父节点都存在，并且其父节点是祖父节点的左节点
                if (xp == (xppl = xpp.left)) {　　　　　　　　　　　　//情景4i：插入节点的叔叔节点是红色
                    if ((xppr = xpp.right) != null && xppr.red) {
                        xppr.red = false;
                        xp.red = false;
                        xpp.red = true;
                        x = xpp;
                    }　　　　　　　　　　　　//情景4ii：插入节点的叔叔节点是黑色或不存在
                    else {　　　　　　　　　　　　　　//情景4iia：插入节点是其父节点的右孩子
                        if (x == xp.right) {
                            root = rotateLeft(root, x = xp);
                            xpp = (xp = x.parent) == null ? null : xp.parent;
                        }　　　　　　　　　　　　　　//情景4iib：插入节点是其父节点的左孩子
                        if (xp != null) {
                            xp.red = false;
                            if (xpp != null) {
                                xpp.red = true;
                                root = rotateRight(root, xpp);
                            }
                        }
                    }
                }　　　　　　　　　 //情景5：插入的节点父节点和祖父节点都存在，并且其父节点是祖父节点的右节点
                else {　　　　　　　　　　　　//情景5i：插入节点的叔叔节点是红色
                    if (xppl != null && xppl.red) {
                        xppl.red = false;
                        xp.red = false;
                        xpp.red = true;
                        x = xpp;
                    }　　　　　　　　　　　　//情景5ii：插入节点的叔叔节点是黑色或不存在
                    else {·　　　　　　　　　　　　　　//情景5iia：插入节点是其父节点的左孩子　
                        if (x == xp.left) {
                            root = rotateRight(root, x = xp);
                            xpp = (xp = x.parent) == null ? null : xp.parent;
                        }　　　　　　　　　　　　　　//情景5iib：插入节点是其父节点的右孩子
                        if (xp != null) {
                            xp.red = false;
                            if (xpp != null) {
                                xpp.red = true;
                                root = rotateLeft(root, xpp);
                            }
                        }
                    }
                }
            }
        }

其实就是一毛一样的，对号入座即可。

红黑树的删除

讲完插入，接下来我们来说说删除，删除的话，比插入还要复杂一点，请各位看官先深呼吸，做好阅读准备。

之前已经说过，红黑树是一颗特殊的二叉搜索树，所以进行删除操作时，其实是先进行二叉搜索树的删除，然后再进行调整。所以，其实这里分为两部分内容：1.二叉搜索树的删除，2.红黑树的删除调整。

二叉搜索树的删除主要有这么几种情景：

情景1：待删除的节点无左右孩子。

情景2：待删除的节点只有左孩子或者右孩子。

情景3：待删除的节点既有左孩子又有右孩子。

对于情景1，直接删除即可，情景2，则直接把该节点的父节点指向它的左孩子或者右孩子即可，情景3稍微复杂一点，需要先找到其右子树的最左孩子（或者左子树的最右孩子），即左（右）子树中序遍历时的第一个节点，然后将其与待删除的节点互换，最后再删除该节点（如果有右子树，则右子树上位）。总之，就是先找到它的替代者，找到之后替换这个要删除的节点，然后再把这个节点真正删除掉。

其实二叉搜索树的删除总体来说还是比较简单的，删除完之后，如果替代者是红色节点，则不需要调整，如果是黑色节点，则会导致左子树和右子树路径中黑色节点数量不一致，需要进行红黑树的调整，跟上面一样，替代节点为其父节点的左孩子与右孩子的情况类似，所以这里只说其为左孩子的情景（PS:上一步的寻找替换节点使用的是右子树的最左节点，所以该节点如果有孩子，只能是右孩子）：

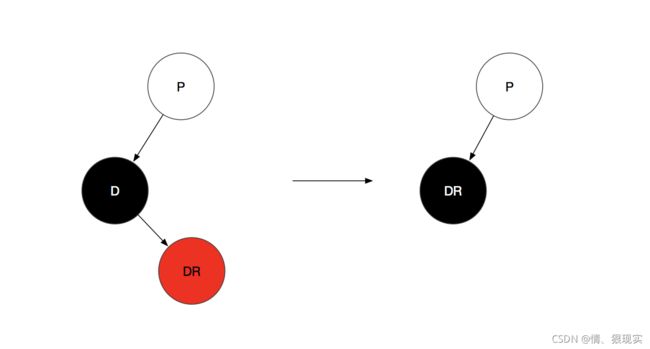
情景1：只有右孩子且为红色，直接用右孩子替换该节点然后变成黑色即可。

（D代表替代节点，即要被删除的节点，之前在经过二叉搜索树的删除后，D节点其实已经被删除了，这里为了方便理解这个变化过程，所以把这个节点也画出来了，所以当前的初始状态是待删除节点与其替换节点互换位置与颜色之后的状态）

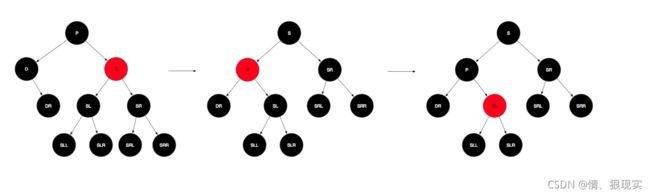
情景2：只有右孩子且为黑色，那么删除该节点会导致父节点的左子树路径上黑色节点减一，此时只能去借助右子树，从右子树中借一个红色节点过来即可，具体取决于右子树的情况，这里又分成两种：

i.兄弟节点是红色，则此时父节点是黑色，且兄弟节点肯定有两个孩子，且兄弟节点的左右子树路径上均有两个黑色节点，此时只需将兄弟节点与父节点颜色互换，然后将父节点左旋，左旋后，兄弟节点的左子树SL挂到了父节点p的右孩子位置，这时会导致p的右子树路径上的黑色节点比左子树多一，此时再SL置为红色即可。

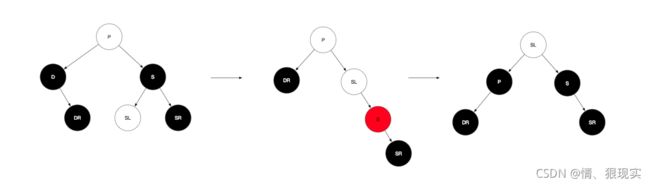
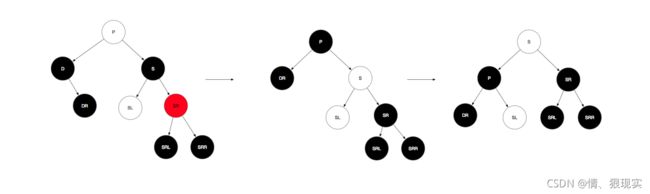
ii.兄弟节点是黑色，那么就只能打它孩子的主意了，这里主要关注远侄子（兄弟节点的右孩子，即SR）的颜色情况，这里分成两种情况：

a.远侄子SR是黑色，近侄子任意（白色代表颜色可为任意颜色），则先将S转为红色，然后右旋，再将SL换成P节点颜色，P涂成黑色，S也涂成黑色，再进行左旋即可。其实简单说就是SL上位，替换父节点位置。

b.远侄子SR为红色，近侄子任意（该子树路径中有且仅有一个黑色节点），则先将兄弟节点与父节点颜色互换，将SR涂成黑色，再将父节点左旋即可。

TreeNode的删除节点

TreeNode删除节点其实也是两步走，先进行二叉搜索树的删除，然后再进行红黑树的调整，跟之前的情况分析是一致的。

final void removeTreeNode(HashMap map, Node[] tab, boolean movable) {

     ......

     //p是待删除节点，replacement用于后续的红黑树调整，指向的是p或者p的继承者。
     //如果p是叶子节点，p==replacement，否则replacement为p的右子树中最左节点
     if (replacement != p) {
        //若p不是叶子节点，则让replacement的父节点指向p的父节点
        TreeNode pp = replacement.parent = p.parent;
        if (pp == null)
            root = replacement;
        else if (p == pp.left)
            pp.left = replacement;
        else
            pp.right = replacement;
        p.left = p.right = p.parent = null;
    }

    //若待删除的节点p时红色的，则树平衡未被破坏，无需进行调整。
    //否则删除节点后需要进行调整
    TreeNode r = p.red ? root : balanceDeletion(root, replacement);

    //p为叶子节点，则直接将p从树中清除
    if (replacement == p) {  // detach
        TreeNode pp = p.parent;
        p.parent = null;
        if (pp != null) {
            if (p == pp.left)
                pp.left = null;
            else if (p == pp.right)
                pp.right = null;
        }
    }
}

麻烦的地方就在删除节点后的调整了，所有逻辑都在balanceDeletion函数里，两个参数分别表示根节点和删除节点的继承者，来看看它的具体实现：

static  TreeNode balanceDeletion(TreeNode root, TreeNode x) {
    for (TreeNode xp, xpl, xpr;;)  {
        //x为空或x为根节点，直接返回
        if (x == null || x == root)
            return root; 
        //x为根节点，染成黑色，直接返回（因为调整过后，root并不一定指向删除操作过后的根节点，如果之前删除的是root节点，则x将成为新的根节点）
        else if ((xp = x.parent) == null) {
            x.red = false; 
            return x;
        }
        //如果x为红色，则无需调整，返回
        else if (x.red) {
            x.red = false;
            return root; 
        }
        //x为其父节点的左孩子
        else if ((xpl = xp.left) == x) {
            //如果它有红色的兄弟节点xpr，那么它的父亲节点xp一定是黑色节点
            if ((xpr = xp.right) != null && xpr.red) { 
                xpr.red = false;
                xp.red = true; 
                //对父节点xp做左旋转
                root = rotateLeft(root, xp); 
                //重新将xp指向x的父节点，xpr指向xp新的右孩子
                xpr = (xp = x.parent) == null ? null : xp.right; 
            }
            //如果xpr为空，则向上继续调整，将x的父节点xp作为新的x继续循环
            if (xpr == null)
                x = xp; 
            else {
                //sl和sr分别为其近侄子和远侄子
                TreeNode sl = xpr.left, sr = xpr.right;　　　　　　　　　　　　
                if ((sr == null || !sr.red) &&
                    (sl == null || !sl.red)) {
                    xpr.red = true; //若sl和sr都为黑色或者不存在，即xpr没有红色孩子，则将xpr染红
                    x = xp; //本轮结束，继续向上循环
                }
                else {
                    //否则的话，就需要进一步调整
                    if (sr == null || !sr.red) { 
                        if (sl != null) //若左孩子为红，右孩子不存在或为黑
                            sl.red = false; //左孩子染黑
                        xpr.red = true; //将xpr染红
                        root = rotateRight(root, xpr); //右旋
                        xpr = (xp = x.parent) == null ?
                            null : xp.right;  //右旋后，xpr指向xp的新右孩子，即上一步中的sl
                    }
                    if (xpr != null) {
                        xpr.red = (xp == null) ? false : xp.red; //xpr染成跟父节点一致的颜色，为后面父节点xp的左旋做准备
                        if ((sr = xpr.right) != null)
                            sr.red = false; //xpr新的右孩子染黑，防止出现两个红色相连
                    }
                    if (xp != null) {
                        xp.red = false; //将xp染黑，并对其左旋，这样就能保证被删除的X所在的路径又多了一个黑色节点，从而达到恢复平衡的目的
                        root = rotateLeft(root, xp);
                    }
                    //到此调整已经完毕，进入下一次循环后将直接退出
                    x = root;
                }
            }
        }
        //x为其父节点的右孩子，跟上面类似
        else { // symmetric
            if (xpl != null && xpl.red) {
                xpl.red = false;
                xp.red = true;
                root = rotateRight(root, xp);
                xpl = (xp = x.parent) == null ? null : xp.left;
            }
            if (xpl == null)
                x = xp;
            else {
                TreeNode sl = xpl.left, sr = xpl.right;
                if ((sl == null || !sl.red) &&
                    (sr == null || !sr.red)) {
                    xpl.red = true;
                    x = xp;

基础部分源码

public class HashMap<K, V> extends AbstractMap<K, V>
        implements Map<K, V>, Cloneable, Serializable {

    private static final long serialVersionUID = 362498820763181265L;

    /*
     * Implementation notes.
     *
     * 实现注意事项。
     *
     * This map usually acts as a binned (bucketed) hash table, but
     * when bins get too large, they are transformed into bins of
     * TreeNodes, each structured similarly to those in
     * java.util.TreeMap. Most methods try to use normal bins, but
     * relay to TreeNode methods when applicable (simply by checking
     * instanceof a node).  Bins of TreeNodes may be traversed and
     * used like any others, but additionally support faster lookup
     * when overpopulated. However, since the vast majority of bins in
     * normal use are not overpopulated, checking for existence of
     * tree bins may be delayed in the course of table methods.
     *
     * 这个映射通常充当一个装了好多桶的哈希表，但是当桶变得太大时，它们会被转换成树节点的桶
     * ，每个桶的结构都类似于java.util.TreeMap中的桶。
     * 大多数方法都尝试使用普通的桶（链表形式），但在适用时中继到TreeNode方法(只需检查节点的instanceof)。
     * 树节点的存储箱可以像其他存储箱一样被遍历和使用，但是在过度填充时支持更快的查找。
     * 但是，由于正常使用的大多数桶并没有过度填充，所以在表方法的过程中可能会延迟检查树桶是否存在。
     *
     * Tree bins (i.e., bins whose elements are all TreeNodes) are
     * ordered primarily by hashCode, but in the case of ties, if two
     * elements are of the same "class C implements Comparable",
     * type then their compareTo method is used for ordering. (We
     * conservatively check generic types via reflection to validate
     * this -- see method comparableClassFor).  The added complexity
     * of tree bins is worthwhile in providing worst-case O(log n)
     * operations when keys either have distinct hashes or are
     * orderable, Thus, performance degrades gracefully under
     * accidental or malicious usages in which hashCode() methods
     * return values that are poorly distributed, as well as those in
     * which many keys share a hashCode, so long as they are also
     * Comparable. (If neither of these apply, we may waste about a
     * factor of two in time and space compared to taking no
     * precautions. But the only known cases stem from poor user
     * programming practices that are already so slow that this makes
     * little difference.)
     *
     * 树形桶(即其元素都是TreeNode的桶)主要由hashCode排序，
     * 但在链接的情况下，如果两个元素属于相同的“class C implementation Comparable”，
     * 则键入它们的compareTo方法来排序。
     * (我们通过反射保守地检查泛型类型来验证这一点——请参见comparableClassFor方法)。
     * 当键具有不同的哈希值或可排序时，在提供最坏情况O(log n)操作时，树箱增加的复杂性是值得的。
     * 因此，在hashCode()方法返回分布很差的值的意外或恶意使用中，
     * 以及在许多键共享一个hashCode的情况下(只要它们也是可比较的)，性能会优雅地下降。
     * (如果这两种方法都不适用，与不采取预防措施相比，我们可能会浪费大约两倍的时间和空间。
     * 但目前所知的唯一案例来自于糟糕的用户编程实践，这些实践已经非常缓慢，以至于没有什么区别。)
     *
     * Because TreeNodes are about twice the size of regular nodes, we
     * use them only when bins contain enough nodes to warrant use
     * (see TREEIFY_THRESHOLD). And when they become too small (due to
     * removal or resizing) they are converted back to plain bins.  In
     * usages with well-distributed user hashCodes, tree bins are
     * rarely used.  Ideally, under random hashCodes, the frequency of
     * nodes in bins follows a Poisson distribution
     * (http://en.wikipedia.org/wiki/Poisson_distribution) with a
     * parameter of about 0.5 on average for the default resizing
     * threshold of 0.75, although with a large variance because of
     * resizing granularity. Ignoring variance, the expected
     * occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
     * factorial(k)). The first values are:
     *
     * 因为树节点的大小大约是普通节点的两倍，所以我们只在桶中包含足够的节点以保证使用时才使用它们(请参阅TREEIFY_THRESHOLD)。
     * 当它们变得太小(由于移除或调整大小)，就会被转换回普通的桶。
     * 在使用分布良好的用户哈希码时，很少使用树箱。
     * 理想情况下，在随机哈希码下，bin中节点的频率遵循泊松分布(http://en.wikipedia.org/wiki/Poisson_distribution)，
     * 默认调整阈值为0.75，平均参数约为0.5，尽管由于调整粒度而存在较大的差异。
     * 忽略方差，列表大小k的预期出现次数为(exp(-0.5) pow(0.5, k) / factorial(k))
     * 第一个值是：
     *
     * 0:    0.60653066
     * 1:    0.30326533
     * 2:    0.07581633
     * 3:    0.01263606
     * 4:    0.00157952
     * 5:    0.00015795
     * 6:    0.00001316
     * 7:    0.00000094
     * 8:    0.00000006
     * more: less than 1 in ten million
     * more: 少于千万分之一
     *
     * The root of a tree bin is normally its first node.  However,
     * sometimes (currently only upon Iterator.remove), the root might
     * be elsewhere, but can be recovered following parent links
     * (method TreeNode.root()).
     *
     * 树状容器的根通常是它的第一个节点。
     * 但是，有时(目前仅在Iterator.remove之后)，根可能在其他地方，
     * 但是可以通过父链接(方法TreeNode.root())恢复。
     *
     * All applicable internal methods accept a hash code as an
     * argument (as normally supplied from a public method), allowing
     * them to call each other without recomputing user hashCodes.
     * Most internal methods also accept a "tab" argument, that is
     * normally the current table, but may be a new or old one when
     * resizing or converting.
     *
     * 所有适用的内部方法都接受散列代码作为参数(通常由公共方法提供)，允许它们在不重新计算用户散列代码的情况下相互调用。
     * 大多数内部方法也接受“tab”参数，这通常是当前表，但在调整大小或转换时可能是新的或旧的。
     *
     * When bin lists are treeified, split, or untreeified, we keep
     * them in the same relative access/traversal order (i.e., field
     * Node.next) to better preserve locality, and to slightly
     * simplify handling of splits and traversals that invoke
     * iterator.remove. When using comparators on insertion, to keep a
     * total ordering (or as close as is required here) across
     * rebalancings, we compare classes and identityHashCodes as
     * tie-breakers.
     *
     * 当bin列表被treeified、split或untreeified时，我们将它们保持相同的相对访问/遍历顺序(即为了更好地保存局部，
     * 并稍微简化对调用iterator.remove的分割和遍历的处理。
     * 当在插入时使用比较器时，为了保持整个重新平衡的顺序(或尽可能接近这里的要求)
     * ，我们将类和dentityhashcode作为连接符进行比较。
     *
     * The use and transitions among plain vs tree modes is
     * complicated by the existence of subclass LinkedHashMap. See
     * below for hook methods defined to be invoked upon insertion,
     * removal and access that allow LinkedHashMap internals to
     * otherwise remain independent of these mechanics. (This also
     * requires that a map instance be passed to some utility methods
     * that may create new nodes.)
     *
     * 由于LinkedHashMap子类的存在，普通vs树模式之间的使用和转换变得复杂。
     * 有关定义在插入、删除和访问时调用的钩子方法，请参见下面，这些方法允许LinkedHashMap内部保持独立于这些机制。
     * (这还要求将map实例传递给一些可能创建新节点的实用方法。)
     *
     * The concurrent-programming-like SSA-based coding style helps
     * avoid aliasing errors amid all of the twisty pointer operations.
     *
     * 基于并行编程的类似于ssa的编码风格有助于避免所有扭曲指针操作中的混叠错误。
     */

    /**
     * The default initial capacity - MUST be a power of two.
     * 默认初始容量—必须是2的幂。
     * 为啥不直接写16？？
     */
    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16：

    /**
     * The maximum capacity, used if a higher value is implicitly specified
     * by either of the constructors with arguments.
     * MUST be a power of two <= 1<<30.
     * 最大容量，如果较高的值由带参数的任何构造函数隐式指定，则使用该值。必须是2的幂 <= 1<<30。
     */
    static final int MAXIMUM_CAPACITY = 1 << 30;

    /**
     * The load factor used when none specified in constructor.
     * 构造函数中没有指定时使用的负载因子。
     */
    static final float DEFAULT_LOAD_FACTOR = 0.75f;

    /**
     * The bin count threshold for using a tree rather than list for a
     * bin.  Bins are converted to trees when adding an element to a
     * bin with at least this many nodes. The value must be greater
     * than 2 and should be at least 8 to mesh with assumptions in
     * tree removal about conversion back to plain bins upon
     * shrinkage.
     * 使用树(而不是列表)来设置桶的计数阈值。当向至少具有这么多节点的桶添加元素时，桶将转换为树。
     * 该值必须大于2，并且应该至少为8，以便与树木移除中关于收缩后转换回普通桶的假设相吻合。
     * 为啥不是 1 << 3 ?
     */
    static final int TREEIFY_THRESHOLD = 8;

    /**
     * The bin count threshold for untreeifying a (split) bin during a
     * resize operation. Should be less than TREEIFY_THRESHOLD, and at
     * most 6 to mesh with shrinkage detection under removal.
     * 用于在调整大小操作期间反树化(拆分)桶的计数阈值。
     * 应小于TREEIFY_THRESHOLD，且最多6个以配合收缩检测下删除。
     */
    static final int UNTREEIFY_THRESHOLD = 6;

    /**
     * The smallest table capacity for which bins may be treeified.
     * (Otherwise the table is resized if too many nodes in a bin.)
     * Should be at least 4 * TREEIFY_THRESHOLD to avoid conflicts
     * between resizing and treeification thresholds.
     * 最小的表容量，其中的桶可以树化。(否则，如果一个桶中有太多节点，则会调整表的大小。)
     * 应至少为4 * TREEIFY_THRESHOLD，以避免调整大小和treeification阈值之间的冲突。
     */
    static final int MIN_TREEIFY_CAPACITY = 64;

    /**
     * Basic hash bin node, used for most entries.  (See below for
     * TreeNode subclass, and in LinkedHashMap for its Entry subclass.)
     * 基本哈希桶节点，用于大多数条目。(参见下面的TreeNode子类和LinkedHashMap中的Entry子类。)
     */
    static class Node<K, V> implements Entry<K, V> {
        // 哈希值
        final int hash;
        // 键
        final K key;
        // 值
        V value;
        // 写一个Node节点的引用
        Node<K, V> next;

        Node(int hash, K key, V value, Node<K, V> next) {
            this.hash = hash;
            this.key = key;
            this.value = value;
            this.next = next;
        }

        public final K getKey() {
            return key;
        }

        public final V getValue() {
            return value;
        }

        public final String toString() {
            return key + "=" + value;
        }

        public final int hashCode() {
            // 位异或运算（^）：两个数转为二进制，然后从高位开始比较，如果相同则为0，不相同则为1
            return Objects.hashCode(key) ^ Objects.hashCode(value);
        }

        public final V setValue(V newValue) {
            V oldValue = value;
            value = newValue;
            return oldValue;
        }

        public final boolean equals(Object o) {
            if (o == this)
                return true;
            if (o instanceof Map.Entry) {
                Entry<?, ?> e = (Entry<?, ?>) o;
                if (Objects.equals(key, e.getKey()) &&
                        Objects.equals(value, e.getValue()))
                    return true;
            }
            return false;
        }
    }

    /* ---------------- Static utilities -------------- */
    /* ---------------- 静态工具 -------------- */
    /**
     * Computes key.hashCode() and spreads (XORs) higher bits of hash
     * to lower.  Because the table uses power-of-two masking, sets of
     * hashes that vary only in bits above the current mask will
     * always collide. (Among known examples are sets of Float keys
     * holding consecutive whole numbers in small tables.)  So we
     * apply a transform that spreads the impact of higher bits
     * downward. There is a tradeoff between speed, utility, and
     * quality of bit-spreading. Because many common sets of hashes
     * are already reasonably distributed (so don't benefit from
     * spreading), and because we use trees to handle large sets of
     * collisions in bins, we just XOR some shifted bits in the
     * cheapest possible way to reduce systematic lossage, as well as
     * to incorporate impact of the highest bits that would otherwise
     * never be used in index calculations because of table bounds.
     * 由于该表使用了2的幂掩码，因此仅在当前掩码之上以位为单位变化的散列集总是会发生冲突。
     * (已知的例子包括在小表中保存连续整数的浮点键集。)因此，我们应用一个转换，将更高位的影响向下传播。
     * 位扩展的速度、实用性和质量之间存在权衡。
     * 
     * 因为许多常见的散列集已经合理分布(所以不要受益于传播),
     * 在桶中我们用树来处理大型的碰撞,通过异或一些位的改变以最优的的方式来减少系统lossage,纳入最高位的影响,
     * 否则，由于表范围，将永远不会在索引计算中使用它。
     * 

     * 计算key的hashCode值h
     * h无符号右移16位，得到h的高16位
     * h与其高16位异或。
     */
    static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }

    /**
     * Returns x's Class if it is of the form "class C implements
     * Comparable", else null.
     * 如果x实现了Comparable接口，则返回x的类，否则返回null
     */
    static Class<?> comparableClassFor(Object x) {
        if (x instanceof Comparable) {
            Class<?> c;
            Type[] ts, as;
            Type t;
            ParameterizedType p;
            //如果是String类型，直接返回String.class
            if ((c = x.getClass()) == String.class) // bypass checks
                return c;
            //获取所有的实现接口，迭代
            if ((ts = c.getGenericInterfaces()) != null) {
                for (int i = 0; i < ts.length; ++i) {
                    //如果为参数化类型，且为Comparable
                    if (((t = ts[i]) instanceof ParameterizedType) &&
                            ((p = (ParameterizedType) t).getRawType() ==
                                    Comparable.class) &&
                            (as = p.getActualTypeArguments()) != null &&
                            as.length == 1 && as[0] == c) // type arg is c
                        return c;
                }
            }
        }
        return null;
    }

    /**
     * Returns k.compareTo(x) if x matches kc (k's screened comparable
     * class), else 0.
     * 比较k与x
     */
    @SuppressWarnings({"rawtypes", "unchecked"}) // for cast to Comparable
    static int compareComparables(Class<?> kc, Object k, Object x) {
        return (x == null || x.getClass() != kc ? 0 :
                ((Comparable) k).compareTo(x));
    }

    /**
     * Returns a power of two size for the given target capacity.
     * 返回给定目标容量的2次幂。
     * 无符号右移  ， 按位或，很高明的做法
     * 假设cap=8
     * 第一行：n=7     二进制： 0000 0000 0000 0000 0000 0000 0000 0111
     * 第二行：n无符号右移1位： 0000 0000 0000 0000 0000 0000 0000 0011
     * 与上一步n或：  0000 0000 0000 0000 0000 0000 0000 0111
     * n=7     二进制： 0000 0000 0000 0000 0000 0000 0000 0111
     * 第三行：n无符号右移2位： 0000 0000 0000 0000 0000 0000 0000 0001
     * 与上一步n或： 0000 0000 0000 0000 0000 0000 0000 0111
     * n=7     二进制： 0000 0000 0000 0000 0000 0000 0000 0111
     * 第四行：n无符号右移4位： 0000 0000 0000 0000 0000 0000 0000 0000
     * 与上一步n或： 0000 0000 0000 0000 0000 0000 0000 0111
     * n=7     二进制： 0000 0000 0000 0000 0000 0000 0000 0111
     * 第五行：n无符号右移8位： 0000 0000 0000 0000 0000 0000 0000 0000
     * 与上一步n或： 0000 0000 0000 0000 0000 0000 0000 0111
     * n=7     二进制： 0000 0000 0000 0000 0000 0000 0000 0111
     * 第五行：n无符号右移16位： 0000 0000 0000 0000 0000 0000 0000 0000
     * 与上一步n或： 0000 0000 0000 0000 0000 0000 0000 0111
     * n=7     二进制： 0000 0000 0000 0000 0000 0000 0000 0101
     * 第六行：n不小于0，也不大于等于1<<30 ,所以 n=n+1=8
     * 

     * 假设           cap=0100 0000 0000 0000 0000 0000 0000 0000   1个1
     * 1:   无符号右移1位：0010 0000 0000 0000 0000 0000 0000 0000
     * 或操作：0110 0000 0000 0000 0000 0000 0000 0000   2个1
     * 2:   无符号右移2位：0001 1000 0000 0000 0000 0000 0000 0000
     * 或操作：0111 1000 0000 0000 0000 0000 0000 0000   4个1
     * 3:   无符号右移4位：0000 0111 1000 0000 0000 0000 0000 0000
     * 或操作：0111 1111 1000 0000 0000 0000 0000 0000   8个1
     * 4:   无符号右移8位：0000 0000 0111 1111 1000 0000 0000 0000
     * 或操作：0111 1111 1111 1111 1000 0000 0000 0000   16个1
     * 4:  无符号右移16位：0000 0000 0000 0000 0111 1111 1111 1111
     * 或操作：0111 1111 1111 1111 1111 1111 1111 1111   31个1
     * 5：        结果+1：1000 0000 0000 0000 0000 0000 0000 0000   即2^30;1 << 30。最大值
     * 

     * 发现一个规律：无符号右移再位或的最终结果会将二进制首个1的后面所有位都变成1，最后结果再加1，则向前进位（前提不溢出），
     * 结果必是2的幂
     */
    static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

    /* ---------------- Fields -------------- */

    /**
     * The table, initialized on first use, and resized as
     * necessary. When allocated, length is always a power of two.
     * (We also tolerate length zero in some operations to allow
     * bootstrapping mechanics that are currently not needed.)
     * 表，第一次使用时初始化，并根据需要调整大小。当分配时，长度总是2的幂。
     * (在某些操作中，我们还允许长度为零，以允许当前不需要的引导机制。)
     */
    transient Node<K, V>[] table;

    /**
     * Holds cached entrySet(). Note that AbstractMap fields are used
     * for keySet() and values().
     * 保存缓存entrySet ()。AbstractMap字段用于keySet()和values()。
     */
    transient Set<Entry<K, V>> entrySet;

    /**
     * The number of key-value mappings contained in this map.
     * 此映射中包含的键值映射的数目。
     */
    transient int size;

    /**
     * The number of times this HashMap has been structurally modified
     * Structural modifications are those that change the number of mappings in
     * the HashMap or otherwise modify its internal structure (e.g.,
     * rehash).  This field is used to make iterators on Collection-views of
     * the HashMap fail-fast.  (See ConcurrentModificationException).
     * 

     * 这个HashMap在结构上被修改的次数，结构修改是指改变HashMap中映射的数量或修改其内部结构的次数(例如，rehash)。
     * 此字段用于使HashMap集合视图上的迭代器快速失效。(见ConcurrentModificationException)。
     */
    transient int modCount;

    /**
     * The next size value at which to resize (capacity * load factor).
     * 要调整大小的下一个大小阈值=(capacity * load factor)
     *
     * @serial
     */
    // (The javadoc description is true upon serialization.
    // Additionally, if the table array has not been allocated, this
    // field holds the initial array capacity, or zero signifying
    // DEFAULT_INITIAL_CAPACITY.)
    int threshold;

    /**
     * The load factor for the hash table.
     * 哈希表的加载因子
     *
     * @serial
     */
    final float loadFactor;

    /* ---------------- Public operations -------------- */

    /**
     * Constructs an empty HashMap with the specified initial
     * capacity and load factor.
     * 构造一个具有指定初始容量和负载因子的空HashMap
     *
     * @param initialCapacity the initial capacity
     * @param loadFactor      the load factor
     * @throws IllegalArgumentException if the initial capacity is negative
     *                                  or the load factor is nonpositive
     */
    public HashMap(int initialCapacity, float loadFactor) {
        //初始容量不能小于0
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                    initialCapacity);
        //初始容量最大为2^30
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        //加载因子不能小于等于0
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                    loadFactor);
        this.loadFactor = loadFactor;
        //扩容阈值，2的n次幂
        this.threshold = tableSizeFor(initialCapacity);
    }

    /**
     * Constructs an empty HashMap with the specified initial
     * capacity and the default load factor (0.75).
     * 构造一个空的HashMap，具有指定的初始容量和缺省负载因子(0.75)。
     *
     * @param initialCapacity the initial capacity.
     * @throws IllegalArgumentException if the initial capacity is negative.
     */
    public HashMap(int initialCapacity) {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }

    /**
     * Constructs an empty HashMap with the default initial capacity
     * (16) and the default load factor (0.75).
     * 构造一个空的HashMap，默认初始容量(16)和默认负载因子(0.75)。
     */
    public HashMap() {
        this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
    }

    /**
     * Constructs a new HashMap with the same mappings as the
     * specified Map.  The HashMap is created with
     * default load factor (0.75) and an initial capacity sufficient to
     * hold the mappings in the specified Map.
     * 使用与指定的Map相同的映射构造一个新的HashMap。
     * 创建HashMap时使用了默认的负载因子(0.75)和足够容纳指定Map中的映射的初始容量。
     *
     * @param m the map whose mappings are to be placed in this map
     * @throws NullPointerException if the specified map is null
     */
    public HashMap(Map<? extends K, ? extends V> m) {
        this.loadFactor = DEFAULT_LOAD_FACTOR;
        putMapEntries(m, false);
    }

    /**
     * Implements Map.putAll and Map constructor
     * 实现了Map.putAl和Map构造函数
     *
     * @param m     the map
     * @param evict false when initially constructing this map, else
     *              true (relayed to method afterNodeInsertion).
     */
    final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {
        int s = m.size();
        if (s > 0) {
            //如果第一次初始化
            if (table == null) { // pre-size
                float ft = ((float) s / loadFactor) + 1.0F;
                int t = ((ft < (float) MAXIMUM_CAPACITY) ?
                        (int) ft : MAXIMUM_CAPACITY);
                if (t > threshold)
                    // 算出阈值
                    threshold = tableSizeFor(t);
            } else if (s > threshold)
                // 需要扩容
                resize();
            for (Entry<? extends K, ? extends V> e : m.entrySet()) {
                K key = e.getKey();
                V value = e.getValue();
                //元素入map
                putVal(hash(key), key, value, false, evict);
            }
        }
    }

    /**
     * Returns the number of key-value mappings in this map.
     * 返回此映射中键值映射的数目。
     * @return the number of key-value mappings in this map
     */
    public int size() {
        return size;
    }

    /**
     * Returns true if this map contains no key-value mappings.
     * 如果此映射不包含键值映射，则返回true
     * @return true if this map contains no key-value mappings
     */
    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * Returns the value to which the specified key is mapped,
     * or {@code null} if this map contains no mapping for the key.
     * 

     * 返回指定键映射到的值，如果此映射不包含键的映射，则返回{@code null}。
     *
     * 
More formally, if this map contains a mapping from a key
     * {@code k} to a value {@code v} such that {@code (key==null ? k==null :
     * key.equals(k))}, then this method returns {@code v}; otherwise
     * it returns {@code null}.  (There can be at most one such mapping.)
     * 

     * 更正式地说，如果这个映射包含一个键{@code k}到一个值{@code v}的映射，
     * 使得{@code (key==null ?k==null: key.equals(k))}，则该方法返回{@code v};
     * 否则返回{@code null}。(最多可以有一个这样的映射。)
     *
     * 
A return value of {@code null} does not necessarily
     * indicate that the map contains no mapping for the key; it's also
     * possible that the map explicitly maps the key to {@code null}.
     * The {@link #containsKey containsKey} operation may be used to
     * distinguish these two cases.
     * 

     * 返回值{@code null}不一定表示映射不包含键的映射;
     * 也有可能映射显式地将键映射到{@code null}。
     * {@link #containsKey containsKey}操作可用于区分这两种情况。
     *
     * @see #put(Object, Object)
     */
    public V get(Object key) {
        //当前节点
        Node<K, V> e;
        //获取当前节点，并返回节点的值
        return (e = getNode(hash(key), key)) == null ? null : e.value;
    }

    /**
     * Implements Map.get and related methods
     * 

     * 获取节点
     *
     * @param hash hash for key
     * @param key  the key
     * @return the node, or null if none
     */
    final Node<K, V> getNode(int hash, Object key) {
        //当前表
        Node<K, V>[] tab;
        Node<K, V> first, e;
        int n;
        K k;
        //如果当前表不为null,且表长度大于0.并且找到桶的位置
        if ((tab = table) != null && (n = tab.length) > 0 &&
                (first = tab[(n - 1) & hash]) != null) {
            //如果第一个就和key相等
            if (first.hash == hash && // always check first node
                    ((k = first.key) == key || (key != null && key.equals(k))))
                //返回桶的第一个元素
                return first;
            //如果第一个节点后面还有接待你
            if ((e = first.next) != null) {
                //如果是红黑树
                if (first instanceof TreeNode)
                    //获取树中的节点
                    return ((TreeNode<K, V>) first).getTreeNode(hash, key);
                //迭代链表，获取匹配的节点
                do {
                    if (e.hash == hash &&
                            ((k = e.key) == key || (key != null && key.equals(k))))
                        return e;
                } while ((e = e.next) != null);
            }
        }
        //没找到，返回null
        return null;
    }

    /**
     * Returns true if this map contains a mapping for the
     * specified key.
     * 如果此映射包含指定键的映射，则返回true。
     *
     * @param key The key whose presence in this map is to be tested
     * @return true if this map contains a mapping for the specified
     * key.
     */
    public boolean containsKey(Object key) {
        return getNode(hash(key), key) != null;
    }

    /**
     * Associates the specified value with the specified key in this map.
     * If the map previously contained a mapping for the key, the old
     * value is replaced.
     * 

     * 将指定值与此映射中的指定键关联。如果映射以前包含键的映射，则替换旧值。
     *
     * @param key   key with which the specified value is to be associated
     * @param value value to be associated with the specified key
     * @return the previous value associated with key, or
     * null if there was no mapping for key.
     * (A null return can also indicate that the map
     * previously associated null with key.)
     */
    public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
    }

    /**
     * Implements Map.put and related methods
     * 实现了 Map.put及其他相关方法
     *
     * @param hash         键的Hash值
     * @param key          键
     * @param value        值
     * @param onlyIfAbsent 如果为真，则不要更改现有值
     * @param evict        如果为false，则该表处于创建模式。
     * @return 老的值，如果没有，则为空
     */
    final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        //当前表
        Node<K, V>[] tab;
        //桶
        Node<K, V> p;
        //n:表长度
        //i:桶在表中的索引
        int n, i;
        //如果当前表为null或者表长度为0
        if ((tab = table) == null || (n = tab.length) == 0)
            //扩容操作,初始化
            n = (tab = resize()).length;
        //如果 键所在的桶 为null
        if ((p = tab[i = (n - 1) & hash]) == null)
            // 新建桶
            tab[i] = newNode(hash, key, value, null);

            //如果 键所在的桶 不为null
        else {
            //当前key节点
            Node<K, V> e;
            K k;
            //确认桶的位置
            if (p.hash == hash &&
                    ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
                //如果是红黑树
            else if (p instanceof TreeNode)
                //红黑树新增节点 后期分析
                e = ((TreeNode<K, V>) p).putTreeVal(this, tab, hash, key, value);
            else {
                //循环
                for (int binCount = 0; ; ++binCount) {
                    //如果桶的下一个节点为null
                    if ((e = p.next) == null) {
                        //创建节点
                        p.next = newNode(hash, key, value, null);
                        //如果大于树化阈值
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            //将链表转为红黑树，后期分析
                            treeifyBin(tab, hash);
                        //跳出循环
                        break;
                    }
                    //在链表中找到了key
                    if (e.hash == hash &&
                            ((k = e.key) == key || (key != null && key.equals(k))))
                        //跳出循环
                        break;
                    p = e;
                }
            }
            //存在key节点
            if (e != null) { // existing mapping for key
                //老的值
                V oldValue = e.value;
                // onlyIfAbsent如果为真，则不要更改现有值
                if (!onlyIfAbsent || oldValue == null)
                    //更改现有值
                    e.value = value;
                //回调
                afterNodeAccess(e);
                //返回旧的值
                return oldValue;
            }
        }
        //修改计数器加一
        ++modCount;
        //判断是否需要扩容
        if (++size > threshold)
            //扩容操作
            resize();
        //回调
        afterNodeInsertion(evict);
        //返回null
        return null;
    }

    /**
     * Initializes or doubles table size.  If null, allocates in
     * accord with initial capacity target held in field threshold.
     * Otherwise, because we are using power-of-two expansion, the
     * elements from each bin must either stay at same index, or move
     * with a power of two offset in the new table.
     * 

     * 初始化或两倍表大小。如果为空，则按照字段阈值中包含的初始容量目标分配。
     * 否则，因为我们使用的是2的幂展开，所以每个桶中的元素必须保持相同的索引，或者在新表中以2的幂偏移量移动。
     *
     * @return the table
     */
    final Node<K, V>[] resize() {
        //老的表，有可能为null
        Node<K, V>[] oldTab = table;
        //获取老的表的长度
        int oldCap = (oldTab == null) ? 0 : oldTab.length;
        //老的扩容阈值
        int oldThr = threshold;
        //新的表长度，扩容阈值
        int newCap, newThr = 0;
        // 老的表长度大于0
        if (oldCap > 0) {
            // 最大的时候，不管理，直接返回
            if (oldCap >= MAXIMUM_CAPACITY) {
                threshold = Integer.MAX_VALUE;
                return oldTab;
            } else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                    oldCap >= DEFAULT_INITIAL_CAPACITY)
                // 新的表长度变为以前老表长度的2倍
                newThr = oldThr << 1; // double threshold
        } else if (oldThr > 0) // initial capacity was placed in threshold
            //如果老的阈值大于0，且老的表长度为0，则新表容量设置为老阈值
            newCap = oldThr;
        else {               // zero initial threshold signifies using defaults
            //初始阈值为零表示使用默认值：16
            newCap = DEFAULT_INITIAL_CAPACITY;
            //扩容阈值：16*0.75
            newThr = (int) (DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
        }
        //如果新的阈值为0，则根据新的表容量计算出。
        if (newThr == 0) {
            float ft = (float) newCap * loadFactor;
            newThr = (newCap < MAXIMUM_CAPACITY && ft < (float) MAXIMUM_CAPACITY ?
                    (int) ft : Integer.MAX_VALUE);
        }
        threshold = newThr;
        // 生成新的数组（表）
        @SuppressWarnings({"rawtypes", "unchecked"})
        Node<K, V>[] newTab = (Node<K, V>[]) new Node[newCap];
        // 使用新表
        table = newTab;
        //如果老表内有数据，则取出来，放到新表中，耗时的操作
        if (oldTab != null) {
            //迭代老的表
            for (int j = 0; j < oldCap; ++j) {
                Node<K, V> e;
                //如果表中桶内容不为null
                if ((e = oldTab[j]) != null) {
                    //清空，help GC
                    oldTab[j] = null;
                    //如果桶中不存在下一个节点
                    if (e.next == null)
                        //将此桶计算hash,重新放入新桶中
                        newTab[e.hash & (newCap - 1)] = e;
                        //如果桶中元素为树形节点
                    else if (e instanceof TreeNode)
                        // 将树仓中的节点拆分为上下树仓，如果太小，则取消树仓。仅从resize调用;
                        // 红黑树这后面专门分析
                        ((TreeNode<K, V>) e).split(this, newTab, j, oldCap);
                    else { // preserve order
                        //是链表结构，且后面有节点，进行链表复制
                        //它并没有重新计算元素在数组中的位置
                        //而是采用了原始位置加原数组长度的方法计算得到位置


                        //位置没有变化的，放到lo
                        Node<K, V> loHead = null, loTail = null;

                        //位置发生变化的，当到hi
                        Node<K, V> hiHead = null, hiTail = null;
                        //下一个节点
                        Node<K, V> next;
                        do {
                            //下一个节点
                            next = e.next;
                            // (e.hash & oldCap) 得到的是 元素的在数组中的位置是否需要移动,示例如下
                            // 示例1：
                            // e.hash=10 0000 1010
                            // oldCap=16 0001 0000
                            //	 &   =0	 0000 0000       比较高位的第一位 0
                            //结论：元素位置在扩容后数组中的位置没有发生改变

                            // 示例2：
                            // e.hash=17 0001 0001
                            // oldCap=16 0001 0000
                            //	 &   =1	 0001 0000      比较高位的第一位   1

                            if ((e.hash & oldCap) == 0) {
                                if (loTail == null)
                                    loHead = e;
                                else
                                    loTail.next = e;
                                loTail = e;
                            } else {
                                if (hiTail == null)
                                    hiHead = e;
                                else
                                    hiTail.next = e;
                                hiTail = e;
                            }
                        } while ((e = next) != null);
                        //元素位置在扩容后数组中的位置没有发生改变
                        if (loTail != null) {
                            loTail.next = null;
                            newTab[j] = loHead;
                        }
                        //元素位置在扩容后数组中的位置发生了改变，新的下标位置是原下标位置+原数组长度
                        if (hiTail != null) {
                            hiTail.next = null;
                            newTab[j + oldCap] = hiHead;
                        }
                    }
                }
            }
        }
        return newTab;
    }

    /**
     * Replaces all linked nodes in bin at index for given hash unless
     * table is too small, in which case resizes instead.
     * 链表转为红黑树，如果容量不够则扩容
     */
    final void treeifyBin(Node<K, V>[] tab, int hash) {
        int n, index;
        Node<K, V> e;
        //如果表为null 或者表容量小于 最小树化容量64
        if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
            //扩容
            resize();
            //确定表中桶的位置，且不为null
        else if ((e = tab[index = (n - 1) & hash]) != null) {
            TreeNode<K, V> hd = null, tl = null;
            do {
                //将链表节点转为红黑树节点
                TreeNode<K, V> p = replacementTreeNode(e, null);
                if (tl == null)
                    hd = p;
                else {
                    p.prev = tl;
                    tl.next = p;
                }
                tl = p;
            } while ((e = e.next) != null);
            if ((tab[index] = hd) != null)
                hd.treeify(tab);
        }
    }

    /**
     * Copies all of the mappings from the specified map to this map.
     * These mappings will replace any mappings that this map had for
     * any of the keys currently in the specified map.
     * 

     * 将指定映射的所有映射复制到此映射。这些映射将替换当前指定映射中任意键的映射。
     *
     * @param m mappings to be stored in this map
     * @throws NullPointerException if the specified map is null
     */
    public void putAll(Map<? extends K, ? extends V> m) {
        putMapEntries(m, true);
    }

    /**
     * Removes the mapping for the specified key from this map if present.
     * 如果存在，则从此映射中删除指定键的映射。
     *
     * @param key key whose mapping is to be removed from the map
     * @return the previous value associated with key, or
     * null if there was no mapping for key.
     * (A null return can also indicate that the map
     * previously associated null with key.)
     */
    public V remove(Object key) {
        Node<K, V> e;
        return (e = removeNode(hash(key), key, null, false, true)) == null ?
                null : e.value;
    }

    /**
     * Implements Map.remove and related methods
     * 删除节点
     *
     * @param hash       hash for key
     * @param key        the key
     * @param value      the value to match if matchValue, else ignored
     * @param matchValue if true only remove if value is equal
     * @param movable    if false do not move other nodes while removing
     * @return the node, or null if none
     */
    final Node<K, V> removeNode(int hash, Object key, Object value,
                                boolean matchValue, boolean movable) {
        Node<K, V>[] tab;
        Node<K, V> p;
        int n, index;
        //表不为空，且定位到桶的位置
        if ((tab = table) != null && (n = tab.length) > 0 &&
                (p = tab[index = (n - 1) & hash]) != null) {
            Node<K, V> node = null, e;
            K k;
            V v;
            //获取到当前节点
            if (p.hash == hash &&
                    ((k = p.key) == key || (key != null && key.equals(k))))
                node = p;
                //如果存在下一个节点
            else if ((e = p.next) != null) {
                //是红黑树
                if (p instanceof TreeNode)
                    node = ((TreeNode<K, V>) p).getTreeNode(hash, key);
                else {
                    //迭代链表
                    do {
                        if (e.hash == hash &&
                                ((k = e.key) == key ||
                                        (key != null && key.equals(k)))) {
                            node = e;
                            break;
                        }
                        p = e;
                    } while ((e = e.next) != null);
                }
            }
            //取到键
            if (node != null && (!matchValue || (v = node.value) == value ||
                    (value != null && value.equals(v)))) {
                if (node instanceof TreeNode)
                    //删除树节点
                    ((TreeNode<K, V>) node).removeTreeNode(this, tab, movable);
                else if (node == p)
                    //链表节点置空
                    tab[index] = node.next;
                else
                    //将节点链接到删除节点的下一个
                    p.next = node.next;
                //修改次数+1
                ++modCount;
                //数量-1
                --size;
                //回调
                afterNodeRemoval(node);
                return node;
            }
        }
        return null;
    }

    /**
     * Removes all of the mappings from this map.
     * The map will be empty after this call returns.
     * 从该映射中删除所有映射。这个调用返回后映射将为空。
     */
    public void clear() {
        Node<K, V>[] tab;
        modCount++;
        if ((tab = table) != null && size > 0) {
            size = 0;
            for (int i = 0; i < tab.length; ++i)
                tab[i] = null;
        }
    }

    /**
     * Returns true if this map maps one or more keys to the
     * specified value.
     * 
     * 如果此映射将一个或多个键映射到指定值，则返回true。
     *
     * @param value value whose presence in this map is to be tested
     * @return true if this map maps one or more keys to the
     * specified value
     */
    public boolean containsValue(Object value) {
        Node<K, V>[] tab;
        V v;
        if ((tab = table) != null && size > 0) {
            for (int i = 0; i < tab.length; ++i) {
                for (Node<K, V> e = tab[i]; e != null; e = e.next) {
                    if ((v = e.value) == value ||
                            (value != null && value.equals(v)))
                        return true;
                }
            }
        }
        return false;
    }
}

红黑树源码

/**
 * Entry for Tree bins. Extends LinkedHashMap.Entry (which in turn
 * extends Node) so can be used as extension of either regular or
 * linked node.
 * 树形桶，继承自LinkedHashMap.Entry（继承自Node），所以能用来做基础的链表操作。
 */
static final class TreeNode<K, V> extends LinkedHashMap.Entry<K, V> {
    // 父节点
    TreeNode<K, V> parent;  // red-black tree
    // 左节点
    TreeNode<K, V> left;
    // 右节点
    TreeNode<K, V> right;
    // 删除后需要断开next链接
    TreeNode<K, V> prev;    // needed to unlink next upon deletion
    //是否为红节点
    boolean red;

    TreeNode(int hash, K key, V val, Node<K, V> next) {
        super(hash, key, val, next);
    }

    /**
     * Returns root of tree containing this node.
     * 返回包含此节点的树的根。
     */
    final TreeNode<K, V> root() {
        //向上迭代，获取到根节点，根节点的父节点为null
        for (TreeNode<K, V> r = this, p; ; ) {
            if ((p = r.parent) == null)
                return r;
            r = p;
        }
    }

    /**
     * Ensures that the given root is the first node of its bin.
     * 确保给定根是其桶的第一个节点。
     * 将根节点转移到树形桶的第一个位置
     */
    static <K, V> void moveRootToFront(Node<K, V>[] tab, TreeNode<K, V> root) {
        int n;
        //root不为空，表不为空
        if (root != null && tab != null && (n = tab.length) > 0) {
            //root在表中的位置（相当于取模）
            int index = (n - 1) & root.hash;
            //获取树形桶第一个节点
            TreeNode<K, V> first = (TreeNode<K, V>) tab[index];
            //如果root引用不是第一个节点
            if (root != first) {
                Node<K, V> rn;
                //root放在第一个索引位置
                tab[index] = root;
                //根节点的前驱
                TreeNode<K, V> rp = root.prev;
                //如果根节点的后继不为空
                if ((rn = root.next) != null)
                    //跟节点后继的前驱指向根节点的前驱
                    ((TreeNode<K, V>) rn).prev = rp;
                //根节点的前驱不为空
                if (rp != null)
                    //根节点后继直接指向前驱
                    rp.next = rn;
                //如果树形桶第一个节点不为空
                if (first != null)
                    //第一个节点的前驱指向根节点
                    first.prev = root;
                //根节点的后继指向first
                root.next = first;
                //根节点的前驱置为null
                root.prev = null;
            }
            assert checkInvariants(root);
        }
    }

    /**
     * Finds the node starting at root p with the given hash and key.
     * The kc argument caches comparableClassFor(key) upon first use
     * comparing keys.
     * 使用给定的散列和键从根p开始查找节点。kc参数在第一次使用比较键时缓存comparableClassFor(key)。
     */
    final TreeNode<K, V> find(int h, Object k, Class<?> kc) {
        TreeNode<K, V> p = this;
        //只要p不为null就一直循环
        do {
            int ph, dir;
            K pk;
            TreeNode<K, V> pl = p.left, pr = p.right, q;
            //如果p的hash 大于 h
            if ((ph = p.hash) > h)
                //向左找
                p = pl;
            else if (ph < h)
                //如果p的hash 大于 h，向右找
                p = pr;
            else if ((pk = p.key) == k || (k != null && k.equals(pk)))
                //找到了，则返回p
                return p;
            else if (pl == null)
                //左边全都遍历结束，找右边的
                p = pr;
            else if (pr == null)
                //右边全都遍历结束，找左边的
                p = pl;
            else if ((kc != null || (kc = comparableClassFor(k)) != null) && (dir = compareComparables(kc, k, pk)) != 0)
                p = (dir < 0) ? pl : pr;
            else if ((q = pr.find(h, k, kc)) != null) //递归调用
                return q;
            else
                p = pl;
        } while (p != null);
        //没找到返回null
        return null;
    }

    /**
     * Calls find for root node.
     * 以根节点调用find。
     */
    final TreeNode<K, V> getTreeNode(int h, Object k) {
        return ((parent != null) ? root() : this).find(h, k, null);
    }

    /**
     * Tie-breaking utility for ordering insertions when equal
     * hashCodes and non-comparable. We don't require a total
     * order, just a consistent insertion rule to maintain
     * equivalence across rebalancings. Tie-breaking further than
     * necessary simplifies testing a bit.
     * 当哈希码相等且不可比较时，用于排序插入的断开连接实用程序。
     * 我们不需要一个总顺序，只需要一个一致的插入规则来在重新平衡之间保持等价。
     * Tie-breaking更能简化测试。
     */
    static int tieBreakOrder(Object a, Object b) {
        //返回与默认方法hashCode()返回的相同的给定对象的散列代码，无论给定对象的类是否覆盖hashCode()。
        int d;
        if (a == null || b == null ||
                (d = a.getClass().getName().
                        compareTo(b.getClass().getName())) == 0)
            d = (System.identityHashCode(a) <= System.identityHashCode(b) ?
                    -1 : 1);
        return d;
    }

    /**
     * Forms tree of the nodes linked from this node.
     * 将链表节点转为树节点
     *
     * @return root of tree 树的根
     */
    final void treeify(Node<K, V>[] tab) {
        TreeNode<K, V> root = null;
        for (TreeNode<K, V> x = this, next; x != null; x = next) {
            //x节点的后继
            next = (TreeNode<K, V>) x.next;
            x.left = x.right = null;

            //如果根节点为空
            if (root == null) {
                //初始化根节点（黑色）
                x.parent = null;
                x.red = false;
                root = x;
            } else {
                //如果根节点非空
                K k = x.key;
                int h = x.hash;
                Class<?> kc = null;

                for (TreeNode<K, V> p = root; ; ) {
                    int dir, ph;
                    K pk = p.key;
                    //找到插入的位置
                    if ((ph = p.hash) > h)
                        dir = -1;
                    else if (ph < h)
                        dir = 1;
                    else if ((kc == null &&
                            (kc = comparableClassFor(k)) == null) ||
                            (dir = compareComparables(kc, k, pk)) == 0)
                        dir = tieBreakOrder(k, pk);

                    TreeNode<K, V> xp = p;
                    if ((p = (dir <= 0) ? p.left : p.right) == null) {
                        x.parent = xp;
                        if (dir <= 0)
                            //插入到左节点
                            xp.left = x;
                        else
                            //插入到右节点
                            xp.right = x;
                        //平衡插入，使红黑树保持其性质
                        root = balanceInsertion(root, x);
                        break;
                    }
                }
            }
        }
        //将根节点转移到树形桶的第一个位置
        moveRootToFront(tab, root);
    }

    /**
     * Returns a list of non-TreeNodes replacing those linked from
     * this node.
     * 将树转为链表
     *
     */
    final Node<K, V> untreeify(HashMap<K, V> map) {
        Node<K, V> hd = null, tl = null;
        for (Node<K, V> q = this; q != null; q = q.next) {
            Node<K, V> p = map.replacementNode(q, null);
            if (tl == null)
                hd = p;
            else
                tl.next = p;
            tl = p;
        }
        return hd;
    }

    /**
     * Tree version of putVal.
     * 树版本的插入
     */
    final TreeNode<K, V> putTreeVal(HashMap<K, V> map, Node<K, V>[] tab,
                                    int h, K k, V v) {
        Class<?> kc = null;
        boolean searched = false;
        //返回包含此节点的树的根
        TreeNode<K, V> root = (parent != null) ? root() : this;
        for (TreeNode<K, V> p = root; ; ) {
            int dir, ph;
            K pk;
            //找到待插入的位置
            if ((ph = p.hash) > h)
                dir = -1;
            else if (ph < h)
                dir = 1;
            else if ((pk = p.key) == k || (k != null && k.equals(pk)))
                //返回插入的节点
                return p;
            else if ((kc == null &&
                    (kc = comparableClassFor(k)) == null) ||
                    (dir = compareComparables(kc, k, pk)) == 0) {
                if (!searched) {
                    TreeNode<K, V> q, ch;
                    searched = true;
                    if (((ch = p.left) != null &&
                            (q = ch.find(h, k, kc)) != null) ||
                            ((ch = p.right) != null &&
                                    (q = ch.find(h, k, kc)) != null))
                        return q;
                }
                dir = tieBreakOrder(k, pk);
            }
            //判断插到哪个位置
            TreeNode<K, V> xp = p;
            if ((p = (dir <= 0) ? p.left : p.right) == null) {
                Node<K, V> xpn = xp.next;
                TreeNode<K, V> x = map.newTreeNode(h, k, v, xpn);
                if (dir <= 0)
                    xp.left = x;
                else
                    xp.right = x;
                xp.next = x;
                x.parent = x.prev = xp;
                if (xpn != null)
                    ((TreeNode<K, V>) xpn).prev = x;
                //将根节点转移到树形桶的第一个位置，平衡插入的节点
                moveRootToFront(tab, balanceInsertion(root, x));
                return null;
            }
        }
    }

    /**
     * Removes the given node, that must be present before this call.
     * This is messier than typical red-black deletion code because we
     * cannot swap the contents of an interior node with a leaf
     * successor that is pinned by "next" pointers that are accessible
     * independently during traversal. So instead we swap the tree
     * linkages. If the current tree appears to have too few nodes,
     * the bin is converted back to a plain bin. (The test triggers
     * somewhere between 2 and 6 nodes, depending on tree structure).
     *
     * 移除此调用之前必须存在的给定节点。
     * 这比典型的红黑删除代码更混乱，因为我们不能使用由“next”指针固定的叶子继承器来交换内部节点的内容，
     * 而“next”指针在遍历过程中是独立可访问的。所以我们交换树的连杆。
     * 如果当前树的节点似乎太少，则将该bin转换回普通bin。
     * （测试根据树结构触发2到6个节点）
     *
     */
    final void removeTreeNode(HashMap<K, V> map, Node<K, V>[] tab,
                              boolean movable) {
        int n;
        if (tab == null || (n = tab.length) == 0)
            return;
        int index = (n - 1) & hash;
        TreeNode<K, V> first = (TreeNode<K, V>) tab[index], root = first, rl;
        TreeNode<K, V> succ = (TreeNode<K, V>) next, pred = prev;
        if (pred == null)
            tab[index] = first = succ;
        else
            pred.next = succ;
        if (succ != null)
            succ.prev = pred;
        if (first == null)
            return;
        if (root.parent != null)
            root = root.root();
        if (root == null || root.right == null ||
                (rl = root.left) == null || rl.left == null) {
            //转为链表
            tab[index] = first.untreeify(map);  // too small
            return;
        }
        TreeNode<K, V> p = this, pl = left, pr = right, replacement;
        if (pl != null && pr != null) {
            TreeNode<K, V> s = pr, sl;
            while ((sl = s.left) != null) // find successor
                s = sl;
            boolean c = s.red;
            s.red = p.red;
            p.red = c; // swap colors
            TreeNode<K, V> sr = s.right;
            TreeNode<K, V> pp = p.parent;
            if (s == pr) { // p was s's direct parent
                p.parent = s;
                s.right = p;
            } else {
                TreeNode<K, V> sp = s.parent;
                if ((p.parent = sp) != null) {
                    if (s == sp.left)
                        sp.left = p;
                    else
                        sp.right = p;
                }
                if ((s.right = pr) != null)
                    pr.parent = s;
            }
            p.left = null;
            if ((p.right = sr) != null)
                sr.parent = p;
            if ((s.left = pl) != null)
                pl.parent = s;
            if ((s.parent = pp) == null)
                root = s;
            else if (p == pp.left)
                pp.left = s;
            else
                pp.right = s;
            if (sr != null)
                replacement = sr;
            else
                replacement = p;
        } else if (pl != null)
            replacement = pl;
        else if (pr != null)
            replacement = pr;
        else
            replacement = p;
        if (replacement != p) {
            TreeNode<K, V> pp = replacement.parent = p.parent;
            if (pp == null)
                root = replacement;
            else if (p == pp.left)
                pp.left = replacement;
            else
                pp.right = replacement;
            p.left = p.right = p.parent = null;
        }
        //平衡删除
        TreeNode<K, V> r = p.red ? root : balanceDeletion(root, replacement);

        if (replacement == p) {  // detach
            TreeNode<K, V> pp = p.parent;
            p.parent = null;
            if (pp != null) {
                if (p == pp.left)
                    pp.left = null;
                else if (p == pp.right)
                    pp.right = null;
            }
        }
        if (movable)
            moveRootToFront(tab, r);
    }

    /**
     * Splits nodes in a tree bin into lower and upper tree bins,
     * or untreeifies if now too small. Called only from resize;
     * see above discussion about split bits and indices.
     *
     * 将树仓中的节点拆分为上下树仓，如果太小，则取消树仓
     * 仅从resize调用;参见上面关于分割位和索引的讨论
     * @param map   the map
     * @param tab   the table for recording bin heads
     * @param index the index of the table being split
     * @param bit   the bit of hash to split on
     */
    final void split(HashMap<K, V> map, Node<K, V>[] tab, int index, int bit) {
        TreeNode<K, V> b = this;
        // Relink into lo and hi lists, preserving order
        TreeNode<K, V> loHead = null, loTail = null;
        TreeNode<K, V> hiHead = null, hiTail = null;
        int lc = 0, hc = 0;
        for (TreeNode<K, V> e = b, next; e != null; e = next) {
            next = (TreeNode<K, V>) e.next;
            e.next = null;
            if ((e.hash & bit) == 0) {
                if ((e.prev = loTail) == null)
                    loHead = e;
                else
                    loTail.next = e;
                loTail = e;
                ++lc;
            } else {
                if ((e.prev = hiTail) == null)
                    hiHead = e;
                else
                    hiTail.next = e;
                hiTail = e;
                ++hc;
            }
        }

        if (loHead != null) {
            if (lc <= UNTREEIFY_THRESHOLD)
                //变成链表
                tab[index] = loHead.untreeify(map);
            else {
                tab[index] = loHead;
                if (hiHead != null) // (else is already treeified)
                    loHead.treeify(tab);
            }
        }
        if (hiHead != null) {
            if (hc <= UNTREEIFY_THRESHOLD)
                //变成链表
                tab[index + bit] = hiHead.untreeify(map);
            else {
                tab[index + bit] = hiHead;
                if (loHead != null)
                    hiHead.treeify(tab);
            }
        }
    }

    /* ------------------------------------------------------------ */
    // Red-black tree methods, all adapted from CLR


    //树的左旋
    static <K, V> TreeNode<K, V> rotateLeft(TreeNode<K, V> root,
                                            TreeNode<K, V> p) {
        TreeNode<K, V> r, pp, rl;
        if (p != null && (r = p.right) != null) {
            if ((rl = p.right = r.left) != null)
                rl.parent = p;
            if ((pp = r.parent = p.parent) == null)
                (root = r).red = false;
            else if (pp.left == p)
                pp.left = r;
            else
                pp.right = r;
            r.left = p;
            p.parent = r;
        }
        return root;
    }

    //右旋
    static <K, V> TreeNode<K, V> rotateRight(TreeNode<K, V> root,
                                             TreeNode<K, V> p) {
        TreeNode<K, V> l, pp, lr;
        if (p != null && (l = p.left) != null) {
            if ((lr = p.left = l.right) != null)
                lr.parent = p;
            if ((pp = l.parent = p.parent) == null)
                (root = l).red = false;
            else if (pp.right == p)
                pp.right = l;
            else
                pp.left = l;
            l.right = p;
            p.parent = l;
        }
        return root;
    }

    /**
     * Balance insertion tree node.
     * 平衡插入后的红黑树
     *
     * @param   键的类型
     * @param   值的类型
     * @param root 根节点
     * @param x    待插入节点
     * @return 返回根节点
     */
    static <K, V> TreeNode<K, V> balanceInsertion(TreeNode<K, V> root, TreeNode<K, V> x) {
        //将插入的节点置为红色
        x.red = true;
        //xp 待插入节点的父节点
        //xpp 待插入节点的祖节点
        //xppl 祖节点的左孩子，左叔叔
        for (TreeNode<K, V> xp, xpp, xppl, xppr; ; ) {
            //  待插入节点的父节点为空，则当前插入的节点为根节点
            if ((xp = x.parent) == null) {
                //置为黑色
                x.red = false;
                return x;
                //如果父节点是黑色的，或者不存在祖节点
            } else if (!xp.red || (xpp = xp.parent) == null)
                //返回根节点
                return root;
            //父节点是祖节点的左孩子
            if (xp == (xppl = xpp.left)) {
                if ((xppr = xpp.right) != null && xppr.red) {
                    xppr.red = false;
                    xp.red = false;
                    xpp.red = true;
                    x = xpp;
                } else {
                    if (x == xp.right) {

                        root = rotateLeft(root, x = xp);
                        xpp = (xp = x.parent) == null ? null : xp.parent;
                    }
                    if (xp != null) {
                        xp.red = false;
                        if (xpp != null) {
                            xpp.red = true;
                            root = rotateRight(root, xpp);
                        }
                    }
                }
            } else {
                //父节点是祖节点的右孩子
                if (xppl != null && xppl.red) {
                    xppl.red = false;
                    xp.red = false;
                    xpp.red = true;
                    x = xpp;
                } else {
                    if (x == xp.left) {
                        root = rotateRight(root, x = xp);
                        xpp = (xp = x.parent) == null ? null : xp.parent;
                    }
                    if (xp != null) {
                        xp.red = false;
                        if (xpp != null) {
                            xpp.red = true;
                            root = rotateLeft(root, xpp);
                        }
                    }
                }
            }
        }
    }

    //看的我脑壳疼，穷举出所有删除后影响的情况，一一解决
    static <K, V> TreeNode<K, V> balanceDeletion(TreeNode<K, V> root,
                                                 TreeNode<K, V> x) {
        for (TreeNode<K, V> xp, xpl, xpr; ; ) {
            if (x == null || x == root)
                return root;
            else if ((xp = x.parent) == null) {
                x.red = false;
                return x;
            } else if (x.red) {
                x.red = false;
                return root;
            } else if ((xpl = xp.left) == x) {
                if ((xpr = xp.right) != null && xpr.red) {
                    xpr.red = false;
                    xp.red = true;
                    root = rotateLeft(root, xp);
                    xpr = (xp = x.parent) == null ? null : xp.right;
                }
                if (xpr == null)
                    x = xp;
                else {
                    TreeNode<K, V> sl = xpr.left, sr = xpr.right;
                    if ((sr == null || !sr.red) &&
                            (sl == null || !sl.red)) {
                        xpr.red = true;
                        x = xp;
                    } else {
                        if (sr == null || !sr.red) {
                            if (sl != null)
                                sl.red = false;
                            xpr.red = true;
                            root = rotateRight(root, xpr);
                            xpr = (xp = x.parent) == null ?
                                    null : xp.right;
                        }
                        if (xpr != null) {
                            xpr.red = (xp == null) ? false : xp.red;
                            if ((sr = xpr.right) != null)
                                sr.red = false;
                        }
                        if (xp != null) {
                            xp.red = false;
                            root = rotateLeft(root, xp);
                        }
                        x = root;
                    }
                }
            } else { // symmetric
                if (xpl != null && xpl.red) {
                    xpl.red = false;
                    xp.red = true;
                    root = rotateRight(root, xp);
                    xpl = (xp = x.parent) == null ? null : xp.left;
                }
                if (xpl == null)
                    x = xp;
                else {
                    TreeNode<K, V> sl = xpl.left, sr = xpl.right;
                    if ((sl == null || !sl.red) &&
                            (sr == null || !sr.red)) {
                        xpl.red = true;
                        x = xp;
                    } else {
                        if (sl == null || !sl.red) {
                            if (sr != null)
                                sr.red = false;
                            xpl.red = true;
                            root = rotateLeft(root, xpl);
                            xpl = (xp = x.parent) == null ?
                                    null : xp.left;
                        }
                        if (xpl != null) {
                            xpl.red = (xp == null) ? false : xp.red;
                            if ((sl = xpl.left) != null)
                                sl.red = false;
                        }
                        if (xp != null) {
                            xp.red = false;
                            root = rotateRight(root, xp);
                        }
                        x = root;
                    }
                }
            }
        }
    }

    /**
     * Recursive invariant check
     * 递归 不变量 检查
     */
    static <K, V> boolean checkInvariants(TreeNode<K, V> t) {
        TreeNode<K, V> tp = t.parent, tl = t.left, tr = t.right,
                tb = t.prev, tn = (TreeNode<K, V>) t.next;
        if (tb != null && tb.next != t)
            return false;
        if (tn != null && tn.prev != t)
            return false;
        if (tp != null && t != tp.left && t != tp.right)
            return false;
        if (tl != null && (tl.parent != t || tl.hash > t.hash))
            return false;
        if (tr != null && (tr.parent != t || tr.hash < t.hash))
            return false;
        if (t.red && tl != null && tl.red && tr != null && tr.red)
            return false;
        if (tl != null && !checkInvariants(tl))
            return false;
        if (tr != null && !checkInvariants(tr))
            return false;
        return true;
    }
}

你可能感兴趣的:(Java学习,java,哈希算法,链表)

Long类型前后端数据不一致 igotyback 前端
响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
LocalDateTime 转 String igotyback java 开发语言
importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类 qt 开发语言 sdl2 linux
需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
DIV+CSS+JavaScript技术制作网页（旅游主题网页设计与制作）云南大理 STU学生网页设计网页设计期末网页作业 html静态网页 html5期末大作业网页设计 web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业：【HTML5网页期末作业(1000套)】程序员有趣的告白方式：【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面：计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
【华为OD机试真题2023B卷 JAVA&JS】We Are A Team 若博豆 java 算法华为 javascript
华为OD2023（B卷）机试题库全覆盖，刷题指南点这里WeAreATeam时间限制：1秒|内存限制：32768K|语言限制：不限题目描述：总共有n个人在机房，每个人有一个标号（1<=标号<=n），他们分成了多个团队，需要你根据收到的m条消息判定指定的两个人是否在一个团队中，具体的：1、消息构成为：abc，整数a、b分别代
关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript 二挡起步 web前端期末大作业 javascript html css 旅游风景
⛵源码获取文末联系✈Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业，Web大学生网页HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
HTML网页设计制作大作业（div+css）云南我的家乡旅游景点带文字滚动二挡起步 web前端期末大作业 web设计网页规划与设计 html css javascript dreamweaver 前端
Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript：做与用户的交互行为文章目录前端学习路线
node.js学习小猿L node.js node.js 学习 vim
node.js学习实操及笔记温故node.js，node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础，三大框架vuereactangular离不开node.jsnode.js是什么官网：node.js是一个开源的、跨平台的运行JavaScript的运行
Java 重写(Override)与重载(Overload) 叨唧唧的
Java重写(Override)与重载(Overload)重写(Override)重写是子类对父类的允许访问的方法的实现过程进行重新编写,返回值和形参都不能改变。即外壳不变，核心重写！重写的好处在于子类可以根据需要，定义特定于自己的行为。也就是说子类能够根据需要实现父类的方法。重写方法不能抛出新的检查异常或者比被重写方法申明更加宽泛的异常。例如：父类的一个方法申明了一个检查异常IOExceptio
简单了解 JVM 记得开心一点啊 jvm
目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称，意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统（如：JVM、VMwave、VirtualBox）。JVM和其他两个虚拟机
1分钟解决 -bash: mvn: command not found，在Centos 7中安装Maven Energet!c 开发语言
1分钟解决-bash:mvn:commandnotfound，在Centos7中安装Maven检查Java环境1下载Maven2解压Maven3配置环境变量4验证安装5常见问题与注意事项6总结检查Java环境Maven依赖Java环境，请确保系统已经安装了Java并配置了环境变量。可以通过以下命令检查：java-version如果未安装，请先安装Java。1下载Maven从官网下载：前往Apach
Java企业面试题3 马龙强_ java
1.break和continue的作用(智*图)break：用于完全退出一个循环（如for,while）或一个switch语句。当在循环体内遇到break语句时，程序会立即跳出当前循环体，继续执行循环之后的代码。continue：用于跳过当前循环体中剩余的部分，并开始下一次循环。如果是在for循环中使用continue，则会直接进行条件判断以决定是否执行下一轮循环。2.if分支语句和switch分
JVM、JRE和 JDK：理解Java开发的三大核心组件 Y雨何时停T Java java
Java是一门跨平台的编程语言，它的成功离不开背后强大的运行环境与开发工具的支持。在Java的生态中，JVM（Java虚拟机）、JRE（Java运行时环境）和JDK（Java开发工具包）是三个至关重要的核心组件。本文将探讨JVM、JDK和JRE的区别，帮助你更好地理解Java的运行机制。1.JVM：Java虚拟机（JavaVirtualMachine）什么是JVM？JVM，即Java虚拟机，是Ja
Java面试题精选：消息队列(二) 芒果不是芒 Java面试题精选 java kafka
一、Kafka的特性1.消息持久化：消息存储在磁盘，所以消息不会丢失2.高吞吐量：可以轻松实现单机百万级别的并发3.扩展性：扩展性强，还是动态扩展4.多客户端支持：支持多种语言（Java、C、C++、GO、）5.KafkaStreams（一个天生的流处理）:在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制：Kafka进行生产或者消费的时候会
2024.8.22 Python，链表两数之和，链表快速反转，二叉树的深度，二叉树前中后序遍历，N叉树递归遍历，翻转二叉树 RaidenQ python 链表开发语言
1.链表两数之和输入：l1=[2,4,3],l2=[5,6,4]输出：[7,0,8]解释：342+465=807.示例2：输入：l1=[0],l2=[0]输出：[0]示例3：输入：l1=[9,9,9,9,9,9,9],l2=[9,9,9,9]输出：[8,9,9,9,0,0,0,1]昨天的这个题，用自己的办法写的麻烦的要死，然后刚才一看chat归类的办法，感觉自己像个智障。classListNode
白骑士的Java教学基础篇 2.5 控制流语句白骑士所长 Java 教学 java 开发语言
欢迎继续学习Java编程的基础篇！在前面的章节中，我们了解了Java的变量、数据类型和运算符。接下来，我们将探讨Java中的控制流语句。控制流语句用于控制程序的执行顺序，使我们能够根据特定条件执行不同的代码块，或重复执行某段代码。这是编写复杂程序的基础。通过学习这一节内容，你将掌握如何使用条件语句和循环语句来编写更加灵活和高效的代码。条件语句条件语句用于根据条件的真假来执行不同的代码块。if语句‘
python语法——三目运算符 HappyRocking python python 三目运算符
在java中，有三目运算符，如：intc=(a>b)?a:b表示c取两者中的较大值。但是在python，不能直接这样使用，估计是因为冒号在python有分行的关键作用。那么在python中，如何实现类似功能呢？可以使用ifelse语句，也是一行可以完成，格式为：aifbelsec表示如果b为True，则表达式等于a，否则等于c。如：c=(aif(a>b)elseb)同样是完成了取最大值的功能。
[Python] 数据结构详解及代码 AIAdvocate 算法 python 数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
ArrayList 源码解析程序猿进阶 Java基础 ArrayList List java 面试性能优化架构设计 idea
ArrayList是Java集合框架中的一个动态数组实现，提供了可变大小的数组功能。它继承自AbstractList并实现了List接口，是顺序容器，即元素存放的数据与放进去的顺序相同，允许放入null元素，底层通过数组实现。除该类未实现同步外，其余跟Vector大致相同。每个ArrayList都有一个容量capacity，表示底层数组的实际大小，容器内存储元素的个数不能多于当前容量。当向容器中添
Java爬虫框架（一）--架构设计狼图腾-狼之传说 java 框架 java 任务 html解析器存储电子商务
一、架构图那里搜网络爬虫框架主要针对电子商务网站进行数据爬取，分析，存储，索引。爬虫：爬虫负责爬取，解析，处理电子商务网站的网页的内容数据库：存储商品信息索引：商品的全文搜索索引Task队列：需要爬取的网页列表Visited表：已经爬取过的网页列表爬虫监控平台：web平台可以启动，停止爬虫，管理爬虫，task队列，visited表。二、爬虫1.流程1)Scheduler启动爬虫器，TaskMast
Java：爬虫框架 dingcho Java java 爬虫
一、ApacheNutch2【参考地址】Nutch是一个开源Java实现的搜索引擎。它提供了我们运行自己的搜索引擎所需的全部工具。包括全文搜索和Web爬虫。Nutch致力于让每个人能很容易,同时花费很少就可以配置世界一流的Web搜索引擎.为了完成这一宏伟的目标,Nutch必须能够做到:每个月取几十亿网页为这些网页维护一个索引对索引文件进行每秒上千次的搜索提供高质量的搜索结果简单来说Nutch支持分
python怎么将png转为tif_png转tif weixin_39977276
发国外的文章要求图片是tif，cmyk色彩空间的。大小尺寸还有要求。比如网上大神多，找到了一段代码，感谢！https://www.jianshu.com/p/ec2af4311f56https://github.com/KevinZc007/image2Tifimportjava.awt.image.BufferedImage;importjava.io.File;importjava.io.Fi
JavaScript 中，深拷贝（Deep Copy）和浅拷贝（Shallow Copy）跳房子的前端前端面试 javascript 开发语言 ecmascript
在JavaScript中，深拷贝（DeepCopy）和浅拷贝（ShallowCopy）是用于复制对象或数组的两种不同方法。了解它们的区别和应用场景对于避免潜在的bugs和高效地处理数据非常重要。以下是对深拷贝和浅拷贝的详细解释，包括它们的概念、用途、优缺点以及实现方式。1.浅拷贝（ShallowCopy）概念定义：浅拷贝是指创建一个新的对象或数组，其中包含了原对象或数组的基本数据类型的值和对引用数
JAVA·一个简单的登录窗口 MortalTom java 开发语言学习
文章目录概要整体架构流程技术名词解释技术细节资源概要JavaSwing是Java基础类库的一部分，主要用于开发图形用户界面（GUI）程序整体架构流程新建项目，导入sql.jar包（链接放在了文末），编译项目并运行技术名词解释一、特点丰富的组件提供了多种可视化组件，如按钮（JButton）、文本框（JTextField）、标签（JLabel）、下拉列表（JComboBox）等，可以满足不同的界面设计
WebMagic：强大的Java爬虫框架解析与实战 Aaron_945 Java java 爬虫开发语言
文章目录引言官网链接WebMagic原理概述基础使用1.添加依赖2.编写PageProcessor高级使用1.自定义Pipeline2.分布式抓取优点结论引言在大数据时代，网络爬虫作为数据收集的重要工具，扮演着不可或缺的角色。Java作为一门广泛使用的编程语言，在爬虫开发领域也有其独特的优势。WebMagic是一个开源的Java爬虫框架，它提供了简单灵活的API，支持多线程、分布式抓取，以及丰富的
博客网站制作教程 2401_85194651 java maven
首先就是技术框架：后端：Java+SpringBoot数据库：MySQL前端：Vue.js数据库连接：JPA(JavaPersistenceAPI)1.项目结构blog-app/├──backend/│├──src/main/java/com/example/blogapp/││├──BlogApplication.java││├──config/│││└──DatabaseConfig.java
00. 这里整理了最全的爬虫框架（Java + Python）有一只柴犬爬虫系列爬虫 java python
目录1、前言2、什么是网络爬虫3、常见的爬虫框架3.1、java框架3.1.1、WebMagic3.1.2、Jsoup3.1.3、HttpClient3.1.4、Crawler4j3.1.5、HtmlUnit3.1.6、Selenium3.2、Python框架3.2.1、Scrapy3.2.2、BeautifulSoup+Requests3.2.3、Selenium3.2.4、PyQuery3.2
JAVA学习笔记之23种设计模式学习 victorfreedom Java技术设计模式 android java 常用设计模式
博主最近买了《设计模式》这本书来学习，无奈这本书是以C++语言为基础进行说明，整个学习流程下来效率不是很高，虽然有的设计模式通俗易懂，但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番，发现有大神写过了这方面的问题，于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类：创建型模式，共五种：工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式，共七种：适配器
JavaScript `Map` 和 `WeakMap`详细解释跳房子的前端 JavaScript 原生方法 javascript 前端开发语言
在JavaScript中，Map和WeakMap都是用于存储键值对的数据结构，但它们有一些关键的不同之处。MapMap是一种可以存储任意类型的键值对的集合。它保持了键值对的插入顺序，并且可以通过键快速查找对应的值。Map提供了一些非常有用的方法和属性来操作这些数据对：set(key,value):将一个键值对添加到Map中。如果键已经存在，则更新其对应的值。get(key):获取指定键的值。如果键
自定义队列 junjun2018
队列：像排队吃饭一样，先到的先点菜，后来的后点菜。以下代码展示使用单向列表实现的队列。//链表是以节点为单位的，对于单向链表，每个节点中包含一个值和指向下一个对象的引用publicclassNode{Objectvalue;Nodenext;publicNode(Objectvalue){this.value=value;}publicObjectgetValue(){returnvalue;}p
二分查找排序算法周凡杨 java 二分查找排序算法折半
一：概念二分查找又称折半查找（折半搜索/ 二分搜索），优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步
java中的BigDecimal bijian1013 java BigDecimal
在项目开发过程中出现精度丢失问题，查资料用BigDecimal解决，并发现如下这篇BigDecimal的解决问题的思路和方法很值得学习，特转载。原文地址：http://blog.csdn.net/ugg/article/de
Shell echo命令详解 daizj echo shell
Shell echo命令 Shell 的 echo 指令与 PHP 的 echo 指令类似，都是用于字符串的输出。命令格式： echo string 您可以使用echo实现更复杂的输出格式控制。 1.显示普通字符串: echo "It is a test" 这里的双引号完全可以省略，以下命令与上面实例效果一致： echo Itis a test 2.显示转义
Oracle DBA 简单操作周凡杨 oracle dba sql
--执行次数多的SQL select sql_text,executions from ( select sql_text,executions from v$sqlarea order by executions desc ) where rownum<81; &nb
画图重绘朱辉辉33 游戏
我第一次接触重绘是编写五子棋小游戏的时候，因为游戏里的棋盘是用线绘制的，而这些东西并不在系统自带的重绘里，所以在移动窗体时，棋盘并不会重绘出来。所以我们要重写系统的重绘方法。在重写系统重绘方法时，我们要注意一定要调用父类的重绘方法，即加上super.paint(g)，因为如果不调用父类的重绘方式，重写后会把父类的重绘覆盖掉，而父类的重绘方法是绘制画布，这样就导致我们
线程之初体验西蜀石兰线程
一直觉得多线程是学Java的一个分水岭，懂多线程才算入门。之前看《编程思想》的多线程章节，看的云里雾里，知道线程类有哪几个方法，却依旧不知道线程到底是什么？书上都写线程是进程的模块，共享线程的资源，可是这跟多线程编程有毛线的关系，呜呜。。。线程其实也是用户自定义的任务，不要过多的强调线程的属性，而忽略了线程最基本的属性。你可以在线程类的run()方法中定义自己的任务，就跟正常的Ja
linux集群互相免登陆配置林鹤霄 linux
配置ssh免登陆 1、生成秘钥和公钥 ssh-keygen -t rsa 2、提示让你输入，什么都不输，三次回车之后会在~下面的.ssh文件夹中多出两个文件id_rsa 和 id_rsa.pub 其中id_rsa为秘钥，id_rsa.pub为公钥，使用公钥加密的数据只有私钥才能对这些数据解密 c
mysql : Lock wait timeout exceeded; try restarting transaction aigo mysql
原文：http://www.cnblogs.com/freeliver54/archive/2010/09/30/1839042.html 原因是你使用的InnoDB 表类型的时候, 默认参数:innodb_lock_wait_timeout设置锁等待的时间是50s, 因为有的锁等待超过了这个时间,所以抱错. 你可以把这个时间加长,或者优化存储
Socket编程基本的聊天实现。 alleni123 socket
public class Server { //用来存储所有连接上来的客户 private List<ServerThread> clients; public static void main(String[] args) { Server s = new Server(); s.startServer(9988); } publi
多线程监听器事件模式(一个简单的例子) 百合不是茶线程监听模式
多线程的事件监听器模式监听器时间模式经常与多线程使用,在多线程中如何知道我的线程正在执行那什么内容,可以通过时间监听器模式得到创建多线程的事件监听器模式思路: 1, 创建线程并启动,在创建线程的位置设置一个标记 2,创建队
spring InitializingBean接口 bijian1013 java spring
spring的事务的TransactionTemplate，其源码如下： public class TransactionTemplate extends DefaultTransactionDefinition implements TransactionOperations, InitializingBean{ ... } TransactionTemplate继承了DefaultT
Oracle中询表的权限被授予给了哪些用户 bijian1013 oracle 数据库权限
Oracle查询表将权限赋给了哪些用户的SQL，以备查用。 select t.table_name as "表名", t.grantee as "被授权的属组", t.owner as "对象所在的属组"
【Struts2五】Struts2 参数传值 bit1129 struts2
Struts2中参数传值的3种情况 1.请求参数绑定到Action的实例字段上 2.Action将值传递到转发的视图上 3.Action将值传递到重定向的视图上一、请求参数绑定到Action的实例字段上以及Action将值传递到转发的视图上 Struts可以自动将请求URL中的请求参数或者表单提交的参数绑定到Action定义的实例字段上，绑定的规则使用ognl表达式语言
【Kafka十四】关于auto.offset.reset[Q/A] bit1129 kafka
I got serveral questions about auto.offset.reset. This configuration parameter governs how consumer read the message from Kafka when there is no initial offset in ZooKeeper or
nginx gzip压缩配置 ronin47 nginx gzip 压缩范例
nginx gzip压缩配置更多 0 nginx gzip 配置随着nginx的发展，越来越多的网站使用nginx，因此nginx的优化变得越来越重要，今天我们来看看nginx的gzip压缩到底是怎么压缩的呢？ gzip(GNU-ZIP)是一种压缩技术。经过gzip压缩后页面大小可以变为原来的30%甚至更小，这样，用
java-13.输入一个单向链表，输出该链表中倒数第 k 个节点 bylijinnan java
two cursors. Make the first cursor go K steps first. /* * 第 13 题：题目：输入一个单向链表，输出该链表中倒数第 k 个节点 */ public void displayKthItemsBackWard(ListNode head,int k){ ListNode p1=head,p2=head;
Spring源码学习-JdbcTemplate queryForObject bylijinnan java spring
JdbcTemplate中有两个可能会混淆的queryForObject方法： 1. Object queryForObject(String sql, Object[] args, Class requiredType) 2. Object queryForObject(String sql, Object[] args, RowMapper rowMapper) 第1个方法是只查
[冰川时代]在冰川时代,我们需要什么样的技术? comsci 技术
看美国那边的气候情况....我有个感觉...是不是要进入小冰期了? 那么在小冰期里面...我们的户外活动肯定会出现很多问题...在室内呆着的情况会非常多...怎么在室内呆着而不发闷...怎么用最低的电力保证室内的温度.....这都需要技术手段... &nb
js 获取浏览器型号 cuityang js 浏览器
根据浏览器获取iphone和apk的下载地址 <!DOCTYPE html> <html> <head> <meta charset="utf-8" content="text/html"/> <meta name=
C# socks5详解转 dalan_123 socket C#
http://www.cnblogs.com/zhujiechang/archive/2008/10/21/1316308.html 这里主要讲的是用.NET实现基于Socket5下面的代理协议进行客户端的通讯，Socket4的实现是类似的，注意的事，这里不是讲用C#实现一个代理服务器，因为实现一个代理服务器需要实现很多协议，头大，而且现在市面上有很多现成的代理服务器用，性能又好，
运维 Centos问题汇总 dcj3sjt126com 云主机
一、sh 脚本不执行的原因 sh脚本不执行的原因只有2个 1.权限不够 2.sh脚本里路径没写完整。二、解决You have new mail in /var/spool/mail/root 修改/usr/share/logwatch/default.conf/logwatch.conf配置文件 MailTo = MailFrom 三、查询连接数
Yii防注入攻击笔记 dcj3sjt126com sql WEB安全 yii
网站表单有注入漏洞须对所有用户输入的内容进行个过滤和检查，可以使用正则表达式或者直接输入字符判断，大部分是只允许输入字母和数字的，其它字符度不允许；对于内容复杂表单的内容，应该对html和script的符号进行转义替换：尤其是<,>,',"",&这几个符号这里有个转义对照表： http://blog.csdn.net/xinzhu1990/articl
MongoDB简介[一] eksliang mongodb MongoDB简介
MongoDB简介转载请出自出处：http://eksliang.iteye.com/blog/2173288 1.1易于使用 MongoDB是一个面向文档的数据库，而不是关系型数据库。与关系型数据库相比，面向文档的数据库不再有行的概念，取而代之的是更为灵活的“文档”模型。另外，不
zookeeper windows 入门安装和测试 greemranqq zookeeper 安装分布式
一、序言以下是我对zookeeper 的一些理解： zookeeper 作为一个服务注册信息存储的管理工具，好吧，这样说得很抽象，我们举个“栗子”。栗子1号：假设我是一家KTV的老板，我同时拥有5家KTV，我肯定得时刻监视
Spring之使用事务缘由(2-注解实现) ihuning spring
Spring事务注解实现 1. 依赖包： 1.1 spring包： spring-beans-4.0.0.RELEASE.jar spring-context-4.0.0.
iOS App Launch Option 啸笑天 option
iOS 程序启动时总会调用application:didFinishLaunchingWithOptions:，其中第二个参数launchOptions为NSDictionary类型的对象，里面存储有此程序启动的原因。 launchOptions中的可能键值见UIApplication Class Reference的Launch Options Keys节。 1、若用户直接
jdk与jre的区别（_） macroli java jvm jdk
简单的说JDK是面向开发人员使用的SDK，它提供了Java的开发环境和运行环境。SDK是Software Development Kit 一般指软件开发包，可以包括函数库、编译程序等。 JDK就是Java Development Kit JRE是Java Runtime Enviroment是指Java的运行环境，是面向Java程序的使用者，而不是开发者。如果安装了JDK，会发同你
Updates were rejected because the tip of your current branch is behind qiaolevip 学习永无止境每天进步一点点众观千象 git
$ git push joe prod-2295-1 To [email protected]:joe.le/dr-frontend.git ! [rejected] prod-2295-1 -> prod-2295-1 (non-fast-forward) error: failed to push some refs to '[email protected]
[一起学Hive]之十四-Hive的元数据表结构详解 superlxw1234 hive hive元数据结构
关键字：Hive元数据、Hive元数据表结构之前在 “[一起学Hive]之一–Hive概述，Hive是什么”中介绍过，Hive自己维护了一套元数据，用户通过HQL查询时候，Hive首先需要结合元数据，将HQL翻译成MapReduce去执行。本文介绍一下Hive元数据中重要的一些表结构及用途，以Hive0.13为例。文章最后面，会以一个示例来全面了解一下，
Spring 3.2.14，4.1.7，4.2.RC2发布 wiselyman Spring 3
Spring 3.2.14、4.1.7及4.2.RC2于6月30日发布。其中Spring 3.2.1是一个维护版本(维护周期到2016-12-31截止)，后续会继续根据需求和bug发布维护版本。此时，Spring官方强烈建议升级Spring框架至4.1.7 或者将要发布的4.2 。其中Spring 4.1.7主要包含这些更新内容。