开关电源基础02:基本开关电源拓扑(1)-BUCK拓扑
说在开头:关于海森堡的矩阵(1)
我们前面说了,海森堡和泡利到了哥本哈根跟着玻尔混,在哥本哈根海森堡感到了一种竞争的气氛:他在德国少年得志,是出了名的天才,现在突然发现身边的每一个人都毫不逊色。当然,哥本哈根的自由精神和学术氛围在全欧洲都是无与伦比的,而这一切都和尼尔斯.玻尔这位量子论“教父” 密切相关。毫无疑问,在哥本哈根的每一个人都是天才,但他们却都更好的衬托出玻尔本人的伟大来。这位和蔼的丹麦人对每个人都报以善意的微笑,并引导人们畅所欲言,探讨一切类型的问题,人们像众星捧月般的围绕在他身边,个个都为他的学识和人格所折服,海森堡也不例外,而且他将成为玻尔最亲密的学生和朋友之一。
玻尔常常邀请海森堡去他家分享好酒,或则到研究所后面的树林里去散步并讨论学术问题。他是一个极富哲学气质的人,对于许多物理问题的看法都带有深深的哲学色彩,这令海森堡相当震撼,并在很大程度上影响了他本人的思维方式。泡利后来说:他很高兴海森堡在哥本哈根学到了一点哲学。那时有一种思潮在哥本哈根流行开来:物理学的研究对象应该只是能够被观察到、被实践到的事物,物理学只能够从这些东西出发,而不是建立在观察不到或则纯粹是推论的事物上。这个观点对海森堡以及泡利都有很大的影响,海森堡开始隐约感觉到玻尔的旧原子模型里的有些东西似乎不大对头,似乎他们不都是直接能够为实验所探测的。最明显的就是电子的“轨道”以及它绕着轨道运转的频率。
1925年4月27日,海森堡结束了哥本哈根的访问回到了哥廷根,开始重新着手研究氢原子的谱线问题。一开始兴致勃勃地按照玻尔的BKS思路来搞,虽然BKS实在不靠谱但在色散理论中被证明是有效的,海森堡相信这个思路应该可以解决玻尔体系中的一些问题,结果发现它所遇到的数学困难几乎不可克服:障碍实在太大了,不得不放弃原先的计划。无奈之下海森堡决定换一种办法,暂时不考虑谱线强度,而是先从电子在原子中的运动出发,建立其基本的运动模型。
海森堡回到哥廷根后,很快打喷嚏、咳嗽、流鼻涕(一键三连),浑身难受,如果在新冠初期的话那就要先抓起来核酸和隔离,闹了半天他是患了枯草热(过敏性鼻炎),最后决定躲到北海的一个小岛上去远离过敏源,可以肯定的是这个岛上全是石头和沙子,没有花花草草。既然出来度假了,那就好好放松放松,白天海里游泳,晚上读读诗歌,剩下的时间用来思考物理。海森堡吹着海风,小宇宙突然爆发了,禁不住想:玻尔和索末菲老师说电子绕着原子核做圈圈运动,索末菲老师还假设电子的轨道是椭圆的,那他们哪只眼睛看到了?不能观测的东西,那就根本不能当回事!有什么实验证据能证明电子是那样运动的?sigh~
海森堡决定抛开圆轨道的概念,开始了另外一条道路的探索。首先他要先画个表格来统计一下能级;举个栗子:坐公交或则地铁是分段计价的,就是一大张根据起点和终点的表格。海森堡觉得电子跳来跳去,总要有不同的能级,道理跟坐公交车是一样样的。从这个能级跳到那个能级,会放出什么光的频率,需要将这个表格放进公式里计算:一张动量表格乘上一张位置表格;不过表格跟表格之间怎么相乘呢?海森堡没办法,自己推导吧,最后推导出来表格之间的乘法运算,他发明的表格乘法有一个奇怪的特性,那就是不符合乘法交换律:A x B跟B x A结果不一样,为什么怎么会这样?上过线性代数的同学,应该都学过矩阵的乘法,但是海森堡没学过~,海森堡当时完全不知道有这么一门学科,但天才就是天才,他自己发明了矩阵的乘法。除了乘法不满足乘法律之外,对于其它的海森堡都很满意。在他的这一对表格计算里面,自然而然出现了不连续的状况,不需要玻尔硬性规定轨道的不连续,而且海森堡尽量少用假想出来的东西(圆轨道之类),参与计算的这些物理量(能级差)都是可测量的。
圆轨道?在哪里?我没看到啊,海森堡最满意这一点了:每一条频率为f![]() 的光谱线,只能代表两个能级之间的能量差;我们直接观察到的既不是E1也不是E2,而是E1-E2;即,只有能级差或则轨道差是可以被直接观察到的,而能级和圆轨道却不是!海森堡的表格和玻尔的不同,它没有做任何假设和推论,不包含任何不可观察的数据,但作为代价,它采纳了一种二维的庞大结构,每个数据都要用横坐标和纵坐标两个变量来表示。这篇论文后来被人们称为“一个人的文章”,毕竟这是海森堡一个人闷着头写的,这是量子论史上里程碑式的伟大篇章。(参考自:吴京平-无中生有的世界)
的光谱线,只能代表两个能级之间的能量差;我们直接观察到的既不是E1也不是E2,而是E1-E2;即,只有能级差或则轨道差是可以被直接观察到的,而能级和圆轨道却不是!海森堡的表格和玻尔的不同,它没有做任何假设和推论,不包含任何不可观察的数据,但作为代价,它采纳了一种二维的庞大结构,每个数据都要用横坐标和纵坐标两个变量来表示。这篇论文后来被人们称为“一个人的文章”,毕竟这是海森堡一个人闷着头写的,这是量子论史上里程碑式的伟大篇章。(参考自:吴京平-无中生有的世界)
- 降压型(BUCK)拓扑
通过对上一章电源转换器历史的学习,胖友们已经知道了要提升电源转换效率,必须使电源转换器本身的消耗尽量小:1,晶体管要工作在放大区改成工作在饱和区(开关状态);2,为了防止电容器浪涌电流而将串联的电阻器改成电感器。
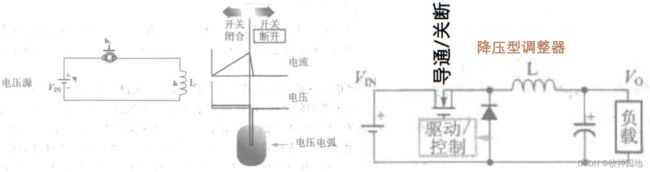
虽然改用电感器后解决了电源转换器效率的问题,但又引入了新的问题:如下左图所示,在“开关”断开的瞬间电感器会导致高压电弧;如此我们便成功地将电容器的“浪涌电流”问题变成了电感器“高压电弧”问题。一顿操作猛如虎,好像也没变好嘛,但现在我们只能一条路走到黑,想一想怎么解决这个高压电弧的问题呢?
“开关”关断时出现感应电压尖峰的原因是:先前流过电感器的电流不能中断,需要续流回路,但又无路可走。所以电流自然地想要去突破电路中的“薄弱点”,即在“开关”、电感器甚至在相邻电路中产生“电弧”来续流。但如果我们有意识的在电路中提供续流回路,那么“开关”关断时的电感器电流就无序流过开关,而由续流回路续流,这样就不会出现问题;电感器也不会以“高压电弧”的形式来泄放。于是产生了降压电源拓扑,如上右图所示。
1,降压型(BUCK)拓扑原理
如下图所示为降压型(BUCK)电源拓扑的结构示意图,具体组成结构如下:
1. 其中Q1为“开关”(MOS管)串接在Vdc电源上,D1为续流二极管串接在GND上,L0为电感器与C0电容器形成LC滤波,保持输出电源电压Vo稳定;
—— Q1,D1,L0和C0器件是BUCK电源电路的功率器件,构成了开关电源拓扑的主体。
2. 采样电阻R1和R2负责输出电压Vo的检测,并将其输入误差放大器(EA)并与参考电压Vref进行比较;
——Vref需要稳定的供电电源,所以有些电源控制器需要一个工作电源(例如:+5V),用于提供稳定的参考电压。
3. 被放大的误差电压Vea被输入到脉宽调整放大器PWM;
4. PWM脉冲输入并以负反馈方式控制Q1的通断。
电源拓扑结构是一个负反馈的电路系统:对输出电源电压(Vo)采样(R1和R2)并与标准参考电压(Vref)进行比较,如果输出采样电压与参考电压不等,那么需要改变“开关”的打开时间Ton,以响应输出电源电压的变化,从而形成一个闭环负反馈,达到稳态。
——我们看到的开关电源系统:输入是Vin,输出是Vout;但是对于电源环路来说Vout是输出(电源拓扑的目的就是输出一个设定的、稳定的电源电压),但Vin并非是输入,真正的输入是Vref,所以在一定范围内的输入电压(Vin)或则其变化时还能保持稳定的输出电压。(后续《环路稳定性》章节具体分析)
如下图为BUCK电源拓扑电路中不同位置的信号波形,我们可以通过观察它们的状态来更深入理解BUCK电源拓扑的工作过程:
1. 在Q1导通时(Ton):V1电压(b)上升为Vdc,此时D1截止,电流方向如绿色线所示:Vdc经过Q1(MOS管)和L0(电感器)输出到C0(输出电容器)和负载;Vo电压(d)缓慢上升。
——电源Vdc给电感器L1“充电”,并对负载和C0(输出电容)供电;此时电感器L0两端电压为Vdc-Vo,且电感器电流线性增加(V=L*dI/dt),所以在负载电流Io不变的情况下,输出电压Vo必然线性增加,可以看成“剩余电流”(电感器电流IL-负载电流Io,即:纹波电流)对电容C0的充电操作。
2. 在Q1关断时(Toff),电感器L0由于电流必须连续,继续正向大电流,V1电压(b)迅速下降直至0V(理想D1导通电压为0V),此时二极管D1导通,电流方向如橙色线所示:GND经过D1和L0 输出到负载;Vo电压(d)缓慢减小。
——粗一看电流是从低电压(GND)的地方流向高电压(Vo),感觉这不科学啊,其实这非常地科学:在Ton时通过电感器L0储存了能量,此时是将能量释放出来,所以可将电感器L0看成是一个电源(有感应电压,具体请复习:《电感器原理》章节);对于电感器L0来说此时外加了一个-Vo的电压,所以经过电感器L0的电流必然线性减小,在负载电流需求不变的情况下,输出电压Vo必然线性减小,同时还需要输出电容器C0也向负载提供一部分电能。
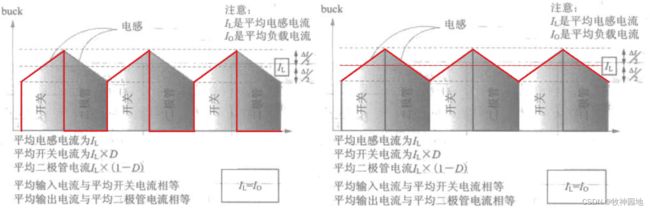
3. 输入电容器串联的是开关管(MOS管),所以输入电容器的电流是斩波式(电流变化非常大)的,如下左图红色线所示,必然会影响输入电源的波动;
——BUCK电源输入电容器,我们一般选择uF级别陶瓷电容,且尽量靠近输入电源管脚。
4. 输出电容器串联的是电感器,所以输出电容电流相对来说是“平滑”的,稳态时负载电流Io是直流,所以并不会流入/流出输出电容器,而流经输出电容器的电流是:纹波电流;纹波电流一般设置负载电流Io的40%,即基于Io的±20%。如上右图所示。
——电感器电流最大值为1.2*Io,考虑降额一般选择1.5*Io电流值为电感器的额定工作电流。
5. 由于负载电流Io需求突发减小,导致输出电压Vo上升,那么通过R1/R2的反馈电压增加,误差放大器输出电压Vea(a)减小,脉宽调制器输出的高电平占比(c)将下降,反馈控制Q1导通时间(b)减少,从而降低输出电压Vo;
6. 反之Vo下降,那么误差放大器输出电压Vea(a)增大,脉冲调制器输出高电平占比(c)上升,控制Q1导通时间(b)增加,从而提升输出电压Vo;形成负反馈机制,保证输出电压稳定。
如果是输入电源电压Vdc的突变是否会影响输出呢?
按照现在原理来说输入电源电压Vdc增加,但是开关占空比不变(占空比是对输出电压的监控,而非输入电压),所以自然导致了输出电压的同步抬升,然后由输出电压的变化再反馈调整占空比。但事实并非如此,主要是Vt是随输入电源电压波动的,所以当输入电源电压Vdc变大,那么PWM波的斜率会变大(更陡峭),所以占空比会随输入电压Vdc成比例增加,从而保持输出的稳定,如下图所示。(具体后续《环路稳定性》专题详细分析)
现在考虑在稳态时各器件的导通损耗,根据伏秒定律分析降压拓扑:Von= Vin – Vsw -Vo,Voff= Vo-(-Vd)=Vo + Vd,Von* Ton = Voff *Toff;可得到占空比D = (Vo+Vd)/(Vin+Vd+Vsw),二极管以及MOS管的压降相对于输入/输出电压比较小,所以可以简化为:D = Vo/Vin;输出电压与输入电压之间的关系为:Vo = Vin * D。
2,“开关”占空比的问题
上一节我们通过伏秒定律推理出来了:BUCK电源的占空比与输入电源电压Vin和输出电源电压Vo的比例相关,即D ≈Vo/Vin。但是占空比居然跟负载电流Io无关,这就让我有些费解:输入电源Vdc通过电感器L0(电感器两端电压同样为:Vdc-Vo)传输能量,按理来说在同样Ton时间内,输送的能量都是一样的,而不同负载电流的开关电源传输能量并不一样,所以Ton应该随负载电流变化才对。而实际上BUCK电源在不同输出电流情况下的占空比,却大致一样(不同负载电流的电源转换效率不同,导致的占空比不同)。
我们接下来分析BUCK电源的两个工作阶段来解释这个问题:
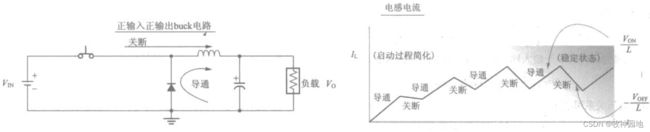
1. BUCK电源处于稳态阶段,电感器电流可以看成两部分电流的叠加:直流电流IAVG和纹波电流IA,直流电流即负载电流(IAVG)部分保持恒定,而且开关电源占空比也保持不变;其实伏秒定律就是在稳态条件下的分析,如下图所示;
2. 如上图所示,电感器最小电流ILmin并非固定不变,理论上可以是任意值,但确定的是不管是在“开关”闭合或关断时电流都不会中断(保持连续);
——电感器的原理决定了流经电感器的电流不可突变。
3. 直流电流在电感器和电容器上不会产生任何作用:电感器(串联)对直流电流来说相当于短路,电容器(并联)对直流电流来说相当于断开,所以对于直流部分的负载电流,电感器和电容器都不会产生任何作用;但对BUCK电源来说直流部分也是能量传输;
——电感器的感值和电容器的容值在理论上并不能限制输出电压和电流的大小,所能影响的是输出电源波动的部分:纹波电流和纹波电压的大小。
4. 所以我们就知道了,虽然都是输入电源Vdc经过电感器L0充电相同的时间Ton,但是它只能决定在Ton时间段的电感器电流的变化(电流变化率一样),而无法决定具体电流的大小(传输能量的大小),其差别在于直流电流的部分。
——负载电流虽然跟电感值没有直接关系,但是与电感器/MOS管额定电流强相关;另外在实际设计中电感值和电容值也与负载电流相关的(具体后续《开关电源设计》章节分析)。
5. 那如果负载电流Io从小突然变大呢?
1,首先负载电流Io突然变大,而此刻BUCK电源的输出能力还未增加;
——通过上面的分析我们知道,电源的负载电流输出能力取决于直流部分,而在稳态时直流部分电流是保持不变的。
2, Io需求增大,这部分增加的电能从输出电容器或储能大电容器提供,但不可避免的是输出电源电压Vo会降低;
3, 输出电源电压Vo降低,则开关电源会自动通过反馈环路增加“开关”占空比,加大电流输出能力,即电感器直流电流IAVG增加;
4, 输出电源电压Vo由于开关电源输出电流能力的提升,恢复到正常电压值,此时IAVG已经增加,占空比恢复到D = Vo/Vin,但此时两者输出电流能力是不同的。以电源启动工作为例,如下图所示。
通过这个问题分析,我相信大家对BUCK电源中的电感器和电容器以及开关管(MOS管)的作用,有了一定的认识。我们再总结一遍:电感器的感性部分(电感值)和电容器的容性部分(电容值)只作用于输出电源的纹波电压和纹波电流。电感器、MOS管以及续流二极管的额定电流决定了输出电流的上限。
——电感器的额定电流,取决于两方面:1,绕组铜线的最大允许电流(表现为温升);2,磁芯饱和所允许最大电流(表现为电感值下降)。(具体请复习:《电感器原理》章节)
3,输出电容器和纹波电压的问题
根据电感公式,我们知道在相同电压下感值L决定了电感器电流的变化率:dI/dt = V/L,即在开关BUCK电源拓扑中电感值影响了纹波电流的大小;但我们在实际工作中并不会直接去测量纹波电流的大小,而是看纹波电压的大小,通过上一节的分析我们已经知道纹波电流并非流入负载端,而是流入输出电容器中,所以纹波电压ΔV = ΔI*Rc。其中∆![]() I 是纹波电流,Rc为输出电容器开关频率对应的ESR(有关电容器ESR的概念,具体请复习:《电容器原理》相关章节)。
I 是纹波电流,Rc为输出电容器开关频率对应的ESR(有关电容器ESR的概念,具体请复习:《电容器原理》相关章节)。
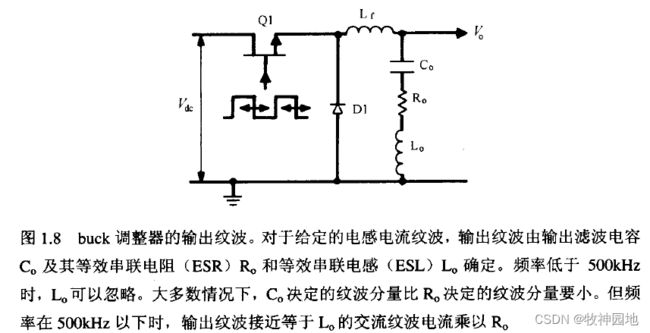
——实际上电容器模型由:电感、电阻和电容组成,但是在较低频率下基本上等效于ESR;具体解释如下图所示。
如上分析仅仅是稳态情况下的纹波电压由输出电容器的ESR和纹波电流决定,如果负载电流突然变化,输出电容器需要实现平滑输出电源电压的作用,所以综合考虑,如下图所示,对输出电容器有如下要求:
1. 输出电容器选择必须满足纹波电压的要求,最大输出纹波峰峰值小于输出电压的1%;纹波电压主要由输出电容器的ESR(Ro)决定;ESR < Vripple_max/(Io*r);
2. 负载突增(动态负载)时,可接受最大电压跌落:ΔVdrop;一般开关电源控制环路大约需要三个开关周期来响应并开始矫正输出,以满足负载突变的需求,在此期间由输出电容器保持电平在Vdrop以上,由于I = C* dV/dt => C> (I*Δt)/ΔV = (I*3T)/ΔVdrop = (I*3)/(ΔVdrop*f) = (3*ΔIo)/( ΔVdrop*f);
3. 负载突减时,可接受最大电压增加: ΔVover;假设负载从最大负载Io突变至0,所有电感能量倾泻到输出电容器中; 1/2*C*(V²x - V²o) = 1/2*L*I²o => C >(L* I²o)/[(Vx+Vo)*(Vx-Vo)] ≈ (L* I²o)/(2*Vo*ΔVover)。