单元格法求解多边形最大内接矩形问题【思路讲解+java实现】

问题描述

给定一个多边形的点集，希望找出多边形内部面积最大的矩形。该问题可能出现在，从一个多边形废料上面切割出一个最大的矩形，该矩形可以重复利用，解决该问题可以节约原材料，降低企业运作成本

问题解决方案

本文主要使用的方法是：将多边形离散化为多个单元格，然后判断哪些单元格处于多边形内部，最后通过遍历内部的单元格来找到面积最大的矩形

多边形网格化

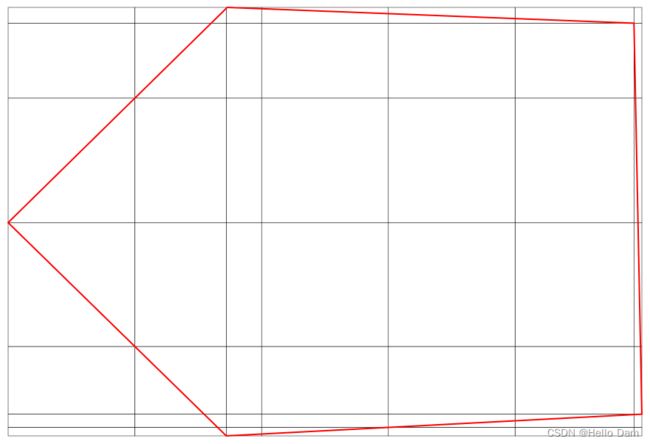
已知每个多边形点集中的每个点的坐标为(y,z)，通过遍历所有点，可以找出minY,maxY,minZ,maxZ，本文使用一个参数segmentNum来决定y轴方向上对多边形多离散的段数，dis=(maxY-minY)/segmentNum为步进长度，每间隔一个步进长度生成一条垂直于于y轴的扫描线，该扫描线会与多边形相交，本文将相交点的z坐标值生成为一条垂直于z轴的扫描线。最终待垂直于y轴或z轴的扫描线都生成完毕之后，会得到如下图所示的网格

segmentNum=5对应的网格

segmentNum=100对应的网格

需要注意的是，为了加快计算速度，可以使用一定的策略来筛选掉部分扫描线，如果两条扫描线之间间隔的距离非常相近，只需要使用其中一条即可，本文使用一个非常简单的策略，例如y=1.2、y=1.3，使用一个map来记录(int)(1.2)=1，因为int(1.3)也等于1，该扫描线会被舍弃

【java代码实现】

/**
 * 构建网络单元
 *
 * @param pointList
 * @return
 */
private Cell[][] constructCells(List<Point> pointList) {
    声明变量
    Cell[][] cells;

    开始构建
    List<Double> yList = new ArrayList<>();
    List<Double> zList = new ArrayList<>();
    Map<Integer, Boolean> yMap = new HashMap<>();
    Map<Integer, Boolean> zMap = new HashMap<>();
    for (Point point : pointList) {
        if (!yMap.containsKey((int) point.getY())) {
            yList.add(point.getY());
            yMap.put((int) point.getY(), true);
        }
        if (!zMap.containsKey((int) point.getZ())) {
            zList.add(point.getZ());
            zMap.put((int) point.getZ(), true);
        }
    }
    根据分段继续添加yList和zList
    double minY = Double.MAX_VALUE;
    double maxY = -Double.MAX_VALUE;
    double minZ = Double.MAX_VALUE;
    double maxZ = -Double.MAX_VALUE;
    for (Point point : pointList) {
        minY = Math.min(minY, point.getY());
        maxY = Math.max(maxY, point.getY());
        minZ = Math.min(minZ, point.getZ());
        maxZ = Math.max(maxZ, point.getZ());
    }
    ///根据分段数来确定y的增量
    double deltaOfY = (maxY - minY) * 1.0 / this.segmentNum;
    double curY = minY + deltaOfY;
    while (curY < maxY) {
        if (yMap.containsKey(curY)) {
            curY += deltaOfY;
            continue;
        }
        boolean isAdd = false;
        // 对于每一根y扫描线，都拿来和多边形的每条边相交一下，来找到z扫描线
        for (int i = 0; i < pointList.size(); i++) {
            int j = (i + 1) % pointList.size();
            //获取边的两个点
            Point point1 = pointList.get(i);
            Point point2 = pointList.get(j);
            double minYOfSide = Math.min(point1.getY(), point2.getY());
            double maxYOfSide = Math.max(point1.getY(), point2.getY());
            if (minYOfSide < curY && curY < maxYOfSide) {
                ///对边构建表达式
                double curZ = this.getZByYAndLineMessage(point1, point2, curY);
                if (curZ == Double.MAX_VALUE) {
                    continue;
                }
                if (!zMap.containsKey((int) curZ)) {
                    zList.add(curZ);
                    zMap.put((int) curZ, true);
                }
                isAdd = true;
            }
        }
        if (isAdd == true) {
            yList.add(curY);
            yMap.put((int) curY, true);
        }
        curY += deltaOfY;
    }
    //对yList、zList升序排序
    Collections.sort(yList);
    Collections.sort(zList);
    cells = new Cell[zList.size() - 1][yList.size() - 1];
    for (int j = 0; j < zList.size() - 1; j++) {
        for (int i = 0; i < yList.size() - 1; i++) {
            Point left_up_point = new Point(0, yList.get(i), zList.get(j));
            Point right_down_point = new Point(0, yList.get(i + 1), zList.get(j + 1));
            cells[j][i] = new Cell(left_up_point, right_down_point);
        }
    }
    return cells;
}

区分每个单元格是在多边形内部还是外部

本文使用的区分方式是，分别判断一个单元格的四个点是否都在多边形内部，判断一个点是否在多边形的内部可以参考文章射线法——判断一个点是否在多边形内部（适用于凸多边形和凹多边形）【关键原理解释+文字伪代码+java代码实现】，只要有一个点不在多边形内部，则该单元格被标记为0，代表其不在多边形内部。如果单元格的四个点都在多边形内部，也不足以说明单元格就真的在多边形内部，下图就是一个例子

因此还需要判断单元格的边和多边形的边是否有相交，如果有相交，则单元格不完全在多边形内部。等所有的单元格都被判断是否完整地处于多边形内部并被标记为1之后，得到下图

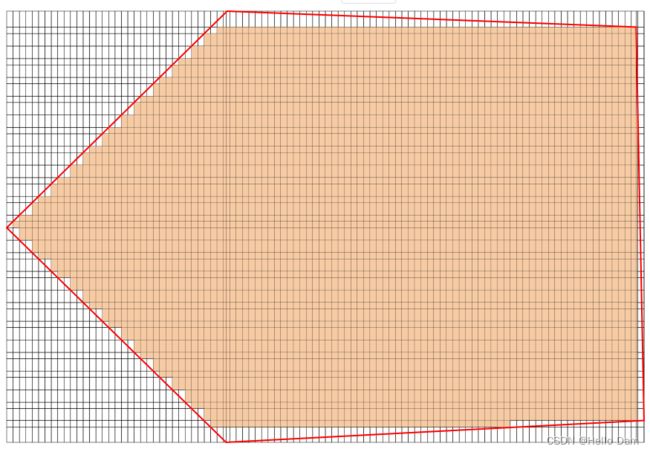
【java实现】

/**
 * 标记网络单元，当一个单元处于多边形内部时，将单元标记为 1，否则标记为 0
 *
 * @param pointList
 * @param cells
 */
private void markCellsLabel(List<Point> pointList, Cell[][] cells) throws Exception {
    long start = System.currentTimeMillis();
    for (int i = 0; i < cells.length; i++) {
        for (int j = 0; j < cells[i].length; j++) {
            cells[i][j].setLabel(this.getCellLabel(pointList, cells[i][j]));
        }
    }
    long end = System.currentTimeMillis();
    this.setCellsLabelTime += end - start;
}

/**
 * 判断单元格是否被纯包含于多边形内，是：返回1；否：返回0
 * 单元格中有一个点不在多边形内，单元格便是不在单元格内
 * type=0:第一次设置label时使用; type=1:reset label时使用;
 *
 * @param pointList
 * @param cell
 */
private int getCellLabel(List<Point> pointList, Cell cell) throws Exception {
    // 存储单元格的四个点
    Point[] pointArr = new Point[4];
    //左上角
    pointArr[0] = new Point(0, cell.getLeft_up_point().getY(), cell.getLeft_up_point().getZ());
    //右上角
    pointArr[1] = new Point(0, cell.getRight_down_point().getY(), cell.getLeft_up_point().getZ());
    //右下角
    pointArr[2] = new Point(0, cell.getRight_down_point().getY(), cell.getRight_down_point().getZ());
    //左下角
    pointArr[3] = new Point(0, cell.getLeft_up_point().getY(), cell.getRight_down_point().getZ());
    
    for (Point point : pointArr) {
        //只要有一个点不在多边形内，单元格被标记为不在多边形内
        if (PolygonUtil.judgeWhetherThePointInPolygon(pointList, point) == false) {
            return 0;
        }
    }

    //就算单元格的所有点都在多边形内部，不代表单元格就在多边形内了
    //再判断一下网络单元的四条边是否和线段有相交，且斜率不能相同，为了避免出现较特殊矩形时，单元的四个点都在多边形内部，但是实际上不在内部的情况出现
    for (int i = 0; i < pointArr.length; i++) {
        int j = (i + 1) % pointArr.length;
        for (int m = 0; m < pointList.size(); m++) {
            int n = (m + 1) % pointList.size();
            if (PolygonUtil.judgeWhetherTwoLineSegmentIsIntersect(pointArr[i], pointArr[j], pointList.get(m), pointList.get(n)) == true &&
                    (this.getKOfLine(pointArr[i], pointArr[j]) != this.getKOfLine(pointList.get(m), pointList.get(n)))) {
                //--if--当单元格的边和多边形有交叉，且不是平行的那种时，单元不在多边形内部
                return 0;
            }
        }
    }
//            System.out.println("单元格在多边形内部");
    return 1;
}

根据已标记单元格寻找最大内接矩形

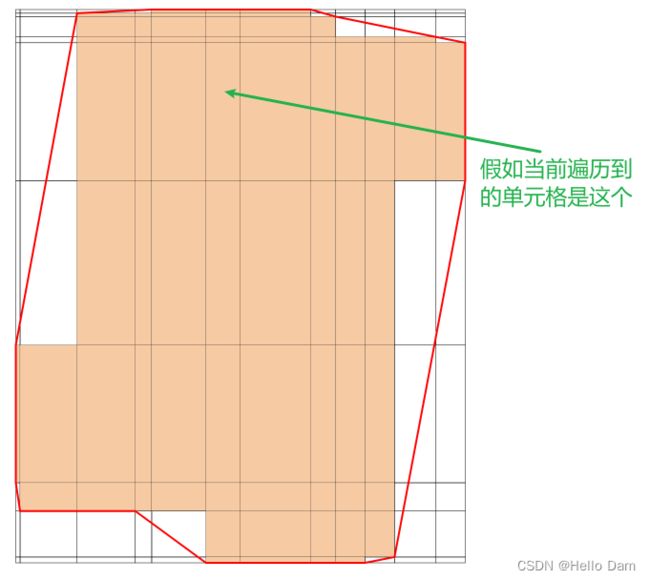
本文寻找最大内接矩形的方式如下：遍历每个单元格，尝试将该单元格开始，然后向右、向下寻找单元格进行组合来找到该单元格最大的矩形。在遍历的途中，不断更新面积最大的矩形，遍历结束之后即可求得结果

当遍历到一个单元格时，从单元格开始，向右遍历每一列，找出每一列的对应的连续高度填充到heightArr中，如下图所示。同理，遍历每一行，找出每一行的连续宽度，填充到widthArr中，同时将每一行最大连续宽度的单元格所在的列索引填充到maxColumnNumArr中

具体操作如下面的代码所示

/*
* 只需要设置一次heightArr，后面需要多少列直接拿就行
* 只需要设置一次widthArr，下一列的格子的所能找到的最大宽度直接为当前格子所能找到的最大宽度-当前格子宽度
*/
double[] widthArr = new double[cells.length - i];
// 存储每一行到达最大宽度时的列数
int[] maxColumnNumArr = new int[cells.length - i];
double[] heightArr = new double[cells[0].length - j];

/// 初始化heightArr
for (int x = j; x < heightArr.length + j; x++) {
   // --for--循环每一列
   double heightOfCurColumn = 0;
   for (int y = i; y < cells.length; y++) {
       // --for--循环每一行
       if (cells[y][x].getLabel() == 1) {
           heightOfCurColumn += cells[y][x].getHeight();
       } else {
           break;
       }
   }
   heightArr[x - j] = heightOfCurColumn;
   if (Math.abs(heightOfCurColumn - 0) < this.precisionError) {
       // 相当于这一列开始，后面的列全是默认为0，因为所形成的矩形需要被最矮的一列限制
       break;
   }
}

/// 初始化 widthArr 和 maxColumnNumArr
for (int m = i; m < widthArr.length + i; m++) {
   // --for--循环每一行
   double widthOfCurRow = 0;
   // 找最大宽度所到达的列数
   int maxColumnNum = j;
   int num = 0;
   for (int k = j; k < cells[0].length; k++) {
       // --for--循环每一列
       if (cells[m][k].getLabel() == 1) {
           widthOfCurRow += cells[m][k].getWidth();
           num++;
       } else {
           break;
       }
   }
   maxColumnNum += num > 0 ? num - 1 : 0;
   // 存储当前行宽度
   widthArr[m - i] = widthOfCurRow;
   maxColumnNumArr[m - i] = maxColumnNum;
}

当遍历到一个单元格时，还需要做如下事情来寻找当前单元格对应的最大矩形，因为文字实在太难描述，我直接贴代码了o(╥﹏╥)o

/// 找到最小的n
// 从widthArr和nArr来看
int minN = Integer.MAX_VALUE;
for (int index = 0; index < maxColumnNumArr.length; index++) {
   if (maxColumnNumArr[index] > 0) {
       minN = Math.min(minN, maxColumnNumArr[index]);
   } else {
       break;
   }
}
if (minN == Integer.MAX_VALUE) {
   // 将minN赋值为j-1，这样下面就无需循环寻找结果了
   minN = j - 1;
}
// 从heightArr来看
int minNOfHeightArr = j;
for (int k = 1; k < heightArr.length; k++) {
   if (heightArr[k] <= heightArr[k - 1]) {
       minNOfHeightArr++;
   } else {
       break;
   }
}
minN = Math.min(minN, minNOfHeightArr);

/// 【寻找最大面积的矩形】
int columnNum = 0;
int recordJ = j;
if (j <= minN) {
   while (j <= minN) {
       if (cells[i][j].getLabel() == 1 && cells[i][j].getMaxArea() > bestArea) {
           for (int m = i; m < widthArr.length + i; m++) {
               // --for--循环每一行
               double widthOfCurRow = widthArr[m - i];
               // 找最大宽度所到达的列数
               int maxColumnNum = maxColumnNumArr[m - i];
               if ((m - i - 1) >= 0 && maxColumnNum == maxColumnNumArr[m - i - 1]) {
                   // --if-- 最大列数和上一个的最大列数一样，可以直接跳过此轮循环，直接进入下一轮
                   continue;
               }
               if (Math.abs(widthOfCurRow - 0) < this.precisionError) {
                   break;
               } else {
                   // 当前行对应的最大宽度
                   double maxWid = widthOfCurRow;
                   // 寻找当前宽度对应的最小高度
                   double maxHei = Integer.MAX_VALUE;
                   boolean isAssign = false;
                   for (int k = columnNum; k < maxColumnNum - recordJ + 1; k++) {
                       maxHei = Math.min(maxHei, heightArr[k]);
                       isAssign = true;
                   }
                   // 更新最优解
                   if (maxWid * maxHei > bestArea && isAssign == true) {
                       bestArea = maxWid * maxHei;
                       bestRectangle = new LoadProductDto(maxWid, maxHei, cells[i][j].getLeft_up_point().getY(), cells[i][j].getLeft_up_point().getZ());
                   }
               }
           }
       }
       // 更新widthArr
       for (int m = i; m < widthArr.length + i; m++) {
           if (widthArr[m - i] > 0) {
               // 每一行的width减去当前列的宽度
               widthArr[m - i] -= cells[m][j].getWidth();
           } else {
               break;
           }
       }
       j++;
       columnNum++;
       break;
   }
   // 上面的j++已经超出minN了，重新回到minN，因为循环的时候，j会++，如果不回到minN，会漏掉一列
   j = minN;
}

代码中注释为【寻找最大面积的矩形】的代码片段主要在做如下的事情，可以结合下面的一系列图片来理解

【从第一列开始寻找矩形】



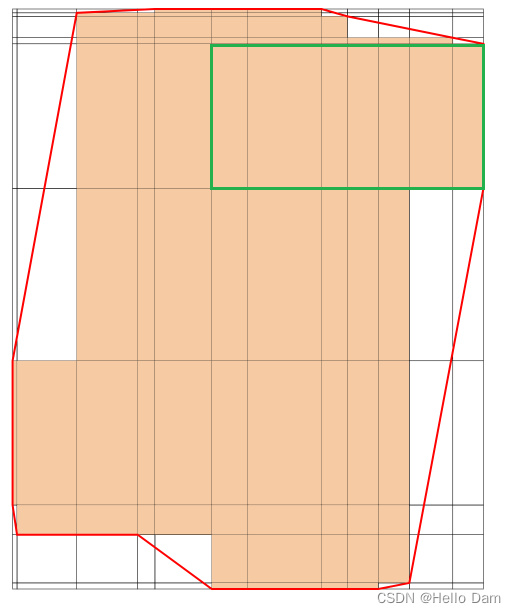
【从第二列开始寻找矩形】

---- 依次类推 ----

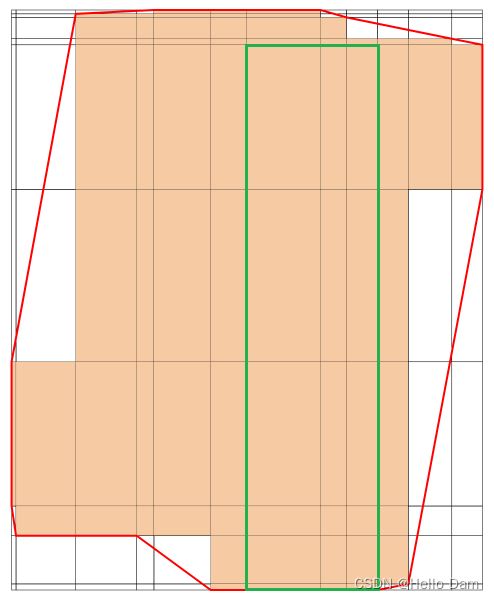
【上面的过程结束之后，下一个遍历的单元格如下图，原因是y已经变成了minN+1】

你们可能会困惑，为啥需要这段代码来限制minN

// 从heightArr来看
int minNOfHeightArr = j;
for (int k = 1; k < heightArr.length; k++) {
   if (heightArr[k] <= heightArr[k - 1]) {
       minNOfHeightArr++;
   } else {
       break;
   }
}
minN = Math.min(minN, minNOfHeightArr);

假如不限制的话，遍历情况如图所示

再直接点说，会找不到如下面类型的结果

剪枝优化

当从网格的左上角遍历到网格的右下角时，能找到的矩形实际上已经非常小了，如果能提前预知一个单元格所能找到的最大矩形面积已经小于当前所找到的最大矩形面积的话，则该单元格无需进行遍历，直接跳过即可

本文使用递推的方法来设置一个单元格所能找到的理想最优矩形面积，代码如下：

/**
* 填充单元格的理想最大面积
*
* @param cells
*/
private void fillCellsMaxArea(Cell[][] cells) {
    填补每个单元格所能找到的理想最大面积(递推)
   /// 初始化网络单元的最后一行和最后一列
   // 初始化最后一行
   for (int i = 0; i < cells[cells.length - 1].length; i++) {
       //对每一列的最后一个单元进行处理
       Cell cell = cells[cells.length - 1][i];
       cell.setMaxArea(cell.getWidth() * cell.getHeight() * cell.getLabel());
   }
   // 初始化最后一列
   for (int i = 0; i < cells.length; i++) {
       //对每一行的最后一个单元进行处理
       Cell cell = cells[i][cells[0].length - 1];
       cell.setMaxArea(cell.getWidth() * cell.getHeight() * cell.getLabel());
   }
   /// 填充其他单元格的理想最大面积
   for (int i = cells.length - 2; i >= 0; i--) {
       for (int j = cells[0].length - 2; j >= 0; j--) {
           Cell cell = cells[i][j];
           //先填充自己的面积
           cell.setMaxArea(cell.getWidth() * cell.getHeight() * cell.getLabel());
           //再添加自己下面的单元格maxArea和右侧的单元格的maxArea
           if (i + 1 < cells.length) {
               cell.setMaxArea(cell.getMaxArea() + cells[i + 1][j].getMaxArea());
           }
           if (j + 1 < cells[0].length) {
               cell.setMaxArea(cell.getMaxArea() + cells[i][j + 1].getMaxArea());
           }
       }
   }
}

当满足单元格的标记为1，且理想最大矩形面积超过当前已经找到的最大矩形面积，才会去根据该单元格去执行上面的【根据已标记单元格寻找最大内接矩形】步骤

// 对每个被标记为1的单元格，将其向右、向下遍历，计算形成的最大矩形
for (int i = 0; i < cells.length; i++) {
    for (int j = 0; j < cells[0].length; j++) {
        if (cells[i][j].getLabel() == 1 && cells[i][j].getMaxArea() > bestArea) {
            // 根据已标记单元格寻找最大内接矩形
        }
    }
}

多角度旋转

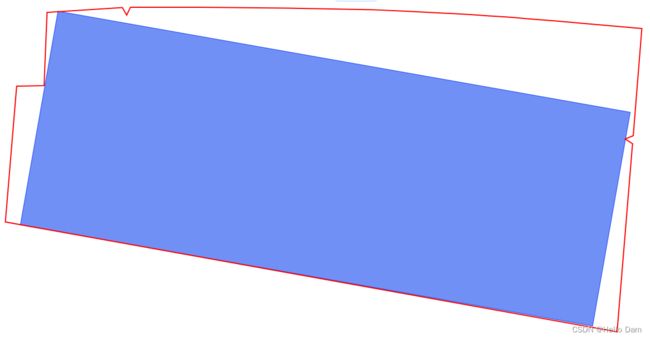
上面的方法结束之后，只能求得一个角度下的最大内接矩形，会导致下图的情况发生

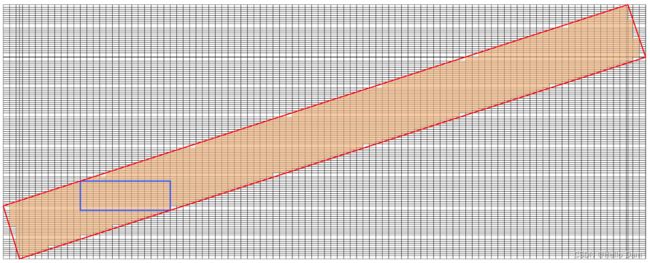
本文通过每旋转5°，求解一个最大内接矩形，最终选择最大的那个矩形作为最终结果，当然，如果想要找到更好的结果，可以不断缩小旋转角度，当然，计算时间也会上涨很多

案例测试

代码实现

package com.ruoyi.algorithm.get_maximumArea_rectangles_in_a_simple_polygon.version.v1;

import com.ruoyi.algorithm.common.entity.Cell;
import com.ruoyi.algorithm.common.entity.GetMaxRectangleInSimplePolygonResult;
import com.ruoyi.algorithm.common.entity.LoadProductDto;
import com.ruoyi.algorithm.common.entity.Point;

import java.util.*;

/**
 * 获取多边形内的最大内接矩形
 */
public class GetMaximumAreaRectangleInASimplePolygonApi {

    /**
     * 对边进行分段处理，增加更多的点
     */
    private int segmentNum = 100;
    /**
     * 是否打印标记矩阵
     */
    private boolean isPrintLabelMatrix = false;
    /**
     * paintType=0：画未补充点的线;paintType=1:画补充点后的线
     */
    private int paintType = 0;
    /**
     * 旋转度数
     */
    private int rotateDegreeDelta = 5;
    /**
     * 精度误差
     */
    private double precisionError = 0.0001;
    /**
     * 标记单元格时间
     */
    private long setCellsLabelTime = 0;
    /**
     * 根据已有解重置单元格标记的时间
     */
    private long resetCellsLabelTime = 0;
    /**
     * 给定单元格，寻找解的时间
     */
    private long searchSolutionTime = 0;

    /**
     * 且多边形的最大内接矩形
     *
     * @param pointList         顺时针或逆时针将点集传进来
     * @param bestRectangleList 可能有多个相等的内接矩形，都存储下来
     */
    public GetMaxRectangleInSimplePolygonResult solve(List<Point> pointList, List<LoadProductDto> bestRectangleList) throws Exception {
        System.out.println();

        long start = System.currentTimeMillis();

        声明变量
        List<Point> solution = new ArrayList<>();
        GetMaxRectangleInSimplePolygonResult getMaxRectangleInSimplePolygonResult = new GetMaxRectangleInSimplePolygonResult();

        存储到结果的数据
        List<Double> yList = new ArrayList<>();
        List<Double> zList = new ArrayList<>();
        double minY = Double.MAX_VALUE;
        double maxY = -Double.MAX_VALUE;
        double minZ = Double.MAX_VALUE;
        double maxZ = -Double.MAX_VALUE;
        Cell[][] cells = null;
        for (Point point : pointList) {
            minY = Math.min(minY, point.getY());
            maxY = Math.max(maxY, point.getY());
            minZ = Math.min(minZ, point.getZ());
            maxZ = Math.max(maxZ, point.getZ());
        }

        找最大矩形
        ///声明变量
        //记录最大矩形的面积
        double bestArea = 0;
        //记录最佳旋转角度
        int bestRotateDegree = 0;
        LoadProductDto bestRectangle = null;
        List<Point> bestSolution = new ArrayList<>();
        //记录当前所遍历到的角度
        int rotateDegree = 0;
        int endRotateDegree = 360;
        while (rotateDegree <= endRotateDegree) {
//            System.out.println("当前角度："+rotateDegree);
            //每旋转rotateDegreeDelta，求一次结果，取中间的最优解
            LoadProductDto curRectangle = this.solveWithAppointRotateDegree(Point.cloneList(pointList), rotateDegree, solution);
            if (curRectangle == null) {
                rotateDegree += this.rotateDegreeDelta;
                continue;
            }
            //更新结果
            double curArea = curRectangle.getWidth() * curRectangle.getHeight();
            if ((bestRectangle == null) || (curArea > bestArea)) {
                System.out.println("找到矩形1-------------------------");
                //找curRectangle的4个角点
                List<Point> curSolution = new ArrayList<>();
                Point leftUpPoint = new Point(0, curRectangle.getY(), curRectangle.getZ());
                Point rightUpPoint = new Point(0, curRectangle.getY() + curRectangle.getWidth(), curRectangle.getZ());
                Point rightDownPoint = new Point(0, curRectangle.getY() + curRectangle.getWidth(), curRectangle.getZ() + curRectangle.getHeight());
                Point leftDownPoint = new Point(0, curRectangle.getY(), curRectangle.getZ() + curRectangle.getHeight());
                Collections.addAll(curSolution, leftDownPoint, rightDownPoint, rightUpPoint, leftUpPoint);
                //对结果进行反旋转
                for (Point point : curSolution) {
                    double[] arr = this.rotate(point.getY(), point.getZ(), 0, 0, -rotateDegree);
                    point.setY(arr[0]);
                    point.setZ(arr[1]);
                }
                //替换结果
                bestArea = curArea;
                bestRectangle = curRectangle;
                bestSolution.clear();
                bestSolution.addAll(curSolution);
                bestRotateDegree = rotateDegree;
                bestRectangle.setBestRotateDegree(bestRotateDegree);
            }
            rotateDegree += this.rotateDegreeDelta;
        }
        if (bestRectangle != null) {
            //找到解，对解进行存储
            solution = Point.cloneList(bestSolution);
            System.out.println("找到矩形2-------------------------");
            System.out.println("最优旋转角度:" + bestRotateDegree);
            System.out.println("bestSolution:" + bestSolution);
            bestRectangleList.add(bestRectangle);
            ///存储最优解，需要将网格那些也保存下来
            if (this.paintType == 1) {
                minY = Double.MAX_VALUE;
                maxY = -Double.MAX_VALUE;
                minZ = Double.MAX_VALUE;
                maxZ = -Double.MAX_VALUE;
                // 将零件点旋转一下
                for (Point point : pointList) {
                    double[] arr = this.rotate(point.getY(), point.getZ(), 0, 0, bestRotateDegree);
                    point.setY(arr[0]);
                    point.setZ(arr[1]);
                    minY = Math.min(minY, point.getY());
                    maxY = Math.max(maxY, point.getY());
                    minZ = Math.min(minZ, point.getZ());
                    maxZ = Math.max(maxZ, point.getZ());
                }
                // 将结旋转一下
                for (Point point : solution) {
                    double[] arr = this.rotate(point.getY(), point.getZ(), 0, 0, bestRotateDegree);
                    point.setY(arr[0]);
                    point.setZ(arr[1]);
                }
                //构建网络单元
                cells = this.constructCells(pointList);
                //标记单元格，所有被全包含于多边形的单元格被标记为1
                this.markCellsLabel(pointList, cells);
            }
        }
        getMaxRectangleInSimplePolygonResult.setSolution(solution);
        getMaxRectangleInSimplePolygonResult.setPointList(pointList);
        getMaxRectangleInSimplePolygonResult.setBestRectangleList(bestRectangleList);
        getMaxRectangleInSimplePolygonResult.setYList(yList);
        getMaxRectangleInSimplePolygonResult.setZList(zList);
        getMaxRectangleInSimplePolygonResult.setWidth(maxY - minY);
        getMaxRectangleInSimplePolygonResult.setHeight(maxZ - minZ);
        getMaxRectangleInSimplePolygonResult.setMinY(minY);
        getMaxRectangleInSimplePolygonResult.setMinZ(minZ);
        getMaxRectangleInSimplePolygonResult.setCells(cells);
        long end = System.currentTimeMillis();
        double calculateTime = (end - start) * 1.0 / 1000;
        getMaxRectangleInSimplePolygonResult.setCalculateTime(calculateTime);

        System.out.println("结果输出--------------------------------------------------");
        System.out.println("计算时间：" + calculateTime + "s");
        System.out.println("标记网络单元总标记时间：" + this.setCellsLabelTime * 1.0 / 1000 + "s");
        System.out.println("重置网络单元总标记时间：" + this.resetCellsLabelTime * 1.0 / 1000 + "s");
        System.out.println("给定网络搜索解时间：" + this.searchSolutionTime * 1.0 / 1000 + "s");

        return getMaxRectangleInSimplePolygonResult;
    }

    /**
     * 指定旋转角度，求当前旋转角度的最大矩形
     *
     * @param pointList
     * @param rotateDegree
     * @return
     */
    private LoadProductDto solveWithAppointRotateDegree(List<Point> pointList, int rotateDegree, List<Point> solution) throws Exception {

         数据处理
        // 将点旋转一下
        for (Point point : pointList) {
            double[] arr = this.rotate(point.getY(), point.getZ(), 0, 0, rotateDegree);
            point.setY(arr[0]);
            point.setZ(arr[1]);
        }

         声明变量
        double bestArea = 0;
        LoadProductDto bestRectangle = null;

        // 构建单元格
        Cell[][] cells = this.constructCells(pointList);
        // 标记单元格，所有被全包含于多边形的单元格被标记为1
        this.markCellsLabel(pointList, cells);
        if (this.isPrintLabelMatrix == true) {
            System.out.println("输出真实标记矩阵，在多边形内的单元被标记为1");
            for (int i = 0; i < cells.length; i++) {
                for (int j = 0; j < cells[i].length; j++) {
                    System.out.printf(String.valueOf(cells[i][j].getLabel()) + "\t");
                }
                System.out.println();
            }
        }
        // 填充单元格的最大面积(搜索到右下角的单元格时，如果知道所能找到的矩形一定不可能大于已经搜索到的矩形时，直接停止该单元格的搜索)
        this.fillCellsMaxArea(cells);
        // 对每个被标记为1的单元格，将其向右、向下遍历，计算形成的最大矩形
        for (int i = 0; i < cells.length; i++) {
            for (int j = 0; j < cells[0].length; j++) {
                if (cells[i][j].getLabel() == 1 && cells[i][j].getMaxArea() > bestArea) {
                    /*
                     * 只需要设置一次heightArr，后面需要多少列直接拿就行
                     * 只需要设置一次widthArr，下一列的格子的所能找到的最大宽度直接为当前格子所能找到的最大宽度-当前格子宽度
                     */
                    long searchSolutionTimeStart = System.currentTimeMillis();
                    double[] widthArr = new double[cells.length - i];
                    // 存储每一行到达最大宽度时的列数
                    int[] maxColumnNumArr = new int[cells.length - i];
                    double[] heightArr = new double[cells[0].length - j];

                    /// 初始化heightArr
                    for (int x = j; x < heightArr.length + j; x++) {
                        // --for--循环每一列
                        double heightOfCurColumn = 0;
                        for (int y = i; y < cells.length; y++) {
                            // --for--循环每一行
                            if (cells[y][x].getLabel() == 1) {
                                heightOfCurColumn += cells[y][x].getHeight();
                            } else {
                                break;
                            }
                        }
                        heightArr[x - j] = heightOfCurColumn;
                        if (Math.abs(heightOfCurColumn - 0) < this.precisionError) {
                            // 相当于这一列开始，后面的列全是默认为0，因为所形成的矩形需要被最矮的一列限制
                            break;
                        }
                    }

                    /// 初始化 widthArr 和 maxColumnNumArr
                    for (int m = i; m < widthArr.length + i; m++) {
                        // --for--循环每一行
                        double widthOfCurRow = 0;
                        // 找最大宽度所到达的列数
                        int maxColumnNum = j;
                        int num = 0;
                        for (int k = j; k < cells[0].length; k++) {
                            // --for--循环每一列
                            if (cells[m][k].getLabel() == 1) {
                                widthOfCurRow += cells[m][k].getWidth();
                                num++;
                            } else {
                                break;
                            }
                        }
                        maxColumnNum += num > 0 ? num - 1 : 0;
                        // 存储当前行宽度
                        widthArr[m - i] = widthOfCurRow;
                        maxColumnNumArr[m - i] = maxColumnNum;
                    }

                    /// 找到最小的n
                    // 从widthArr和nArr来看
                    int minN = Integer.MAX_VALUE;
                    for (int index = 0; index < maxColumnNumArr.length; index++) {
                        if (maxColumnNumArr[index] > 0) {
                            minN = Math.min(minN, maxColumnNumArr[index]);
                        } else {
                            break;
                        }
                    }
                    if (minN == Integer.MAX_VALUE) {
                        // 将minN赋值为j-1，这样下面就无需循环寻找结果了
                        minN = j - 1;
                    }
                    // 从heightArr来看
                    int minNOfHeightArr = j;
                    for (int k = 1; k < heightArr.length; k++) {
                        if (heightArr[k] <= heightArr[k - 1]) {
                            minNOfHeightArr++;
                        } else {
                            break;
                        }
                    }
                    minN = Math.min(minN, minNOfHeightArr);

                    /// 寻找最大面积的矩形
                    int columnNum = 0;
                    int recordJ = j;
                    if (j <= minN) {
                        while (j <= minN) {
                            if (cells[i][j].getLabel() == 1 && cells[i][j].getMaxArea() > bestArea) {
                                for (int m = i; m < widthArr.length + i; m++) {
                                    // --for--循环每一行
                                    double widthOfCurRow = widthArr[m - i];
                                    // 找最大宽度所到达的列数
                                    int maxColumnNum = maxColumnNumArr[m - i];
                                    if ((m - i - 1) >= 0 && maxColumnNum == maxColumnNumArr[m - i - 1]) {
                                        // --if-- 最大列数和上一个的最大列数一样，可以直接跳过此轮循环，直接进入下一轮
                                        continue;
                                    }
                                    if (Math.abs(widthOfCurRow - 0) < this.precisionError) {
                                        break;
                                    } else {
                                        // 当前行对应的最大宽度
                                        double maxWid = widthOfCurRow;
                                        // 寻找当前宽度对应的最小高度
                                        double maxHei = Integer.MAX_VALUE;
                                        boolean isAssign = false;
                                        for (int k = columnNum; k < maxColumnNum - recordJ + 1; k++) {
                                            maxHei = Math.min(maxHei, heightArr[k]);
                                            isAssign = true;
                                        }
                                        // 更新最优解
                                        if (maxWid * maxHei > bestArea && isAssign == true) {
                                            bestArea = maxWid * maxHei;
                                            bestRectangle = new LoadProductDto(maxWid, maxHei, cells[i][j].getLeft_up_point().getY(), cells[i][j].getLeft_up_point().getZ());
                                        }
                                    }
                                }
                            }
                            // 更新widthArr
                            for (int m = i; m < widthArr.length + i; m++) {
                                if (widthArr[m - i] > 0) {
                                    // 每一行的width减去当前列的宽度
                                    widthArr[m - i] -= cells[m][j].getWidth();
                                } else {
                                    break;
                                }
                            }
                            j++;
                            columnNum++;
                            break;
                        }
                        // 上面的j++已经超出minN了，重新回到minN，因为循环的时候，j会++，如果不回到minN，会漏掉一列
                        j = minN;
                    }
                    long searchSolutionTimeEnd = System.currentTimeMillis();
                    this.searchSolutionTime += searchSolutionTimeEnd - searchSolutionTimeStart;
                }
            }
        }

        return bestRectangle;
    }

    /**
     * 构建网络单元
     *
     * @param pointList
     * @return
     */
    private Cell[][] constructCells(List<Point> pointList) {
        声明变量
        Cell[][] cells;

        开始构建
        List<Double> yList = new ArrayList<>();
        List<Double> zList = new ArrayList<>();
        Map<Integer, Boolean> yMap = new HashMap<>();
        Map<Integer, Boolean> zMap = new HashMap<>();
        for (Point point : pointList) {
            if (!yMap.containsKey((int) point.getY())) {
                yList.add(point.getY());
                yMap.put((int) point.getY(), true);
            }
            if (!zMap.containsKey((int) point.getZ())) {
                zList.add(point.getZ());
                zMap.put((int) point.getZ(), true);
            }
        }
        根据分段继续添加yList和zList
        double minY = Double.MAX_VALUE;
        double maxY = -Double.MAX_VALUE;
        double minZ = Double.MAX_VALUE;
        double maxZ = -Double.MAX_VALUE;
        for (Point point : pointList) {
            minY = Math.min(minY, point.getY());
            maxY = Math.max(maxY, point.getY());
            minZ = Math.min(minZ, point.getZ());
            maxZ = Math.max(maxZ, point.getZ());
        }
        ///根据分段数来确定y的增量
        double deltaOfY = (maxY - minY) * 1.0 / this.segmentNum;
        double curY = minY + deltaOfY;
        while (curY < maxY) {
            if (yMap.containsKey(curY)) {
                curY += deltaOfY;
                continue;
            }
            boolean isAdd = false;
            // 对于每一根y扫描线，都拿来和多边形的每条边相交一下，来找到z扫描线
            for (int i = 0; i < pointList.size(); i++) {
                int j = (i + 1) % pointList.size();
                //获取边的两个点
                Point point1 = pointList.get(i);
                Point point2 = pointList.get(j);
                double minYOfSide = Math.min(point1.getY(), point2.getY());
                double maxYOfSide = Math.max(point1.getY(), point2.getY());
                if (minYOfSide < curY && curY < maxYOfSide) {
                    ///对边构建表达式
                    double curZ = this.getZByYAndLineMessage(point1, point2, curY);
                    if (curZ == Double.MAX_VALUE) {
                        continue;
                    }
                    if (!zMap.containsKey((int) curZ)) {
                        zList.add(curZ);
                        zMap.put((int) curZ, true);
                    }
                    isAdd = true;
                }
            }
            if (isAdd == true) {
                yList.add(curY);
                yMap.put((int) curY, true);
            }
            curY += deltaOfY;
        }
        //对yList、zList升序排序
        Collections.sort(yList);
        Collections.sort(zList);
        cells = new Cell[zList.size() - 1][yList.size() - 1];
        for (int j = 0; j < zList.size() - 1; j++) {
            for (int i = 0; i < yList.size() - 1; i++) {
                Point left_up_point = new Point(0, yList.get(i), zList.get(j));
                Point right_down_point = new Point(0, yList.get(i + 1), zList.get(j + 1));
                cells[j][i] = new Cell(left_up_point, right_down_point);
            }
        }
        return cells;
    }

    /**
     * 标记网络单元，当一个单元处于多边形内部时，将单元标记为1，否则标记为0
     *
     * @param pointList
     * @param cells
     */
    private void markCellsLabel(List<Point> pointList, Cell[][] cells) throws Exception {
        long start = System.currentTimeMillis();
        for (int i = 0; i < cells.length; i++) {
            for (int j = 0; j < cells[i].length; j++) {
                cells[i][j].setLabel(this.getCellLabel(pointList, cells[i][j]));
            }
        }
        long end = System.currentTimeMillis();
        this.setCellsLabelTime += end - start;
    }

    /**
     * 判断单元格是否被纯包含于多边形内，是：返回1；否：返回0
     * 单元格中有一个点不在多边形内，单元格便是不在单元格内
     * type=0:第一次设置label时使用; type=1:reset label时使用;
     *
     * @param pointList
     * @param cell
     */
    private int getCellLabel(List<Point> pointList, Cell cell) throws Exception {
        // 存储单元格的四个点
        Point[] pointArr = new Point[4];
        //左上角
        pointArr[0] = new Point(0, cell.getLeft_up_point().getY(), cell.getLeft_up_point().getZ());
        //右上角
        pointArr[1] = new Point(0, cell.getRight_down_point().getY(), cell.getLeft_up_point().getZ());
        //右下角
        pointArr[2] = new Point(0, cell.getRight_down_point().getY(), cell.getRight_down_point().getZ());
        //左下角
        pointArr[3] = new Point(0, cell.getLeft_up_point().getY(), cell.getRight_down_point().getZ());

        for (Point point : pointArr) {
            //只要有一个点不在多边形内，单元格被标记为不在多边形内
            if (PolygonUtil.judgeWhetherThePointInPolygon(pointList, point) == false) {
                return 0;
            }
        }

        //就算单元格的所有点都在多边形内部，不代表单元格就在多边形内了
        //再判断一下网络单元的四条边是否和线段有相交，且斜率不能相同，为了避免出现较特殊矩形时，单元的四个点都在多边形内部，但是实际上不在内部的情况出现
        for (int i = 0; i < pointArr.length; i++) {
            int j = (i + 1) % pointArr.length;
            for (int m = 0; m < pointList.size(); m++) {
                int n = (m + 1) % pointList.size();
                if (PolygonUtil.judgeWhetherTwoLineSegmentIsIntersect(pointArr[i], pointArr[j], pointList.get(m), pointList.get(n)) == true &&
                        (this.getKOfLine(pointArr[i], pointArr[j]) != this.getKOfLine(pointList.get(m), pointList.get(n)))) {
                    //--if--当单元格的边和多边形有交叉，且不是平行的那种时，单元不在多边形内部
                    return 0;
                }
            }
        }
//            System.out.println("单元格在多边形内部");
        return 1;
    }

    /**
     * 填充单元格的理想最大面积
     *
     * @param cells
     */
    private void fillCellsMaxArea(Cell[][] cells) {
         填补每个单元格所能找到的理想最大面积(递推)
        /// 初始化网络单元的最后一行和最后一列
        // 初始化最后一行
        for (int i = 0; i < cells[cells.length - 1].length; i++) {
            //对每一列的最后一个单元进行处理
            Cell cell = cells[cells.length - 1][i];
            cell.setMaxArea(cell.getWidth() * cell.getHeight() * cell.getLabel());
        }
        // 初始化最后一列
        for (int i = 0; i < cells.length; i++) {
            //对每一行的最后一个单元进行处理
            Cell cell = cells[i][cells[0].length - 1];
            cell.setMaxArea(cell.getWidth() * cell.getHeight() * cell.getLabel());
        }
        /// 填充其他单元格的理想最大面积
        for (int i = cells.length - 2; i >= 0; i--) {
            for (int j = cells[0].length - 2; j >= 0; j--) {
                Cell cell = cells[i][j];
                //先填充自己的面积
                cell.setMaxArea(cell.getWidth() * cell.getHeight() * cell.getLabel());
                //再添加自己下面的单元格maxArea和右侧的单元格的maxArea
                if (i + 1 < cells.length) {
                    cell.setMaxArea(cell.getMaxArea() + cells[i + 1][j].getMaxArea());
                }
                if (j + 1 < cells[0].length) {
                    cell.setMaxArea(cell.getMaxArea() + cells[i][j + 1].getMaxArea());
                }
            }
        }
    }


    /**
     * 求一条直线的斜率
     *
     * @param p1
     * @param p2
     * @return
     */
    private double getKOfLine(Point p1, Point p2) {
        return MathUtil.getKOfLine(p1.getY(), p1.getZ(), p2.getY(), p2.getZ());
    }

    /**
     * 平面上一点x1,y1,绕平面上另一点x2,y2顺时针旋转rotateDegree角度，求旋转后的x1,y1对应的坐标x，y
     *
     * @param x1
     * @param y1
     * @param x2
     * @param y2
     * @param rotateDegree
     * @return arr[0]:x;arr[1]:y
     */
    private double[] rotate(double x1, double y1, double x2, double y2, int rotateDegree) {
        double[] arr = new double[2];
        //根据角度求弧度
        double radian = (rotateDegree * 1.0 / 180) * Math.PI;
        //旋转
        arr[0] = (x1 - x2) * Math.cos(radian) - (y1 - y2) * Math.sin(radian) + x2;
        arr[1] = (y1 - y2) * Math.cos(radian) + (x1 - x2) * Math.sin(radian) + y2;
        return arr;
    }

    /**
     * 传入一条线段，然后根据已知的y来求线段上的z
     *
     * @param p1
     * @param p2
     * @param y
     * @return
     */
    private double getZByYAndLineMessage(Point p1, Point p2, double y) {
        double k = this.getKOfLine(p1, p2);
        if (Math.abs(k - Double.MAX_VALUE) < this.precisionError) {
            return Double.MAX_VALUE;
        } else if (Math.abs(k - 0) < this.precisionError) {
            return p1.getZ();
        } else {
            //截距
            double b = p2.getZ() - k * p2.getY();
            return k * y + b;
        }
    }

    public GetMaximumAreaRectangleInASimplePolygonApi() {
    }
}

代码中使用的一些工具类麻烦查看文章射线法——判断一个点是否在多边形内部（适用于凸多边形和凹多边形）【关键原理解释+文字伪代码+java代码实现】

说明

本文的算法算是比较粗暴的求解算法，加上本人代码能力不够强，编码时间短，部分地方的处理还有待提高，可能导致部分数据计算时间较长，假如读者们有什么更好的建议也希望可以不吝赐教。如果你们觉得有帮助，也希望可以点个赞