遗传算法整理

1、基本概念
使用群体搜索技术，将种群代表一组问题解，通过对当前种群施加选择、交叉和变异等一系列遗传操作来产生新一代种群，并逐步使种群进化到包含近似最优解的状态。

2、遗传算法流程

3、标准遗传算法
标准遗传算法又称为经典遗传算法，它的优化变量由二进制编码来描述，多个优化变量的二进制编码串接在一起组成染色体，这种编码既适用于变异操作，又适用于交叉操作。在创建初始群体时，代表个体的二进制串是在一定字长的限制下随机产生的。

例 2.1 用标准遗传算法求函数 f(x) = x + 10sin(5x) + 7cos(4x) 的最大值，其中 x 的取值范围为[0，10]。

1）创建初始群体

NP = 50; %群体规模 一般取10~200
L = 20; %二进制位串长度
Pc = 0.8; %交叉概率 0.25~1.00
Pm = 0.1; %变异概率 0.001~0.1
G = 100; %最大遗传代数 100~1000
Xs = 10; % x取值上界
Xx = 0; % x取值下界
f = round(rand(50,20)); %随机生成50x20的矩阵，每个元素均为0/1，每一行表示一个个体

2）计算适应度值
常见的适应度函数构造方法主要有：目标函数映射成适应度函数、基于序的适应度函数等。
将每一个二进制个体转化为十进制，并将数值调整到定义域内，带入目标函数计算适应度值

%适应度函数
function result = func1(x)
fit = x+10*sin(5*x)+7*cos(4*x);
result = fit;
end

 for i = 1:NP %二进制换十进制
        U = f(i,:);
        m = 0;
        for j = 1:L
            m = U(j)*2^(j-1)+m;
        end
        x(i) = Xx+m*(Xs-Xx)/(2^L-1);
        Fit(i) = func1(x(i)); 
    end
    maxFit = max(Fit);
    minFit = min(Fit);
    rr = find(Fit==maxFit); %适应度最大元素的下标
    fBest = f(rr(1,1),:);%二进制初始群体中适应度最大个体
    xBest = x(rr(1,1));%缩小至0-10中该个体所对应的十进制
    %因为适度最大可能对应多个个体，但是只选其中一个作为最优，所以r（1，1）
    Fit = (Fit - minFit)/(maxFit-minFit);%归一化适应度值
    %选择时用“轮盘赌”方法，需要与0-1的指针的进行对比，所以将适应度值进行归一，缩小至0-1

3）选择操作
“轮盘赌”选择法
原理参考：https://blog.csdn.net/qq_33649817/article/details/86582420

sum_Fit = sum(Fit);
    fitvalue = Fit./sum_Fit;
    fitvalue = cumsum(fitvalue); %累积和  1x50
    ms = sort(rand(NP,1));%按升序对元素进行排序 50x1
    fiti = 1;
    newi = 1;%选择指针
    while newi <= NP
        if (ms(newi))<fitvalue(fiti)
            nf(newi,:) = f(fiti,:);
            newi = newi+1;
        else
            fiti = fiti+1;
        end
    end

整理的过程中考虑了一下会不会存在fitvalue先遍历完的情况，感觉是不会存在，因为最后一个fitvalue为1，rand随机生成的值是小于1的。

4）交叉操作
交叉算子作用在按交叉概率选中的两个染色体上，随机选中交叉位置，将两个染色体上对应于这些位置上的二进制数值交换，生成两个新的个体。

 % 基于概率的交叉操作
    for i = 1:2:NP %相邻两个为一对交叉染色体组
        p = rand;
        if p<Pc % Pc 交叉率0.8 选择要进行交叉操作的两个染色体
            q = round(rand(1,L)); %1x20 元素均为0/1 选择进行交叉操作的基因位置，等于1的位置进行二进制数值交换
            for j = 1:L 
                if q(j) == 1
                    temp = nf(i+1,j) ;
                    nf(i+1,j) = nf(i,j);
                    nf(i,j) = temp;
                end
            end
        end
    end

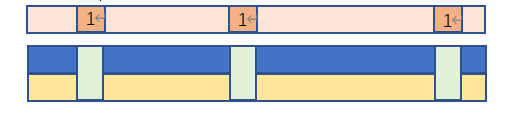
5）变异操作
变异算子作用在按变异概率随机选中的个体上，一般是随机选定变异位，将该位的二进制值取反，生成一个新的个体。

 %基于概率的变异操作
    i = 1;
    while i<= round(NP*Pm) %染色体变异的个数
        h = randi(NP); %随机选取一个需要变异的染色体
        for j = 1:round(L*Pm) % 基因变异的个数
            g = randi(L); %随机选取一个需要变异的基因
            nf(h,g) = ~nf(h,g); % ~非，取反
        end
        i = i+1;
    end

4、君主方案
对群体根据适应度值高低进行排序的基础上，用最优个体与其他偶数位的所有个体进行交叉，每次交叉产生两个新的个体，用于选择和交叉操作。

% 采用君主方案进行选择交叉操作
    Emper = Sortf(:,1);%问题求最小值，按照升序排列适应度值，第一个为最优个体
    NoPoint = round(D*Pc); %每次交叉点的个数
    PoPoint = randi(D,NoPoint,NP/2); %交叉基因的位置 NoPointxNP/2
    nf = Sortf;
    for i = 1:NP/2
        nf(:,2*i-1) = Emper; %将奇数列均变为Emper
       % nf(:,2*i) = Sortf(:,2*i);
        for k = 1:NoPoint
            nf(PoPoint(k,i),2*i-1) = nf(PoPoint(k,i),2*i);%相邻两列进行交叉变换产生两个新个体
            nf(PoPoint(k,i),2*i) = Emper(PoPoint(k,i));
        end
    end

假设NoPoint=8,NP/2=10，得到每一组染色体应该交叉的基因位置


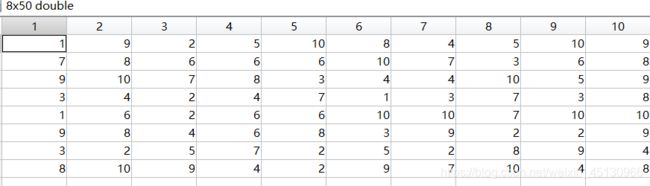
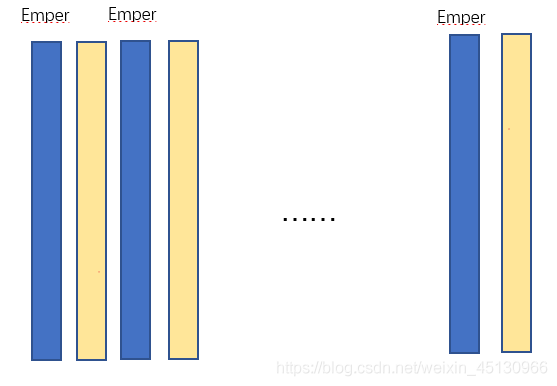
交叉变异之后，计算子群体的适应度值，然后将子群体与父群体合并，并且根据适应度值进行排序，取前NP个个体为新群体，进行下一次遗传操作。

%子种群按适应度升序排列
    for np = 1:NP
        NMSLL(np) = func2(nf(:,np));
    end
    [NSortMSLL,Index] = sort(NMSLL);
    NSortf = nf(:,Index);
% 产生新种群 将两个种群合并，并排序，选取前NP个
    f1 = [Sortf,NSortf];
    MSLL1 = [SortMSLL,NSortMSLL];
    [SortMSLL1,Index] = sort(MSLL1);
    Sortf1 = f1(:,Index);
    SortMSLL = SortMSLL1(1:NP);
    Sortf = Sortf1(:,1:NP);
    trace(gen) = SortMSLL(1); %历代最优适应度值