最长上升子序列优化（贪心+二分）（超级详细的讲解）

一、回顾

1、问题描述

2、动规代码弊端

我们之前的动规代码的时间复杂度是$O(n^2)$。如果大家还不知道动态规划的逻辑的话，建议大家先去看一下动态规划的解决思路：动态规划解决最长上升子序列

虽然动态规划的思路已经比DFS的做法快了很多，但是当数据量增大以后，$O(n^2)$的时间复杂度还是会超时的，那么我们能否进一步优化呢？

我们接着往下看。

二、优化

1、算法优化

我们先看下面的例子：

上述红色部分是最长上升子序列。

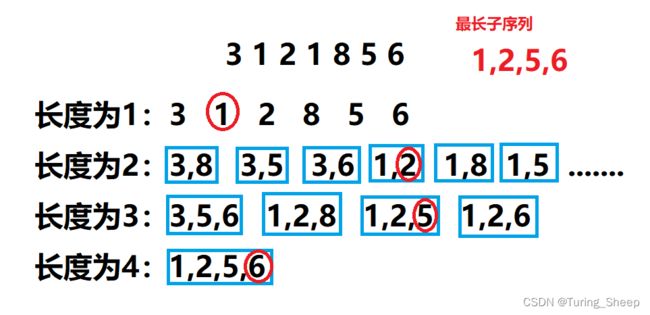
我们发现：

第一个元素$1$，就是长度为$1$的所有子序列中最小的最后一个元素。

第二个元素$2$，就是长度为$2$的所有子序列中最小的最后一个元素。

第三个元素$5$，就是长度为$3$的所有子序列中最小的最后一个元素。

第四个元素$6$，就是长度为$4$的所有子序列中最小的最后一个元素。

我们现在想一想，这是为什么呢？

我们长度为$(len+1)$的子序列，是在长度为$(len)$的子序列的基础上发展而来的。

而我的子序列能否边长，其实是取决于子序列的最后一位。

最后一位越小，我的子序列越容易变长。

---

我们可以简单证明一下：

假设我们的最长上升子序列的长度是$len$，而该序列中的前$k$个元素组成的子序列中（$a[k]$是这个子序列的最后一位），$a[k]$不是最小的那一位，即存在一个以$j$为结尾的长度为$k$的子序列（两个子序列只有最后一位不同），并且$j<a[k]$，同时这个序列并不是最终答案的一部分。

由于答案是严格单调增的序列，那么必定存在$a[k-1]<a[k]<a[k+1]$，又因为两个长度为$k$的子序列只有最后一位不同，所以必定满足$j>a[k-1]$。

那么此时必定存在以下等式：

$$a[k-1]<j<a[k]<a[k+1]$$

也就是说，我们可以将我们假想的$j$插入到答案中，使得其长度变成$(len+1)$。而我们假设最大就是$len$，可是我们却推导出了一个比$len$更大的上升子序列。所以产生了矛盾，假设不成立。

---

因此，我们得出结论：

最长上升子序列中的某一位$a[i]$，必定是长度为$i$的子序列的最后一位中，最小的一个。

所以，我们维护这样一个数组$q[i]$。

这个数组记录的是子序列长度为$i$的序列中，最后一位中最小的最后一位。如果我们碰到了一个$a[i]$。

同时，这个$a[i]$满足$q[k]<a[i]<q[k+1]$。

此时，就说明这个$a[i]$是可以接在长度为$k$的子序列后面，从而让这个序列的长度变成$(k+1)$。

而此时的$a[i]<q[k+1]$，说明长度为$k+1$的子序列中，又出现了一个比原最小值更小的$a[i]$。

所以我们此时更新一下：$q[k+1]=a[i]$。

于是目前的问题，就是我们遍历到一个数值的时候，我们要立刻找到$q[k]$和$q[k+1]$:

使得$q[k]<a[i]<q[k+1]$

而经过我们刚才的分析，其实遍历过后，这个$q[N]$数组就是我们的最长的上升子序列的具体内容，所以这个序列必定是升序的。

而对于有序的序列，我们可以采用二分法来解决。

2、代码实现

#include 
#include 
using namespace std;
const int N = 100010;
int a[N],q[N];
int n;
int main()
{
    scanf("%d", &n);
    //读入数据
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    
    int len = 0;//记录长度
    
    for (int i = 0; i < n; i ++ )
    {
        int l = 0, r = len;
        while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        //如果该元素插在了末尾，说明r+1=len+1了。此时长度增加，我们更新len 
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }
    printf("%d\n", len);
    return 0;
}