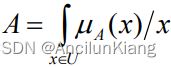《人工智能导论》 第1章 绪论&第2章 知识表示&第3章 确定性推理方法&第4章 不确定推理方法

绪论

人工智能的基本概念

智能的概念

目前对智能还没有确切的定义，主要流派有：

• 思维理论：智能的核心是思维，认为通过对思维规律与方法的研究可揭示智能的本质。
• 知识阈值理论：智能取决于知识的数量及一般化程度，认为智能是在巨大的搜索空间中迅速找到满意解的能力。
• 进化理论：用控制取代知识的表示，认为智能是某种复杂系统所浮现的性质。

综合上述观点可认为：智能是知识与智力的总和。其中知识是一切智能行为的基础，智力是获取知识求解问题的能力。

智能的特征

具有：

• 感知能力：通过视觉、听觉、触觉、嗅觉等感觉器官 感知外部世界的能力。80%以上信息通过视觉得到，10%信息通过听觉得到。
• 记忆能力：存储由感知器官感知到的外部信息以及由思维所产生的知识。
• 思维能力：对记忆的信息进行处理。
  • 逻辑思维：又称抽象思维。具有以下特征：
    • 依靠逻辑进行思维。
    • 思维过程是串行的。
    • 容易形式化。
    • 思维过程具有严密性、可靠性。
  • 形象思维：又称直感思维。具有以下特征：
    • 依据直觉。
    • 思维过程是并行协同式的。
    • 形式化困难。
    • 在信息变形或缺少的情况下仍有可能得到比较满意的结果。
  • 顿悟思维：又称灵感思维。具有以下特征：
    • 不定期的突发性。
    • 非线性的独创性及模糊性。
    • 穿插于形象思维与逻辑思维之中。
• 学习能力：既可能是自觉的、有意识的，也可能是不自觉的、无意识 的；既可以是有教师指导的，也可以是通过自己实践的。
• 行为能力：又称表达能力。用于信息的输出。

人工智能

定义

• 用人工的方法在机器（计算机）上实现的智能； 或者说是人们使机器具有类似于人的智能。人工智能学科是一门研究如何构造智能机器（智能计算机）或智能系统，使它能模拟、延伸、扩展人类智能的学科。
• 主要研究如何用人工的方法和技术，使用各种自动化机器或智能机器(主要指计算机)模仿、延伸和扩展人 的智能，实现某些机器思维或脑力劳动自动化。

为什么要研究人工智能

• 普通计算机智能低下，不能满 足社会需求。
• 研究人工智能也是当前信息化社会的迫切需求。
• 智能化是自动化发展的必然趋势。
• 研究人工智能， 对人类自身智能的奥秘也提供有益帮助。

研究目标

• 远期目标：制造具有完全智能的机器。
• 近期目标：实现机器智能。即先部分地或某种程度地实现机器智能，从而使现有的计算机更灵活好用和更聪明有用。

图灵测试

一种测试机器是不是具备人类智能的方法。图灵测试一词来源于计算机科学和密码学的先驱艾伦·麦席森·图灵写于1950年的一篇论文《计算机器与智能》。

具体来说，指如果一个人（代号C）使用测试对象皆理解的语言去询问两个他不能看见的对象任意一串问题。对象为：一个是正常思维的人（代号B）、一个是机器（代号A）。如果经过若干询问以后，C不能得出实质的区别来分辨A与B的不同，则此机器A通过图灵测试。

中文屋

美国哲学家约翰·希尔勒在1980年设计的一个思维试验以推翻强人工智能（机能主义）提出的过强主张：只要计算机拥有了适当的程序，理论上就可以说计算机拥有它的认知状态以及可以像人一样地进行理解活动。

这个实验要求你想象一位只说英语的人身处一个房间之中，这间房间除了门上有一个小窗口以外，全部都是封闭的。他随身带着一本写有中文翻译程序的书。房间里还有足够的稿纸、铅笔和橱柜。写着中文的纸片通过小窗口被送入房间中。根据Searle，房间中的人可以使用他的书来翻译这些文字并用中文回复。虽然他完全不会中文，Searle认为通过这个过程，房间里的人可以让任何房间外的人以为他会说流利的中文。

人工智能发展简史

孕育

在人工智能诞生之前，一些著名科学家就已经创立了数理逻辑、 神经网络模型和控制论，并发明了通用电子数字计算机。为人工智能的诞生准备了必要的思想、理论和物质技术条件。

• 亚里斯多德：三段论
• 培根：归纳法
• 莱布尼茨：万能符号、推理计算。
• 布尔：用符号语言描述思维活动的基本推理法则
• 图灵：图灵机
• 阿塔纳索夫：世界上第一台通用电子计算机ABC
• 麦克洛奇和匹兹：M-P模型

形成

1956年夏，麦卡锡和明斯基、洛切斯特、香农共同发起，邀请莫尔和塞缪尔、塞尔夫里奇、索罗莫夫以及纽厄尔、西蒙等10名年轻学者在达特莫斯大学召开了两个月的学术研讨会，讨论机器智能问题。会上经麦卡锡提议正式采用“人工智能”这一术语，标志着人工智能学科正式诞生。麦卡锡因而被称为人工智能之父。

1956年以后，人工智能的研究在机器学习、定理 证明、模式识别、问题求解、专家系统及人工智能语言等方面都取得了许多引人瞩目的成就 。

1969 年 ， 成立了国际人工智能联合会议。

1970年，创刊了国际性的人工智能杂志。

发展

20世纪60年代末，人工智能研究遇到困难，如机器翻译。 1966年美国顾问委员会的报告裁定：还不存在通用的科学文 本机器翻译，也没有很近的实现前景。英国、美国中断了大 部分机器翻译项目的资助。

1977年，费根鲍姆在第五届国际人工智能联合会议上提出了 “知识工程”概念，推动了知识为中心的研究。

1981年，日本宣布第五代计算机发展计划，并在1991年展出了研制的PSI－3智能工作站和由PSI－3构成的模型机系统。

我国自1978年开始把“智能模拟”作为国家科学技术发展规划的主要研究课题。1981年成立了中国人工智能学会。

现在，人工智能已经成为计算机、航空航天、军事装备、工业等众多领域的关键技术。

人工智能研究

基本内容

• 知识表示：将人类知识形式化或者模型化。
• 符号表示法：用各种包含具体含义的符号，以各种不同 的方式和顺序组合起来表示知识的一类方法。例如，一 阶谓词逻辑、产生式等。
• 连接机制表示法：把各种物理对象以不同的方式及顺序 连接起来，并在其间互相传递及加工各种包含具体意义 的信息，以此来表示相关的概念及知识。例如，神经网络等。
• 机器感知：使机器（计算机）具有类似于人的感知能力。 以机器视觉(machine vision)与机器听觉为主。
• 机器思维：对通过感知得来的外部信息及机器内部的各种工作信息进行有目的的处理。
• 机器学习：研究如何使计算机具有 类似于人的学习能力，使它能通过学习自动地获取知识。
  • 1957年，Rosenblatt研制成功了感知机。
• 机器行为：计算机的表达能力，即“说”、“写”、 “画”等能力。

主要领域

• 自动定理证明：定理证明的实质是证明由前提P得到结论Q的永真性。
  • 1958年，王浩证明了有关命题演算的全部定理（220 条）、谓词演算中150条定理的85%。
  • 1965年，鲁宾逊提出了归结原理，使机 器定理证明成为现实。
  • 吴文俊院士把几何代数化，建立了一套机器证明方法，被称为“吴方法”。
• 博弈：下棋、打牌、战争等一类竞争性的智能活动。
  • 1956年，塞缪尔研制出跳棋程序。
  • 1991年8月，IBM公司研制的Deep Thought 2计算机 系统与澳大利亚象棋冠军约翰森（D.Johansen）举行了 一场人机对抗赛，以1：1平局告终。
  • 1997年5月11日，IBM公司的超级计算机“深蓝”仅用了一小时便轻松击败了国际象棋特级大师卡斯帕罗夫。
  • 2016年3月，AlphaGo击败韩国九段棋手李世石。
• 模式识别：研究对象描述和分类方法的学科。分析和识别的模式可以是信号、 图象或者普通数据。
• 机器视觉：用机器代替人眼睛进行测量和判断。
• 自然语言理解：研究如何让计算机理解人类自然语言，包括回答问题、 生成摘要、翻译等。
• 智能信息检索：功能：
  • 能理解自然语言。
  • 具有推理能力。
  • 系统拥有一定的常识性知识。
• 数据挖掘与知识发现：从数据库中找出有意义的模式(一组规则、聚类、决策树、依赖网络或其他方式表示的知识)。数据挖掘过程：
  • 数据预处理
  • 建模
  • 模型评估及模型应用
• 专家系统：模拟人类专家求解问题的思维过程求解领域内的各种问题，其水平可以达到甚至超过人类专家的水平。
  • 1965年费根鲍姆研究小组开始研制第一个专家系统——分析化合物分子结构的DENDRAL，1968年完成并投入使用。
  • 1971年MIT开发成功求解一些数学问题的MYCSYMA专家系统。拉特格尔大学开发的清光眼诊断与治疗的专家系统CASNET。
  • 1972年斯坦福大学肖特里菲等人开始研制用于诊断和治疗感染性疾病的专家系统MYCIN。
  • 1976年斯坦福研究所开始开发探矿专家系统PROSPECTOR，1980年首次实地分析华盛顿某山区地质资料，发现了一个钼矿。
  • 1981年斯坦福大学研制成功专家系统AM，能模拟人类进行概括、抽象和归纳推理，发现某些数论的概念和定理。
• 自动程序设计：用户只需要告诉计算机要“做什么”， 无须说明“怎么做”，计算机就可自动实现程序的设计。
• 机器人：程序控制机器人（第一代） 、自适应机器人（第二代）、智能机器人（现代）。
• 组合优化问题：旅行商问题、生产计划与调度、物流中的车辆调度、智能交通、通信中的路由调度、计算机网络信息调度等。
• 人工神经网络：用大量简单处理单元经广泛连接而组成的人工网络，用来模拟大脑神经系统的结构和功能。
• 分布式人工智能与多智能体：以鲁棒性作为控制系统质量的标准，并具有互操作性，即不同的异构系统在快速变化的环境中，具有交换信息和协同工作的能力。
• 智能控制：同时具有知识表示的非数学广义世界模 型和传统数学模型混合表示的控制过程。
  • 专家智能控制
  • 模糊控制
  • 神经网络控制。
• 智能仿真：利用AI对整个仿真过程（建模、实验运行及结果分析） 进行指导。
• 智能CAD：把人工智能技术引入计算机辅助设计领域，至少有以下四个方面：
  • 设计自动化
  • 智能交互
  • 智能图形学
  • 自动数据采集
• 智能CAI：ICAI系统一般 分成专门知识、教导策略和学生模型和自然语言的智能接口。具备下列智能特征：
  • 自动生成各种问题与练习。
  • 根据学生的学习情况自动选择与调整教学内容与进度。
  • 在理解教学内容的基础上自动解决问题生成解答。
  • 具有自然语言生成和理解能力。
  • 对教学内容有理解咨询能力。
  • 能诊断学生错误，分析原因并采取纠正措施。
  • 能评价学生的学习行为。
  • 能不断地在教学中改善教学策略。
• 智能管理与智能决策：提高计算机管理系统的智能水平， 以及智能管理系统的设计理论、方法与实现技术。
• 智能多媒体系统：综合处理文字、图形、图像和声音 等多种媒体信息的计算机系统。
• 智能操作系统：以智能机为基础，能支撑外层的 AI应用程序，实现多用户的知识处理和并行推理。三大特点：
  • 并行性
  • 分布性
  • 智能性
• 智能计算机系统：从基本元件到体系结构，从处理对象到编 程语言，从使用方法到应用范围，同当前的诺依曼型计算机相 比，都有质的飞跃和提高，它将全面支持智能应用开发，且自身就具有智能。
• 智能通信：是在通信系统的各个层次和环节上实现智能化。
• 智能网络系统：将人工智能技术引入计算机网络系 统。如在网络构建、网络管理与控制、信息检索与转换、 人机接口等环节，运用AI的技术与成果。
• 人工生命：是以计算机为研究工具，模拟自然界的生命 现象，生成表现自然生命系统行为特点的仿真系统。

知识表示

知识与知识表示的概念

知识的概念

知识是在长期的生活及社会实践中、在科学研究及实验 中积累起来的对客观世界的认识与经验。

知识是把有关信息关联在一起所形成的信息结构。

知识反映了客观世界中事物之间的关系，不同事物或者相同事物间的不同关系形成了不同的知识。

知识的特性

• 相对正确性
  • 任何知识都是在一定的条件及环境下产生的，在 这种条件及环境下才是正确的。
• 不确定性
  • 随机性引起的不确定性
  • 模糊性引起的不确定性
  • 经验引起的不确定性
  • 不完全性引起的不确定性
• 可表示性和可利用性
  • 知识的可表示性: 知识可以用适当形式表示出来，如 用语言、文字、图形、神经网络等。
  • 知识的可利用性: 知识可以被利用。

知识的表示

知识表示（knowledge representation）：将人类知识形式 化或者模型化。知识表示是对知识的一种描述，或者说是一组约定，一 种计算机可以接受的用于描述知识的数据结构。选择知识表示方法的原则：

• 充分表示领域知识。
• 有利于对知识的利用。
• 便于对知识的组织、维护与管理。
• 便于理解与实现。

一阶谓词逻辑表示法

命题

• 非真即假：命题（proposition）：一个非真即假的陈述句。
• 可真可假：若命题的意义为真，称它的真值为真，记为 T。若命题的意义为假，称它的真值为假，记为 F。
• 时真时假： 一个命题可在一种条件下为真，在另一种条件下为假。
• 命题逻辑：研究命题及命题之间关系的符号逻辑系统。其局限性：
  • 无法把它所描述的事物的结构及逻辑特 征反映出来，也不能把不同事物间的共同特征表述出来。

谓词

谓词的一般形式：$P(x_1,x_2,\cdot \cdot \cdot ,x_n)$，

• $P$是谓词名，刻画个体的性质、状态或个体间的关系。
• $x_1,x_2,\cdot \cdot \cdot ,x_n$是个体，某个独立存在的事物或者某个抽象的概念。
  • 个体是常量：一个或者一组指定的个体。
    • 一元谓词：“老张是个教师”：$Teacher(Zhang)$
    • 二元谓词：“$5>3$”：$Greater(5,3)$
    • 三元谓词：“Smith作为一个工程师为IBM工作”：$Works(Smith,IBM,engineer)$
  • 个体是变元（变量）：没有指定的一个或者一组个体。
    • "$x<5$ "：$Less(x,5)$
  • 个体是函数：一个个体到另一个个体的映射。
    • “小李的父亲是教师”：$Teacher(father(Li))$
  • 个体是谓词
    • 二阶谓词：“Smith作为一个工程师为IBM工作”：$Works(engineer(Smith),IBM)$

谓词公式

• 连接词

  • $\neg$：称为“否定”或“非”，表取反。
  • $\vee$：称为“析取”，表或。
  • $\wedge$：称为“合取”，表与。
  • $\to$：称为“蕴含”或“条件”，表如果···则···。
  • $\leftrightarrow$：称为“等价”或“双条件”，表···当且仅当···。

• 量词

  • 全称量词 $\forall$：$\forall x$表示对个体 域中的所有（或任一个）个体 $x$。
  • 存在量词 $\exists$：$\exists x$表示在个体域中存在个体 $x$。

• 谓词公式：可按下述规则得到谓词演算的谓词公式：

  1. 单个谓词是谓词公式，称为原子谓词公式。
  2. 若 $A$ 是谓词公式，则 $\neg A$ 也是谓词公式。
  3. 若 $A$，$B$ 都是谓词公式，则 $A\wedge B$，$A\vee B$，$A\to B$， $A\leftrightarrow B$也都是谓词公式。
  4. 若A是谓词公式，则 $(\forall x)A$，$(\exists x)B$也是谓词公式。
  5. 有限步应用1 - 4生成的公式也是谓词公式。
  6. 连接词的优先级自低到高排序：$\lnot \ \land \ \lor \ \rightarrow \ \leftrightarrow $

• 量词的辖域：位于量词后面的单个谓词或者用括弧括起来的谓词公式。

  • 辖域内与量词中同名的变元称为约束变元。
  • 辖域内与量词中不同名的变元称为自由变元。

谓词公式的性质

• 谓词公式的解释：对命题公式中各个命题变元的一次真值指派称为一个解释。对于每一个解释，谓词公式都可求出一个真值（T 或F）。

• 谓词公式的永真性、可满足性、不可满足性：

  • 如果谓词公式 P 对个体域 D上的任何一个解释都取得真值 T，则称 P 在 D上是永真的；如果 P 在每个非空个体域上均永真，则称 P 永真。
  • 如果谓词公式 P 对个体域 D 上的任何一个解释都取得真值 F，则称 P 在 D 上是永假的；如果 P 在每个非空个体域上均永假，则称 P 永假。
  • 对于谓词公式 P，如果至少存在一个解释使得P在此解释下的真值为 T，则称 P 是可满足的，否则，则称 P 是不可满足的。

• 谓词公式的等价性：设 P 与 Q 是两个谓词公式，D 是它们共同的个 体域，若对 D 上的任何一个解释，P 与 Q 都有相同的真值，则称公式 P 和 Q 在 D 上是等价的。如果 D 是任意个体域，则称 P 和 Q 是等价的，记为$P⟺Q$。主要等价式：

  • 交换律
    $$\begin{gathered} P\vee Q⟺Q\vee P \\ P\wedge Q⟺Q\wedge P \end{gathered}$$

  • 结合律
    $$\begin{gathered} (P\vee Q)\vee R⟺P\vee (Q\vee R) \\ (P\wedge Q)\wedge R⟺P\wedge (Q\wedge R) \end{gathered}$$

  • 分配律
    $$\begin{gathered} P\vee (Q\wedge R)⟺(P\vee Q)\wedge (P\vee R) \\ P\wedge (Q\vee R)⟺(P\wedge Q)\vee (P\wedge R) \end{gathered}$$

  • 德摩根律
    $$\begin{gathered} \neg (P\vee Q)⟺\neg P\wedge \neg Q \\ \neg (P\wedge Q)⟺\neg P\vee \neg Q \end{gathered}$$

  • 双重否定律
    $$\neg \neg P⟺P$$

  • 吸收律
    $$\begin{gathered} P\vee (P\wedge Q)⟺P \\ P\wedge (P\vee Q)⟺P \end{gathered}$$

  • 补余律
    $$\begin{gathered} P\vee \neg P⟺T \\ P\wedge \neg P⟺F \end{gathered}$$

  • 连接词划归律
    $$P\to Q⟺\neg P\vee Q$$

  • 逆否律
    $$P\to Q⟺Q\to \neg P$$

  • 量词转化律
    $$\begin{gathered} \neg (\exists x)P⟺(\forall x)(\neg P) \\ \neg (\forall x)P⟺(\exists x)(\neg P) \end{gathered}$$

  • 量词分配律
    $$\begin{gathered} (\forall x)(P\wedge Q)⟺(\forall x)P\wedge (\forall x)Q \\ (\exists x)(P\vee Q)⟺(\exists x)P\vee (\exists x)Q \end{gathered}$$

• 谓词公式的永真蕴含：对于谓词公式 P 与 Q，如果 $P\to Q$ 永真，则称 公式 P 永真蕴含 Q，且称 Q 为 P 的逻辑结论，称 P 为 Q 的前提，记为$P⟹Q$。

  • 假言推理
    $$P,P\to Q⟹Q$$

  • 拒取式推理
    $$\neg Q,P\to Q⟹\neg P$$

  • 假言三段论
    $$P\to Q,Q\to R⟹P\to R$$

  • 全称固化
    $$(\forall x)P(x)⟹P(y)$$

  • 存在固化
    $$(\exists x)P(x)⟹P(y)$$

  • 反证法：$Q$ 为 $P_1,P_2,\cdot \cdot \cdot ,P_n$ 的逻辑结论，当且仅当 $(P_1\wedge P_2\wedge \cdots \wedge P_n)$ 是不可满足的。

一阶逻辑知识表示方法

谓词公式表示知识的一般步骤：

1. 定义谓词及个体。
2. 变元赋值。
3. 用连接词连接各个谓词，形成谓词公式。

一阶逻辑谓词表示法的特点

优点：

• 自然性
• 精确性
• 严密性
• 容易实现

局限性：

• 不能表示不确定的知识
• 组合爆炸
• 效率低

产生式表示法

产生式

• 确定性规则知识的产生式表示
  $$\begin{gathered} IFPTHENQ \\ 或 \\ P\to Q \end{gathered}$$

• 不确定性规则知识的产生式表示
  $$\begin{gathered} IFPTHENQ(置信度) \\ 或 \\ P\to Q(置信度) \end{gathered}$$

• 确定性事实性知识的产生式表示
  $$\begin{gathered} (对象,属性,值) \\ 或 \\ (关系,对象1,对象2) \end{gathered}$$

• 不确定性事实性知识的产生式表示
  $$\begin{gathered} (对象,属性,值,置信度) \\ 或 \\ (关系,对象1,对象2,置信度) \end{gathered}$$

• 产生式与谓词逻辑中的蕴含式的区别：

  • 除逻辑蕴含外，产生式还包括各种操作、规则、 变换、算子、函数等。例如， “如果炉温超过上限，则立即关闭风门”是一个产生式，但不是蕴含式。
  • 蕴含式只能表示精确知识，而产生式不仅可以表 示精确的知识，还可以表示不精确知识。蕴含式的 匹配总要求是精确的。产生式匹配可以是精确的， 也可以是不精确的，只要按某种算法求出的相似度 落在预先指定的范围内就认为是可匹配的。

• 产生式的形式描述及语义——巴科斯范式
  $$\begin{gathered} <产生式>::=<前提>\to <结论> \\ <前提>::=<简单条件>\mid <复合条件> \\ <结论>::=<事实>\mid <操作> \\ <复合条件>::=<简单条件>AND<简单条件>\cdots \mid <简单条件>OR<简单条件>\cdots \\ <操作>::=<操作名>[(<变元>,\cdots )] \end{gathered}$$

产生式系统

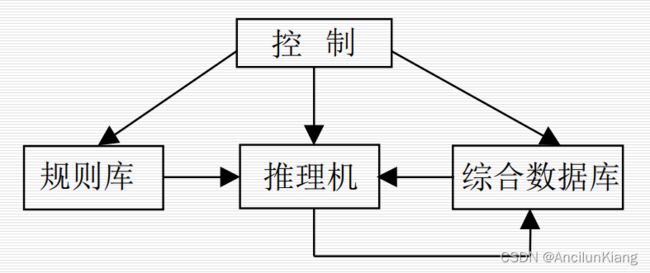
一般来说，产生式系统由规则库、控制系统(推理机)、综合数据库三部分组成：

• 规则库：用于描述相应领域内知识的产生式集合。
• 综合数据库：用于存放问题求解过程中各种当前信息的数据结构。
• 控制系统(推理机构)：由一组程序组成，负责整个 产生式系统的运行，实现对问题的求解。控制系统要做以下几项工作：
  • 从规则库中选择与综合数据库中的已知事实进行匹配。
  • 匹配成功的规则可能不止一条，进行冲突消解。
  • 执行某一规则时，如果其右部是一个或多个结论，则把这些结论加入到综合数据库中：如果其右部是一个或多个操作， 则执行这些操作。
  • 对于不确定性知识，在执行每一条规则时还要按一定的算法计算结论的不确定性。
  • 检查综合数据库中是否包含了最终结论，决定是否停止系统的运行。

动物识别系统

$$\begin{array}{rl}& r_1：IF该动物有毛发THEN该动物是哺乳动物\\ & r_2：IF该动物有奶THEN该动物是哺乳动物\\ & r_3：IF该动物有羽毛THEN该动物是鸟\\ & r_4：IF该动物会飞AND会下蛋THEN该动物是鸟\\ & r_5：IF该动物吃肉THEN该动物是食肉动物\\ & r_6：IF该动物有犬齿AND有爪AND眼盯前方THEN该动物是食肉动物\\ & r_7：IF该动物是哺乳动物AND有蹄THEN该动物是有蹄类动物\\ & r_8：IF该动物是哺乳动物AND是反刍动物THEN该动物是有蹄类动物\\ & r9：IF该动物是哺乳动物AND是食肉动物AND是黄褐色AND身上有暗斑点THEN该动物是金钱豹\\ & r10：IF该动物是哺乳动物AND是食肉动物AND是黄褐色AND身上有黑色条纹THEN该动物是虎\\ & r11：IF该动物是有蹄类动物AND有长脖子AND有长腿AND身上有暗斑点THEN该动物是长颈鹿\\ & r12：IF该动物有蹄类动物AND身上有黑色条纹THEN该动物是斑马\\ & r13：IF该动物是鸟AND有长脖子AND有长腿AND不会飞AND有黑白二色THEN该动物是鸵鸟\\ & r14：IF该动物是鸟AND会游泳AND不会飞AND有黑白二色THEN该动物是企鹅\\ & r15：IF该动物是鸟AND善飞THEN该动物是信天翁\end{array}$$

产生式表示法的特点

• 产生式表示法的优点:
• 自然性
• 模块性
• 有效性
• 清晰性
• 产生式表示法的缺点:
  • 效率不高
  • 不能表达结构性知识
• 适合产生式表示的知识:
  • 领域知识间关系不密切， 不存在结构关系。
  • 经验性及不确定性的知 识，且相关领域中对这些知识没有严格、统一的理论。
  • 领域问题的求解过程可 被表示为一系列相对独立的操作，且每个操作可被表示为一 条或多条产生式规则。

框架表示法

• 框架（frame）：一种描述所论对象（一个事物、事 件或概念）属性的数据结构。
• 一个框架由若干个被称为“槽”（slot）的结构组成， 每一个槽又可根据实际情况划分为若干个“侧面” （faced）。
• 一个槽用于描述所论对象某一方面的属性。
• 一个侧面用于描述相应属性的一个方面。
• 槽和侧面所具有的属性值分别被称为槽值和侧面值。

框架的一般结构：

确定性推理方法

推理的基本概念

• 推理的定义：从初始证据出发，按某种策略不断运用知识库中的已有知识，逐步推出结论的过程称为推理。

• 推理方式及其分类：

  • 按推出结论的途径划分：
    • 演绎推理：由一般到个别，常用三段论法：
      • 大前提：已知的一般性知识或假设。
      • 小前提：关于所研究的具体情况或个别事实的新判断。
      • 结论：由大前提推出的适合小前提所示情况的新判断。
    • 归纳推理：由个别到一般，分为：
      • 完全归纳推理
      • 不完全归纳推理
    • 默认推理：知识不完全的情况下假设某些条件已经具备所进行的推理。
  • 按推理时所用知识的确定性划分：
    • 确定性推理：推理时所用的知识与证据都是确定的， 推出的结论也是确定的，其真值或者为真或者为假。
    • 不确定性推理：推理时所用的知识与证据不都是确定 的，推出的结论也是不确定的。
      • 似然推理
      • 近似推理或模糊推理
  • 按推理过程中推出的结论对目标的趋近性划分：
    • 单调推理：随着推理向前推进及新知识的加入，推出的结论越来越接近最终目标。
    • 非单调推理：由于新知识的加入，不仅没有加强已 推出的结论，反而要否定它，使推理退回到前面的某一步，重新开始。
  • 按推理过程中是否运用启发性知识划分：
    • 启发式推理与非启发式推理：是否运用与推理有关的启发性知识。
      • 启发性知识：与问题有关且能加快推理过程、提高搜索效率的知识。

• 推理的方向：

  • 正向推理：由已知事实到结论。
  • 逆向推理：以某个假设目标作为出发点。
  • 混合推理：正反向混合推理
    • 先正向后逆向：先进行正向推理，帮助选择某个目标， 即从已知事实演绎出部分结果，然后再用逆向推理证实该目标 或提高其可信度。
    • 先逆向后正向：先假设一个目标进行逆向推理，然后再 利用逆向推理中得到的信息进行正向推理，以推出更多的结论。
  • 双向推理：正向推理与逆向推理同时进行，且在推理过程 中的某一步骤上“碰头”的一种推理。

• 三种匹配情况：

  • 恰好匹配成功（一对一）
  • 不能匹配成功
  • 多种匹配成功（一对多、多对一、多对多）

• 冲突消解策略：

  • 按针对性排序
  • 按已知事实的新鲜性排序
  • 按匹配度排序
  • 按条件个数排序

自然演绎推理

从一组已知为真的事实出发，运用经典 逻辑的推理规则推出结论的过程。

• P 规则
• T 规则
• 假言推理
• 拒取式推理

归结演绎推理

• 原子（atom）谓词公式： 一个不能再分解的命题。
• 文字（literal）：原子谓词公式及其否定。
• 正文字：$P$
• 负文字：$\neg P$
• 子句（clause）：任何文字的析取式。任何文字本身 也都是子句。
• 空子句（NIL）：不包含任何文字的子句。
• 子句集：由子句构成的集。

谓词公式化为子句集的方法

1. 消去谓词公式中的 $\rightarrow $ 和 $\leftrightarrow $ 符号
2. 把否定符号 $\lnot $ 移到紧靠谓词的位置上
3. 变量标准化
4. 消去存在量词
5. 化为前束形
6. 化为 Skolem 标准形
7. 略去全称量词
8. 消去合取词
9. 子句变量标准化

鲁宾逊归结原理

• 基本思想：
  • 检查子句集 $S$ 中是否包含空子句，若包含，则 $S$ 不可满足。
  • 若不包含，在 $S$ 中选择合适的子句进行归结，一旦归结出空 子句，就说明 $S$ 是不可满足的。
• 归结：设 $C_1$ 与 $C_2$ 是子句集中的任意两个子句，如果 $C_1$ 中的文字 $L_1$ 与 $C_2$ 中的文字 $L_2$ 互补，那么从 $C_1$ 和 $C_2$ 中分别消去 $L_1$ 和 $L_2$ ，并将二个子句中余下的部分析取，构成一个新 子句 $C_{12}$ 。
• 归结式 $C_{12}$ 是其亲本子句 $C_1$ 与 $C_2$ 的逻辑结论。即如果 $C_1$ 与 $C_2$ 为真，则 $C_{12}$ 为真。
  • $S_1$ 的不可满足性$\Longrightarrow $$S$ 的不可满足性
  • $S_2$ 的不可满足性$\Longrightarrow $$S$ 的不可满足性

归结反演

应用归结原理证明定理的过程称为归结反演。 用归结反演证明的步骤是：

1. 将已知前提表示为谓词公式 $F$ 。
2. 将待证明的结论表示为谓词公式 $Q$ ，并否定得到 $\neg Q$ 。
3. 把谓词公式集 $\{F,\neg Q\}$ 化为子句集 $S$ 。
4. 应用归结原理对子句集 $S$ 中的子句进行归结，并把每次归结得到的归结式都并入到 $S$ 中。如此反复进行，若出现了空子句，则停止归结，此时就证明了 $Q$ 为真。

应用归结反演求解问题

应用归结原理求解问题的步骤：

1. 已知前提$F$ 用谓词公式表示，并化为子句集 $S$ 。
2. 把待求解的问题 $Q$ 用谓词公式表示，并否定$Q$ ，再与 $ANSWER$ 构成析取式$(\neg Q\vee ANSWER)$。
3. 把 $(\neg Q\vee ANSWER)$ 化为子句集，并入到子句集 $S$ 中， 得到子句集 $S ’ $ 。
4. 对 $S ’ $应用归结原理进行归结。
5. 若得到归结式 $ANSWER$ ，则答案就在 $ANSWER$中。

不确定性推理方法

不确定性推理的基本概念

不确定性推理：从不确定性的初始证据出发，通过运用不确定性的知识，最终推出具有一定程度的不确定性但却是合理或者近乎合理的结论的思维过程。

• 不确定性的表示与量度：
  • 知识不确定性的表示
  • 证据不确定性的表示
  • 不确定性的量度
    • 能充分表达相应知识及证据不确定性的程度。
    • 度量范围的指定便于领域专家及用户对不确定性的估计。
    • 便于对不确定性的传递进行计算，而且对结论算出的不确 定性量度不能超出量度规定的范围。
    • 度量的确定应当是直观的，同时应有相应的理论依据。
• 不确定性匹配算法及阈值的选择
  • 不确定性匹配算法：用来计算匹配双方相似程度的算法。
  • 阈值：用来指出相似的“限度” 。
• 组合证据不确定性的算法：
• 最大最小方法
• Hamacher方法
• 概率方法
• 有界方法
• Einstein方法等
• 不确定性的传递算法
  • 在每一步推理中，如何把证据及知识的不确定性传递给结论。
  • 在多步推理中，如何把初始证据的不确定性传递给最终结论。

可信度方法

• 知识不确定性的表示，C-F模型
  $$IFETHENH(CF(H,E))$$
  其中，$(CF(H,E))$表示可信度因子，反映前提条件与结论的联系强度，其取值范围为[-1,1]。

• 证据不确定性的表示
  $$CF(E)$$
  $CF(E)$的取值范围也为[-1,1]。

• 组合证据不确定性的算法

  • 多个单一证据的合取取最小值
    $$\begin{gathered} E=E_{1}AND{E}_{2}AND\cdots AND{E}_n \\ 则CF(E)=\min \{CF(E_1),CF(E_2),\cdots ,CF(E_n)\} \end{gathered}$$

  • 多个单一证据的析取取最大值
    $$\begin{gathered} E=E_{1}OR{E}_{2}OR\cdots OR{E}_n \\ 则CF(E)=\max \{CF(E_1),CF(E_2),\cdots ,CF(E_n)\} \end{gathered}$$

• 不确定性的传递算法
  $$CF(H)=CF(H,E)\times \max \{0,CF(E)\}$$

• 结论不确定性的合成算法

  1. 分别对每一条知识求出$CF(H)$

  2. 求出$E_1$​与$E_2$​对H的综合影响所形成的可信度 $C{F}_{1,2}(H)$​：
     $$\begin{array}{c}C{F}_{1,2}(H)=\{\begin{array}{rlrl}& C{F}_1(H)+C{F}_2(H)-C{F}_1(H)C{F}_2(H)& & C{F}_1(H)\ge 0,C{F}_2(H)\ge 0\\ & C{F}_1(H)+C{F}_2(H)+C{F}_1(H)C{F}_2(H)& & C{F}_1(H)<0,C{F}_2(H)<0\\ & \frac{C{F}_1(H)+C{F}_2(H)}{1-\{|C{F}_1(H)|,|C{F}_2(H)|\}}& & C{F}_1(H)C{F}_2(H)<0\end{array}\end{array}$$

证据理论

• 样本空间：设 $D$ 是变量 $x$ 所有可能取值的集合，且 $D$ 中的元素是互斥的，在任一时刻 $x$ 都取且只能取$D$ 中的某一个元素为值，则称 $D$ 为 x 的样本空间。

• 概率分配函数：设 $D$ 为样本空间，领域内的命题都用 $D$ 的子集表示， 设函数 $M:2^D\to [0,1]$，即对任何一个属于$D$ 的子集A，命它对应一个数 $M\in [0,1]$，且满足：
  $$\begin{gathered} M(\varnothing )=0 \\ \sum _{A\subseteq D}M(A)=1 \end{gathered}$$
  则称$M$是 $2^D$ 上的基本概率分配函数，$M(A)$称为A的基本概率数。

  • 设样本空间 $D$ 中有n个元素，则 $D$ 中子集的个数为$2^n$个，定义中的 $2^D$ 就是表示这些子集的。
  • 概率分配函数的作用是把$D$的任意一个子集A都映射为[0,1]上的一个数 $M(A)$ 。
  • 概率分配函数与概率不同。

• 信任函数：命题的信任函数（belief function）$Bel:2^D\to [0,1]$，且
  $$Bel(A)=\sum _{B\subseteq A}M(B)\forall A\subseteq D$$
  其中$2^D$表示$D$的所有子集。

  $Bel$ 函数又称为下限函数， $Bel(A)$ 表示对命题A为真的总的信任度。

• 似然函数：不可驳斥函数或上限函数。似然函数$Pl:2^D\to [0,1]$，且
  $$Pl(A)=1-Bel(\neg A)\forall A\subseteq D$$
  Pl(A)表示对A为非假的信任程度。

• 概率分配函数的正交和（证据的组合）：设 $M_1$ 和 $M_2$ 是两个概率分配函数，则其正交和 $M=M_1\oplus M_2$ 为
  $$\begin{array}{rl}& M(\varnothing )=0\\ & M(A)=K^{-1}\sum _{x\cap y=A}{M}_1(X)M_2(y)\end{array}$$
  其中$K$由下式计算
  $$K=1-\sum _{x\cap y=\varnothing }{M}_1(x)M_2(y)=\sum _{x\cap y=\varnothing }{M}_1(x)M_2(y)$$

  • 如果$K\ne 0$ ，则正交和 M也是一个概率分配函数。
  • 如果 $K=0$，则不存在正交和 $M$，即没有可能存在概 率函数，称 $M_1$ 与 $M_2$ 矛盾。

• 基于证据理论的不确定性推理的步骤：

  1. 建立问题的样本空间 $D$。
  2. 由经验给出，或者由随机性规则和事实的信度度量算基本概率分配函数。
  3. 计算所关心的子集的信任函数值、似然函数值。
  4. 由信任函数值、似然函数值得出结论。

模糊推理方法

• 模糊集合的定义

  • 论域：所讨论的全体对象，用 $U$ 等表示。
  • 元素：论域中的每个对象，常用 $a,b,c,x,y,z$ 表示。
  • 集合：论域中具有某种相同属性的确定的、可以彼此区别的元素的全体，常用$A$，$B$等表示。
  • 元素$a$和集合$A$的关系：$a$属于$A$或$a$不属于$A$，即只有两个真值 “真”和“假” 。
  • 模糊逻辑给集合中每一个元素赋予一个介于0和1之间的实数， 描述其属于一个集合的强度，该实数称为元素属于一个集合的隶属度。集合中所有元素的隶属度全体构成集合的隶属函数。

• 模糊集合的表示方法：当论域中元素数目有限时，模糊集合A的数学描述为$A=\{(x,{\mu }_A(x),x\in X\}$，其中${\mu }_A(x)$表示元素$x$属于模糊集$A$的隶属度， 是元素$x$的论域。

  • Zadeh表示法

    • 论域离散且元素数目有限：
      $$\begin{gathered} A={\mu }_A(x_1)/x_1+{\mu }_A(x_2)/x_2+\cdots +{\mu }_A(x_n)/x_n=\sum _{i=1}^n{\mu }_A(x_i)/x_i \\ 或 \\ A=\{{\mu }_A(x_1)/x_1,{\mu }_A(x_2)/x_2,\cdots ,{\mu }_A(x_n)/x_n\} \end{gathered}$$

    • 论域连续或者元素数目无限：

      

      该符号并非积分号，不好打出来。

  • 序偶表示法
    $$A=\{({\mu }_A(x_1),x_1),({\mu }_A(x_2),x_2),\cdots ,({\mu }_A(x_n),x_n)\}$$

  • 向量表示法
    $$A=\{{\mu }_A(x_1),{\mu }_A(x_2),\cdots ,{\mu }_A(x_n)\}$$

• 隶属函数：模糊集合中所有元素的隶属度全体构成模糊集合的隶属函数。常见的隶属函数有正态分布、三角分布、梯形分布等。隶属函数确定方法：

  • 模糊统计法
  • 专家经验法
  • 二元对比排序法
  • 基本概念扩充法

• 模糊集合的运算

  • 模糊集合的包含关系
    • 若${\mu }_A(x)\ge {\mu }_B(x)$，则$A\supseteq B$。
  • 模糊集合的相等关系
    • 若${\mu }_A(x)={\mu }_B(x)$，则$A=B$。
  • 模糊集合的交并补运算
    • KaTeX parse error: Undefined control sequence: \and at position 52: …B(x)\}=\mu_A(x)\̲a̲n̲d̲\mu_B(x)
    • KaTeX parse error: Undefined control sequence: \or at position 52: …B(x)\}=\mu_A(x)\̲o̲r̲\mu_B(x)
    • KaTeX parse error: Got function '\overline' with no arguments as subscript at position 5: \mu_\̲o̲v̲e̲r̲l̲i̲n̲e̲{A}(x)=1-\mu_A(…
  • 模糊集合的代数运算
    • 代数积：${\mu }_{AB}(x)={\mu }_A(x){\mu }_B(x)$
    • 代数和：${\mu }_{A+B}(x)={\mu }_A(x)+{\mu }_B(x)-{\mu }_{AB}(x)$
    • 有界和：${\mu }_{A\oplus B}(x)=\min \{1,{\mu }_A(x)+{\mu }_B(x)\}=1\wedge [{\mu }_A(x)+{\mu }_B(x)]$
    • 有界积：${\mu }_{A\otimes B}(x)=\max \{0,{\mu }_A(x)+{\mu }_B(x)-1\}=0\vee [{\mu }_A(x)+{\mu }_B(x)-1]$

• 模糊关系与模糊关系的合成

  • 模糊关系：设$A$、$B$为两个模糊集合，模糊关系用叉积(cartesian product)表示。在模糊逻辑中，这种叉积常用最小算子运算，即：
    $${\mu }_{A\times B}(a,b)=\min \{{\mu }_A(a),{\mu }_B(b)\}$$
    若$A$、$B$为离散模糊集，其隶属函数分别为：
    $$\begin{gathered} {\mu }_A=[{\mu }_A(a_1),{\mu }_A(a_2),\cdots ,{\mu }_A(a_n)] \\ {\mu }_B=[{\mu }_A(b_1),{\mu }_A(b_2),\cdots ,{\mu }_A(b_n)] \end{gathered}$$
    则叉积运算为：
    $${\mu }_{A\times B}(a,b)={\mu }_A^T\circ {\mu }_B$$
    其中$\circ$为模糊向量乘积。

  • 模糊关系的合成：设模糊关系$Q\in X\times Y，R\in Y\times Z$，则模糊关系$S\in X\times Z$称为模糊关系$Q$与$R$的合成。模糊关系$Q$与$R$的合成$S$是模糊矩阵的叉乘$S=Q\circ R$。模糊矩阵的合成常用一下几种计算方法：

    • 最大-最小合成法：写出矩阵乘积$QR$中的每个元素，然后将其中的乘积运算用取小运算代替，求和运算用取大运算代替。
    • 最大-代数积合成法：写出矩阵乘积$QR$中的每个元素，然后将其中的求和运算用取大运算代替，而乘积运算不变。