【论文精读】MVSDF: Learning Signed Distance Field for Multi-view Surface Reconstruction
这是一篇ICCV2021的文章。
项目地址:Github
论文地址:arxiv
文章目录
- Abstract
- 1 Introduction
- 2 Related Works
- 3 Method
-
- 3.1 Geometry and Appearance Representations
-
- Differentiable Surface Intersection
- 3.2 Geometry Supervision
-
- Multi-view Depth Map Estimation
- Direct SDF Supervision
- Signed Distance Fusion in a Mini-batch
- 3.3 Local Geometry Refinement
-
- Feature Consistency
- Rendered Image Consistency
- 3.4 Valid Surface Indicator
- 3.5 Loss
- 4 Experiments
-
- 4.1. Implementation
- 4.2. Benchmark on DTU Dataset
- 4.3. Benchmark on EPFL Dataset
- 4.4. Additional Qualitative Results
- 4.5. Ablation Study
- 5 Conclusion
Abstract
最近关于隐式神经表示的研究在多视图表面重建方面显示出了有希望的结果。 然而,大多数方法仅限于相对简单的几何形状,并且通常需要干净的对象mask来重建复杂和凹面对象。 在这项工作中,我们引入了一种新颖的神经表面重建框架,该框架利用立体匹配和特征一致性的知识来优化隐式表面表示。 更具体地说,我们应用有符号距离场(SDF)和表面光场分别表示场景几何形状和外观。 SDF由立体匹配的几何结构直接监督,并通过优化多视图特征一致性和渲染图像的保真度进行细化。 我们的方法能够提高几何估计的鲁棒性并支持复杂场景拓扑的重建。 在 DTU、EPFL 以及 Tanks 和 Temples 数据集上进行了大量实验。 与之前最先进的方法相比,我们的方法在没有掩模作为输入的情况下在广阔的开放场景中实现了更好的网格重建。
1 Introduction
传统上,表面重建可以分为两个子步骤:1)通过多视图立体(MVS)算法从图像重建深度图和点云; 2)表面,通常表示为三角形网格,通过最大化与点的一致性从密集点中提取。 或者,可以应用表面细化步骤通过多视图照片一致性来恢复几何细节。虽然该流程已被证明在各种情况下都是有效且稳健的,但由于从图像到点再到网格的表示转换中的累积损失,重建的几何形状可能不是最佳的。 例如,点云重建中引入的错误会传递到表面重建,导致错误的网格拓扑并且难以恢复。 尽管最近提出了基于学习的 MVS 和网格提取方法来独立提高每个子步骤的重建质量,但仍然希望以端到端的方式从图像重建最佳表面。
另外,最近关于神经表示的工作表明,可以通过隐式表示和可微渲染从图像直接构造网格表面。 场景的表面几何和颜色信息通常表示为隐函数,由网络中的多层感知器(MLP)直接建模,并通过可微渲染进行优化。 可以通过Marching Cube 算法从隐式场中提取三角形网格。 与经典的网格划分管道相比,这些方法能够以端到端的方式重建场景几何形状并同时生成合成图像。然而,由于所有场景参数同时联合优化,几何图形只是整个差分渲染管线的副产品,几何图形和外观存在模糊性。 为了缓解这个问题,隐式可微渲染器(IDR)应用手动标记的对象mask作为输入,但对于大量图像来说这是不可行的,并且有时对于现实世界的图像输入没有很好的定义。
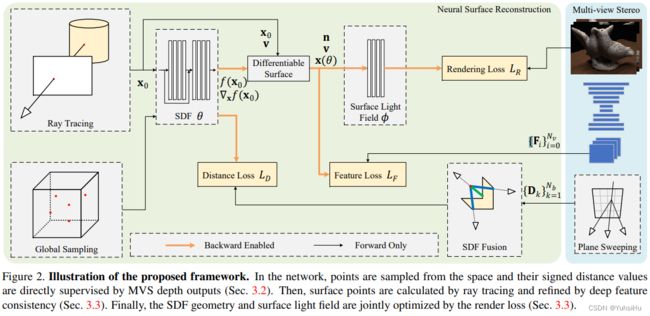
在本文中,我们提出了 MVSDF,一种新颖的神经表面重建框架,它将隐式神经表面估计与最新先进的 MVS 网络相结合。 一方面,我们遵循隐式可微渲染器将表面表示为有符号距离场(SDF)的零水平集,并将外观表示为表面光场,这通过渲染损失来联合优化。 另一方面,我们从基于学习的 MVS 引入深度图像特征和深度图来辅助隐式 SDF 估计。 SDF 由 MVS 网络推断的深度值进行监督,并通过最大化 SDF 表面点的多视图特征一致性来进一步细化。 我们发现,在 MVS 深度图的指导下,可以极大地改善表面拓扑,并且即使没有输入对象mask,我们的方法也可以应用于复杂的几何形状。 此外,与 IDR 中的渲染损失相比,多视图特征一致性在可微渲染管道的早期阶段施加了光度约束,这显着提高了几何精度,并有助于在最终重建中保留高保真细节。
2 Related Works
主要介绍了MVS和Implicit Neural Surface、Surface Reconstruction by Differentiable Rendering的相关工作。
我们的方法与 IDR 最相关,它使用 SDF 和表面光场作为场景表示。 这两个隐式网络通过渲染损失联合训练,并应用图像mask进行约束 SDF 优化。 然而,IDR 的重建质量很大程度上取决于输入mask的准确性,不准确的mask可能会导致网格表面丢失或冗余。 由于自动对象分割方法并不总是完美的,IDR应用手动标记的mask来确保重建质量。 在这项工作中,我们引入多视图立体和特征一致性作为我们的几何约束,以提高表面质量并放宽图像mask的要求。
3 Method
3.1 Geometry and Appearance Representations
表面 S θ S_{\theta} Sθ被作为了SDF的零集合,在网络中由一个MLP f f f来表示。我们定义这个 θ \theta θ是 f f f中一个可以学习的参数。这个MLP会把查询的位置 x x x作为输入,然后输出一个该位置到达最近的表面上的点的距离。
受 IDR 的启发,我们的场景外观由表面光场表示,使用另一个具有可学习参数 ϕ \phi ϕ 的 MLP g g g。 表面光场以查询表面点 x x x、其法线向量 n n n和视线 v v v的单位向量作为输入,并输出查询的RGB颜色 c c c。
渲染时,通过球体追踪得到视线与表面的交点,点法线可计算为隐式表面的解析梯度 n = ∇ x f ( x ; θ ) n = ∇xf(x; θ) n=∇xf(x;θ)。
Differentiable Surface Intersection
球体追踪在网络中不是可微操作。 像之前的工作一样,我们构造了从网络参数到交叉点位置的函数的一阶近似。 对于当前网络参数 θ 0 \theta_{0} θ0、视射线 v v v 以及该射线上的交点 x 0 x_{0} x0,我们对方程 f ( x ; θ ) ≡ 0 f(x; θ) ≡ 0 f(x;θ)≡0 进行隐式微分,surface intersection可以表示为 θ \theta θ 的函数:

其中 f ( x 0 ; θ 0 ) f(x_{0}; θ_{0}) f(x0;θ0) 和 ∇ x f ( x 0 ; θ 0 ) ∇xf(x_{0}; θ_{0}) ∇xf(x0;θ0) 是常数。
3.2 Geometry Supervision
多视图立体算法能够提供高质量的深度图作为场景的密集表示。 在本节中,我们将描述如何使用 MVS 深度图来监督 SDF 优化
Multi-view Depth Map Estimation
在我们的网络中,MVS 模块旨在为所有输入图像生成深度图像特征和合格的深度图。 我们应用开源 Vis-MVSNet 作为我们的深度生成模块。 对于参考图像及其相邻源图像,首先应用标准UNet来提取深度图像特征图。 然后,所有特征图将被扭曲到参考图像的相机视锥体中并构造3D成本体积C。我们进一步通过3D CNN对成本体积进行正则化,并通过softmax获得深度样本的概率分布。 最后,通过取深度期望从概率体积回归深度 D 0 D_{0} D0。 此外,对于深度图中的像素 p p p,我们评估其在预测深度值周围的概率和 P ( p ) P(p) P(p),作为深度置信度的指标。 置信度低的像素将被过滤掉,以生成干净的深度图。
Direct SDF Supervision
之前的工作提出通过最小化追踪深度图和GT深度图之间的差异来训练隐式网络。 然而,这种策略只能影响当前表面估计附近的网络输出。 为了确保 SDF 在整个空间中正确恢复,我们从整个空间中随机采样点并计算采样点到 MVS 深度图的距离。
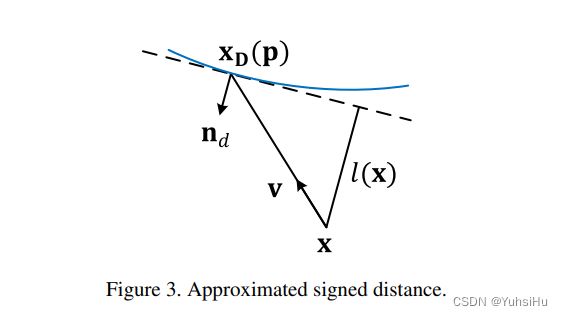
给定一个采样点 x x x和深度图 D D D,我们首先把 x x x投影在投影到深度图上的p点。然后我们将 MVS 深度 D ( p ) D(p) D(p) 在与 x D ( p ) x_{D}(p) xD(p) 相同的位置反投影到空间。 如图3所示,从 x x x到MVS表面的符号距离近似为:

其中 n d n_{d} nd 是根据深度计算的法线。 此外,如果概率和 P ( p ) P(p) P(p) 小于阈值 T p r o b T_{prob} Tprob,我们认为该像素位于背景中,并将从距离计算中排除对应点。 这个近似的有符号距离可以用来监督SDF训练,我们将距离损失 L D L_{D} LD定义为:
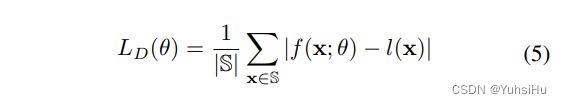
其中 S S S是有效的采样点。
Signed Distance Fusion in a Mini-batch
等式5的一个问题是从单个深度图计算出的近似符号距离 l ( x ) l(x) l(x)通常不可靠。 首先,自由空间中的采样点可能在给定视图中被遮挡。 其次,当出现非平面表面时,近似的 l ( x ) l(x) l(x) 可能不准确。 为了提高 l ( x ) l(x) l(x) 的准确性,我们在训练期间将 N b N_{b} Nb 个视图分组到一个小批量中,并且将通过融合小批量内 N b N_{b} Nb 个深度图的多个观测值来细化 l ( x ) l(x) l(x)。
对于查询点 x x x,我们首先计算每个深度图中其近似符号距离 { l k ( x ) } k = 1 N b \{l_{k}(x)\}^{N_{b}}_{k=1} {lk(x)}k=1Nb。 根据 l k ( x ) l_{k}(x) lk(x) 的符号,如果距 { l k ( x ) } k = 1 N b \{l_{k}(x)\}^{N_{b}}_{k=1} {lk(x)}k=1Nb 的至少 T o u t T_{out} Tout 距离为正,则定义点位于曲面之外。 确定查询点在内部或外部后,我们收集具有相同符号的每个视图距离,并将最小深度距离作为融合距离 l ( x ) l(x) l(x)的绝对值。 我们发现这种简单的融合策略可以有效地从单个深度图中过滤掉错误的观测值,并且融合后的 l ( x ) l(x) l(x) 足够准确,可以用来指导 SDF 优化。
3.3 Local Geometry Refinement
第 3.2 节中的几何监督可以正确恢复表面拓扑。 然而,由于 MVS 网络的深度图通常有噪声,因此在最终的网格重建中恢复表面细节相当困难。 为此,我们建议在网络训练过程中优化特征一致性和渲染图像一致性。
Feature Consistency
在传统的 MVS 或网格重建流程中,密集点云或网格表面通常通过多视图光度一致性优化来细化。表面点的光度一致性被定义为多个视图之间的匹配成本(例如 ZNCC)。 在我们的工作中,请注意,Vis-MVSNet 中已经提取了深层图像特征。 相反,我们最小化多视图深度特征一致性。
Rendered Image Consistency
渲染图像一致性在最近的可微分渲染pipeline中被广泛使用。 对于图像中的像素 p p p,我们可以在空间中追踪其表面交点 x x x。 通过将 x ( θ ) x(θ) x(θ)、 ∇ x f ( x ; θ ) ∇_{x}f(x; θ) ∇xf(x;θ) 和 v v v 输入到函数 g g g 中,可以直接从表面光场获取像素 p p p 的渲染颜色 c ( p ) c(p) c(p)。 然后将渲染损失计算为从渲染颜色到输入图像颜色的 L1 距离。
渲染损失可以共同优化几何形状 θ θ θ 和外观 φ φ φ。 与 L F L_{F} LF 相比, L R L_{R} LR 对局部颜色变化更加敏感,在恢复高保真表面细节方面发挥着重要作用。
3.4 Valid Surface Indicator
如果输入图像不能完全覆盖感兴趣的对象,则看不见的区域的表面将不能很好地定义,并且往往会在背景区域中产生外推表面。 为了区分这种无效表面,我们使用另一个指示函数来标记是否可以从某些输入视图中跟踪空间点。 具体地,函数h(x;γ)表示x在有效表面中的指示符。 在每次训练迭代期间,成功追踪位置的指标 {x +} 被设置为 1。为了防止 h(x; γ) 到处都报告为 1,我们还在空间中随机采样点 {x −} 并将背景指标设置为 0 .然后我们应用二元交叉熵作为我们的指标损失:

请注意,我们的 MVS 深度图是使用相应的概率图进行过滤的,并且我们不会对这些过滤后的像素应用光线追踪。 因此,MVS 深度图中的过滤区域往往会被分配背景指示符 0。换句话说,我们可以根据过滤后的 MVS 深度图来识别无效的表面区域。
3.5 Loss
4 Experiments
介绍了具体的实现和实验结果,感兴趣的可以自行查看。
4.1. Implementation
4.2. Benchmark on DTU Dataset
4.3. Benchmark on EPFL Dataset
4.4. Additional Qualitative Results
4.5. Ablation Study
5 Conclusion
在这项工作中,我们引入了一种新颖的神经表面重建框架,它将隐式神经表面估计与最新先进的 MVS 网络相结合。 在我们的网络中,几何形状和外观由 MLP 表示为神经隐式函数。 几何结构由 MVS 深度图直接监督以恢复表面拓扑,并通过深度特征一致性和渲染图像损失进行局部细化。 所提出的方法已在不同的数据集上进行了广泛的评估。 定性和定量结果都表明,我们的方法在几何精度和渲染保真度方面都优于以前的方法,证明了所提出框架的有效性。