《动手学深度学习 Pytorch版》 4.8 数值稳定性和模型初始化

4.8.1 梯度消失和梯度爆炸

整节理论，详见书本。

1. 梯度消失

%matplotlib inline
import torch
from d2l import torch as d2l

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.sigmoid(x)
y.backward(torch.ones_like(x))

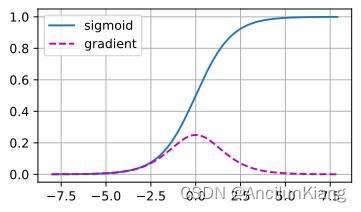
d2l.plot(x.detach().numpy(), [y.detach().numpy(), x.grad.numpy()],
         legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))

# 可以观察到当 sigmoid 函数的输入极大或极小时梯度会消失。

​

​

2. 梯度爆炸

M = torch.normal(0, 1, size=(4,4))
print('一个矩阵\n', M)
for i in range(100):
    M = torch.mm(M, torch.normal(0, 1, size=(4, 4)))

print('乘以100个矩阵后\n', M)

一个矩阵
 tensor([[-0.0548,  0.0265,  0.4826, -2.4794],
        [ 2.0281,  1.1197,  1.7950,  0.1482],
        [ 2.5176,  0.5329, -1.8411, -0.3951],
        [-0.4566, -0.1391, -1.1882,  0.0556]])
乘以100个矩阵后
 tensor([[-4.8657e+18, -7.5395e+18, -3.0949e+18,  1.2648e+18],
        [ 9.8213e+21,  1.1332e+22,  3.4642e+21, -7.3061e+21],
        [-6.0221e+21, -6.9359e+21, -2.1151e+21,  4.4953e+21],
        [-5.1453e+21, -5.9341e+21, -1.8129e+21,  3.8310e+21]])

4.8.2 参数初始化

整节理论，详见书本。

练习

（1）除了多层感知机的排列具有对称性之外，还能设计出其他神经网络可能会表现出对称性且需要被打破的情况吗？

不会，略。

---

（2）我们是否可以将线性回归或 softmax 回归中的所有参数初始化为相同的值？

会因永远无法打破对称性而永远无法实现网络的表达能力。

---

（3）在相关资料中查找两个矩阵乘积特征值的解析解。这对确保梯度条件合适有什么启示？

不会，略。

---

（4）如果我们知道某些项是发散的，我们能在事后修正吗？可以参考关于按层自适应速率缩放的论文。

“某些项是发散的”没看明白，不会，略。