Python 遗传算法求解多目标单模式资源受限项目调度问题(MORCPSP)的帕累托前沿
系列文章目录
目录
系列文章目录
前言
一、概念介绍
1.1 鲁棒性
1.2 工期
二、模型的建立
三、算法的确定
3.1 染色体的编码
3.2 染色体的选择
3.3 染色体的交叉
3.4 染色体的变异
四、代码的实现
五、结果分析
总结
前言
我前面有博客已经探讨了如何解决单目标、单模式的资源受限项目调度问题并附上了代码,本篇博客旨在解决以项目的鲁棒性、工期为双目标的单模式资源受限项目调度问题,博客内提供了相应的部分代码。
想获得全部代码,可以加我创立的qq群下载群文件,群号:808756207。本群旨在研究工程管理、工商管理等管理学算法的代码化,借助计算机技术规范管理学的研究。我会不定期上传一些我自己研究的管理学python代码,以及其他国内外大佬的python代码。
一、概念介绍
1.1 鲁棒性
根据论文:Lambrechts O, Demeulemeester E, Herroelen W. A tabu search procedure for developing robust predictive project schedules. International Journal of Production Economics, 2008, 111(2): 493–508. 的描述,项目的鲁棒性的概念大致可以理解为:项目的鲁棒性等于各个活动的鲁棒性之和,而每个活动的鲁棒性又等于本活动的总时差(最早开始时间减最晚开始时间)乘以本活动的累积不稳定权重,而每个活动的累积不稳定权重又等于本活动的不稳定权重加上该活动的所有紧后活动的不稳定权重。
为了计算方便,本文对所有活动的不稳定权重都取0.1。
因此,通俗的讲,大部分情况下拥有紧后活动数量多的活动的累积不稳定权重自然就大,我们就越应该给这样的活动多分配一些总时差,因为它们影响的紧后活动比较多。一旦这些活动出了些问题,对整个项目的影响也是最大的。
我们当然希望鲁棒性越大越好,这样整个项目就越加稳定。同时鲁棒性跟接下来要提到的工期大体上是负相关的关系。
1.2 工期
这个概念无需多言,作为一个项目经理,我们自然是希望手里的这个项目的工期越短越好。但是结合上面提到的鲁棒性的概念,工期太短的项目稳定性越差,即鲁棒性越小。如何找到鲁棒性、工期这两个目标间的平衡点就是本篇博客研究的主要内容。
二、模型的建立
模型的表达方式还是按照我之前博客确定的字典格式(或称为Json格式)。这种格式的优点在于,表达清晰、信息比较好通过代码读取。
project={
1:{"successors":[2, 3, 4, 5],"predecessors":[],"duration":0,"resource_request":[0, 0, 0, 0]},
2:{"successors":[6],"predecessors":[1],"duration":2,"resource_request":[0, 1, 0, 0]},
3:{"successors":[10],"predecessors":[1],"duration":4,"resource_request":[0, 0, 0, 3]},
4:{"successors":[9],"predecessors":[1],"duration":6,"resource_request":[0, 0, 2, 0]},
5:{"successors":[11],"predecessors":[1],"duration":9,"resource_request":[0, 0, 7, 0]},
6:{"successors":[7],"predecessors":[2],"duration":8,"resource_request":[0, 0, 5, 0]},
7:{"successors":[8, 11],"predecessors":[6],"duration":10,"resource_request":[3, 0, 0, 0]},
8:{"successors":[12],"predecessors":[7],"duration":4,"resource_request":[0, 0, 0, 7]},
9:{"successors":[12],"predecessors":[4],"duration":3,"resource_request":[3, 0, 0, 0]},
10:{"successors":[12],"predecessors":[3],"duration":5,"resource_request":[0, 0, 6, 0]},
11:{"successors":[12],"predecessors":[5, 7],"duration":1,"resource_request":[0, 9, 0, 0]},
12:{"successors":[],"predecessors":[8, 9, 10, 11],"duration":0,"resource_request":[0, 0, 0, 0]},
"total_resource": [3, 9, 9, 9]
}
其中,“2:{"successors":[6],"predecessors":[1],"duration":2,"resource_request":[0, 1, 0, 0]}”代表该项目中活动序号为2的活动的紧后活动为活动6,活动序号为2的活动的紧前活动为活动1,活动序号为2的活动的工期为2,这个活动运行时使用的四种资源的状况为[0, 1, 0, 0]。以此类推。同时,"total_resource": [3, 9, 9, 9]表示这个项目的四种资源的总量为:[3, 9, 9, 9]。
三、算法的确定
本算法的灵感来源于论文:李雪,何正文,王能民.考虑鲁棒性成本的多模式双目标项目前摄性调度优化[J].系统工程学报,2021,36(01):74-87.
大致思路为两层循环的嵌套求解帕累托前沿。外层循环控制变量为项目的工期,内层循环控制变量就是迭代次数。即通过检索每个工期的最大鲁棒性的值来获得帕累托前沿。
3.1 染色体的编码
我之前博客用的编码方式为混合编码,详细内容可以看下我之前的博客。后来我突然悟道(哭笑)离散编码的方式似乎能完成我们的算法需要,并且更快捷。编码方式如下
[0,1,3,4,6,9,12]每个整型的数字代表项目中各个活动的开始时间,其中数字9就代表序号为6的活动的开始时间,因为对列表从左往右数,数字9刚好在第6位。但是有一点需要注意,大部分编程语言(除了MATLAB这种古董)的列表的索引都是从0开始的。所以,项目活动的序号比其对应列表的索引是大1的,这点很关键很关键。
至于活动的结束时间,我们则可以通过我们刚才建立的项目的Json模型,通过映射关系得到项目的工期,然后由项目的开始时间+工期得到项目的结束时间。
3.2 染色体的选择
选择这块没啥难点,就采用普通的二元竞标选择即可。
3.3 染色体的交叉
由于我们采用了离散编码的方式,并且列表的索引代表着对应的活动序号,所以交叉操作比较简单,没什么难点,直接交叉就行。
我之前采用的混合编码,交叉的操作很复杂。还需要用的PMX算子(部分匹配交叉算子)。这种离散编码的方式就很便捷。
3.4 染色体的变异
难点来了。我发现用遗传算法解决问题,最难的部分当属变异算子了。此外就是编码(因为编码直接决定你后续的编程难度和代码的效率,所以选择编码的时候要谨慎)。
我采用单点变异的方式。难点在于,每一次对一个染色体基因进行变异后,还要进行后续的验算,保证这个变异是合法的。验算什么内容呢?第一、验算变异后的染色体是否满足资源限量的要求。第二、用递归的方式验算变异后的染色体,是否满足活动间的紧前、紧后关系,如果不满足,当前活动的紧后活动的开始时间就需要向后移,一直移到不能在移为止,也就是收敛到最优解了。难就难在这个递归怎么写,但是我写出来了(哈哈)。
四、代码的实现
本博客贴出的是部分代码,要获得所有代码,请加群:808756207,部分代码如下:
"""
---写在前面---
项目的鲁棒性,根据某论文中的理论,是等于各个活动的鲁棒性之和
而每个活动的鲁棒性又等于本活动的总时差(最早开始时间-最晚开始时间)乘以本活动的累积不稳定权重
而每个活动的累积不稳定权重又等于本活动的不稳定权重加上该活动的所有紧后活动的不稳定权重
为了计算方便,本文对所有活动的不稳定权重都取0.1
因此,拥有紧后活动数量多的活动的累积不稳定权重自然就大
[[1,0,0],[2,0,2],[4,3,6],[3,8,10],[5,10,10]]
活动1的紧后活动为活动2,活动1的总时差为0
活动2的紧后活动为活动3和活动4,活动2的总时差为0
活动3的紧后活动为活动5,活动3的总时差为1
活动4的紧后活动为活动5,活动4的总时差为0
活动5没有紧后活动,活动5的总时差为0
鲁棒性=0*(0.1+0.1)+0*(0.1*3)+1*(0.1+0.1)+0*(0.1+0.1)+0*(0.1+0.1)=0.2
writen by 二开金城武
"""
import copy
import random
import numpy as np
import matplotlib.pyplot as plt
project={
1:{"successors":[2, 3, 4, 5],"predecessors":[],"duration":0,"resource_request":[0, 0, 0, 0]},
2:{"successors":[6],"predecessors":[1],"duration":2,"resource_request":[0, 1, 0, 0]},
3:{"successors":[10],"predecessors":[1],"duration":4,"resource_request":[0, 0, 0, 3]},
4:{"successors":[9],"predecessors":[1],"duration":6,"resource_request":[0, 0, 2, 0]},
5:{"successors":[11],"predecessors":[1],"duration":9,"resource_request":[0, 0, 7, 0]},
6:{"successors":[7],"predecessors":[2],"duration":8,"resource_request":[0, 0, 5, 0]},
7:{"successors":[8, 11],"predecessors":[6],"duration":10,"resource_request":[3, 0, 0, 0]},
8:{"successors":[12],"predecessors":[7],"duration":4,"resource_request":[0, 0, 0, 7]},
9:{"successors":[12],"predecessors":[4],"duration":3,"resource_request":[3, 0, 0, 0]},
10:{"successors":[12],"predecessors":[3],"duration":5,"resource_request":[0, 0, 6, 0]},
11:{"successors":[12],"predecessors":[5, 7],"duration":1,"resource_request":[0, 9, 0, 0]},
12:{"successors":[],"predecessors":[8, 9, 10, 11],"duration":0,"resource_request":[0, 0, 0, 0]},
"total_resource": [3, 9, 9, 9]
}
# 种群初始化操作,我想用离散编码的方式,即列表中的元素表示的是每个活动的开始时间,列表的索引+1是活动的序号
project = {
"total_resource": [3, 9, 9, 9],
1: {"successors": [2, 3, 4, 5], "predecessors": [], "duration": 0, "resource_request": [0, 0, 0, 0]},
2: {"successors": [6], "predecessors": [1], "duration": 2, "resource_request": [0, 1, 0, 0]},
3: {"successors": [10], "predecessors": [1], "duration": 4, "resource_request": [0, 0, 0, 3]},
4: {"successors": [9], "predecessors": [1], "duration": 6, "resource_request": [0, 0, 2, 0]},
5: {"successors": [11], "predecessors": [1], "duration": 9, "resource_request": [0, 0, 7, 0]},
6: {"successors": [7], "predecessors": [2], "duration": 8, "resource_request": [0, 0, 5, 0]},
7: {"successors": [8, 11], "predecessors": [6], "duration": 10, "resource_request": [3, 0, 0, 0]},
8: {"successors": [12], "predecessors": [7], "duration": 4, "resource_request": [0, 0, 0, 7]},
9: {"successors": [12], "predecessors": [4], "duration": 3, "resource_request": [3, 0, 0, 0]},
10: {"successors": [12], "predecessors": [3], "duration": 5, "resource_request": [0, 0, 6, 0]},
11: {"successors": [12], "predecessors": [5, 7], "duration": 1, "resource_request": [0, 9, 0, 0]},
12: {"successors": [], "predecessors": [8, 9, 10, 11], "duration": 0, "resource_request": [0, 0, 0, 0]}
}
def initialize(project:dict,size:int,makespan:int):
population=[]
while len(population) 1:
for a in candidate_activities:
if a == len(project)-1:
candidate_activities.remove(a)
break
else:
early_start_time+=1
good_scheme=True
for gene in scheme[:-1]:
if gene >= scheme[-1]:
good_scheme=False
break
if good_scheme:
population.append(scheme)
return population
def _is_resource_enough(candidate_activity, early_start_time, assigned_activities, project:dict,scheme):
t = early_start_time + 1
while t <= early_start_time + project[candidate_activity]["duration"]:
sum_resource = np.zeros(len(project["total_resource"]))
for assigned_activity in assigned_activities:
if scheme[assigned_activity-1]+ 1 <= t <= scheme[assigned_activity-1] + project[assigned_activity]["duration"]:
sum_resource += project[assigned_activity]["resource_request"]
sum_resource += project[candidate_activity]["resource_request"]
if (sum_resource > np.array(project["total_resource"])).any():
return False
t += 1
return True
def _is_resource_enough_project(scheme, project):
total_resource=np.array(project["total_resource"]*(len(project)-1))\
.reshape((len(project)-1),len(project["total_resource"]))
avail_resource=copy.deepcopy(total_resource)
for i,gene in enumerate(scheme):
id=i+1
start=gene
end=start+project[id]["duration"]
avail_resource[start:end]-=project[id]["resource_request"]
if (avail_resource<0).any():
return False
return True
def _cross(parent1,parent2):
# 随机选择交叉区域
start, end = sorted(random.sample([x for x in range(1, len(parent1) - 1)], 2))
# 将父代1中交叉区域的基因复制到子代1和2中
child1 = parent1[:start] + parent2[start:end + 1] + parent1[end + 1:]
child2 = parent2[:start] + parent1[start:end + 1] + parent2[end + 1:]
return child1,child2
print("这里只是部分代码,加群免费下载群文件的完整代码即可,\n群号:808756207")
exit() 五、结果分析
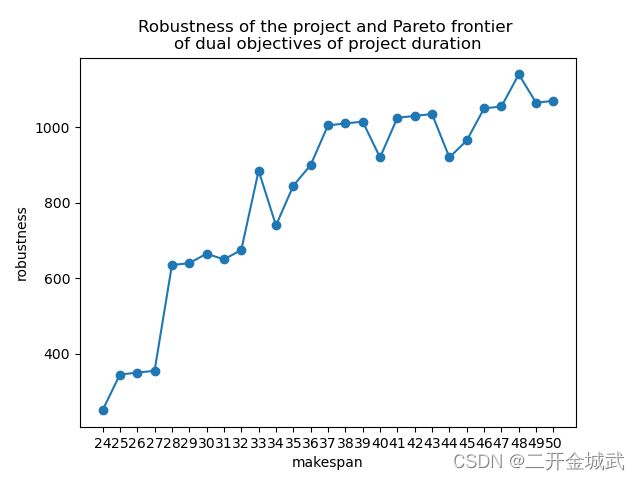
我通过python的 matplotlib.pyplot 绘制了这个帕累托前沿的离散曲线,形状如下:
横坐标为工期,纵坐标为鲁棒性。我们进行简单的敏感性分析可以发现,在工期为37时,鲁棒性已经达到了较高的水平,并且37之后的工期即使鲁棒性在提升,但是提升的变化幅度并不大。因此我作为项目经理,我大概率选择37作为我项目的工期。如果还是嫌37太长了,我们也可以考虑工期33,因为33相当于一个局部的极值点,在工期较短的情况下还能保证一个相对较高的鲁棒性。
总结
第一、我这次算法采用的是离散编码的方式,这点很重要。第二、请加我的群,我们一起讨论,集思广益,做大做强,再创辉煌。这点更重要。