使用python实现C4.5决策树并使用treelib输出
实验目的
本实验的主要目的是采用C4.5算法建立决策树模型,通过计算每个特征的信息增益率来评估其对于分类的重要性,进而构建一个能够对数据进行分类的决策树模型,并将最终的决策树模型以结构图的形式展示出来,以便更好地理解和分析模型的分类决策过程。
实验原理
C4.5算法是一种决策树分类算法,它是基于ID3算法改进而来的。C4.5算法相较于ID3算法具有更好的鲁棒性和更高的分类准确度,它主要有以下特点:
- 决策树生成:C4.5算法采用自顶向下的贪心策略生成决策树,首先将全部训练数据看作一个根节点,然后将训练数据分成多个子集,每个子集对应一个子节点,这个分裂过程一直进行到叶子节点。
- 特征选择:C4.5算法采用信息增益率来选择最优特征。信息增益率是信息增益与分裂信息之比,它可以消除信息增益对特征取值较多的偏好。
- 剪枝:C4.5算法采用后剪枝策略,即将生成的决策树进行剪枝,以消除过度拟合的影响,提高决策树的泛化能力。
C4.5算法的具体步骤如下:
- 根据训练数据集,计算每个特征的信息增益率,并选择信息增益率最大的特征作为当前节点的分裂特征。
- 根据分裂特征的取值,将训练数据集分成多个子集,并为每个子集创建一个子节点。
- 对于每个子节点,如果它所包含的样本都属于同一类别,或者它所包含的样本的特征已经处理完毕,则将其设置为叶子节点,否则重复步骤1。
- 对生成的决策树进行后剪枝,直到决策树无法再剪枝为止。
C4.5算法相较于ID3算法在处理连续特征时更加简单,同时可以处理缺失值问题,但是在处理大量特征时会面临过拟合的风险
实验内容
-
定义计算整体的信息熵
def getAllE(x): count = [] res = [] cate = set(x) for item in cate: temp = 0 for j in range(len(x)): if x[j] == item: temp += 1 temp = temp / len(x) res.append(-temp * math.log(temp, 2)) count.append(temp / len(x)) return sum(res)- 通过
set(x)获取特征取值的不重复集合,即特征的所有可能取值。 - 遍历不重复集合中的每个取值 item,在列表 x 中统计 item 出现的次数,计算 item 在 x 中的出现频率 temp。
- 计算该特征取值的信息熵,即对所有不同取值 item 的
-p(item)*log2(p(item))进行求和,其中 p(item) 表示 item 在 x 中的出现频率。 - 返回所有特征取值的信息熵之和。
- 通过
-
定义计算属性条件熵
def getEntropy(x, fin, choice=1): cate = set(x) fincate = set(fin) # 结果的类别 count = [] # 每个类别的数量 catepro = [] # 每个类别所占的比例 finpro = [] # 每个类别对应结果的比例 # 计算 for item in cate: temp = 0 cateFin = [] # 存取每个类别对应的结果 for i in range(len(x)): if x[i] == item: temp += 1 cateFin.append(fin[i]) # 每个类别对应的结果类数 cateFinSet = set(cateFin) finArr = [] for item in cateFinSet: # 如果该类别的结果与外层循环相等 lis = [j for j in cateFin if j == item] finArr.append(len(lis) / len(cateFin)) # 可以得到该类别下不同结果所占的比例 finpro.append(finArr) # 类别数量 count.append(temp) pro = temp / len(x) # 类别占的比例 catepro.append(pro) res = [] for i in range(len(catepro)): temp = 0 for j in range(len(finpro[i])): temp += -(finpro[i][j]) * math.log(finpro[i][j], 2) res.append(catepro[i] * temp) return sum(res)函数的输入参数包括x(样本的特征值)和fin(样本的标签),以及可选参数choice。函数首先用set(x)来得到样本的特征类别集合,然后用set(fin)得到标签类别集合。接着,它循环遍历每个特征类别,计算每个类别的样本数量,以及该类别中不同标签所占的比例(即样本属于该特征类别并且标签为某个标签的样本数量除以该特征类别的样本数量),并将这些比例存储在finpro列表中。然后,函数计算每个特征类别所占样本的比例,以及每个特征类别的信息熵。最后,将每个特征类别的信息熵与该类别所占样本的比例相乘,并对所有特征类别的结果求和,得到该特征的信息熵。该函数计算的是特征的信息熵,也称为条件熵,表示特征给定的条件下,样本的不确定性。
-
定义计算纯度
def getFineness(x, fin): cate = set(x) res = [] for item in cate: temp = [] for j in range(len(fin)): if item == x[j]: temp.append(fin[j]) temp = set(temp) temp = list(temp) if len(temp) == 1: res.append([int(item), True, int(temp[0])]) else: res.append([int(item), False]) print(res) return res该代码实现了对数据集特征x的精细化处理,即对于每一个不同的x值,查找其在结果集fin中的所有出现,将这些结果去重后存入一个列表中,如果列表中只有一个元素,则说明这个x值对应的结果是确定的;否则,说明这个x值对应的结果不唯一,需要继续对其进行分类处理。具体来说,该函数接收两个参数,一个是特征集合x,另一个是对应的结果集合fin,它的输出是一个列表,其中每个元素表示一个x值对应的信息。对于每个元素,第一个元素是x值本身,第二个元素是一个布尔类型的值,表示这个x值是否是唯一的结果;如果是唯一的结果,则还有第三个元素,表示这个结果的具体取值。最终输出这个列表。
-
定义决策树代码
def DecisionTree(data, fatherNode, notcul=[], nodeNname=''): # 需要做决策树分类的列数 cols = data.shape[1] - 1 # 整体信息熵 ED = getAllE(data[:, -1]) # 属性条件熵 E = [] # 分裂信息度量 H = [] # 信息增益 Gain = [] # 信息增益率 GainRatio = [] for i in range(cols): E.append(getEntropy(data[:, i], data[:, -1])) H.append(getAllE(data[:, i])) Gain.append(ED - E[i]) if H[i] != 0: GainRatio.append(Gain[i] / H[i]) else: GainRatio.append(0) num = len(notcul) if fatherNode != -1: print(tree.level(fatherNode)) num = tree.level(fatherNode) print(notcul) print(notcul[:num + 2]) # 选择信息增益率最大的作为节点 for item in notcul[:num + 2]: print("gainRatio赋零") GainRatio[item] = 0 print(GainRatio) maxIndex = GainRatio.index(max(GainRatio)) notcul.append(maxIndex) print("maxIndex:", maxIndex) if fatherNode == -1: tree.create_node(col_name[maxIndex], maxIndex) fatherNode = maxIndex else: if tree.get_node(maxIndex): tree.create_node(str(col_name[maxIndex]) + '-' + str(nodeNname), taglis[-1], parent=fatherNode) fatherNode = taglis[-1] taglis.pop() else: tree.create_node(str(col_name[maxIndex]) + '-' + str(nodeNname), taglis[-1], parent=fatherNode) fatherNode = taglis[-1] taglis.pop() child = getFineness(data[:, maxIndex], data[:, -1]) isover = True for i in range(len(child)): # 叶节点 if child[i][1] == True: tree.create_node(str(res_col_name[child[i][2] - 1]) + '-' + str(child[i][0]), taglis[-1], parent=fatherNode, data=child[i][2]) taglis.pop() # 树节点 else: data1 = copy.deepcopy(data) data2 = data1[data1[:, maxIndex] == child[i][0]] DecisionTree(data2, fatherNode=fatherNode, notcul=notcul, nodeNname=str(child[i][0])) isover = False if isover: return tree.show()参数:
- data:待分类的数据集,格式为一个二维数组,每行表示一个样本,每列表示一个特征。
- fatherNode:当前节点的父节点编号。
- notcul:已经被选择过的特征的编号。
- nodeNname:当前节点的名称。
功能:
- 计算每个特征的信息熵、条件熵、分裂信息度量、信息增益和信息增益率。
- 选择信息增益率最大的特征作为当前节点,并在决策树上创建该节点。
- 递归处理当前节点的子节点,直到所有叶子节点都被处理完。
具体解释:
cols = data.shape[1] - 1:获取数据集的列数,因为最后一列是标签列,不是特征列。ED = getAllE(data[:, -1]):计算数据集的整体信息熵。E、H、Gain、GainRatio:分别为属性条件熵、分裂信息度量、信息增益和信息增益率的列表。for i in range(cols)::循环遍历每个特征,计算它们的信息熵、分裂信息度量、信息增益和信息增益率。num = len(notcul):获取已经被选择过的特征数。if fatherNode != -1::如果当前节点有父节点,则打印出父节点的层数、已经被选择过的特征和当前需要选择的特征。for item in notcul[:num + 2]::将已经被选择过的特征的信息增益率设置为0。maxIndex = GainRatio.index(max(GainRatio)):选择信息增益率最大的特征的编号。notcul.append(maxIndex):将选择的特征编号添加到已经被选择过的特征列表中。if fatherNode == -1::如果当前节点没有父节点,则在树的根节点创建新节点。else::如果当前节点有父节点,则在树上创建新节点。child = getFineness(data[:, maxIndex], data[:, -1]):根据选择的特征将数据集分成若干个子集。for i in range(len(child))::循环遍历每个子集。if child[i][1] == True::如果当前子集是叶节点,则在树上创建新叶子节点。else::如果当前子集不是叶节点,则递归处理该子集,将其作为当前节点的子节点。tree.show():在控制台上输出完整的决策树。
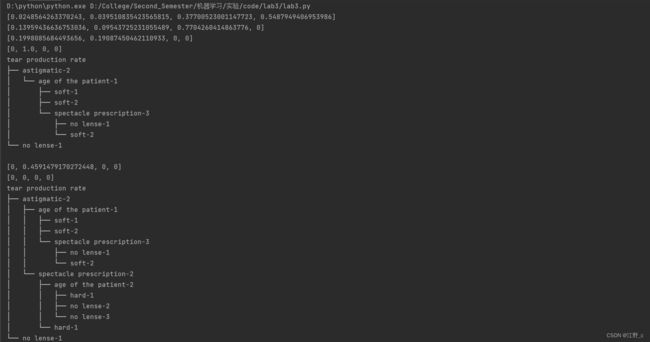
节点后的值表示,当父节点取该值时,会进入到该子节点
完整代码
import copy
import numpy as np
import math
from treelib import Tree
tree = Tree()
col_name = ['age of the patient', "spectacle prescription", "astigmatic", "tear production rate"]
res_col_name = ['hard', 'soft', 'no lense']
leaf = 100
taglis = [i for i in range(200)]
def getAllE(x):
count = []
res = []
cate = set(x)
for item in cate:
temp = 0
for j in range(len(x)):
if x[j] == item:
temp += 1
temp = temp / len(x)
res.append(-temp * math.log(temp, 2))
count.append(temp / len(x))
return sum(res)
def getEntropy(x, fin, choice=1):
cate = set(x)
fincate = set(fin) # 结果的类别
count = [] # 每个类别的数量
catepro = [] # 每个类别所占的比例
finpro = [] # 每个类别对应结果的比例
# 计算
for item in cate:
temp = 0
cateFin = [] # 存取每个类别对应的结果
for i in range(len(x)):
if x[i] == item:
temp += 1
cateFin.append(fin[i])
# 每个类别对应的结果类数
cateFinSet = set(cateFin)
finArr = []
for item in cateFinSet:
# 如果该类别的结果与外层循环相等
lis = [j for j in cateFin if j == item]
finArr.append(len(lis) / len(cateFin))
# 可以得到该类别下不同结果所占的比例
finpro.append(finArr)
# 类别数量
count.append(temp)
pro = temp / len(x)
# 类别占的比例
catepro.append(pro)
res = []
for i in range(len(catepro)):
temp = 0
for j in range(len(finpro[i])):
temp += -(finpro[i][j]) * math.log(finpro[i][j], 2)
res.append(catepro[i] * temp)
return sum(res)
def getFineness(x, fin):
cate = set(x)
res = []
for item in cate:
temp = []
for j in range(len(fin)):
if item == x[j]:
temp.append(fin[j])
temp = set(temp)
temp = list(temp)
if len(temp) == 1:
res.append([int(item), True, int(temp[0])])
else:
res.append([int(item), False])
return res
def DecisionTree(data, fatherNode, notcul=[], nodeNname=''):
# 需要做决策树分类的列数
cols = data.shape[1] - 1
# 整体信息熵
ED = getAllE(data[:, -1])
# 属性条件熵
E = []
# 分裂信息度量
H = []
# 信息增益
Gain = []
# 信息增益率
GainRatio = []
for i in range(cols):
E.append(getEntropy(data[:, i], data[:, -1]))
H.append(getAllE(data[:, i]))
Gain.append(ED - E[i])
if H[i] != 0:
GainRatio.append(Gain[i] / H[i])
else:
GainRatio.append(0)
num = len(notcul)
if fatherNode != -1:
num = tree.level(fatherNode)
# 选择信息增益率最大的作为节点
for item in notcul[:num + 2]:
GainRatio[item] = 0
print(GainRatio)
maxIndex = GainRatio.index(max(GainRatio))
notcul.append(maxIndex)
if fatherNode == -1:
tree.create_node(col_name[maxIndex], maxIndex)
fatherNode = maxIndex
else:
if tree.get_node(maxIndex):
tree.create_node(str(col_name[maxIndex]) + '-' + str(nodeNname), taglis[-1], parent=fatherNode)
fatherNode = taglis[-1]
taglis.pop()
else:
tree.create_node(str(col_name[maxIndex]) + '-' + str(nodeNname), taglis[-1], parent=fatherNode)
fatherNode = taglis[-1]
taglis.pop()
child = getFineness(data[:, maxIndex], data[:, -1])
isover = True
for i in range(len(child)):
# 叶节点
if child[i][1] == True:
tree.create_node(str(res_col_name[child[i][2] - 1]) + '-' + str(child[i][0]), taglis[-1], parent=fatherNode,
data=child[i][2])
taglis.pop()
# 树节点
else:
data1 = copy.deepcopy(data)
data2 = data1[data1[:, maxIndex] == child[i][0]]
DecisionTree(data2, fatherNode=fatherNode, notcul=notcul, nodeNname=str(child[i][0]))
isover = False
if isover:
return
tree.show()
if __name__ == '__main__':
data = np.loadtxt('./source/lenses_data.txt')
# 包括最后一列结果的数据
data = data[:, 1:]
DecisionTree(data, -1)
# tree.create_node(