栈和队列实现
目录
编辑
1.栈
1.1 栈的概念和结构
1.2 栈的实现
1.2.1 初始化
1.2.2 销毁
1.2.3 入栈
1.2.4 出栈
1.2.5 获取栈顶元素
1.2.6 判空
1.2.7 获取数据个数
2.队列
2.1 队列的概念和结构
2.2 队列的实现
2.2.1 初始化
2.2.2 销毁
2.2.3 队尾入队列
2.2.4 队头出队列
2.2.5 获取队尾元素
2.2.6 获取队头元素
2.2.7 判空
2.2.8 获取数据个数
3.栈和队列面试题
3.1 括号匹配问题。OJ链接
3.2 用队列实现栈。OJ链接
3.3 用栈实现队列。OJ链接
3.4 设计循环队列。OJ链接
1.栈
1.1 栈的概念和结构
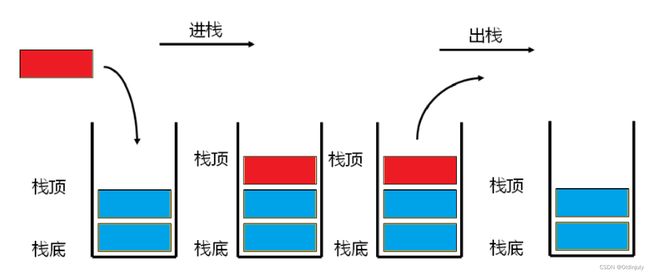
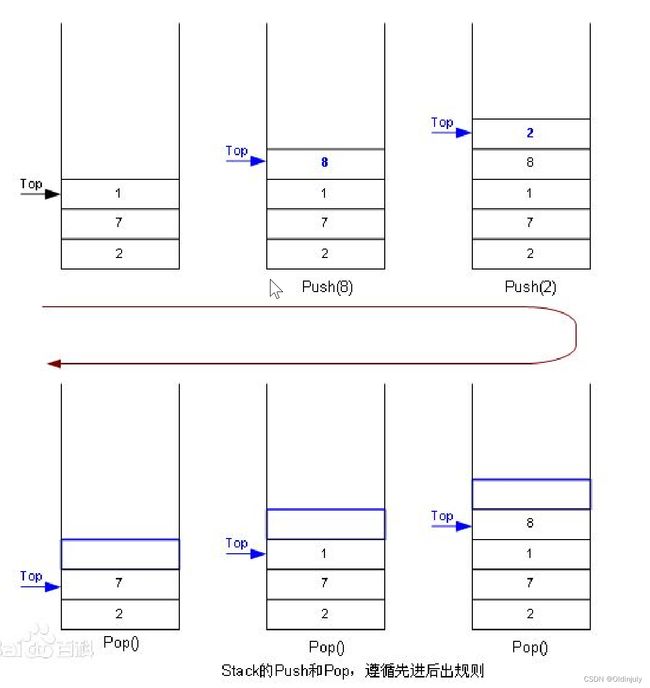
栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。
1.2 栈的实现
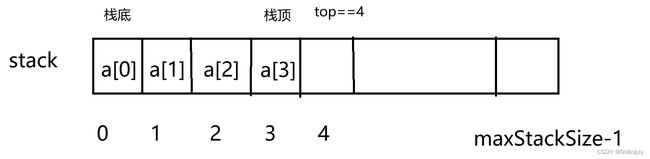
栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。
我们规定：top为栈顶元素的下一个位置的下标，也是栈中数据的个数。
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;//栈顶元素的下一个位置
int capacity;
}Stack;
void StackInit(Stack* pst);
void StackPush(Stack* pst, STDataType x);
void StackPop(Stack* pst);
STDataType StackTop(Stack* pst);
bool StackEmpty(Stack* pst);
int StackSize(Stack* pst);
void StackDestory(Stack* pst);
这里栈的接口实现和前面的顺序表相似。
1.2.1 初始化
void StackInit(Stack* pst)
{
assert(pst);
pst->a = NULL;
pst->top = 0;
pst->capacity = 0;
}
1.2.2 销毁
void StackDestory(Stack* pst)
{
assert(pst);
free(pst->a);
pst->a = NULL;
pst->capacity = 0;
pst->top = 0;
}
1.2.3 入栈
void StackPush(Stack* pst, STDataType x)
{
assert(pst);
if (pst->top == pst->capacity)
{
int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * newcapacity);
if (tmp == NULL)
{
perror("StackPush:");
exit(-1);
}
pst->a = tmp;
pst->capacity = newcapacity;
}
pst->a[pst->top] = x;
pst->top++;
}
1.2.4 出栈
void StackPop(Stack* pst)
{
assert(pst);
assert(pst->top > 0);
pst->top--;
}
1.2.5 获取栈顶元素
STDataType StackTop(Stack* pst)
{
assert(pst);
assert(pst->top > 0);
return pst->a[pst->top - 1];
}
1.2.6 判空
bool StackEmpty(Stack* pst)
{
assert(pst);
return pst->top == 0;
}
1.2.7 获取数据个数
int StackSize(Stack* pst)
{
assert(pst);
return pst->top;
}
2.队列
2.1 队列的概念和结构
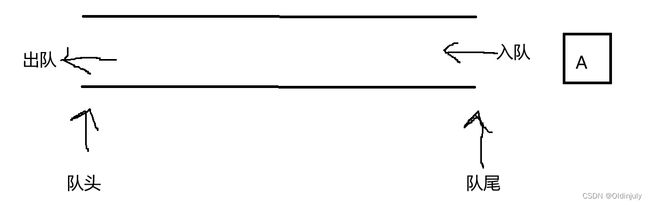
队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 的原则。
入队列：进行插入操作的一端称为队尾
出队列：进行删除操作的一端称为队头
简称：队尾入，对头出。
2.2 队列的实现
队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低。
那么链表使用单链表，还是带头双向循环链表呢？我们从两个方面来考虑：
双向循环：双向循环链表方便找尾，一定方便队列尾插，但是大可不必；我们可以设置一个尾结点变量QueueNode* tail来保存尾结点的值，也是可以使用单链表来解决的。
带头结点：队列的插入和删除是一定要修改头结点QueueNode* head或者尾结点QueueNode* tail的，所以我们函数参数可能要传二级指针，并且还要传两个值，会显得代码有些复杂；
- 此时有人会想到带头结点（哨兵位）的链表，带头结点时头删是不需要传二级了，但是插入改尾结点的问题没有得到解决，并且还是要传两个值。
- 那么增加返回值会解决吗？也是不可以的！第一次插入时head和tail都要修改，但是函数不能返回两个值；
- 此时我们可以再使用一种方法来解决二级指针问题：用结构体封装head和tail，通过该传结构体指针来修改head或者tail。
综上：我们可以进仅使用单链表就可以实现队列了，不需要双向循环链表。并且队列的结构体类型需要包含head头结点指针类型和tail尾结点指针类型。
typedef int QDataType;
typedef struct QueueNode
{
int data;
struct QueueNode* next;
}QueueNode;
typedef struct Queue
{
struct QueueNode* head;
struct QueueNode* tail;
int size;
}Queue;
补充：解决二级指针的三种办法：
- 带头结点（哨兵位）
- 函数带返回值
- 用结构体包起来（一般多个值可以用结构体包起来，一个值没有必要）。
2.2.1 初始化
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = NULL;
pq->tail = NULL;
pq->size = 0;
}
2.2.2 销毁
void QueueDestory(Queue* pq)
{
assert(pq);
QueueNode* cur = pq->head;
while (cur)
{
QueueNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
pq->size = 0;
}
2.2.3 队尾入队列
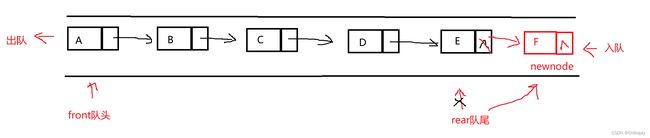入队，单链表尾部插入 
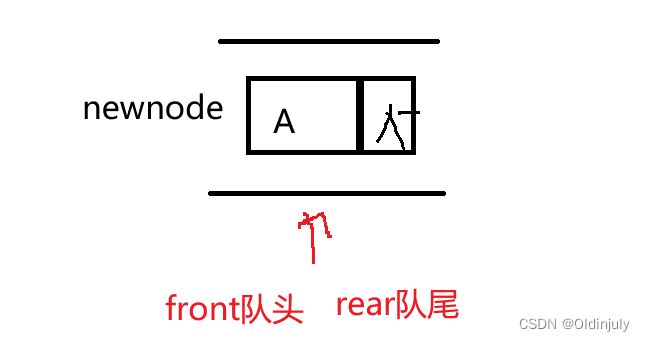空队列，第一次插入
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
if (newnode == NULL)
{
perror("QueueNode:");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
if (pq->tail == NULL)
{
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
pq->size++;
}2.2.4 队头出队列
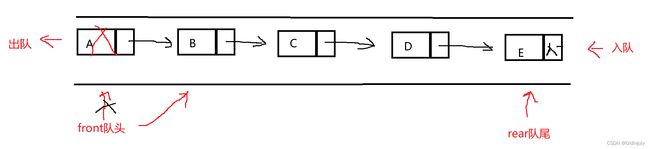出队，单链表头部删除 
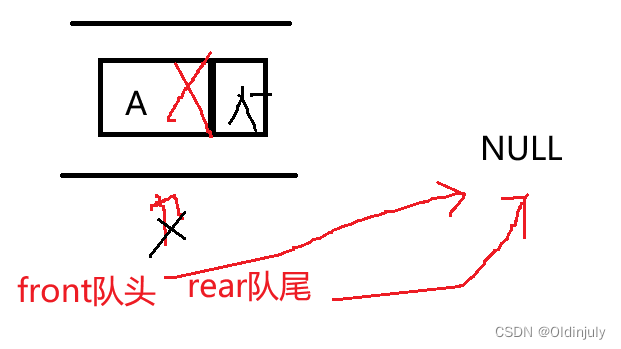删除最后一个元素
void QueuePop(Queue* pq)
{
assert(pq);
assert(pq->tail);
//错误写法：
//注意：删除做后一个时，pq->tail也是要置空的，但是这里并没有，tail变成了野指针
//QueueNode* newhead = pq->head->next;
//free(pq->head);
//pq->head = newhead;
//pq->size--;
//正确写法：
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QueueNode* newhead = pq->head->next;
free(pq->head);
pq->head = newhead;
}
pq->size--;
}注意：删除最后一个元素时，要给tail置空，否则tail是野指针。
2.2.5 获取队尾元素
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
2.2.6 获取队头元素
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
2.2.7 判空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->tail == NULL;
}
2.2.8 获取数据个数
int QueueSize(Queue* pq)
{
assert(pq);
return pq->size;
}
3.栈和队列面试题
3.1 括号匹配问题。OJ链接
描述：
分析：
- 遇到左括号（ { [，入栈；
- 遇到右括号 ）} ]，拿出栈顶元素和该有括号比较是否相匹配；
- 注意数量不匹配的特殊情况：右括号多循环退出时栈不为空，左括号多导致在循环中栈已经为空，二者都要判断。
代码（C++）：
class Solution {
public:
bool isValid(string s)
{
stack st;
int i = 0;
while(s[i])
{
if(s[i] == '(' || s[i] == '{' || s[i] == '[')
st.push(s[i]);
else
{
//数量不匹配：( { [ ] } ) )
if(st.empty())
return false;
//类型不匹配:( { [ } } )
char topVal = st.top();
if((topVal == '{' && s[i] != '}')
|| (topVal == '[' && s[i] != ']')
|| (topVal == '(' && s[i] != ')'))
return false;
st.pop();
}
i++;
}
//数量不匹配：( ( { [ ] } )
return st.empty();
}
};
3.2 用队列实现栈。OJ链接
描述：
分析：
写这种题首先要相当了解栈和队列两种数据结构的特性。栈是后进先出，队列是先进先出。
用两个队列实现一个栈，具体实现思路如下：
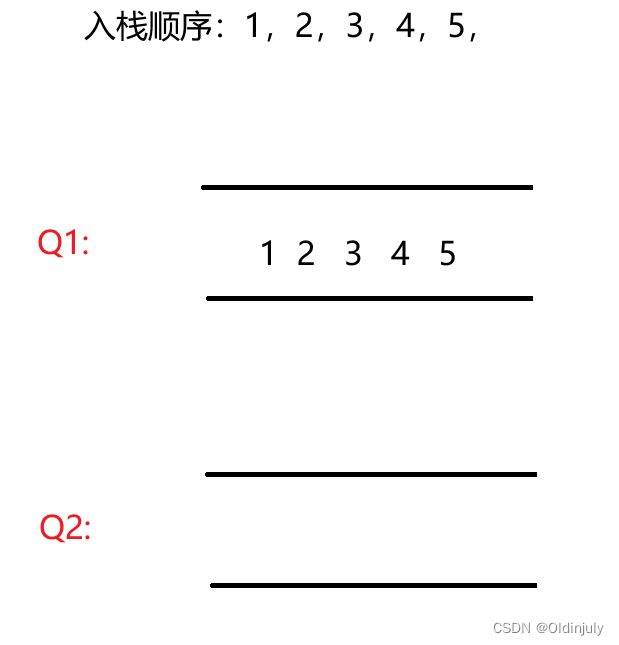
- 入栈直接入不为空的队列；一开始入栈时，两个队列均为空，随便入一个队列。
- 返回栈顶元素，即是返回队列的队尾元素。
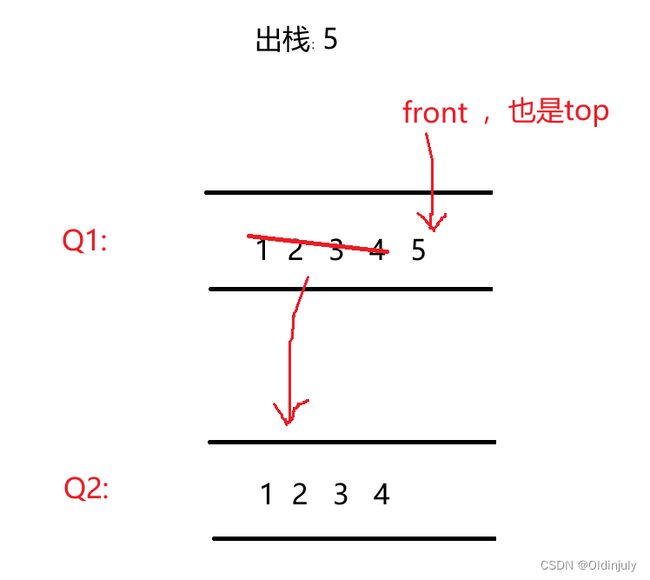
- 出栈时，遵循后进先出原则，最先出来的应该是5，那么如何出栈呢？
最先想到的应该是返回队尾元素，因为栈的栈顶元素正好对应队列的队尾元素，但是这样并不能删除栈顶元素，因为队列只支持删除队头元素。
- 既然给了我们两个队列，那么另一个队列也要利用上，我们可以把不为空队列中的前size-1个元素转移带空队列中，这样原队列只剩一个栈顶元素，也是队列的队头，直接pop删除队头即可。
- 判空：两个队列都为空，栈即为空。
- 综上：push即是插入到不为空的队列，pop即是转移队列元素。
代码实现：
C++：
class MyStack {
public:
MyStack()
{
}
void push(int x)
{
if(q1.empty())
q2.push(x);
else
q1.push(x);
}
int pop()
{
queue* emptyQ = &q1;
queue* popQ = &q2;
if(q2.empty())
{
emptyQ = &q2;
popQ = &q1;
}
while(popQ->size() != 1)
{
emptyQ->push(popQ->front());
popQ->pop();
}
int retVal = popQ->front();
popQ->pop();
return retVal;
}
int top()
{
if(q1.empty())
return q2.back();
else
return q1.back();
}
bool empty()
{
return q1.empty() && q2.empty();
}
private:
queue q1;
queue q2;
};
C语言：
typedef struct
{
Queue q1;
Queue q2;
} MyStack;
MyStack* myStackCreate()
{
MyStack* st = (MyStack*)malloc(sizeof(MyStack));
QueueInit(&st->q1);
QueueInit(&st->q2);
return st;
}
void myStackPush(MyStack* obj, int x)
{
if(!QueueEmpty(&obj->q1))
{
QueuePush(&obj->q1, x);
}
else
{
QueuePush(&obj->q2, x);
}
}
int myStackPop(MyStack* obj)
{
Queue* emptyQ = &obj->q1;
Queue* popQ = &obj->q2;
if(QueueEmpty(&obj->q2))
{
emptyQ = &obj->q2;
popQ = &obj->q1;
}
while(QueueSize(popQ) > 1)
{
QueuePush(emptyQ, QueueFront(popQ));
QueuePop(popQ);
}
int retVal = QueueFront(popQ);
QueuePop(popQ);
return retVal;
}
int myStackTop(MyStack* obj)
{
Queue* emptyQ = &obj->q1;
Queue* popQ = &obj->q2;
if(QueueEmpty(&obj->q2))
{
emptyQ = &obj->q2;
popQ = &obj->q1;
}
return QueueBack(popQ);
}
bool myStackEmpty(MyStack* obj)
{
return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}
void myStackFree(MyStack* obj)
{
QueueDestory(&obj->q1);
QueueDestory(&obj->q2);
free(obj);
}
3.3 用栈实现队列。OJ链接
描述：
分析：
此题也是对栈和队列特性的考察，队列是先进先出，栈是后进先出。
栈是后进先出，如果把栈颠倒过来就是先进先出了，而点颠倒过来利用两个栈很好实现。
两个栈实现队列，具体思路如下：
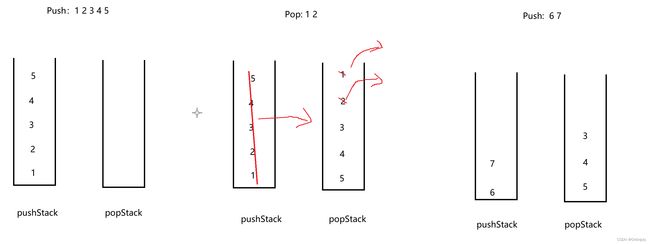
- 两个栈一个为插入栈pushStack，一个为删除栈popStack；
- 入队时元素压入pushStack；
- 出队时，如果popStack为空，pushStack中的元素颠倒至popStack，这样popStack出栈就和出队顺序一致。
注意：这题和上一题的思路有所不同，上一题所有元素要在两个队列之间来回导入，这题可以，但是没有必要。
代码实现：
typedef struct
{
Stack pushSt;
Stack popSt;
} MyQueue;
MyQueue* myQueueCreate()
{
MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
StackInit(&obj->pushSt);
StackInit(&obj->popSt);
return obj;
}
void myQueuePush(MyQueue* obj, int x)
{
StackPush(&obj->pushSt, x);
}
int myQueuePeek(MyQueue* obj)
{
if(StackEmpty(&obj->popSt))
{
while(!StackEmpty(&obj->pushSt))
{
StackPush(&obj->popSt, StackTop(&obj->pushSt));
StackPop(&obj->pushSt);
}
}
return StackTop(&obj->popSt);
}
int myQueuePop(MyQueue* obj)
{
int retVal = myQueuePeek(obj);
StackPop(&obj->popSt);
return retVal;
}
bool myQueueEmpty(MyQueue* obj)
{
return StackEmpty(&obj->pushSt) && StackEmpty(&obj->popSt);
}
void myQueueFree(MyQueue* obj)
{
StackDestory(&obj->pushSt);
StackDestory(&obj->popSt);
free(obj);
}
3.4 设计循环队列。OJ链接
描述：
分析：
循环队列可以用循环链表和数组来实现，这题队列的长度是固定的，并不适合使用链表来实现；如果使用链表，需要提前使用循环多次malloc。所以这题我们使用数组实现会更加方便。
用数组实现，我们要注意一下几点：
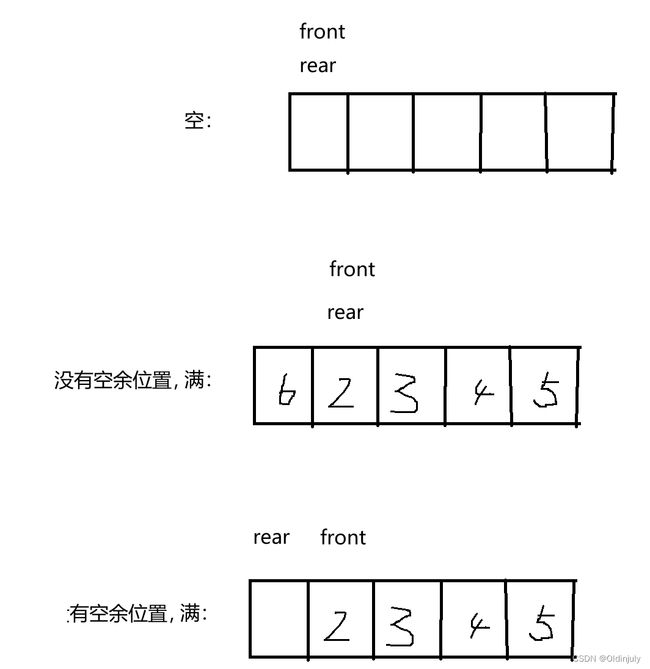
- 数组元素区间左闭右开：[front,rear)，即rear是队尾元素下一个位置的下标；如果rear是队尾元素的下标，队列为空和队列只有一个元素时，都是front==rear，会产生冲突。
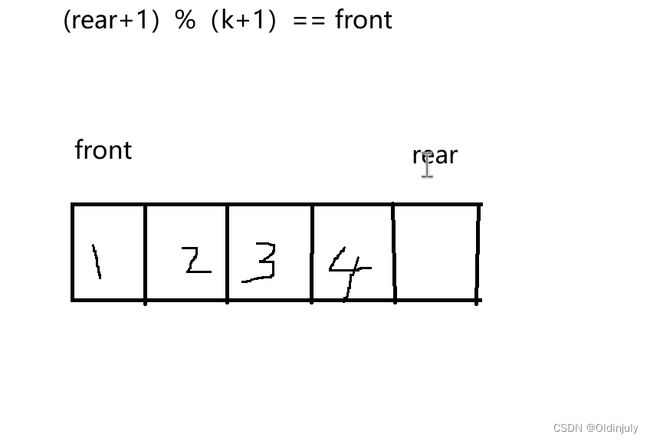
- 数组要多开一个空间来解决假溢出问题（即空和满冲突）：没有这个多余空间，空和满的条件都是front == rear，产生冲突。有了这个空间，空的条件是front == rear，满的条件是rear+1 == front。所以数组的数据个数是k，数组大小是k+1。
- 数组为了实现循环，我们要进行取模来保证front和rear能回到数组起始位置。
push：rear = (rear+1)%(k+1)
pop：front = (front+1)%(k+1)
判满：(rear+1)%(k+1) == front
取队尾：a[(rear+k)%(k+1)]
总结：
判空：rear == front
判满：(rear+1)%(k+1) == front
push: rear = (rear + 1)%(k + 1)
pop: front = (front + 1)%(k + 1)
取队头：a[front]
取队尾：a[(rear + k)%(k + 1)]
代码实现：
typedef struct
{
int* a;
int front;
int rear;
int k;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k)
{
MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
obj->a = (int*)malloc(sizeof(int) * (k + 1));
obj->k = k;
obj->front = obj->rear = 0;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj)
{
return obj->front == obj->rear;
}
bool myCircularQueueIsFull(MyCircularQueue* obj)
{
//数据个数k，数组大小k+1
return (obj->rear + 1) % (obj->k + 1) == obj->front;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value)
{
if(myCircularQueueIsFull(obj))
return false;
obj->a[obj->rear] = value;
obj->rear = (obj->rear + 1) % (obj->k + 1);
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj)
{
if(myCircularQueueIsEmpty(obj))
return false;
obj->front = (obj->front + 1) % (obj->k + 1);
return true;
}
int myCircularQueueFront(MyCircularQueue* obj)
{
if(myCircularQueueIsEmpty(obj))
return -1;
else
return obj->a[obj->front];
}
int myCircularQueueRear(MyCircularQueue* obj)
{
if(myCircularQueueIsEmpty(obj))
return -1;
else
return obj->a[(obj->rear + obj->k) % (obj->k + 1)];
}
void myCircularQueueFree(MyCircularQueue* obj)
{
free(obj->a);
obj->front = obj->rear = 0;
free(obj);
}