机器学习技术（七）——有监督学习之逻辑回归算法原理及实操

机器学习技术（七）——有监督学习之逻辑回归算法原理及实操

一、引言

当你想要解决一个分类问题时，逻辑回归是一种常用且强大的统计分析工具。它能够根据一系列特征值来预测一个样本属于某一类的概率。 逻辑回归的灵活性、易解释性和计算效率使其成为了数据科学领域的重要技术之一。

本文内容：详细介绍逻辑回归算法原理，基于python的逻辑回归的底层代码实现及调用。基于逻辑回归的模型探索被调查人员年龄，估计工资以及是否会购买某产品的关系，并将预测结果进行可视化。

二、逻辑回归算法原理

1、我们定义逻辑回归的预测函数为
$$h_{\theta }(x)=g({\theta }^{T}x)$$
其中g(x)为sigmoid函数
$$g(x)=\frac{1}{1+e^{-x}}$$
对于二分类任务有“单位阶跃函数”用来将实值z转换为0或1
$$y=\{\begin{array}{ll}0,& z<0\\ 0.5,& z=0\\ 1,& z>0\end{array}$$
最后我们可以得到下方函数，0.5可以作为分类的边界
$$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}X}}$$

几种决策边界的例子：

关于逻辑回归的代价函数，设代价函数为：
$$Cost(h_{\theta }(x),y)=\{\begin{array}{ll}-log(h_{\theta }(x))& ify=1\\ -log(1-h(1-h_{\theta }(x)))& ify=0\end{array}$$
由上式可以推出：
$$Cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))-(1-y)log(1-h_{\theta }(x))$$
则在逻辑回归模型使用梯度下降算法中的代价函数可以表示为：
$$J(\theta )=-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$$

三、实践案例介绍

1、数据集及需求

本案例使用的数据样本为400用户的基本信息，其中包含每个样本的ID，性别，年龄，估计工资以及是否购买该产品。其中我们选择的自变量为用户的年龄，估计工资。应变量为是否购买该产品，并以0表示不否买，1表示购买该产品。

User ID	Gender	Age	EstimatedSalary	Purchased
15624510	Male	19	19000	0
15810944	Male	35	20000	0
15668575	Female	26	43000	0
15603246	Female	27	57000	0
15804002	Male	19	76000	0
15728773	Male	27	58000	0
15598044	Female	27	84000	0
15694829	Female	32	150000	1
15600575	Male	25	33000	0

数据集地址：https://download.csdn.net/download/tianhai12/88275733

采用逻辑回归模型通过对400名用户的年龄以及估计工资对是否购买该产品进行预测，并对数据样本的训练集以及测试集分别进行模型预测结果的可视化来显示模型表现。

2、导入相关依赖库

讲数据处理所需库以及可视化依赖包导入。

#导入相关依赖包
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

3、读取并查看数据

将400名用户数据导入，并将其中年龄和估计工资数据命名为x，将是否购买该产品设置为y。

输入：

#导入数据集
dataset = pd.read_csv('ml/Social_Network_Ads.csv')
#提取所有的行，索引为2,3的列
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values

#查看前五行数据集
dataset.head()

结果显示如下，每位用户共有五组特征，其中我们主要关注年龄，估计工资以及是否购买该产品。

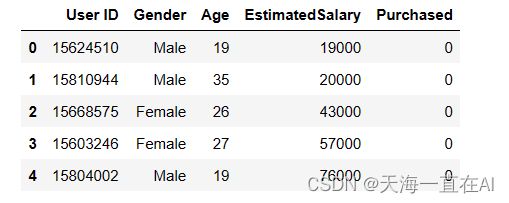
4、数据预处理

将我们所需数据 按3：1的比例划分为训练集以及测试集以便后续训练模型，并对所有原始数据进行标准化为均值为0方差为1的数据以防止预测结果被一些维度较大的值影响。

#导入划分数据集的方法
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
#数据标准化
#导入标准化方法
from sklearn.preprocessing import StandardScaler
#标准化数据，保证每个维度的特征数据方差为1，均值为0。使得预测结果不会被某些维度过大的特征值而主导
sc = StandardScaler()
#将标准化的数据进行重定义
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

划分数据集为训练集和测试集，test_size参数表示测试集占总数据集的比例，这里的random_state就是为了保证程序每次运行都分割一样的训练集合测试集。否则，同样的算法模型在不同的训练集和测试集上的效果不一样。当你用sklearn分割完测试集和训练集，确定模型和促初始参数以后，你会发现程序每运行一次，都会得到不同的准确率，无法调参。这个时候就是因为没有加random_state。加上以后就可以调参了。

5、构建模型

导入逻辑回归模型，并基于上述所得训练集训练模型。

输入：

#使用训练数据集来训练模型
#导入逻辑回归模型
from sklearn.linear_model import LogisticRegression
#初始化逻辑回归分类器
classifier = LogisticRegression(solver='liblinear',random_state = 0)
#调用LogisticRegression中的fit函数/模块用来训练模型参数
classifier.fit(X_train, y_train)

solver的选项：['liblinear', 'newton-cg', 'lbfgs', 'sag', 'saga']

输出模型如下,其中各个参数所代表含义如下：

(可能根据包的版本不同,详细参数也有所不同,这里简单例举，具体可以参考自己电脑中LogisticRegression方法内的介绍)

LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class=‘warn’,
n_jobs=None, penalty=‘l2’, random_state=0, solver=‘warn’,
tol=0.0001, verbose=0, warm_start=False)
以下为逻辑回归模型各个函数意义：
penalty：惩罚项，str类型，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。
dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。
c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。
fit_intercept：是否存在截距或偏差，bool类型，默认为True。
intercept_scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。
class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者’balanced’字符串，默认为不输入，也就是不考虑权重，即为None。
random_state：随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。
solver：优化算法选择参数，只有五个可选参数，即’liblinear’, ‘newton-cg’, ‘lbfgs’, ‘sag’, ‘saga’。默认为liblinear。solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择，分别是：
liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。
saga：线性收敛的随机优化算法的的变重。

6、测试模型

导入所需方法，并测试模型。

输入：

#使用训练好的模型对X_test进行预测，结果存储在变量y_pred中
y_pred = classifier.predict(X_test)
#构建混淆矩阵
#导入构建混淆矩阵的方法
from sklearn.metrics import confusion_matrix
#分别传入测试集的真实值和预测值来构建混淆矩阵， y_test是样本真实结果，y_pred是样本预测结果
cm = confusion_matrix(y_test, y_pred)
print(cm)
#使用逻辑回归模型自带的评分函数score获得模型在测试集上的准确性结果
print('Accuracy of LR Classifier:',classifier.score(X_test,y_test))

输出结果为混淆矩阵以及模型预测准确率。由结果可知，测试集中100样本预测对了89个，模型预测准确率为0.89.

输出：

[[65  3]
 [ 8 24]]
Accuracy of LR Classifier: 0.89

7、可视化模型

步骤1 训练集结果及可视化

导入可视化方法，首先对训练集预测数据以及模型预测结果进行可视化。

输入：

#可视化训练数据集的结果
#导入可视化的方法
from matplotlib.colors import ListedColormap
#训练集重新赋值
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                    np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))

#输出X1，X2结果
print(X1,X2)
#以红色表示不购买该产品，绿色代表购买该产品
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
            alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
   plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
               c = ListedColormap(('red', 'green'))(i), label = j)
#添加图表的描述
plt.title('Logistic Regression (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

输出为X1，X2结果以及模型预测与真实值比较可视化图。

[[-2.99318916 -2.98318916 -2.97318916 ...  3.13681084  3.14681084
   3.15681084]
 [-2.99318916 -2.98318916 -2.97318916 ...  3.13681084  3.14681084
   3.15681084]
 [-2.99318916 -2.98318916 -2.97318916 ...  3.13681084  3.14681084
   3.15681084]
 ...
 [-2.99318916 -2.98318916 -2.97318916 ...  3.13681084  3.14681084
   3.15681084]
 [-2.99318916 -2.98318916 -2.97318916 ...  3.13681084  3.14681084
   3.15681084]
 [-2.99318916 -2.98318916 -2.97318916 ...  3.13681084  3.14681084
   3.15681084]] [[-2.58254245 -2.58254245 -2.58254245 ... -2.58254245 -2.58254245
  -2.58254245]
 [-2.57254245 -2.57254245 -2.57254245 ... -2.57254245 -2.57254245
  -2.57254245]
 [-2.56254245 -2.56254245 -2.56254245 ... -2.56254245 -2.56254245
  -2.56254245]
 ...
 [ 3.30745755  3.30745755  3.30745755 ...  3.30745755  3.30745755
   3.30745755]
 [ 3.31745755  3.31745755  3.31745755 ...  3.31745755  3.31745755
   3.31745755]
 [ 3.32745755  3.32745755  3.32745755 ...  3.32745755  3.32745755
   3.32745755]]

该散点图中红色代表不购买该产品，绿色代表购买该产品。由图可知训练集中300个样本大部分被分对了，小部分红点在绿色部分，绿点在红色部分，为没有预测对的点，由图可知，该模型在训练集上表现连良好。

步骤2 测试集结果及可视化

对测试集数据进行相同可视化方法。

输入：

#可视化测试集结果，步骤与训练集相似。
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                    np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
            alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
   plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
               c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Logistic Regression (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

测试机输出结果如下所示，我们可以发现共有三个红点被错分在绿色区域，8个绿点被错分在红色区域，与混淆矩阵结果一致，总共11个样本预测错误，模型准确率0.89，表现良好。

四、总结

通过基于逻辑回归探索400名用户的年龄以及估计工资对是否购买该产品进行预测，并对数据样本的训练集以及测试集分别进行模型预测结果的可视化来显示模型表现。由可视化图像可得模型表现良好，后续可以通过用户年龄以及估计工资来预测他是否会购买该产品，进行一个目标客户选择。