机器学习技术(九)——支持向量机算法实操(基于SVM的模型对潜在运营商客户进行分类)
机器学习技术(九)——支持向量机算法实操
文章目录
- 机器学习技术(九)——支持向量机算法实操
-
- 一、引言
- 二、数据集介绍
- 三、导入相关依赖库
- 四、读取数据
- 五、数据可视化分析
-
- 1、是否为潜在客户与不同用户主叫时长对比
- 2、是否为潜在合约客户与被叫时长对比
- 3、是否为潜在合约用户与业务类型对比
- 4、是否为潜在合约用户与主叫时长以及免费流量使用情况对比
- 六、数据预处理
-
- 1、划分数据
- 步骤2 类别特征编码
- 3、数据归一化
- 七、 训练SVM模型
-
- 1、训练简单模型:SVM
- 2、训练核函数=rbf的SVM算法:调参
- 3、使用最优超参再次进行训练
- 八、模型评估
- 九、总结
一、引言
本文主要包含基于python的SVM的代码实现及调用。基于SVM的模型探索该运营商用户业务类型以及每月使用数据来区分是否为给运营商潜在合约用户。
二、数据集介绍
数据样本为10000名用户的手机业务使用信息,其中包含每个样本的ID,业务类型,主叫时长,被叫时长,免费流量,几万消费,月均上网时长,入网时长,最近一次消费金额,总缴费金额,缴费次数,余额以及是否为潜在合约客户共13个特征。其中我们选择的自变量为除用户ID以外的11个特征。应变量为是否为潜在合约用户,并以0表示不是潜在合约客户,1表示是潜在合约客户。
数据集:https://download.csdn.net/download/tianhai12/88275733
以下为原始数据的字段信息,后续将会以说明作为特征名。
| 名称 | 说明 | 类型 | 备注 |
|---|---|---|---|
| user_id | 用户标识 | int | |
| service_kind | 业务类型 | string | 2G\3G\4G |
| call_duration | 主叫时长(分) | ||
| called_duration | 被叫时长(分) | ||
| in_package_flux | 免费流量 | ||
| out_package_flux | 计费流量 | ||
| 月均上网时长(分) | |||
| net_duration | 入网时长(天) | long | |
| last_recharge_value | 最近一次缴费金额(元) | ||
| total_recharge_value | 总缴费金额(元) | ||
| total_recharge_count | 缴费次数 | ||
| contractuser_flag | 是否潜在合约用户 | ||
| silent_serv_flag | 是否三无用户 | int | 0:否, 1:是, 三无:无月租费,无最低消费,无来电显示 |
| pay_type | 付费类型 | int | 0:预付费, 1:后付费 |
三、导入相关依赖库
将所需与处理数据,所需模型以及可视化依赖包导入。
#导入基础数据处理以及数据可视化依赖包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import datasets
#导入构建模型所需包
from sklearn import svm,metrics
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV,RandomizedSearchCV
from sklearn.preprocessing import OneHotEncoder
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
四、读取数据
将10000名用户数据导入,并将其中年龄和估计工资数据命名为x,将是否购买该产品设置为y。
输入:
data= pd.read_csv('./ml/data_carrier_svm.csv',encoding ='utf8')
#查看前五行数据集
data.head()
前五位用户结果显示如下,每位用户共有13组特征,其中我们主要关注除用户标识外其他特征。

五、数据可视化分析
1、是否为潜在客户与不同用户主叫时长对比
#不同用户的主叫时长分布情况对比
cond = data['是否潜在合约用户']==1
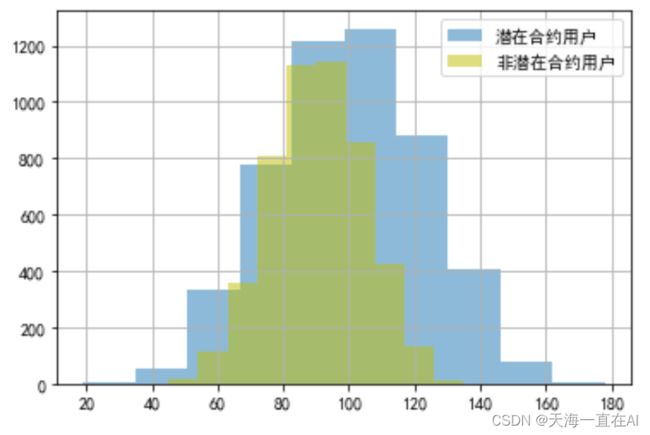
data[cond]['主叫时长(分)'].hist(alpha =0.5,label='potential_contract_user(潜在合约用户)')
data[~cond]['主叫时长(分)'].hist(color='y',alpha = 0.5,label='no_potential_contract_user(非潜在合约用户)')
plt.legend()
由图可得在主叫时长超过80分钟的用户中目前在合约用户明显要多于费钱在合约用户,且主叫时长在100分钟至120分钟的潜在用户人数最多。
2、是否为潜在合约客户与被叫时长对比
#不同用户的被叫时长分布情况对比
cond = data['是否潜在合约用户']==1
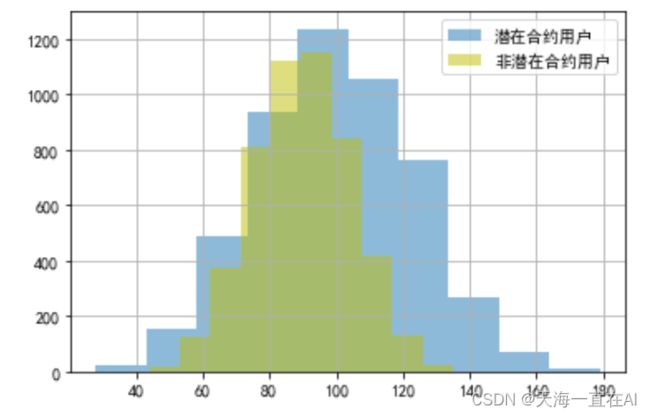
data[cond]['被叫时长(分)'].hist(alpha =0.5,label='潜在合约用户')
data[~cond]['被叫时长(分)'].hist(color='y',alpha = 0.5,label='非潜在合约用户')
plt.legend()
输出结果如下所示,潜在客户和非潜在客户人数都在被叫时长为100分钟左右到达峰值,随后慢慢下降。
3、是否为潜在合约用户与业务类型对比
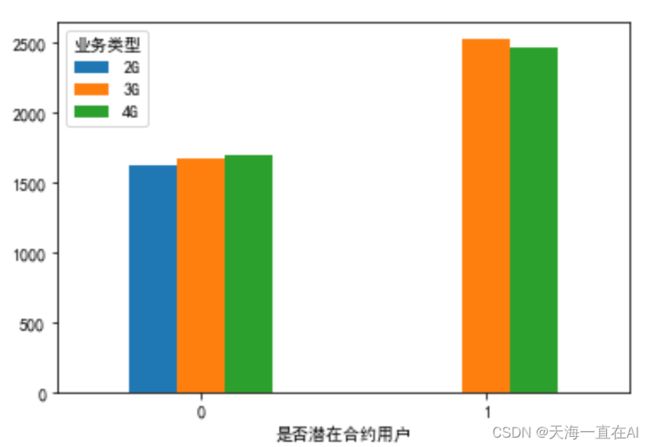
探索是否为潜在合约用户与业务类型之间关系。
#不同用户的业务类型情况对比
grouped =data.groupby(['是否潜在合约用户','业务类型'])['用户标识'].count().unstack()
grouped.plot(kind= 'bar',alpha =1.0,rot = 0)
输出结果如下所示,可以看出潜在合约客户并没有使用2G业务的,而使用3G,4G业务人数相差不多。反观非潜在用户,使用2G,3G,4G业务用户人数差不多。
#统计两类用户具体人数。
data['是否潜在合约用户'].value_counts()
得到
1 5003
0 4997
Name: 是否潜在合约用户, dtype: int64
4、是否为潜在合约用户与主叫时长以及免费流量使用情况对比
将是否为潜在合约用户与主叫时长以及免费流量使用情况分布情况进行数据可视化。
输入:
#生成数据可视化
y = data.loc[:,'是否潜在合约用户']
plt.scatter(data.loc[:,'主叫时长(分)'],data.loc[:,'免费流量'],c=y,alpha=0.5)
结果如下,其中X轴表示主叫时长(分),Y轴表示免费流量,黄点代表潜在合约客户,紫点表示非潜在合约客户,由图可得,两者虽然区分较为明显,但有少量区域重合。

六、数据预处理
1、划分数据
首先将自变量(除用户标识外11个特征)与应变量(是否为潜在合约客户)划分并定义。
#分割特征数据集和便签数据集
X = data.loc[:,'业务类型':'余额']
y= data.loc[:,'是否潜在合约用户']
print('The shape of X is {0}'.format(X.shape))
print('The shape of y is {0}'.format(y.shape))
输出结果为X,Y结构如下。
The shape of X is (10000, 11)
The shape of y is (10000,)
步骤2 类别特征编码
因为业务类别三类为字符形式,为后续数据分析及建模,将其用One-hot编码。
# 使用One-hot编码
service_df = pd.get_dummies(X['业务类型'])
X_enc = pd.concat([X,service_df],axis = 1).drop('业务类型',axis=1)
X_enc.head()
3、数据归一化
因各个特征维度相差较大,训练之前先进行归一化处理
#导入方法
from sklearn.preprocessing import normalize
X_normalized = normalize(X_enc)
#分割训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X_normalized,y,test_size = 0.2, random_state=112)
print('The shape of X_train is {0}'.format(X_train.shape))
print('The shape of X_test is {0}'.format(X_test.shape))
训练集与测试集比例为4:1.
输出:
The shape of X_train is (8000, 13)
The shape of X_test is (2000, 13)
将归一化后训练集数据进行可视化。
#生成数据可视化
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)
七、 训练SVM模型
1、训练简单模型:SVM
#模型实例化
linear_clf = svm.LinearSVC()
#在训练集上训练模型
linear_clf.fit(X_train,y_train)
#在测试集上预测
y_pred = linear_clf.predict(X_test)
#计算准备;率
score = metrics.accuracy_score(y_test,y_pred)
print('The accuracy score of the model is: {0}'.format(score))
#查看混淆举证
metrics.confusion_matrix(y_test,y_pred)
输出结果为测试集混淆矩阵以及模型预测准确率。由结果可知,测试集中2000样本预测对了1728个,模型预测准确率为0.864.
The accuracy score of the model is: 0.864
array([[935, 103],
[169, 793]], dtype=int64)
2、训练核函数=rbf的SVM算法:调参
训练参数得到最优解。
# 设置调试参数的范围
C_range = np.logspace(-5,5,5)
gamma_range = np.logspace(-9,2,10)
clf = svm.SVC(kernel='rbf',cache_size=1000,random_state=117)
param_grid = {'C':C_range,
'gamma':gamma_range}
# GridSearch作用在训练集上
grid = GridSearchCV(clf,param_grid=param_grid,scoring= 'accuracy',n_jobs=2,cv =5)
grid.fit(X_train,y_train)
通过交叉检验寻找最优参数,其中参数解释如下,这里给出的定义仅供参考,具体看你电脑上包的版本。
#estimator:所使用的分类器,或者pipeline
#param_grid:值为字典或者列表,即需要最优化的参数的取值
#scoring:准确度评价标准,默认None,这时需要使用score函数;或者如scoring='roc_auc',根据所选模型不同,评价准则不同。字符串(函数名),或是可调用对象,需要其函数签名形如:scorer(estimator, X, y);如果是None,则使用estimator的误差估计函数。
#n_jobs:并行数,int:个数,-1:跟CPU核数一致, 1:默认值。
#pre_dispatch:指定总共分发的并行任务数。当n_jobs大于1时,数据将在每个运行点进行复制,这可能导致OOM,而设置pre_dispatch参数,则可以预先划分总共的job数量,使数据最多被复制pre_dispatch次
#iid:默认True,为True时,默认为各个样本fold概率分布一致,误差估计为所有样本之和,而非各个fold的平均。
#cv:交叉验证参数,默认None,使用三折交叉验证。指定fold数量,默认为3,也可以是yield训练/测试数据的生成器。
#refit:默认为True,程序将会以交叉验证训练集得到的最佳参数,重新对所有可用的训练集与开发集进行,作为最终用于性能评估的最佳模型参数。即在搜索参数结束后,用最佳参数结果再次fit一遍全部数据集。
#verbose:日志冗长度,int:冗长度,0:不输出训练过程,1:偶尔输出,>1:对每个子模型都输出。
Attributes:
#best_estimator_:效果最好的分类器
#best_score_:成员提供优化过程期间观察到的最好的评分
#best_params_:描述了已取得最佳结果的参数的组合
#best_index_:对应于最佳候选参数设置的索引(cv_results_数组的索引)。
#Methods:
#decision_function:使用找到的参数最好的分类器调用decision_function。
#fit(X, y=None, groups=None, **fit_params):训练
#get_params(deep=True):获取这个估计器的参数。
#predict(X):用找到的最佳参数调用预估器。(直接预测每个样本属于哪一个类别)
#predict_log_proda(X):用找到的最佳参数调用预估器。(得到每个测试集样本在每一个类别的得分取log情况)
#predict_proba(X):用找到的最佳参数调用预估器。(得到每个测试集样本在每一个类别的得分情况)
#score(X, y=None):返回给定数据上的得分,如果预估器已经选出最优的分类器。
#transform(X):调用最优分类器进行对X的转换。
注意:会跑一段时间,看电脑配置
GridSearchCV(cv=5, estimator=SVC(cache_size=1000, random_state=117), n_jobs=2,
param_grid={'C': array([1.00000000e-05, 3.16227766e-03, 1.00000000e+00, 3.16227766e+02,
1.00000000e+05]),
'gamma': array([1.00000000e-09, 1.66810054e-08, 2.78255940e-07, 4.64158883e-06,
7.74263683e-05, 1.29154967e-03, 2.15443469e-02, 3.59381366e-01,
5.99484250e+00, 1.00000000e+02])},
scoring='accuracy')
输出最优参数得到最优模型。
# 获得最佳model
print(grid.best_score_)
print(grid.best_params_)
print(grid.best_estimator_)
有输出结果可知,最优c=100000,gamma=5.994842503189421
输出:
0.966625
{'C': 100000.0, 'gamma': 5.994842503189421}
SVC(C=100000.0, cache_size=1000, gamma=5.994842503189421, random_state=117)
3、使用最优超参再次进行训练
有上述训练所得参数构建模型,并在训练数据上训练以及测试数据集上进行测试。
也需要跑一会儿
# 建立最好参数示例
clf_best = svm.SVC(kernel="rbf",C=grid.best_params_['C'],
gamma = grid.best_params_['gamma'],probability=True)
# 使用训练数据训练
clf_best.fit(X_train,y_train)
# 使用测试数据测试
y2_pred = clf_best.predict(X_test)
看一下测试数据结构
y2_pred
array([0, 1, 0, ..., 1, 1, 1], dtype=int64)
八、模型评估
# 计算测试集准确率
accuracy = metrics.accuracy_score(y_test,y2_pred)
print("The accuracy is %f"%accuracy)
# 显示混淆矩阵
metrics.confusion_matrix(y_test,y2_pred)
输出结果为混淆矩阵以及准确率,可以发现准确率为0.968比之前简单模型准确率0.864高很多。
The accuracy is 0.968000
array([[1019, 19],
[ 45, 917]], dtype=int64)
通过上述所得混淆矩阵生成ROC曲线
# 获取类别1的预测概率分布的分数
y2_pred_prob = clf_best.predict_proba(X_test)[:, 1]
# 获取ROC曲线
fpr, tpr, thresholds = metrics.roc_curve(y_test, y2_pred_prob)
plt.plot(fpr, tpr)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.title('ROC curve for diabetes classifier')
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Sensitivity)')
plt.grid(True)
ROC曲线越陡,模型表现越好,由下ROC曲线曲线可得模型表现良好。

九、总结
通过SVM模型基于10000名用户的每月运营商业务业务使用情况对是否为该运营商潜在客户进行分类以及预测,实验当中对数据进行可视化来体现数据结构,并通过训练集构建经过调参后SVM模型来预测测试集数据,并以ROC图像显示分类效果。与其他实验不一样的地方,此处实验先训练简单模型,并得出预测准确率大约在0.864,再通过调参优化模型将模型预测准确率提升至0.968,表现良好!