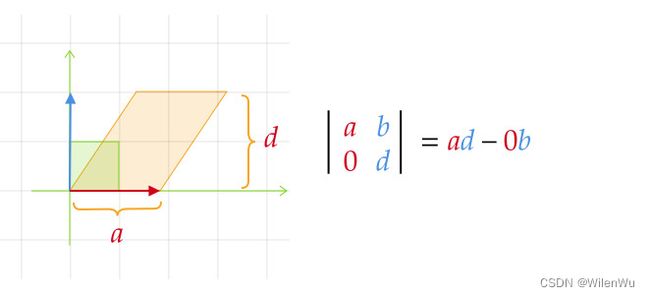线性代数的本质(四)——行列式

行列式

二阶行列式

行列式引自对线性方程组的求解。考虑两个方程的二元线性方程组
$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2=b_1\\ a_{21}{x}_1+a_{22}{x}_2=b_2\end{array}$$
可使用消元法，得
$$\begin{gathered} (a_{11}{a}_{22}-a_{12}{a}_{21})x_1=b_1{a}_{22}-a_{12}{b}_2 \\ (a_{11}{a}_{22}-a_{12}{a}_{21})x_2=a_{11}{b}_2-b_1{a}_{21} \end{gathered}$$
当 $a_{11}{a}_{22}-a_{12}{a}_{21}\ne 0$ 时，得
$$x_1=\frac{b_1{a}_{22}-a_{12}{b}_2}{a_{11}{a}_{22}-a_{12}{a}_{21}},x_2=\frac{a_{11}{b}_2-b_1{a}_{21}}{a_{11}{a}_{22}-a_{12}{a}_{21}}$$
从方程组解来看，分母 $a_{11}{a}_{22}-a_{12}{a}_{21}$ 是系数矩阵 $A=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]$ 的元素计算得到，称这个值为矩阵 $A$ 的二阶行列式(determinant)，记为 $\det A$ 或 $|A|$ ，或记为数表形式
∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21} ​a11​a21​​a12​a22​​ ​=a11​a22​−a12​a21​
利用二阶行列式的概念，分子也可写为二阶行列式
det ⁡ A 1 = ∣ b 1 a 12 b 2 a 22 ∣ = b 1 a 22 − a 12 b 2 det ⁡ A 2 = ∣ a 11 b 1 a 21 b 2 ∣ = a 11 b 2 − b 1 a 21 \det A_1=\begin{vmatrix} b_1 & a_{12} \\ b_2 & a_{22}\end{vmatrix}=b_1a_{22}-a_{12}b_2 \\ \det A_2=\begin{vmatrix} a_{11} & b_1 \\ a_{21} & b_2\end{vmatrix}=a_{11}b_2-b_1a_{21} detA1​= ​b1​b2​​a12​a22​​ ​=b1​a22​−a12​b2​detA2​= ​a11​a21​​b1​b2​​ ​=a11​b2​−b1​a21​
从上面对比可以看出，$x_j$ 的矩阵 $A_j$ 是系数矩阵 $A$的第 $j$ 列用常数项代替后的矩阵。这样，方程组的解可表示为
$$x_1=\frac{\det A_1}{\det A},x_2=\frac{\det A_2}{\det A}$$

$n$ 阶行列式

考虑三个方程的三元线性方程组，系数矩阵为
A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] A=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{bmatrix} A= ​a11​a21​a31​​a12​a22​a32​​a13​a23​a33​​ ​
用消元法可知未知数的分母同样是系数矩阵$A$ 的元素运算得到，于是定义三阶行列式为
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 11 a 23 a 32 − a 12 a 21 a 33 − a 13 a 22 a 31 \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{vmatrix} =a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32} -a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31} ​a11​a21​a31​​a12​a22​a32​​a13​a23​a33​​ ​=a11​a22​a33​+a12​a23​a31​+a13​a21​a32​−a11​a23​a32​−a12​a21​a33​−a13​a22​a31​
由二阶行列式的定义，上式可变为
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 ∣ a 22 a 23 a 32 a 33 ∣ − a 12 ∣ a 21 a 23 a 31 a 33 ∣ + a 13 ∣ a 11 a 12 a 21 a 22 ∣ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{vmatrix}= a_{11}\begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33}\end{vmatrix}- a_{12}\begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33}\end{vmatrix}+ a_{13}\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{vmatrix} ​a11​a21​a31​​a12​a22​a32​​a13​a23​a33​​ ​=a11​ ​a22​a32​​a23​a33​​ ​−a12​ ​a21​a31​​a23​a33​​ ​+a13​ ​a11​a21​​a12​a22​​ ​
进一步探索 $n$ 元线性方程组，可知高阶行列式定义。为书写方便，把元素 $a_{ij}$ 所在的行和列划掉后，剩下的元素组成的行列式称为 $a_{ij}$ 的余子式(cofactor)，记作 $M_{ij}$ ，并称
$$A_{ij}=(-1{)}^{i+j}{M}_{ij}$$
为 $a_{ij}$ 的代数余子式(algebraic cofactor)。

定义：方阵 $A$ 的行列式用第一行元素的代数余子式定义为
det ⁡ A = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ = ∑ j = 1 n a 1 j A 1 j \det A=\begin{vmatrix} a_{11}&a_{12}&\cdots&a_{1n} \\ a_{21}&a_{22}&\cdots&a_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{n1}&a_{n2}&\cdots&a_{nn} \\ \end{vmatrix}=\sum_{j=1}^na_{1j}A_{1j} detA= ​a11​a21​⋮an1​​a12​a22​⋮an2​​⋯⋯⋱⋯​a1n​a2n​⋮ann​​ ​=j=1∑n​a1j​A1j​
由定义易知，行列式可以按任意行(列)展开。
$$\begin{gathered} \det A=\sum _{j=1}^n{a}_{ij}{A}_{ij},\text{by row }i \\ \det A=\sum _{i=1}^n{a}_{ij}{A}_{ij},\text{by col }j \end{gathered}$$

行列式的性质

性质：使用数学归纳法可知

1. 行列式与其转置行列式相等：$\det A^T=\det A$
2. 互换行列式两行(列)，行列式改变符号。
   ∣ a b c d ∣ = − ∣ c d a b ∣ \begin{vmatrix}a&b\\c&d\end{vmatrix}=-\begin{vmatrix}c&d\\a&b\end{vmatrix} ​ac​bd​ ​=− ​ca​db​ ​
3. 行列式的某一行(列)所有元素同乘以数$k$，等于数$k$乘以该行列式。
   ∣ k a b k c d ∣ = k ∣ a b c d ∣ \begin{vmatrix}ka&b\\kc&d\end{vmatrix}=k\begin{vmatrix}a&b\\c&d\end{vmatrix} ​kakc​bd​ ​=k ​ac​bd​ ​
4. 若行列式的某一行(列)的为两组数之和，则可表示为两行列式之和。
   ∣ a 1 + a 2 b c 1 + c 2 d ∣ = ∣ a 1 b c 1 d ∣ + ∣ a 2 b c 2 d ∣ \begin{vmatrix}a_1+a_2&b\\c_1+c_2&d\end{vmatrix}=\begin{vmatrix}a_1&b\\c_1&d\end{vmatrix}+\begin{vmatrix}a_2&b\\c_2&d\end{vmatrix} ​a1​+a2​c1​+c2​​bd​ ​= ​a1​c1​​bd​ ​+ ​a2​c2​​bd​ ​
5. 把行列式的某一行(列)所有元素同乘以数 $k$ 都加到另一行(列)对应的元素上去，行列式的值不变。
   ∣ a b c d ∣ = ∣ a + k b b c + k d d ∣ \begin{vmatrix}a&b\\c&d\end{vmatrix}=\begin{vmatrix}a+kb&b\\c+kd&d\end{vmatrix} ​ac​bd​ ​= ​a+kbc+kd​bd​ ​
6. 矩阵乘积的行列式等于行列式的乘积：$\det (AB)=(\det A)(\det B)=\det (BA)$

推论：

1. 行列式中若有两行(列)元素相同，该行列式的值为零。
2. 行列式中某一行(列)的公因子可以提取到行列式符号外面。
3. 行列式中若有两行(列)元素成比例，则此行列式等于零。
4. $\det (kA)=k^n\det A$

由上面的性质，我们很容易得到：

1. 出现零行和零列的行列式为零。
2. 对角阵 $A=\text{diag}({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)$ 的行列式 $\det A={\lambda }_1{\lambda }_2\cdots {\lambda }_n$ 。
3. 如果 $A$ 是三角阵，行列式为主对角线元素的乘积。

对于高阶行列式，一般利用行列式的性质，初等变换化为三角行列式求解。

示例：可用数学归纳法证明范德蒙行列式(Vandermonde determinant)：
∣ 1 1 ⋯ 1 a 1 a 2 ⋯ a n a 1 2 a 2 2 ⋯ a n 2 ⋮ ⋮ ⋮ ⋮ a 1 n − 1 a 2 n − 1 ⋯ a n n − 1 ∣ = ∏ 1 ⩽ i < j ⩽ n ( a j − a i ) \begin{vmatrix} 1 & 1& \cdots &1 \\ a_1 &a_2&\cdots &a_n \\ a_1^2 &a_2^2&\cdots &a_n^2 \\ \vdots &\vdots&\vdots &\vdots \\ a_1^{n-1} &a_2^{n-1}&\cdots &a_n^{n-1} \end{vmatrix}=\prod_{1⩽ i ​1a1​a12​⋮a1n−1​​1a2​a22​⋮a2n−1​​⋯⋯⋯⋮⋯​1an​an2​⋮ann−1​​ ​=1⩽i<j⩽n∏​(aj​−ai​)

行列式函数：若 $A$ 为$n$阶矩 阵，可以将 $\det A$ 看作 $A$ 中 $n$ 个列向量的函数。若 $A$ 中除了一列之外都是固定的向量，则 $\det A$ 是线性函数。

假设第 $j$ 列是变量，定义映射 $\mathbf{x}\mapsto T(\mathbf{x})$ 为
$$T(\mathbf{x})=\det A=\det \left[\begin{array}{c}{\mathbf{a}}_1\cdots \mathbf{x}\cdots {\mathbf{a}}_n\end{array}\right]$$
则有
$$\begin{gathered} T(c\mathbf{x})=cT(\mathbf{x}) \\ T(\mathbf{u}+\mathbf{v})=T(\mathbf{u})+T(\mathbf{v}) \end{gathered}$$

克拉默法则

这里只讨论方程个数和未知数相等的$n$元线性方程组
$$A\mathbf{x}=\mathbf{b}$$
若 $\det A\ne 0$，那么它有唯一解
$$x_j=\frac{\det A_j(\mathbf{b})}{\det A},(j=1,2,\cdots ,n)$$

约定 $A_j(\mathbf{b})$ 表示用向量 $\mathbf{b}$ 替换矩阵$A$的第$j$列。

证：用${\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n$ 表示矩阵$A$ 的各列，${\mathbf{e}}_1,{\mathbf{e}}_2,\cdots ,{\mathbf{e}}_n$ 表示单位阵$I_n$ 的各列。由分块矩阵乘法
$$\begin{array}{rl}A{I}_j(\mathbf{x})& =A\left[\begin{array}{ccccc}{\mathbf{e}}_1& \cdots & \mathbf{x}& \cdots & {\mathbf{e}}_n\end{array}\right]\\ & =\left[\begin{array}{ccccc}A{\mathbf{e}}_1& \cdots & A\mathbf{x}& \cdots & A{\mathbf{e}}_n\end{array}\right]\\ & =\left[\begin{array}{ccccc}{\mathbf{a}}_1& \cdots & \mathbf{b}& \cdots & {\mathbf{a}}_n\end{array}\right]\\ & =A_j(\mathbf{b})\end{array}$$
由行列式的乘法性质
$$\det A\det I_j(\mathbf{x})=\det A_j(\mathbf{b})$$
左边第二个行列式可沿第 $j$ 列余子式展开求得 $\det I_j(\mathbf{x})=x_j$。从而
$$x_j\det A=\det A_j(\mathbf{b})$$
若 $\det A\ne 0$，则上式得证。

行列式的几何理解

Grant：行列式告诉你一个线性变换对区域的缩放比例。

我们已经知道，线性变换保持网格线平行且等距。为了方便，我们只考虑在平面直角坐标系内，单位基向量 $\mathbf{i},\mathbf{j}$ 所围成的单位正方形区域的线性变换。

根据向量加法的平行四边形法则和线性变换基本性质知，变换后的区域为矩阵 $A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$ 的列向量 $\left[\begin{array}{c}a\\ c\end{array}\right]$ 和 $\left[\begin{array}{c}b\\ d\end{array}\right]$ 为邻边的平行四边形区域。

结论：二阶行列式的值表示由 $A$ 的列确定的有向平行四边形的面积。

(1) 若 $A$ 为对角阵，显然行列式 $\det \left[\begin{array}{cc}a& b\\ 0& d\end{array}\right]$ 表示底为 $a$，高为 $d$ 的平行四边形面积

(2) 更一般的情况 $A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$ ，可以看出，行列式的值与面积有着紧密的联系。

(3) 矩阵 $\left[\begin{array}{cc}{a}^2& a\\ a& 1\end{array}\right]$ 表示将单位正方形压缩成线段，面积自然为0，行列式的值为0

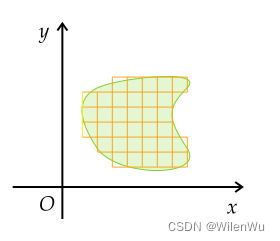
单位正方形区域缩放的比例，其实可以代表任意给定区域缩放的比例。这是因为，线性变换保持网格线平行且等距。对于空间中任意区域的面积，借助微积分的思想，我们可以采用足够的小方格来逼近区域的面积，对所有小方格等比例缩放，则整个区域也以同样的比例缩放。
$$\text{volume }T(\Omega )=(\det T)(\text{volume }\Omega )$$

通过行列式的几何意义，我们就建立了线性变换、矩阵、行列式之间的关系。不难得出

1. 复合线性变换缩放的比例相当于每次变换缩放比例的乘积，即
   $$\det AB=\det A\det B$$
2. 行列式的值为零，表示将空间压缩到更低的维度，矩阵的列向量线性相关