排序算法 - 堆排序详解

预备知识

堆是具有以下性质的完全二叉树：

• 每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆。
• 每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。
• 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。

如图：

同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子

特点

该数组从逻辑上讲就是一个堆结构，要查找数组中某个数的父结点和左右孩子结点，设数组索引为i，那么

• 父结点索引：(i-1)/2
• 左孩子索引：2*i+1
• 右孩子索引：2*i+2

可得

大顶堆特点：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] // i 对应第几个节点，i从0开始编号
小顶堆特点：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] // i 对应第几个节点，i从0开始编号

堆排序基本思想及步骤

堆排序的基本思想

1. 将待排序序列构造成一个大顶堆。
2. 此时，整个序列的最大值就是堆顶的根节点。
3. 将其与末尾元素进行交换，此时末尾就为最大值。
4. 然后将剩余n-1个元素重新构造成一个大顶堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

堆排序步骤图解说明

步骤一 ：构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

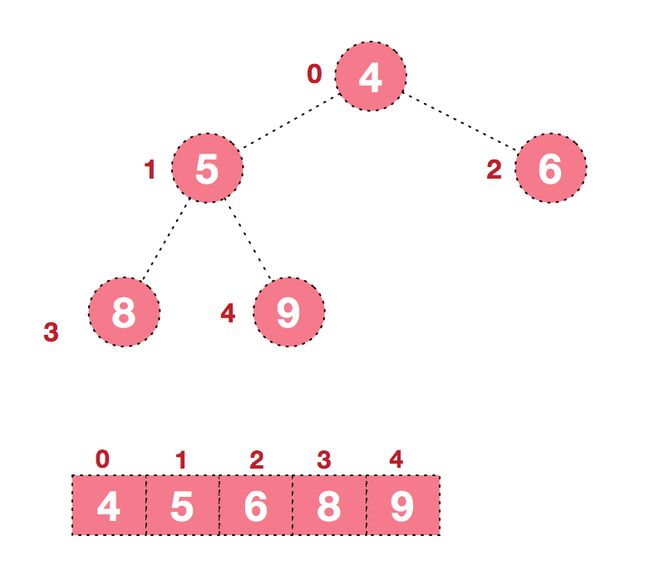
1、原始序列 [4,6,8,5,9] 对应的完全二叉树结构如下：

2、在这个完全二叉树中，结点5、9、8是叶子结点，它们没有左右孩子，所以它们满足堆的定义。我们从最后一个非叶子结点开始（最后一个非叶子结点索引为 arr.length/2-1 = 5/2-1 = 1，也就是下面的6结点），从右至左，从下至上进行调整。也就是从结点6开始，按6、4的顺序开始调整。

最后一个叶子节点的索引值是n-1，它的父节点索引值是[(n-1)-1]/2 = n/2 -1

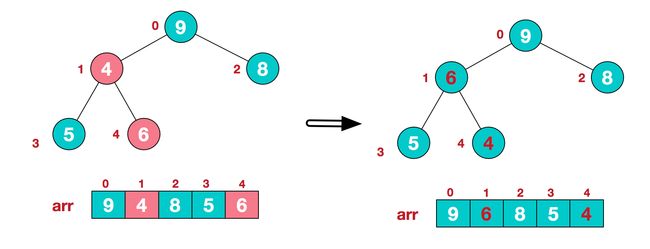
调整最后一个非叶子结点6，和左右孩子较大值的交换，由于[6,5,9]中9元素最大，所以 6 和 9 交换，如下图：

3、继续比较下一个非叶子节点4，由于[4,9,8]中9元素最大，4和9交换。

这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。直到此非叶子结点下每个结点的值都大于或等于其左右孩子结点的值

此时，我们就将一个无需序列构造成了一个大顶堆。

步骤二： 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

1、将堆顶元素9和末尾元素4进行交换

2、将数组剩余元素（实线部分）重新调整结构，使其继续满足堆定义

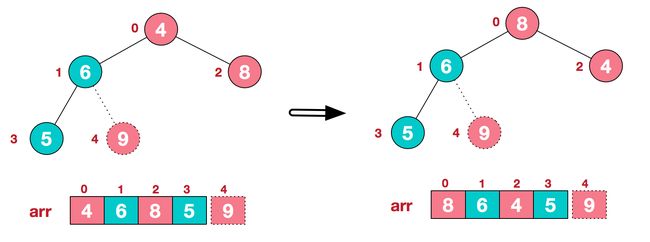
3、再将堆顶元素8与末尾元素5进行交换，得到第二大元素8

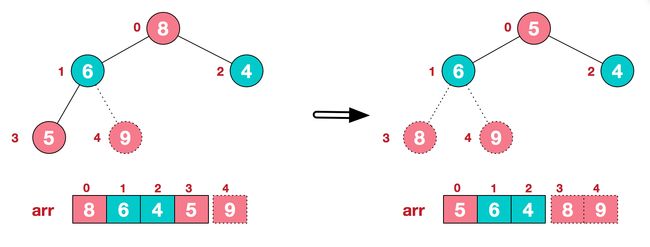
后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

堆排序执行过程描述(以大顶堆为例)如下

1. 从无序序列所确定的完全二又树的最后一个非叶子结点开始，从右至左，从下至上，对每个结点进行调整，最终将得到一个大顶堆。（根据升序降序需求选择大顶堆或小顶堆）
2. 对结点的调整方法：将当前结点(假设为a)的值与其孩子结点进行比较，如果存在大于a值的孩 子结点，则从中选出最大的一个与a交换。当a来到下一层的时候重复上述过程，直到a的孩子结点值都小于a的值为止。
3. 将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
4. 将剩余元素继续重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

代码实现

/**
 * @ClassName HeapSort
 * @author: shouanzh
 * @Description 堆排序
 * @date 2022/5/17 19:24
 */
public class HeapSort {

    public static void main(String[] args) {

        int[] array = new int[]{4, 6, 8, 5, 9};

        heapSort(array);

        System.out.println(Arrays.toString(array)); // [4, 5, 6, 8, 9]

    }


    /**
     * 堆排序 升序
     * @param array
     */
    public static void heapSort(int[] array) {

        int temp;

        // 这个for循环才是把整个数组调整成大顶堆
        // 最后一个非叶子节点开始  为 n/2 -1 即 array.length / 2 - 1
        // 调整顺序从右至左、从下至上
        for (int i = array.length / 2 - 1; i >= 0; i--) {
            adjustHeap(array,i,array.length);
        }

        // 数组已经调整为大顶堆了，将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
        for (int j = array.length - 1; j > 0; j--) {
            // 交换堆顶元素和数组末尾元素
            temp = array[j];
            array[j] = array[0];
            array[0] = temp;

            // 数组剩余的元素调成大顶堆，直接从堆顶开始调整
            // 因为该树下面的每一颗子树都已经是大顶堆了
            // 把array[0]调整到该树合适的位置，让该树继续是一个大顶堆
            adjustHeap(array,0, j);
        }


    }


    /**
     *
     * 是将i对应的非叶子节点为根的树调整成大顶堆
     * 从上往下，逐层比较，最后找到array[i]合适的位置
     *
     * @param array 待调整的数组
     * @param i 表示非叶子结点在数组中的索引
     * @param length 表示对多少个元素调整，length在逐渐减少
     */
    public static void adjustHeap(int[] array, int i, int length) {

        // i对应的非叶子节点的值
        int temp = array[i];

        // 开始调整
        // k = i * 2 + 1 指向的i结点的左子结点
        for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {

            if (k + 1 < length && array[k] < array[k + 1]) { // 说明左子结点 < 右子结点的值
                k++; // k指向右子结点
            }

            if (array[k] > temp) { // 如果子结点大于父节点
                array[i] = array[k]; // 把较大的值赋给非叶子结点
                i = k; // i指向k 然后继续循环比较
            } else {
                // 左右子结点小于父节点， 满足堆结构定义。
                // 这里break是因为就是从最后一个非叶子节点开始向上，所以到了上面的父节点也不用再比较下面的子节点
                break;
            }

        }

        // 当for循环结束后，已经将以i为父节点的树的最大值放到了最顶
        // 将temp放到调整后的位置
        array[i] = temp;

    }

}