算法与设计分析--实验一
蛮力算法的设计与分析(暴力)
这次是某不知名学院开学课程的第一次实验,一共5道题,来自力扣
第一题.216组合总和*力扣题目链接
第一道题是经典的树型回溯
class Solution {
public:
vector> combinationSum3(int k, int n) {
}
}; 首先我们要知道,力扣上都是核心代码模式,也就是说你只要实现其中的核心部分,一般是一个函数或者结构,不用你从新开始写头文件之类的,比如这里需要你实现的函数就是这个combinationSum3 (计数总和3)。
需要的返回值是一个二维动态数组(c++代码)
右上角可以选择代码模式,这里以C++为例
先看一遍题目描述:
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。
解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
也就是说,我们输出的组合不能重复,顺序无关
这道题就是dfs组合计数的升级版
因为时间效率低,所以题目数据不会很大,数据大了就得换其他方法了
先看一遍递归实现排列型枚举的代码
#include
using namespace std;
const int N= 10;
int path[N], n;
bool st[N];
void dfs(int u)
{
if(u>n){
for(int i = 1; i <=n; i++) cout<>n;
dfs(1);
return 0;
} 我们同理,先存储路径和答案
vector> result; // 存放结果集
vector path; // 符合条件的结果 确定终止条件
if (path.size() == k) {
if (sum == targetSum) result.push_back(path);
return;
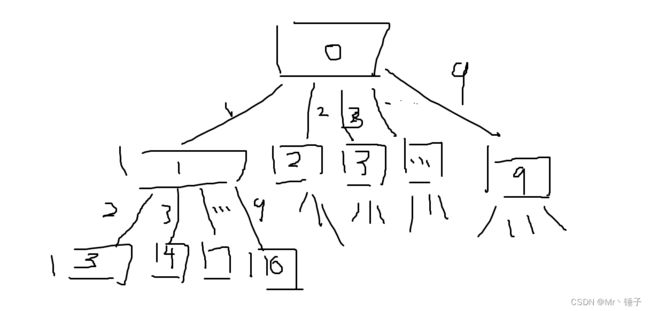
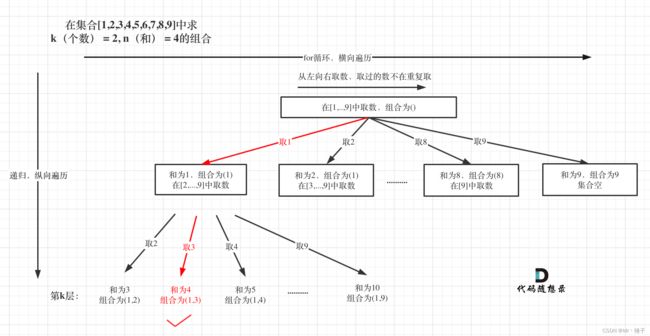
}在初学dfs(回溯)时,画一个回溯图会更好理解一点
电脑上画图还是太难了,找一个别人的图
我们可以发现,我们题目要求的K,就是树的深度
每一层都是1~9的选择, 但是我们要注意,因为答案不重复,比如3,6和6,3是属于一个答案
所以我们每一次选择数字都要从该数字的后面开始选择,比如选择了2,下一层选择的数字就是3~9
当然,我们还发现可以剪枝优化,
比如当SUM>我们的target的时候,我们就不用向下遍历了
还有就是当剩下可以选择的数字小于K了,我们也不用向下遍历了
代码+注释如下
class Solution {
private:
vector> result; // 存放结果集
vector path; // 符合条件的结果
void backtracking(int targetSum, int k, int sum, int startIndex) { //最后一个参数为开始选择的数字,防止出现重复组合
if (sum > targetSum) { // 剪枝操作1
return; // 如果path.size() == k 但sum != targetSum 直接返回
}
if (path.size() == k) { // 终止条件,可以返回了
if (sum == targetSum) result.push_back(path);
return;
}
for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝操作2
sum += i; // 处理
path.push_back(i); // 处理
backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
sum -= i; // 回溯 还原现场
path.pop_back(); // 回溯 还原现场
}
}
public:
vector> combinationSum3(int k, int n) {
backtracking(n, k, 0, 1);
return result;
}
}; 第二题.206反转链表力扣题目链接
这道题是基础中的基础了
题目描述:
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
思路也很简单 就是遍历链表 遍历链表每一个节点的时候把该节点指向前一个节点
当然,为了原链表不被打乱,我们需要一个临时节点
代码+注释如下
class Solution {
ListNode* reverse(ListNode* pre,ListNode* cur){//参数为 前节点 当前节点
if(cur == NULL)return pre; //如果是空链表 直接返回
auto temp = cur->next; //临时节点指向当前节点的下一节点 为了遍历
cur->next = pre;//当前节点指向前一节点
return reverse(cur,temp); //递归往后遍历
}
public:
ListNode* reverseList(ListNode* head) {
return reverse(NULL,head);//传入头节点
}
};第三题:1160.拼写单词力扣题目链接
先看一遍题目描述
给你一份『词汇表』(字符串数组) words 和一张『字母表』(字符串) chars。
假如你可以用 chars 中的『字母』(字符)拼写出 words 中的某个『单词』(字符串),那么我们就认为你掌握了这个单词。
注意:每次拼写(指拼写词汇表中的一个单词)时,chars 中的每个字母都只能用一次。
返回词汇表 words 中你掌握的所有单词的 长度之和。
示例 1:
输入:words = ["cat","bt","hat","tree"], chars = "atach"
输出:6
解释:
可以形成字符串 "cat" 和 "hat",所以答案是 3 + 3 = 6。
示例 2:
输入:words = ["hello","world","leetcode"], chars = "welldonehoneyr"
输出:10
解释:
可以形成字符串 "hello" 和 "world",所以答案是 5 + 5 = 10。
提示:
1 <= words.length <= 1000
1 <= words[i].length, chars.length <= 100
所有字符串中都仅包含小写英文字母
class Solution {
public:
int countCharacters(vector& words, string chars) {
}
}; 题目传入的是一个字符串动态数组,一个目标字符串
这道题出在这样有点怪怪的,一开始用dfs没做出来
用类似哈希的做法就轻松搞定了
原理就是把chars里的每一个字母进行计数,当目标单词中每个字母计数不为0时,则证明能拼出这个单词
代码+注释如下:
class Solution {
public:
int countCharacters(vector& words, string chars) {
int m[26]; // 计数,类哈希表,保存chars每个字母出现的次数
memset(m, 0, sizeof(m)); //不是全局变量 得初始化
for (char ch : chars) {
m[ch-'a'] ++; //计数
}
int ret = 0;
for (auto word : words) {
int temp[26];
memcpy(temp, m, sizeof(m));
bool canSpell = true;
for (char ch : word) {
if (temp[ch-'a'] == 0) {
canSpell = false;
break;
}
temp[ch-'a'] --;
}
if (canSpell) {
ret += word.size();
}
}
return ret;
}
}; 第四题
1475. 商品折扣后的最终价格
题目描述:
给你一个数组 prices ,其中 prices[i] 是商店里第 i 件商品的价格。
商店里正在进行促销活动,如果你要买第 i 件商品,那么你可以得到与 prices[j] 相等的折扣,其中 j 是满足 j > i 且 prices[j] <= prices[i] 的 最小下标 ,如果没有满足条件的 j ,你将没有任何折扣。
请你返回一个数组,数组中第 i 个元素是折扣后你购买商品 i 最终需要支付的价格。
示例 1:
输入:prices = [8,4,6,2,3]
输出:[4,2,4,2,3]
解释:
商品 0 的价格为 price[0]=8 ,你将得到 prices[1]=4 的折扣,所以最终价格为 8 - 4 = 4 。
商品 1 的价格为 price[1]=4 ,你将得到 prices[3]=2 的折扣,所以最终价格为 4 - 2 = 2 。
商品 2 的价格为 price[2]=6 ,你将得到 prices[3]=2 的折扣,所以最终价格为 6 - 2 = 4 。
商品 3 和 4 都没有折扣。
示例 2:
输入:prices = [1,2,3,4,5]
输出:[1,2,3,4,5]
解释:在这个例子中,所有商品都没有折扣。
示例 3:
输入:prices = [10,1,1,6]
输出:[9,0,1,6]
提示:
1 <= prices.length <= 500
1 <= prices[i] <= 10^3
简单题,我们可以完全按照题目意思写一个二重循环遍历就好
数据也不大,暴力就能过(废话,不能怎么叫暴力算法试验报告)
class Solution {
public:
vector finalPrices(vector& prices) {
vector res; //不改变原数组 开个数组存答案
bool flag = true; //判断是否加入答案
for(int i = 0; i < prices.size(); i ++ )
{
for(int j = 1; j < prices.size(); j ++ )
{
if(j > i && prices[j] <= prices[i]) // 题目给的条件照抄
{
res.push_back(prices[i] - prices[j]);
flag = false;
break;
}
}
if(flag)
res.push_back(prices[i]);
else
flag = true;
}
return res;
}
}; 看了一下评论,这道题单调栈也能做,时间复杂度能优化到O(n)
class Solution {
public:
vector finalPrices(vector& prices) {
//维护一个价格单调递增的栈存储索引值
//若当前价格小于栈顶所指价格,则栈顶索引值出栈,计算该索引处折扣后的价格,直到栈为空或当前价格大于栈顶所指价格
//将当前索引入栈
if(prices.empty()) return {};
stack s;
int len=prices.size();
vector ans(len);
s.push(0); //将第一个元素的索引入栈
for(int i=1;i 第五题
1518. 换水问题
题目描述:
小区便利店正在促销,用 numExchange 个空酒瓶可以兑换一瓶新酒。你购入了 numBottles 瓶酒。
如果喝掉了酒瓶中的酒,那么酒瓶就会变成空的。
请你计算 最多 能喝到多少瓶酒。
输入:numBottles = 9, numExchange = 3
输出:13
解释:你可以用 3 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 9 + 3 + 1 = 13 瓶酒。
输入:numBottles = 15, numExchange = 4
输出:19
解释:你可以用 4 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 15 + 3 + 1 = 19 瓶酒。
示例 3:
输入:numBottles = 5, numExchange = 5
输出:6
示例 4:
输入:numBottles = 2, numExchange = 3
输出:2
提示:
1 <= numBottles <= 100
2 <= numExchange <= 100
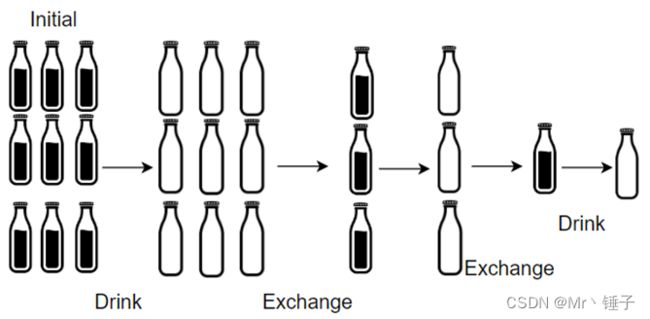
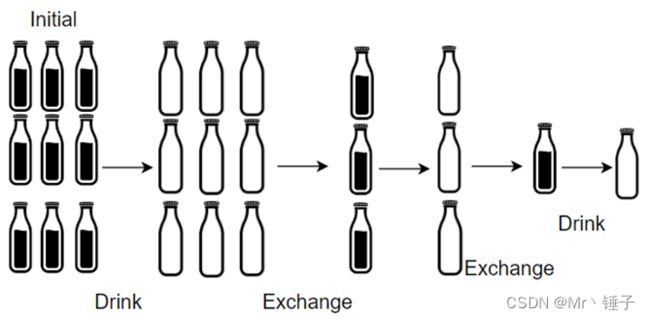
看着题目很复杂,实际上那是非常非常的简单,之前的题目瓶盖还能换酒,这个只有瓶子能换酒
大一的C语言基础题都比这难
不说了,直接上代码和注释,看完应该都能懂 也不用什么优化了,暴力算法已经超越100%了,这题基数小,暴力最快
class Solution {
public:
int numWaterBottles(int numBottles, int numExchange) {
int res = 0; //存答案
int temp = numBottles; // 存初始瓶数
res += numBottles;
while(temp >= numExchange) //如果剩下的瓶子换不了就结束
{
res += temp / numExchange;
int temp2 = temp % numExchange; // 记得要加上上一轮换不了的余数
temp /= numExchange;
temp += temp2;
}
return res;
}
};总结:
新学期算法课的第一次试验,除了第一题有难度,其他基本是拿来凑数的
第一题是搜索和回溯,也是真正“暴力”算法的样子,其他的更多像一个模拟题,复述题目内容就好
半年了,学校蓝桥杯的报名费都还没报销,真是对自己学算法的同学极大的鼓励啊