radix-tree算法浅析--从不懂到装懂

前言 本文为原创，可能会存在一些知识点或理解上的问题，欢迎切磋和交流  ^_^

1. 为什么要研究radix-tree算法？(脑残吗)

存储的核心就是I/O流，不懂I/O流就不要说自己会存储；而最近一直研究和分析文件系统I/O流，说到I/O瓶颈和提升性能，缓存读写显然是重中之重。在分析ceph文件系统写I/O流程中，比如调用ceph_write_iter接口，如果过缓存，必调用generic_perform_write()，这个接口的作用是啥呢，就是通过索引在页缓存中返回一个页(不管你是在页缓存中找到的一个页，还是因没有找到，自己重新申请并加到页缓存结构中的，这个后面详细说)，把用户态缓存区的数据拷贝到这个页中，然后返回给用户态说，哥们，我写完了(当然，此时的数据只是在内存中，需要内核线程定时下刷数据落盘，才是真正的写数据到磁盘介质)。

那么，我的问题是，这一个页又是存放在什么数据结构里呢，实现的算法又是怎样的呢？

带着这些疑问，继续查看调用到的接口，最后发现所有有关页操作(创建、删除、查找)有一个专门的文件lib/radix-tree.c用于管理和维护，这套算法已经屏蔽了上层具体业务(页缓存机制、还是网络路由机制等等)，是完完全全的底层核心算法，这勾起了我极大的好奇心，这一份诱惑难以拒绝，抱着对金庸“九阴真经”的痴迷，亦或是对“淡眉如秋水，玉肌伴轻风”的眷恋，所以想一窥她的芳容。

Radix-tree树算法是对字典树算法的压缩变种，前面分析字典树算法的目的就在这里，不过字典树算法原理很好理解，接口代码不过200行，但实现radix-tree算法的内容就太多了。感觉自己的脑折叠度不够。。。

Radix-tree基数树用于存储与查找键-值(key-value)这种关联类型的数据结构。当然，键(key)可以是字符串，也可以是长整型数据类型的路由(比如id)，利用raidx-tree可以快速完成其对应的value值。所以linux内核网络路由查找就是用基数树算法实现，内存管理页缓存机制也用到了该数据结构。

Linux内核使用基数树管理与地址空间相关的所有页，页缓存读写获取的页都存放到这个树结构中，主要目的是加大搜索和管理缓存页效率，提高IO缓存读写性能。Radix-tree并不对应一个普通的二叉或三叉树，而是一个多叉树，同时它又是不平衡的，即树的每个节点，高度差可能是任意值，树本身由两种数据结构组成，即radix_tree_root和radix_tree_node，因为页缓存叶子节点存放的是一个页，所以struct page页是基数树的一个实例。

2.radix-tree相关结构体

从面向对象语言的设计原则看，结构体就是一个类，尤其内核中用到的结构体，里面即有公共成员变量，又有自己私有成员变量，同时封装了函数操作集，用于操作本类对象的方法。所以搞明白结构体中成员的作用，对于理解函数接口是干嘛的，起到画龙点睛的作用。但是，有些结构体，比如说struct inode、struct mount等等，动辄十几、几十个成员，如果不是负责开发和维护内核模块，我们在平时使用中，知道其中几个主要的，就可以了。以下针对radix-tree算法主要涉及的两个结构体进行分析。

注意：以下结构体和相关源码均基于内核源码版本kernel-4.14.28-201.el7。

2.1 struct radix_tree_root(include/linux/radix-tree.h)

struct radix_tree_root {
	gfp_t			gfp_mask;
	struct radix_tree_node	__rcu *rnode;
};

如何理解struct radix_tree_root结构体以及成员？

针对这部分结构体的认识，鉴于相关资料(《深入linux内核架构》、《基于2.6.x的存储技术原理分析》以及网上资料等)。

radix_tree_root是每个基数树的根节点，radix-tree树开始于这个根节点的建立，我认为可以把它解释为一个头节点更容易理解。gfp_mask查看相关资料，给出的结论是一个标记，用于区分内存区域，具体如何用，我没有具体看，可留一个遗留问题，待续。rnode结构体指针指向基数树的第一个节点。

2.2 struct radix_tree_node(include/linux/radix-tree.h)

#define RADIX_TREE_MAX_TAGS 3

#ifndef RADIX_TREE_MAP_SHIFT
#define RADIX_TREE_MAP_SHIFT	(CONFIG_BASE_SMALL ? 4 : 6)
#endif

#define RADIX_TREE_MAP_SIZE	(1UL << RADIX_TREE_MAP_SHIFT)
#define RADIX_TREE_MAP_MASK	(RADIX_TREE_MAP_SIZE-1)

struct radix_tree_node {
	unsigned char	shift;		/* Bits remaining in each slot */
	unsigned char	offset;		/* Slot offset in parent */
	unsigned char	count;		/* Total entry count */
	unsigned char	exceptional;	/* Exceptional entry count */
	struct radix_tree_node *parent;		/* Used when ascending tree */
	struct radix_tree_root *root;		/* The tree we belong to */
	union {
		struct list_head private_list;	/* For tree user */
		struct rcu_head	rcu_head;	/* Used when freeing node */
	};
	void __rcu	*slots[RADIX_TREE_MAP_SIZE];
	unsigned long	tags[RADIX_TREE_MAX_TAGS][RADIX_TREE_TAG_LONGS];
};

基数树使用struct radix_tree_node结构体定义了中间节点，先介绍一下slots指针数组，数组个数是由宏RADIX_TREE_MAP_SIZE来定义，RADIX_TREE_MAP_SIZE宏定义为(1UL << RADIX_TREE_MAP_SHIFT)， RADIX_TREE_MAP_SHIFT按照内核配置参数CONFIG_BASE_SMALL是否设置，被定义为4或者6，即如果CONFIG_BASE_SMALL被设置，RADIX_TREE_MAP_SIZE为16，否则为64。数组的每一个元素存储的是下一个radix_tree_node节点或叶子，而叶子在页缓存存储的就是一个页page的地址；count计数表示的是这个节点中slot数组元素被使用的数目；基数树中每一个节点slot数组又可以指向16或64个节点或叶子，每个叶子表示一个页，但是此时内核不能区分出这个页是脏页还是干净页，为进一步提高对脏页和干净页操作，引入了tags二维数组。shift表示当前查询或插入节点所在整颗树的层数；offset表示存储当前节点在父节点中的偏移。

遗留问题：

tag二维数组不是很理解其发挥的作用，RADIX_TREE_MAX_TAGS 源码中定义为3，即内核支持三种形式的tag，RADIX_TREE_TAG_LONGS被定义如下

#define RADIX_TREE_TAG_LONGS  ((RADIX_TREE_MAP_SIZE + BITS_PER_LONG - 1) / BITS_PER_LONG)，BITS_PER_LONG被定义为32或64，假设BITS_PER_LONG为64，RADIX_TREE_MAP_SIZE值为64，RADIX_TREE_TAG_LONGS值为(64+64-1)/64=1，那么tag二维数组为tag[3][1]，即为一维数组，总共3个元素，如何存的下整个slots 64个叶子的标记？

3.radix-tree插入函数分析

radix-tree算法源码文件在kernel/lib/radix-tree.c文件中，这里的源码分析目前只是看代码流程，函数实现等方式进行理论分析，其中结构体有些成员赋值仍不知所以然其意义。采用热探测方式进行打桩调试，因为该算法摒弃上层具体业务，所以内核会无时无刻将查到的条目信息打印出来，无法通过添加调试信息方式进行动态分析，其他调试方式暂时没有想到，如果有好的方式，可以讨论沟通一下。以下主要从代码层面讲解插入一个条目信息的流程，其中有些公共接口会放到前面简单讲解一下。

注意：以下结构体和相关源码均基于内核源码版本kernel-4.14.28-201.el7。

3.1 static unsigned radix_tree_load_root(const struct radix_tree_root *root, struct radix_tree_node **nodep, unsigned long *maxindex)

static unsigned radix_tree_load_root(const struct radix_tree_root *root,
		struct radix_tree_node **nodep, unsigned long *maxindex)
{
	struct radix_tree_node *node = rcu_dereference_raw(root->rnode);

	*nodep = node;

	if (likely(radix_tree_is_internal_node(node))) {
		node = entry_to_node(node);
		*maxindex = node_maxindex(node);
		return node->shift + RADIX_TREE_MAP_SHIFT;
	}

	*maxindex = 0;
	return 0;
}

分析一个函数先从函数返回值、函数入参出参说起，函数参数一共有3个，struct radix_tree_root *root、radix_tree_node *child、unsigned long maxindex，很明显root是入参，所有radix-tree函数入参一定要获取根节点root，child和maxindex是出参，所以该函数用于获取根节点，先通过rcu_dereference_raw获取root指向的rnode成员并返回给一个局部变量node，通过radix_tree_is_internal_node(node))判断节点node是否是内部节点，如果是内部节点，再通过entry_to_node获取rnode对应radix-tree的指针并再赋值给node，通过node_maxindex获取对应当前节点的最大索引范围，比如当前是第一个radix_tree_node节点，即第一层，所以maxindex=64，因为该节点slot数组共64个元素，可以指向64个叶子，此处赋值给maxindex，函数返回值为当前节点对应的shift值，此处shift大小为0+64=64。如果判断发现该节点不是内部节点，则maxindex=0，返回shift=0。

3.2 static inline struct radix_tree_node *entry_to_node(void *ptr)

static inline struct radix_tree_node *entry_to_node(void *ptr)
{
	return (void *)((unsigned long)ptr & ~RADIX_TREE_INTERNAL_NODE);
}

该函数用于获取函数参数对应的radix-tree的节点，我的理解是通过传入参是否含有标志RADIX_TREE_INTERNAL_NODE是否是一个内部节点还是叶子节点，此处是ptr & ~RADIX_TREE_INTERNAL_NODE，很明显是要把该标志清除，所以该函数只是想将传入参的身份，即内部节点重新清除一下。目的是便于后面流程以该节点为起始节点进行操作。

3.3 static inline void *node_to_entry(void *ptr)

static inline void *node_to_entry(void *ptr)
{
	return (void *)((unsigned long)ptr | RADIX_TREE_INTERNAL_NODE);
}

node_to_entry函数和entry_to_node函数作用刚好相反，从函数名称上也可以看出来，该函数作用是将传入值指向节点的指针的低位或上RADIX_TREE_INTERNAL_NODE,用于告诉大家这个节点已经是一个内部节点了，即标识了该节点的身份。

3.4 int __radix_tree_insert(struct radix_tree_root *root, unsigned long index, unsigned order, void *item)

int __radix_tree_insert(struct radix_tree_root *root, unsigned long index,
			unsigned order, void *item)
{
	struct radix_tree_node *node;
	void __rcu **slot;
	int error;

	BUG_ON(radix_tree_is_internal_node(item));

	error = __radix_tree_create(root, index, order, &node, &slot);
	if (error)
		return error;

	error = insert_entries(node, slot, item, order, false);
	if (error < 0)
		return error;

	if (node) {
		unsigned offset = get_slot_offset(node, slot);
		BUG_ON(tag_get(node, 0, offset));
		BUG_ON(tag_get(node, 1, offset));
		BUG_ON(tag_get(node, 2, offset));
	} else {
		BUG_ON(root_tags_get(root));
	}

	return 0;
}

对该函数的理解，先从参数说起，其中root是基数树根节点，index是一个索引值，是上层业务传下来的，比如页缓存写流程中，当执行echo 123 > file命令时，此时先到页缓存中查找页是否命令，这个index值的作用是用户态写入字节流的偏移被转换到页缓存中一个页在缓存中的索引；order上层函数传下来的是一个0，不用管；item是要存入的条目信息。首先，radix-tree中节点类型有两种：中间节点和叶子节点。BUG_ON(radix_tree_is_internal_node(item))用于判断要插入的条目信息是否是内部节点，通过BUG_ON和radix_tree_is_internal_node插入的条目信息不能是内部节点，如果是，则直接报错，即插入的必须是一个叶子节点。__radix_tree_create()会返回获取新索引对应的父节点指针和slot指针。 insert_entries()则是将最终要写到叶子节点上的item条目信息赋值给slot指针指向的节点。

3.5 static inline bool radix_tree_is_internal_node(void *ptr)

#define RADIX_TREE_ENTRY_MASK		3UL
#define RADIX_TREE_INTERNAL_NODE	1UL
static inline bool radix_tree_is_internal_node(void *ptr)
{
	return ((unsigned long)ptr & RADIX_TREE_ENTRY_MASK) ==
				RADIX_TREE_INTERNAL_NODE;
}

其中，有关slot最低两个bit位的意义如下所示(源于include/linux/radix-tree.h)，如下图所示：

The bottom two bits of the slot determine how the remaining bits in the
 * slot are interpreted:
 *
 * 00 - data pointer
 * 01 - internal entry
 * 10 - exceptional entry
 * 11 - this bit combination is currently unused/reserved

所以，slot最低两个bit用于决定slot保留的bit位数据类型，所以radix_tree_is_internal_node()中先获取最低bit位，&上RADIX_TREE_INTERNAL_NODE，如果为1，则说明这是一个内部节点，如果为0，则不是一个内部节点。

3.6 int __radix_tree_create(struct radix_tree_root *root, unsigned long index, unsigned order, struct radix_tree_node **nodep, void __rcu ***slotp)

int __radix_tree_create(struct radix_tree_root *root, unsigned long index,
			unsigned order, struct radix_tree_node **nodep,
			void __rcu ***slotp)
{
	struct radix_tree_node *node = NULL, *child;
	void __rcu **slot = (void __rcu **)&root->rnode;
	unsigned long maxindex;
	unsigned int shift, offset = 0;
	unsigned long max = index | ((1UL << order) - 1);
	gfp_t gfp = root_gfp_mask(root);

	shift = radix_tree_load_root(root, &child, &maxindex);

	/* Make sure the tree is high enough.  */
	if (order > 0 && max == ((1UL << order) - 1))
		max++;
	if (max > maxindex) {
		int error = radix_tree_extend(root, gfp, max, shift);
		if (error < 0)
			return error;
		shift = error;
		child = rcu_dereference_raw(root->rnode);
	}

	while (shift > order) {
		shift -= RADIX_TREE_MAP_SHIFT;
		if (child == NULL) {
			/* Have to add a child node.  */
			child = radix_tree_node_alloc(gfp, node, root, shift,
							offset, 0, 0);
			if (!child)
				return -ENOMEM;
			rcu_assign_pointer(*slot, node_to_entry(child));
			if (node)
				node->count++;
		} else if (!radix_tree_is_internal_node(child))
			break;

		/* Go a level down */
		node = entry_to_node(child);
		offset = radix_tree_descend(node, &child, index);
		slot = &node->slots[offset];
	}
	if (nodep)
		*nodep = node;
	if (slotp)
		*slotp = slot;
	return 0;
}

到了__radix_tree_create函数，个人认为，这个函数可以说是整个__radix_tree_index函数的核心，也是最不好理解的函数。因为其他的函数作用都很简单，通过看函数名称就可以知道函数做了什么，层次比较清晰，但是create函数，看完也只是知道大概做了什么，这棵树是如何生长的，还是不清楚，另外这个函数涉及内容很多，它的作用是在树中找到我想要找的节点node和该node对应的slot指针，便于把传进来的条目信息写到slot指针指向的一块内存区域。

这个函数干了这么几件事：

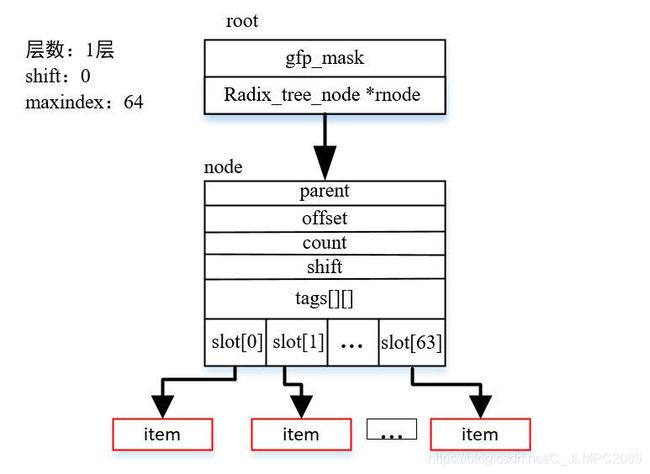
(1) 先找到root对应rnode节点赋值给child、当前节点的maxindex最大索引值，并返回当前节点对应的shift。索引值index怎么理解？Shift怎么理解？比如第一层节点，应该是如下图所示：

该层是第一层，即只有一个节点，那么slot数组一共可以存放64个叶子，所以，maxindex=64，shift值表示slot指向的每一个元素指针所在整颗树的第几层，比如这64个元素均在第0层，所以shift=0。

(2) 注意max局部变量，unsigned long max = index | ((1UL << order) - 1)，通过计算可知，max就是上层透传下来的index，可以理解成max=index，通过判断max和maxindex，当前树层深maxindex是否满足要插入元素的索引值，如果满足，则直接跳过if处理逻辑，如果不满足，则需要扩展树深度，我们假设这里满足，先不扩展。

(3) While(shift > order)循环语句体，order透传下来值=0，shift=64，child指向第一个radix_tree_node节点，进入循环语句内容，shift先减64，变为0，然后判断child是否为NULL，显然不为NULL，再判断child是否内部节点，也显然是，所以两个if语句跳过。

(4) 执行entry_to_node函数，清除内部节点标志RADIX_TREE_INTERNAL_NODE，获取该指针对应radix_tree的节点。

(5) 通过radix_tree_descend()函数找到node节点中slot数组偏移index个元素的指针，并返回这个指针相对该node的偏移offset，将该值赋值给slot指针。

(6) 然后执行第二遍循环，此时shift=0，shift>order条件不成立，退出循环体。

(7) 此时就找到了想要插入条目信息的元素，并赋值给出参nodep和slotp。

以上步骤是查找要插入内存获取对应指针的一般流程，如果是一层，即shift=0，则while循环语句每一次都只循环一次即可，插入64个元素，刚好把64个slot元素全部填满。如果要插入索引值大于maxindex，则需要扩展树高度，另外，查找节点需要循环多次，该流程后面会以流程框架图方式呈现出来。

3.7 static inline unsigned long node_maxindex(const struct radix_tree_node *node)

static inline unsigned long node_maxindex(const struct radix_tree_node *node)
{
	return shift_maxindex(node->shift);
}
其中shift_maxindex函数实现如下
static inline unsigned long shift_maxindex(unsigned int shift)
{
	return (RADIX_TREE_MAP_SIZE << shift) - 1;
}

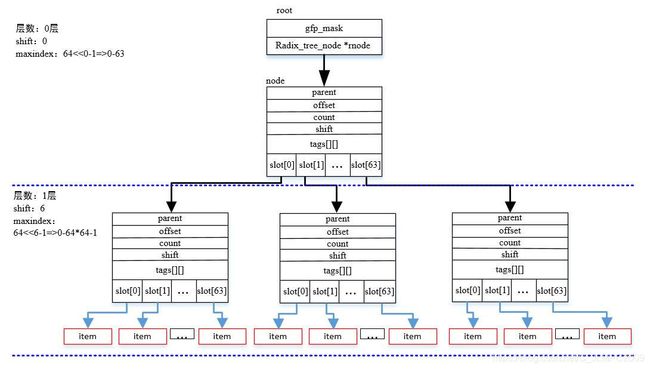
该函数作用是获取当前节点所在该层能够支持的最大索引值，前面已经举例，当只有一个节点时，该层支持最大索引值为64，如果是两层，支持最大索引值为多少，如下图所示：

第2层支持maxindex为64<<6-1个元素。

疑问：这里其实有个疑问，shift值是如何知道的？Shift值在源码中确实没有体现出来，我是根据代码逻辑推算出来的，发现刚好符合以上规律。

3.8 static inline unsigned long shift_maxindex(unsigned int shift)

static inline unsigned long shift_maxindex(unsigned int shift)
{
	return (RADIX_TREE_MAP_SIZE << shift) - 1;
}

该函数作用是返回当前节点所在层的最大索引值。

3.9 static int radix_tree_extend(struct radix_tree_root *root, gfp_t gfp, unsigned long index, unsigned int shift)

/*
 *	Extend a radix tree so it can store key @index.
 */
static int radix_tree_extend(struct radix_tree_root *root, gfp_t gfp,
				unsigned long index, unsigned int shift)
{
	void *entry;
	unsigned int maxshift;
	int tag;

	/* Figure out what the shift should be.  */
	maxshift = shift;
	while (index > shift_maxindex(maxshift))
		maxshift += RADIX_TREE_MAP_SHIFT;

	entry = rcu_dereference_raw(root->rnode);
	if (!entry && (!is_idr(root) || root_tag_get(root, IDR_FREE)))
		goto out;

	do {
		struct radix_tree_node *node = radix_tree_node_alloc(gfp, NULL,
							root, shift, 0, 1, 0);
		if (!node)
			return -ENOMEM;

		if (is_idr(root)) {
			all_tag_set(node, IDR_FREE);
			if (!root_tag_get(root, IDR_FREE)) {
				tag_clear(node, IDR_FREE, 0);
				root_tag_set(root, IDR_FREE);
			}
		} else {
			/* Propagate the aggregated tag info to the new child */
			for (tag = 0; tag < RADIX_TREE_MAX_TAGS; tag++) {
				if (root_tag_get(root, tag))
					tag_set(node, tag, 0);
			}
		}

		BUG_ON(shift > BITS_PER_LONG);
		if (radix_tree_is_internal_node(entry)) {
			entry_to_node(entry)->parent = node;
		} else if (radix_tree_exceptional_entry(entry)) {
			/* Moving an exceptional root->rnode to a node */
			node->exceptional = 1;
		}
		/*
		 * entry was already in the radix tree, so we do not need
		 * rcu_assign_pointer here
		 */
		node->slots[0] = (void __rcu *)entry;
		entry = node_to_entry(node);
		rcu_assign_pointer(root->rnode, entry);
		shift += RADIX_TREE_MAP_SHIFT;
	} while (shift <= maxshift);
out:
	return maxshift + RADIX_TREE_MAP_SHIFT;
}

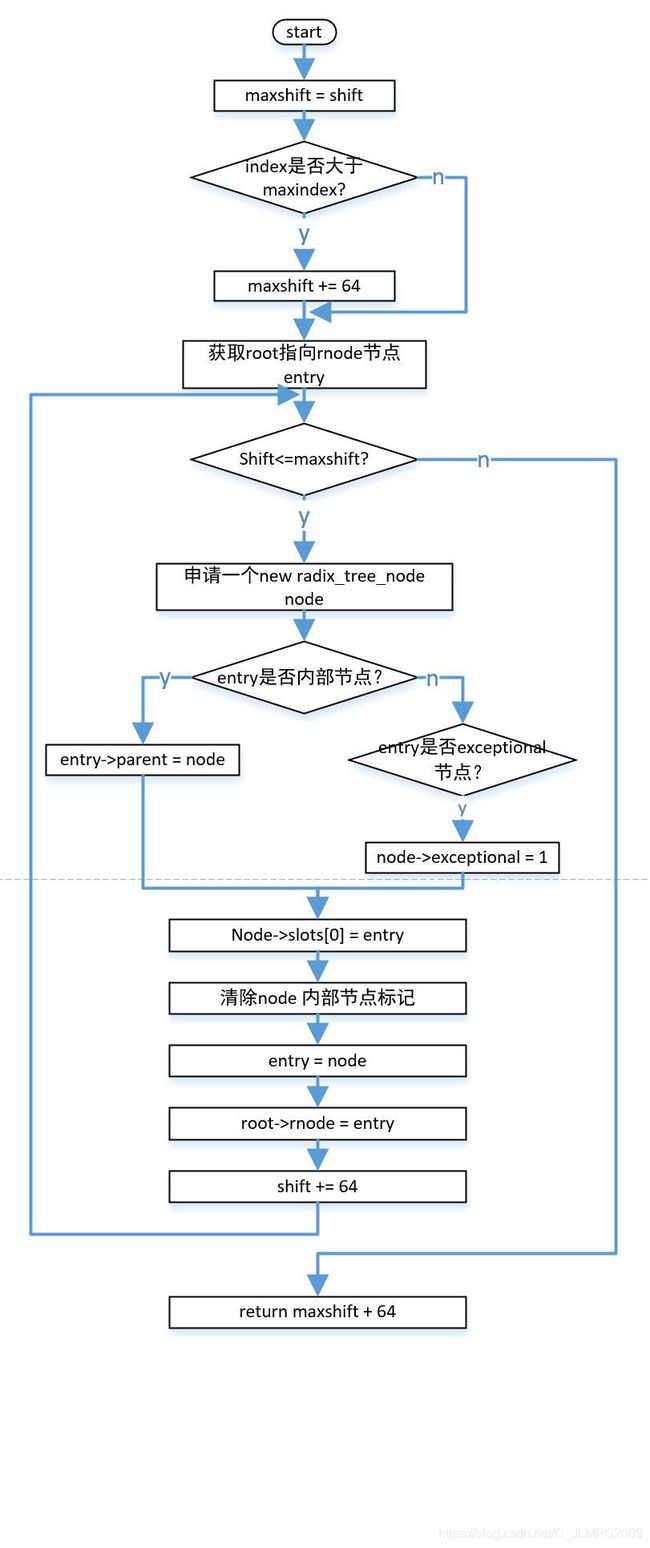
如果要插入64个元素以内，则该函数不会被调用，但是如果插入元素索引>64，则需要扩展树高度，以满足插入操作。扩展基数树之前一直没有搞懂，是因为懒得搞懂，因为要存储64个元素直接申请内存用于存储叶子节点即可，干嘛费劲研究这个，如果要存的条目索引值超过64，比如index=65，再放到树里，因为一层树深不够，一定是要扩展树的高度，那么研究一下该函数还是有必要的，这个函数和下面radix_tree_descend遥相呼应，一个用来扩展，一个用来遍历。扩展节点和索引节点的关键也是这两个函数，搞懂了就会了。直接上函数流程图如下所示：

扩展树的高度如果不仔细看，以为和普通二叉树一样，是一颗倒着长的树，往下继续添加节点就可以了。但是如下两行代码是这样写的：

当entry为内部节点是，entry_to_node(entry)->parent = node;

node->slots[0] = (void __rcu *)entry;

entry = node_to_entry(node);

rcu_assign_pointer(root->rnode, entry);

如果是一颗正常倒着生长的树，这几行代码就很怪，不符合逻辑嘛，所以简单画一下，就知道这棵树是如何生长的了，如下图所示。

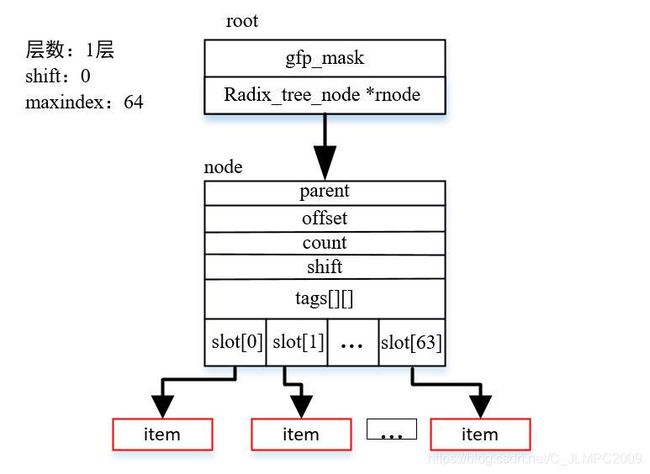
如果当前只有一层，即一个radix_tree_node节点，基数树如下所示：

此时该基数树一共可以存放64个索引对应条目信息；如果此时再插入一个index=65对应的条目信息，发现index>maxindex，就要扩展树的高度。扩展后树的样子如下图所示：

扩展后树的样子如果还是不够清晰，不妨继续修改一下，即如下图所示：

这样扩展后，基数树的样子就一目了然了。因为创建流程里还有一个while循环要找到对应index的节点，所以在要插入条目元素索引值index=65操作中，create流程while循环找对应index的节点如下图所示：

4.0 static unsigned int radix_tree_descend(const struct radix_tree_node *parent, struct radix_tree_node **nodep, unsigned long index)

static unsigned int radix_tree_descend(const struct radix_tree_node *parent,
			struct radix_tree_node **nodep, unsigned long index)
{
	unsigned int offset = (index >> parent->shift) & RADIX_TREE_MAP_MASK;
	void __rcu **entry = rcu_dereference_raw(parent->slots[offset]);

#ifdef CONFIG_RADIX_TREE_MULTIORDER
	if (radix_tree_is_internal_node(entry)) {
		if (is_sibling_entry(parent, entry)) {
			void __rcu **sibentry;
			sibentry = (void __rcu **) entry_to_node(entry);
			offset = get_slot_offset(parent, sibentry);
			entry = rcu_dereference_raw(*sibentry);
		}
	}
#endif

	*nodep = (void *)entry;
	return offset;
}

该函数逻辑比较简单，核心代码就一行：unsigned int offset = (index >> parent->shift) & RADIX_TREE_MAP_MASK，就是计算出偏移然后返回该节点slot所在偏移的指针即可。

4. radix-tree API用户态实例

demo源码如下：

 1 #include 
  2 #include 
  3 #include 
  4 
  5 #include 
  6 
  7 char *test[] = {"aaa", "bbb", "ccc"};
  8 struct radix_tree_root root;
  9 
 10 static int __init my_radix_tree_init(void)
 11 {
 12     int i = 0;
 13     int num = ARRAY_SIZE(test);
 14     RADIX_TREE(root, GFP_ATOMIC);
 15     printk("num : %d\n", num);
 16     for(i = 0; i < num; i++)
 17     {
 18         radix_tree_insert(&root, i, test[i]);
 19     }
 20     for(i = 0; i < num; i++)
 21     {
 22         printk("---[%d]---%s\n", i, (char*)radix_tree_lookup(&root, i));
 23     }
 24 
 25     return 0;
 26 }
 27 
 28 static void __exit my_radix_tree_exit(void)
 29 {
 30     printk("my_radix_tree_exit start\n");
 31 }
 32 
 33 
 34 module_init(my_radix_tree_init);
 35 module_exit(my_radix_tree_exit);
 36 MODULE_LICENSE("GPL");

执行结果如下：

5. 参考文章

https://biscuitos.github.io/blog/RADIX-TREE/

http://blog.chinaunix.net/uid-20718037-id-5728709.html

https://ivanzz1001.github.io/records/post/data-structure/2018/11/18/ds-radix-tree