数据结构与算法（三）--栈

一、前言

前两篇文章我们学习了第一个数据结构，数组，且从底层通过java实现了数组的构建和增删改查的操作功能，并且通过resize操作使我们的数组可以动态的扩容或者缩容。且我们知道数组最大的优点就是在索引有语义的情况下，查询和修改操作会非常的快，反之我们就得遍历寻找元素。我们还了解了时间复杂度，渐进复杂度，分摊复杂度和复杂度震荡等知识，分析动态数组相关操作的时间复杂度并且优化了resize操作。那么从这一章我们要学习另一种线性数据结构-栈。

二、栈（Stack）

• 栈也是一种线性结构
• 相比数组，栈对应的操作是数组的子集
• 我们只能从一端添加元素，也只能从同一端取出元素
• 这一端我们称为栈顶

当我们这样限定我们的数组形成了栈这样一个数据结构之后，它却可以在我们计算机组成逻辑有着非常非常重要的作用。

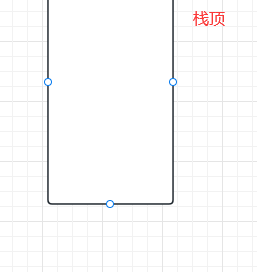
然后我们只能往栈顶这一端放入数据，这个放数据的过程通常我们称之为入栈：

需要注意的是，3只能放在2的上面，不能放在1和2的中间或者1的下面，这就是我们只能往栈顶这一端放入数据这个的体现。
如果我们现在想从栈取出元素，我们只能取出先取出3这个元素，因为3目前在栈顶，我们拿不到2和1，甚至从用户角度根本看不到2和1这两个元素。用户只能看到栈顶的元素，我们将元素从栈顶取出的过程叫作出栈。且出栈也体现了只能从同一端（栈顶）取出元素。

• 从放入和取出的过程我们可以看到，栈是一种后进先出的数据结构（LIFO-Last In First Out）。

我们从刚才的例子可以看到，3是我们最后放入栈的元素，但却是第一个从栈被取出的元素

三、栈的应用

1. 无处不在的undo操作（撤销）

原理就是栈的应用。
例如我现在在文本里输入“沉迷”，对于这个动作，我们编辑器就会记录下来，这个记录动作其实就是把动作放进栈中，然后打入“学习”，接着本来打入“无法自拔”结果打成了“不法自拔”，由于打错也算一个动作这个时候就会把这些入栈过程体现为：

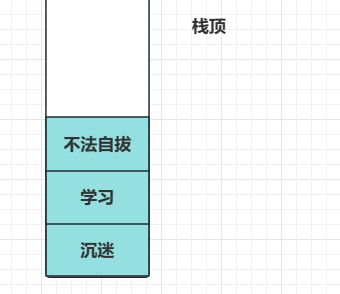
然后你意识到打错了，这个时候撤销，你执行撤销操作的过程就是从栈中拿出栈顶的元素，通过栈顶的元素来确认你最近的操作是什么，所以这次撤销操作就是把“不法自拔”从栈拿出然后删掉：

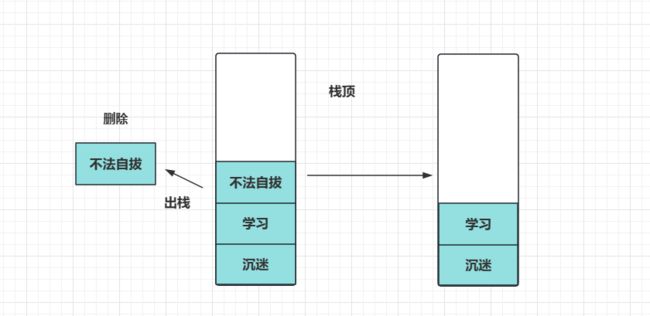
然后就可以继续重复之前的操作从而打入正确的文本。

2. 程序调用的系统栈
   事实上，在我们程序调用的过程中经常会出现在一个逻辑的中间先终止，然后跳到另外的逻辑去执行，例如子函数的调用，这个过程中计算机就需要使用一个系统栈，其实就是栈的数据结构来记录我们程序的调用过程。
   例如，下面有三个函数，其中A在第二行代码执行B()，B()在第二行代码执行C()，C()直接执行完普通的三行代码，没有子函数调用。那么对于我们计算机来说当执行A第二行代码的时候，此时程序暂时中断，转而去执行B函数，此时我们的系统栈就会记录一个信息叫作A2，代表之前这个程序执行到A的第二行了，这里进行了中断去执行B函数了；同理执行B第二行代码的时候，转而去执行C函数暂时中断B函数，系统栈会记录一个信息叫B2
   
   当C函数执行完了后，计算机就会遇到个问题，下面需要去执行什么，答案就是查看系统栈，对于系统栈来说，栈顶是B2，它就知道执行到B函数第二行的时候中断了，我就可以跳回到B2这个位置继续执行了，此时B2出系统栈并且删除，同理执行完B后看到系统栈还有A2，跳回到A2这个位置继续执行完整个程序。此时系统栈是空的，整个过程才算执行完毕。
   

这就是我们编程的时候进行子过程调用的时候，当一个子过程完成后可以自动的回到上层函数调用中断的位置，继续执行下去的原因，因为背后有一个系统栈，它可以记录每一次调用过程中中断的那个点。
基于这个原理的算法例如递归就是类似这样实现的。

四、栈的实现

上一节说了栈的定义和应用，其实大家会发现栈的应用非常重要，但是它实现起来其实非常简单，我们只需要实现以下方法即可：
Stack

• void push(E) 入栈
• E pop() 从栈中拿出元素，出栈
• E peek() 查看当前栈顶元素，也可以叫top()
• int gitSize() 查看栈里一共有多少元素
• boolean isEmpty() 查看栈是否为空

从用户的角度看，支持这些操作就好，和数组差不多，用户不想担心怎样resize的，他只需要知道数组是动态的，我可以通过数组添加删除元素是正常的就好了。对于栈亦是如此
对于具体底层实现，用户不关心，实际底层有多种实现方式，但是这里我们只采用基于动态数组的方式实现的栈。由于栈本身主要就是上面说的那5种操作，我们完全可以将Stack本身定义为一个接口，接口定义上面5个操作，然后写一个具体的实现类叫作ArrayStack通过数组的方式具体实现这5个操作。
ps:此次数组栈的实现方式需要前面文章动态数组的实现的基础，所以最好需要去查看动态数组的实现这篇博客，有了动态数组的实现基础，我们会发现数组栈的实现就非常简单：
1、首先我们需要编写Stack接口，定义5个基础操作，代码如下：

public interface Stack<T> {
	int getSize();
	boolean isEmpty();
	void push(T t);
	T pop();
	T peek();
}

2、编写ArrayStack类实现Stack接口，实现5个操作的方法，代码如下：

import com.mbw.array.DynamicArray;

public class ArrayStack<T> implements Stack<T> {
	private DynamicArray<T> dynamicArray;

	public ArrayStack(int capacity){
		this.dynamicArray = new DynamicArray<>(capacity);
	}

	public ArrayStack(){
		this.dynamicArray = new DynamicArray<>();
	}

	@Override
	public int getSize() {
		return dynamicArray.gitSize();
	}

	@Override
	public boolean isEmpty() {
		return dynamicArray.isEmpty();
	}

	@Override
	public void push(T t) {
		dynamicArray.addLast(t);
	}

	@Override
	public T pop() {
		return dynamicArray.removeLast();
	}

	@Override
	public T peek() {
		return dynamicArray.getLast();
	}

	@Override
	public String toString() {
		return "ArrayStack{" +
				"top = " + peek() +
				'}';
	}
}

其实这里说一下我一开始实现的误解的点，我认为栈顶等于数组第一个位置，所以我认为push和pop对应的不应该是addLast和removeLast,而是addFirst和removeFirst.peek也是getFirst()。但是这样说明我们对栈的定义是有错误的，其实我们只需要保证放入元素和去除元素是同一端即可，此时这个"同一端"不管是从数组头还是数组尾，其实都是可以的。那么我们当然选择addLast和removeLast啊，addFirst和removeFirst时间复杂度铁打的O(n)，而addLast和removeLast从均摊复杂度角度分析其实是O(1),效率更高。
然后我们可以试一下我们编写的栈：

public static void main(String[] args) {
		ArrayStack<String> stringArrayStack = new ArrayStack<>();
		stringArrayStack.push("沉迷");
		stringArrayStack.push("学习");
		stringArrayStack.push("不法");
		String pop = stringArrayStack.pop();
		System.out.println(pop);
		stringArrayStack.push("无法自拔");
		System.out.println(stringArrayStack.peek());
		System.out.println(stringArrayStack.toString());
	}

对于toString很多小伙伴可能会有疑惑为什么不把栈的所有元素打出来，其实从用户角度而言，栈这个数据结构用户只需关注栈顶的元素，我们从原则上也不应该把栈的中间元素给展示出来。不过自己学习的话可以将成员变量array的详情打印出来便于我们查看分析问题。这里就不做过多讲述。
而对于复杂度分析，除了之前说的push和pop从均摊复杂度角度分析都是O(1)，而peek()，getSize()，isEmpty()这几个操作很明显都是O(1)的，所以栈的性能是非常良好的。

五、栈的另一个应用–括号匹配（编译器）

想必很多干开发的朋友会很熟悉，例如我们编程的时候使用小括号，中括号的逻辑，或者我们写块逻辑，无论是for,if,while或者定义一个函数或者类都需要使用大括号，经常会有这种括号套括号的情况，在这种情况下，如果我们的括号匹配不成功的话，那我们的编译器就会报错，而这个原理就是应用栈。
本章我们会通过leetcode的一个题目通过编程的方式完成这个应用—20. 有效的括号
那么这题我们来看看如何通过栈来解决该问题：
首先假设字符串为([{}])
我们先从头开始，将字符串为左括号的入栈。如下图：

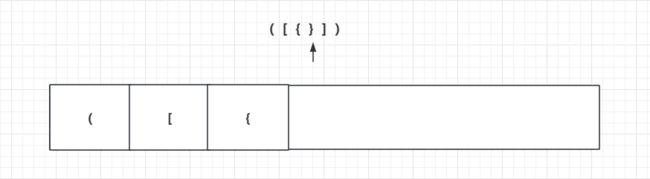
直到遍历字符串到第一个右括号的时候，这个时候出栈，将栈的第一个元素和当前字符做匹配，以此类推，如果最后都匹配上了，栈一定为空。如果栈不为空，说明有多的左括号。
而一旦没匹配上，则直接返回false。例如下图大括号和栈顶的中括号不匹配：

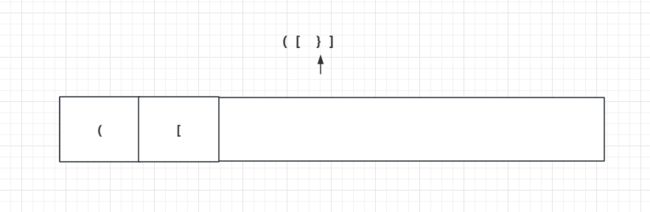
总结一句话就是：
栈顶元素反映了在嵌套的层次关系中，最近的需要匹配的元素
接着我们掌握了原理，就可以编程解决了，这里我们不使用我们自定义的ArrayStack解决，而是通过java.util.Stack解决，其实熟悉的小伙伴会发现我们自己编写的ArrayStack和Stack的方法是一致的。
那么逻辑如下

class Solution {
	public boolean isValid(String s) {
	    //如果字符串长度不是偶数，那么肯定不匹配，返回false
		if (s.length() % 2 == 1){
			return false;
		}
		Stack<Character> stack = new Stack<>();
		for (int i = 0; i < s.length(); i++) {
			char c = s.charAt(i);
			//如果是左括号则入栈
			if (c == '(' || c == '[' || c == '{') {
				stack.push(c);
			} else {
				//如果此时栈是空的，那么说明没有左括号只有右括号，那肯定是不匹配的，直接返回false
				if (stack.isEmpty()) {
					return false;
				}
				if (!validatePopAndChar(stack, c)) {
					return false;
				}
			}
		}
		//for循环结束后如果栈还有元素那么说明存在未匹配多余的左括号，返回false，否则返回true
		return stack.isEmpty();
	}

	private boolean validatePopAndChar(Stack<Character> stack, char c) {
	     //不是左括号，出栈和左括号匹配
		Character pop = stack.pop();
		if (c == ')' && pop != '(') {
			return false;
		}
		if (c == ']' && pop != '[') {
			return false;
		}
		return c != '}' || pop == '{';
	}
}

最后可以通过。