数据结构与算法——10.链表
这篇文章我们来讲一下数据结构与算法中的链表
目录
1.概述
2.单向链表的实现及其增删改查和遍历
3.带哨兵的单链表
4.带哨兵的双向链表
5.带哨兵的双向环形链表
6.反转单向链表
7.根据节点值来删除节点
8.删除单向链表倒数第n个节点
9.删除链表中的重复节点(保留一个)
10.删除链表中的所有重复节点(全删,不保留)
11.合并有序链表
12.找链表的中间节点
13.判断链表是否有环
14.总结
1.概述
定义:在计算机科学中,链表是数据元素的线性集合,其每个元素都指向下一个元素,元素存储上不连续
分类:根据链表的特性,我们可以将其分为单向链表、双向链表、循环链表
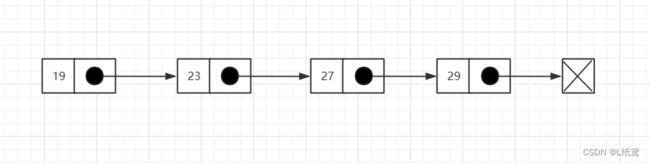
单向链表:只有一个数值域和一个指针域,每个元素只知道其下一个元素是谁,尾结点的指针域指向空
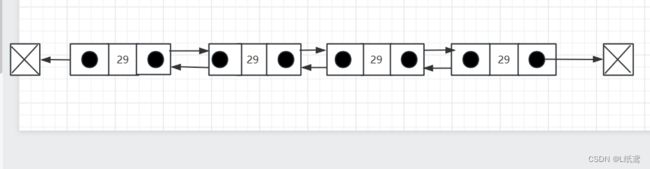
双向链表:有一个数值域和两个个指针域,每个元素知道其上一个和下一个元素是谁,头节点和尾结点的指针域指向空
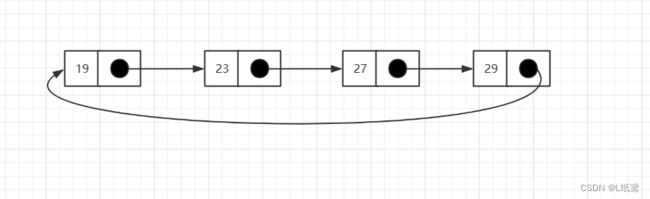
循环链表:通常的链表尾结点tail指向都是null,而循环链表的tail指向的是头结点head
注意:
链表内还有一种特殊的节点称为哨兵(Sentinel)节点,也叫做哑元(Dummy)节点,它不存储数据,通常用作头尾,用来简化边界的判断,如下图所示:
性能:
随机访问:根据index来查找,时间复杂度为O(n)
插入或删除:
- 起始位置:O(1)
- 结束位置:如果已知tail尾结点是O(1),不知tail尾结点是O(n)
- 中间位置:根据index查询时间+O(1)
2.单向链表的实现及其增删改查和遍历
首先,我们先思考如何实现,然后再用代码来实现。
我们知道,链表是由节点构成的,所以如果我们要创建链表就必须先创建节点(面向对象的思想),那我们就应该思考节点类的构成。节点有指针域和数值域,数值域很简单,就是存放数值的,指针域是指向下一节点的,而节点是类,是new出来的,要设一个变量来指向一个对象,那么这个变量的类型就一定是该类的类型,至此,节点类的属性就思考完了。下面再想一想节点类需要哪些方法,首先构造方法肯定要有,赋初值的嘛,get和set方法需要吗?不需要,因为get和set方法是获取和设置节点值的,而这个功能我们需要在链表中完成,所以节点类不需要这些方法。因为节点和链表是组成的关系,所以节点类是链表类的内部类,并且要对外隐藏。至此,节点类我们思考完毕了。
下面,我们来思考链表。你要指向下一个节点,就肯定需要一个地方来存储下一节点的位置,所以头结点就需要了,所以链表里面首先应该设置头结点。
有了头结点,下面来想一想链表类中应该有哪些方法,毫无疑问增删改查是需要的,插入也是需要的。增加,怎么增加?是从前面增加还是后面增加?很复杂,咱一点点分析。
首先,你只有头结点,没有其他节点,所以你需要一个方法来插入节点,这个方法是直接添加的head头结点后面的,可以理解为头插法。方法需要什么?需要数值,即你需要插入的值,所以形参为一个int类型的变量;方法需要返回什么?不需要返回什么,所以类型为void,至此方法框架出来了,我们将其命名为addFirst。然后再思考其功能的实现。如果一开始,头结点后面没有节点,那就简单了, 你直接new一个节点处理,节点构造函数的数值域就用形参来填充,指针域怎么办?因为你只插入这一个,所以这个节点后面没有内容,所以指针域我们可以设置为空。谁指向这个节点?头指针!怎么做?将这个对象赋值给头结点就可以了,因为头结点就是节点类型的对象。如果一开始,头结点后面有节点,那么我们应该怎么做才能在头结点后面插入元素?很简单,还先new一个节点出来,依然将此节点赋值给head节点,数值域依然是形参变量,指针域怎么办?这个节点要指向哪里?这个节点要指向头结点原先指向的节点。那头结点原先指向的节点的地址在哪存储着?在头结点中存储着,所以新节点的指针域的值就是原先头结点的值。(说实话,这里有点绕,但是很好理解)回过头我们再思考这个方法中的内容,其实第一行代码是可以省略的,因为如果头结点一开始有内容,那很好,新节点的指针域的值为头节点的值,如果头结点一开始为空,那新节点的指针域的值为头节点的值即为空。
下面来想一想尾插法如何实现,即如何实现在尾部插入节点。要在尾部插入节点,首先应该知道尾结点是哪一个,我们链表中只记录了头结点,没记录尾结点,所以我们首先应该遍历这个链表
下面来看一下如何遍历链表,其实很简单,一个while循环就解决了,什么时候跳出循环?当某个节点的指针域为空的时候就跳出循环。当然遍历链表不一定是打印,所以方法不应该写死。有很多种遍历方法,具体实现的时候会展示的,这里就不多赘述了
下面说一个小问题,我们的节点类是定义在类的内部的,为什么要加static?这里只说一点原因,因为我们的链表是节点组成的,是先有节点再有链表的。static表示静态,它修饰的元素是在类的加载的时候就会实例化,而不加static的元素是在对象创建的时候再实例化的,我们需要节点在实例化在链表的实例化之前实现,所以要加static。
现在在来看一下尾插法,要实现尾插法,首先我们需要找到尾结点,这个逻辑和遍历的逻辑类型,最后只需要返回一个节点就行。此时,就很简单了,新节点的指针域为形参,指针域为空,并且原先的尾结点指向这个新节点。
下面看一下如何根据索引来找到节点中的值。先说明一下,链表中是没有索引的,如果给节点再加一个索引域,那么链表维护起来会超级复杂。因为如果我随便删掉中间的一个节点,那么后续节点的索引都要改变,很麻烦。所以根据索引来查找节点中的值,首先我们应该找到该节点的索引,怎么找?用遍历的方法找,就是一个循环+一个if判断就解决的事,找到索引了然后就根据索引用一个循环就找到了这个索引的节点,然后就找到了这个节点的值。
下面看一下如何在两个节点中间插入一个节点。我们需要传入插入的位置和插入的值,插入的位置即该节点的索引,所以我们还有找到该索引的前一个节点,这就需要用到我们前面的方法了。现在找到了插入位置的前一个索引,我们需要先创建一个节点,这个节点的指针域就是其前一个节点的指针域的值,而这个节点的前一个节点的指针域就要指向这个节点,这样就插入成功了。其实逻辑很简单。
下面讲一下删除节点。先说一下如何删除第一个节点,即头删法。很简单,头结点指向被删除节点的下一个节点,就这。那如何按照索引来删除节点呢?也很简单,先找到索引位置的上一个节点,然后根据这个节点找到被删除的节点,然后让被删除节点的上一个节点的指针域等于被删除节点的指针域。
至此,关于链表的一些简单操作就讲解完毕了,下面来看一下代码实现(代码中有些细节可能考虑不周到)
下面给出具体的代码:
import java.util.Iterator;
import java.util.function.Consumer;
/**
* 无哨兵的单向链表
* */
public class L3_SinglyLinkedList implements Iterable {
//定义头结点,并设初值为空
private Node head = null;
//节点类,设为静态的
private static class Node{
int value;//值
Node next;//指向下一个节点
//节点类的构造函数,赋值用的
public Node(int value, Node next) {
this.value = value;
this.next = next;
}
}
//头插法
public void addFirst(int value){
//1.链表为空
//head = new Node(value,null);
//2.链表非空
head = new Node(value,head);
}
//while循环写死的遍历
public void loop1(){
//定义一个节点来循环遍历链表
Node p = head;
//当节点不为空的时候,说明它后面还有节点,所以要继续遍历
while (p != null){
//写死的,打印输出
System.out.println(p.value);
//节点后移
p = p.next;
}
}
//for循环写死的遍历
public void loop2(){
//这个for循环的条件值得看一下
for(Node p = head; p != null; p = p.next){
System.out.println(p.value);
}
}
//用函数式接口写的遍历
public void loop3(Consumer consumer){
for(Node p = head; p != null; p = p.next){
//用consumer来接收节点的值
consumer.accept(p.value);
}
}
//迭代器式遍历
@Override
public Iterator iterator() {
return new Iterator() {
Node p = head;
@Override
public boolean hasNext() {//是否有下一个元素
return p != null;
}
@Override
public Integer next() {//返回当前的元素并指向下一个元素
int v= p.value;
p = p.next;
return v;
}
};
}
//寻找最后一个节点
private Node findLast(){
//如果一开始就没有,那就直接返回null了
if (head == null)
return null;
//定义变量,来遍历节点,并让其停留在尾结点的位置,并返回它
Node p ;
//用循环来往后遍历
for (p = head;p.next != null; p = p.next){
}
return p;
}
//尾插法
public void addLast(int value){
//获取尾结点
Node last = findLast();
//如果尾结点为空,即链表中没有节点,那就使用头插法
if (last == null){
addFirst(value);
return;
}
//尾插
last.next = new Node(value,null);
}
//返回节点的索引
private Node findNode (int index){
//第一索引变量,初始值设为0
int i = 0;
for (Node p = head; p != null; p = p.next,i++){
if(i == index){
return p;
}
}
return null;
}
//获取索引处节点的值
public int get(int index){
//首先,获取索引出的节点
Node node = findNode(index);
//判断索引处的节点是否为空,如果为空,说明索引有问题,抛异常
if (node == null){
throw IllegalIndex(index);
}
return node.value;
}
//抛出的异常方法
private IllegalArgumentException IllegalIndex(int index) {
return new IllegalArgumentException(String.format("index[%d] 不合法%n", index));
}
//随机插入
public void insert(int index,int value){
//首先判断索引是否为0,如果为0,说明链表中没有节点,那么就用头插法插入
if(index == 0){
addFirst(value);
return;
}
//找到目标索引的前一个节点
Node prev = findNode(index-1);
//判断索引的前一个节点是否为空,如果索引的前一个节点为空,说明索引错误(比如2个节点的链表,你给了索引10,那当然错误)
if (prev == null){
//抛异常
throw IllegalIndex(index);
}
//索引的前一个的节点的指针域指向新节点,新节点的指针域等于索引前一个节点的指针域的值
prev.next = new Node(value,prev.next);
}
//头删法
public void removeFirst(){
//判断索引头节点是否为空,为空说明这是空链表,就抛异常
if (head == null)
throw IllegalIndex(0);
//不为空,就让头节点的指针域等于头结点的指针域的下一个的下一个的节点的位置
head = head.next;
}
//根据索引来删除
public void remove(int index){
//判断索引是否为0,如果为0,那就说明要删第一个节点,就用头删法来删
if (index == 0){
removeFirst();
return;
}
//找到被删除节点的前一个节点
Node prev = findNode(index-1);
//如果被删除节点的前一个节点为空,那说明索引出问题了,就抛异常
if (prev == null){
throw IllegalIndex(index);
}
//找到被删除的节点
Node removed = prev.next;
//判断被删除的节点是否为空,如果为空就抛异常(比如有3个节点,我给个索引3,那么被删除的节点就是空)
if (removed == null){
throw IllegalIndex(index);
}
//被删除节点的前一个节点的指针域等于本删除节点的指针域
prev.next = removed.next;
}
}
3.带哨兵的单链表
前面粗浅的讲了一下哨兵是啥,这里再详细说一下。可以这样说,哨兵是一个我们只关心其指针域不关心其数值域的节点。在实现不带哨兵节点的链表时,我们的许多方法中都是要判断头结点是否为空,即head节点是否为空,如果为空是一种做法,不为空是另一种做法,但是有了哨兵节点后,我们就不用再关注头结点了,因为哨兵节点一定不为空并且哨兵节点一定存在。这样,我们的链表实现方法就可以简单很多了。
下面只给出带哨兵的链表的创建,链表中的具体方法就不写了,大家自己思考着改动(改动不大)
注意:我们一开始写的时候,head是没有对象的,head没有new对象出来,所以head不是实际的节点,而这里是直接new出来了,即new出一个对象了,这时head就指向了这样的一个节点,这就是哨兵节点,而前面的就不是哨兵节点。
4.带哨兵的双向链表
下面,我们来看一下带哨兵的双向链表。分析思路和前面的单向链表相似,方法的实现思路也大差不差,所以这里就不再详细讲解了,直接看代码吧,代码里会有详细的注释的。
具体代码如下:
import java.util.Iterator;
/**
* 带哨兵的双向链表
* */
public class L4_DoublyLinkedListSentinel implements Iterable {
//节点类,有头,有尾,有值,有构造函数
private static class Node{
Node prev;
int value;
Node next;
//节点类的构造函数
public Node(Node prev, int value, Node next) {
this.prev = prev;
this.value = value;
this.next = next;
}
}
private Node head; //头指针域
private Node tail; //尾指针域
//双向链表的构造函数
public L4_DoublyLinkedListSentinel() {
head = new Node(null,111,null);
tail = new Node(null,222,null);
head.next = tail;
tail.next = head;
}
//抛出的异常方法
private IllegalArgumentException IllegalIndex(int index) {
return new IllegalArgumentException(String.format("index[%d] 不合法%n", index));
}
//根据索引查找节点,就是要找到索引处的节点,肯定要用到遍历
private Node findNode(int index){
int i = -1;
for (Node p = head; p!= tail; p = p.next,i++){
if (i == index)
return p;
}
return null;
}
//从头部加入元素
public void addFirst(int value){
//就是从0处插入元素
insert(0,value);
}
//从头部删除元素
public void removeFirst(){
//就是从0处删除元素
remove(0);
}
//从尾部加入元素
public void addLast(int value){
/** //思路1,我的思路是找到尾部的位置,然后用插入方法来插入元素
int i = -1;
for (Node p = head; p!=tail; p=p.next,i++) {
}
insert(i,value);
*/
//思路2,双向链表的头尾位置是确定的
Node last = tail.prev;
Node added = new Node(last,value,tail);
last.next = added;
tail.prev = added;
}
//从尾部删除元素
public void removeLast(){
/** 思路1,和上面一样
* int i = 0;
for (Node p = head.next; p != tail; p=p.next,i++) {
}
remove(i-1);
*/
//思路2
Node removed = tail.prev;
if (removed == head){
throw IllegalIndex(0);
}
Node left = removed.prev;
tail.prev = left;
left.next = tail;
}
//插入元素
public void insert(int index,int value){
//找到插入位置的前一个节点
Node left = findNode(index-1);
//前一个节点为空,说明此节点为头结点即头哨兵
if (left == null){
throw IllegalIndex(index);
}
//找到插入位置的后一个节点
Node right = left.next;
//构造新的节点
Node p = new Node(left,value,right);
//改变指向
left.next = p;
right.prev = p;
}
//删除元素
public void remove(int index){
//找到删除位置的前一个节点
Node left = findNode(index-1);
//同上面插入的原理一样
if (left == null){
throw IllegalIndex(index);
}
Node p = findNode(index);
if (p == tail){
throw IllegalIndex(index);
}
Node right = p.next;
left.next = right;
right.prev = p.prev;
}
public void show1(){
for (Node p = head.next; p != tail ; p=p.next) {
System.out.println(p.value);
}
}
//遍历
@Override
public Iterator iterator() {
return new Iterator() {
Node p = head.next;
@Override
public boolean hasNext() {
return p!=tail;
}
@Override
public Object next() {
int value = p.value;
p = p.next;
return value;
}
};
}
}
5.带哨兵的双向环形链表
带哨兵的双向环形链表就意味着这个哨兵即使头也是尾,最后一个元素也指向此哨兵
大致思路和上面的差不多,不细讲,直接看一下代码,代码中有具体的注释
import java.util.Iterator;
/**
* 带哨兵的双向环形链表
* */
public class L5_DoublyAnnularLinkListSen implements Iterable {
//先定义节点类
private static class Node{
Node prev;
int value;
Node next;
//构造函数,给节点赋初值的
public Node(Node prev, int value, Node next){
this.prev = prev;
this.value = value;
this.next = next;
}
}
//定义哨兵
Node sentinel;
public L5_DoublyAnnularLinkListSen(){
sentinel = new Node(null,666,null);
//构成环,没元素的时候都指向自己
sentinel.prev = sentinel;
sentinel.next = sentinel;
}
//抛出的异常方法
private IllegalArgumentException IllegalIndex(int index) {
return new IllegalArgumentException(String.format("index[%d] 不合法%n", index));
}
//根据索引查找节点,就是要找到索引处的节点,肯定要用到遍历(这个方法有点问题)
/*private Node findNode(int index){
Node p = sentinel;
for (int i = -1 ; p.next !=sentinel ; p=p.next,i++ ){
if (i == index)
return p;
}
return null;
}*/
//从头部加入元素
public void addFirst(int value){
//insert(0,value);//自己的思路,但是有点问题,只有哨兵节点时插入失败
//确定插入位置的前一个和后一个节点
Node a = sentinel;
Node b = sentinel.next;
//构造插入节点
Node added = new Node(a,value,b);
a.next = added;
b.prev = added;
}
//从头部删除元素
public void removeFirst(){
//被删除的节点
Node removed = sentinel.next;
if (removed == sentinel)
throw new IllegalArgumentException("非法");
//被删除的节点的前一个节点
Node a = sentinel;
//被删除的节点的后一个节点
Node b = removed.next;
a.next = b;
b.prev = a;
}
//从尾部加入元素
public void addLast(int value){
//插入处的前一个节点
Node a = sentinel.prev;
//插入处的后一个节点
Node b = sentinel;
Node added = new Node(a,value,b);
a.next = added;
b.prev = added;
}
//从尾部删除元素
public void removeLast(){
Node removed = sentinel.prev;
if (removed == sentinel)
throw new IllegalArgumentException("非法");
Node a = removed.prev;
Node b = sentinel;
a.next = b;
b.prev = a;
}
//插入元素,根据索引插入元素,这个有点问题
/*public void insert(int index,int value){
Node left = findNode(index-1);
if (left == null)
throw IllegalIndex(index);
Node right = left.next;
Node added = new Node(left,value,right);
left.next = added;
right.prev = added;
}*/
//根据节点的值删除元素
public void remove(int value){
Node removed = findByValue(value);
if (removed == null)
return;
Node a = removed.prev;
Node b = removed.next;
a.next = b;
b.prev = a;
}
//根据值来查找节点
private Node findByValue(int value){
/* for (Node p = sentinel.next;p.value == value;p=p.next)
return p;*/
//另一个逻辑
Node p = sentinel.next;
while (p != sentinel){
if (p.value == value){
return p;
}
p = p.next;
}
return null;
}
//打印输出
public void show1(){
for (Node p = sentinel.next; p!=sentinel; p=p.next ) {
System.out.println(p.value);
}
}
//遍历
@Override
public Iterator iterator() {
return new Iterator() {
Node p = sentinel.next;
@Override
public boolean hasNext() {
return p != sentinel;
}
@Override
public Object next() {
int value = p.value;
p = p.next;
return value;
}
};
}
}
6.反转单向链表
下面来看一下单向链表的反转,一共介绍了5中解决方法:
总结:一个核心思想:把后面的往前面放;理解掌握四项内容:头插,尾插,赋值,指向
7.根据节点值来删除节点
下面来看一下如何根据节点的值来删除节点:
总结:这个操作主要就是在考如何删除节点,一般是用双指针法
8.删除单向链表倒数第n个节点
下面来看一下如何删除单向链表的倒数第n个节点:
9.删除链表中的重复节点(保留一个)
下面来看一下如何删除链表中的重复节点:
10.删除链表中的所有重复节点(全删,不保留)
下面来看一下如何删除链表中的全部重复节点:
11.合并有序链表
下面来看一下如何合并有序链表:
12.找链表的中间节点
下面看一下如何找链表的中间节点:
13.判断链表是否有环
下面看一下如何判断链表是否有环:
14.总结
对于链表,我们要掌握其数据结构,熟练掌握其增删改查与遍历。包括头插、尾插、中间插、头删、尾删、中间删、根据值来索引,遍历等基本操作,除此之外还包括:反转、合并、删除倒数第n个、去重、判断是否有环等操作,这些都要掌握,后面的那些主要是掌握其解题方法。
对于链表我们要理解:赋地址,指向,指针等相互含义,知道每个操作语句的具体含义是啥,这里特别容易弄混。还要知道什么时候是指向,什么时候是头结点,递归之后返回什么都要明白。
在单链表的基础上,我们又学习了带哨兵单链表,带哨兵双向链表,环形链表。其实后面的这些链表的操作比但链表都要简单。
除此之外我们还学习了递归。对于递归我们要知道:返回了什么,传递了什么,什么时候结束,变量是什么,一般我们要从开始,中间,最后这三个过程来分析一个递归问题。
暂时就这么多,大家有什么好的想法可以友善交流。
最后附上练习的源码,供大家参考(有些方法没有测试):
package LeetBook;
/**
* 这个类主要写链表的一些操作
* 链表问题的注意点:
* 头结点,节点的地址存储在哪,节点指向哪,节点类型的变量的含义
*
* */
public class L7_LinkedListPractice {
//节点类
private static class ListNode{
//属性
public int val;
public ListNode next;
//三个构造方法
public ListNode() {}
//这就是默认指向空了
public ListNode(int val) {
this.val = val;
}
public ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
//打印输出函数
@Override
public String toString(){
StringBuilder sb = new StringBuilder(64);
sb.append("[");
//指向自己,this的意义就是类(对象)自己
ListNode p = this;
while (p!=null){
sb.append(p.val);
if (p.next != null){
sb.append(",");
}
p = p.next;
}
sb.append("]");
return sb.toString();
}
}
//主函数
public static void main(String[] args) {
//这里主要测试了一些方法,当然有些还没有测试
ListNode o5 = new ListNode(5);
ListNode o4 = new ListNode(4,o5);
ListNode o3 = new ListNode(3,o4);
ListNode o2 = new ListNode(2,o3);
ListNode o1 = new ListNode(1,o2);
ListNode a4 = new ListNode(14);
ListNode a3 = new ListNode(13,a4);
ListNode a2 = new ListNode(12,a3);
ListNode a1 = new ListNode(11,a2);
ListNode b4 = new ListNode(11);
ListNode b3 = new ListNode(5,b4);
ListNode b2 = new ListNode(4,b3);
ListNode b1 = new ListNode(1,b2);
// System.out.println(o1);
//
// ListNode n1 = removeListNode1(o1,3);
// System.out.println(n1);
// ListNode[] lists = {o1,a1,b1};
// ListNode m = new L7_LinkedListPractice().mergeLists(lists);
// System.out.println(m);
Boolean a = new L7_LinkedListPractice().isPalindrome(o1);
System.out.println(a);
}
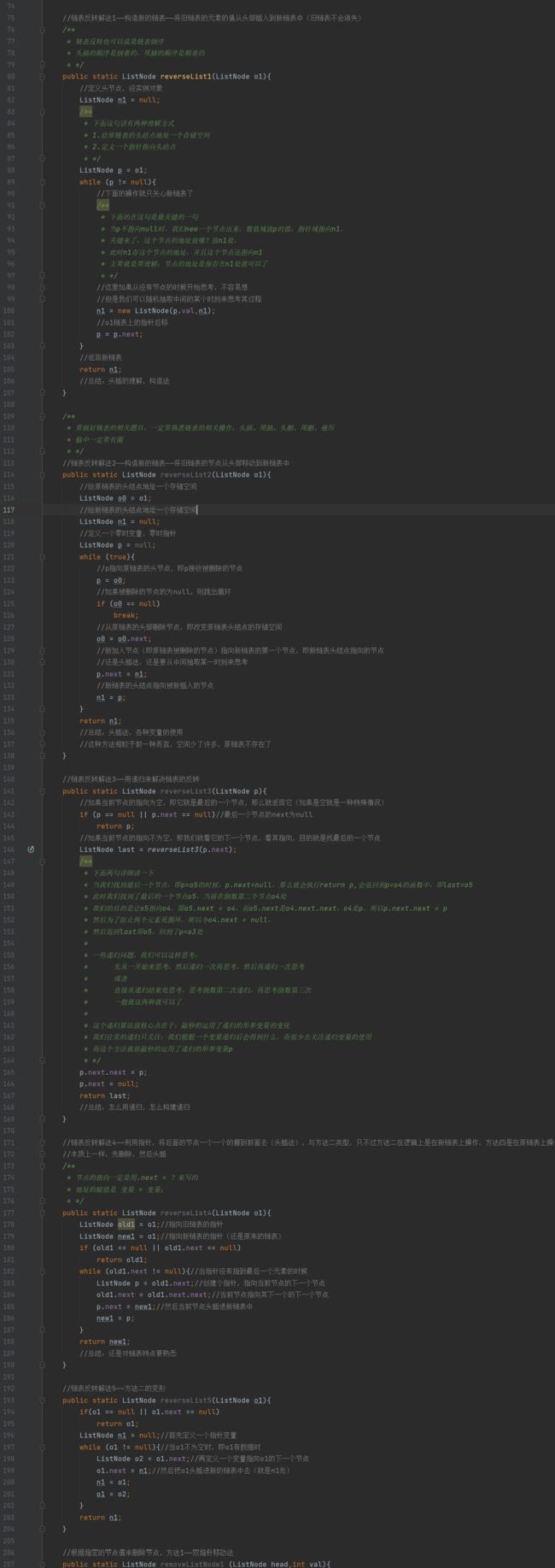
//链表反转解法1——构造新的链表——将旧链表的元素的值从头部插入到新链表中(旧链表不会消失)
/**
* 链表反转也可以说是链表倒序
* 头插的顺序是倒着的,尾插的顺序是顺着的
* */
public static ListNode reverseList1(ListNode o1){
//定义头节点,没实例对象
ListNode n1 = null;
/**
* 下面这句话有两种理解方式
* 1.给原链表的头结点地址一个存储空间
* 2.定义一个指针指向头结点
* */
ListNode p = o1;
while (p != null){
//下面的操作就只关心新链表了
/**
* 下面的在这句是最关键的一句
* 当p不指向null时,我们new一个节点出来,数值域放p的值,指针域指向n1,
* 关键来了,这个节点的地址放哪?放n1处,
* 此时n1存这个节点的地址,并且这个节点还指向n1
* 主要就是要理解:节点的地址是保存在n1处就可以了
* */
//这里如果从没有节点的时候开始思考,不容易想
//但是我们可以随机抽取中间的某个时刻来思考其过程
n1 = new ListNode(p.val,n1);
//o1链表上的指针后移
p = p.next;
}
//返回新链表
return n1;
//总结:头插的理解,构造法
}
/**
* 要做好链表的相关题目,一定要熟悉链表的相关操作,头插、尾插、头删、尾删、遍历
* 脑中一定要有图
* */
//链表反转解法2——构造新的链表——将旧链表的节点从头部移动到新链表中
public static ListNode reverseList2(ListNode o1){
//给原链表的头结点地址一个存储空间
ListNode o0 = o1;
//给新链表的头结点地址一个存储空间
ListNode n1 = null;
//定义一个零时变量,零时指针
ListNode p = null;
while (true){
//p指向原链表的头节点,即p接收被删除的节点
p = o0;
//如果被删除的节点的为null,则跳出循环
if (o0 == null)
break;
//从原链表的头部删除节点,即改变原链表头结点的存储空间
o0 = o0.next;
//新加入节点(即原链表被删除的节点)指向新链表的第一个节点,即新链表头结点指向的节点
//还是头插法,还是要从中间抽取某一时刻来思考
p.next = n1;
//新链表的头结点指向被新插入的节点
n1 = p;
}
return n1;
//总结:头插法,各种变量的使用
//这种方法相较于前一种而言,空间少了许多,原链表不存在了
}
//链表反转解法3——用递归来解决链表的反转
public static ListNode reverseList3(ListNode p){
//如果当前节点的指向为空,即它就是最后的一个节点,那么就返回它(如果是空就是一种特殊情况)
if (p == null || p.next == null)//最后一个节点的next为null
return p;
//如果当前节点的指向不为空,那我们就看它的下一个节点,看其指向,目的就是找最后的一个节点
ListNode last = reverseList3(p.next);
/**
* 下面两句详细讲一下
* 当我们找到最后一个节点,即p=o5的时候,p.next=null,那么就会执行return p,会返回到p=o4的函数中,即last=o5
* 此时我们找到了最后的一个节点o5,当前在倒数第二个节点o4处
* 我们的目的是让o5指向o4,即o5.next = o4,而o5.next是o4.next.next,o4是p,所以p.next.next = p
* 然后为了防止两个元素死循环,所以令o4.next = null,
* 然后返回last即o5,回到了p=o3处
*
* 一些递归问题,我们可以这样思考:
* 先从一开始来思考,然后递归一次再思考,然后再递归一次思考
* 或者
* 直接从递归结束处思考,思考倒数第二次递归,再思考倒数第三次
* 一般就这两种就可以了
*
* 这个递归算法放核心点在于:敲秒的运用了递归的形参变量的变化
* 我们往常的递归只关注:我们根据一个变量递归后会得到什么,而很少去关注递归变量的使用
* 而这个方法就很敲秒的运用了递归的形参变量p
* */
p.next.next = p;
p.next = null;
return last;
//总结:怎么用递归,怎么构建递归
}
//链表反转解法4——利用指针,将后面的节点一个一个的挪到前面去(头插法),与方法二类型,只不过方法二在逻辑上是在新链表上操作,方法四是在原链表上操作
//本质上一样,先删除,然后头插
/**
* 节点的指向一定是用.next = ?来写的
* 地址的赋值是 变量 = 变量;
* */
public static ListNode reverseList4(ListNode o1){
ListNode old1 = o1;//指向旧链表的指针
ListNode new1 = o1;//指向新链表的指针(还是原来的链表)
if (old1 == null || old1.next == null)
return old1;
while (old1.next != null){//当指针没有指到最后一个元素的时候
ListNode p = old1.next;//创建个指针,指向当前节点的下一个节点
old1.next = old1.next.next;//当前节点指向其下一个的下一个节点
p.next = new1;//然后当前节点头插进新链表中
new1 = p;
}
return new1;
//总结:还是对链表特点要熟悉
}
//链表反转解法5——方法二的变形
public static ListNode reverseList5(ListNode o1){
if(o1 == null || o1.next == null)
return o1;
ListNode n1 = null;//首先定义一个指针变量
while (o1 != null){//当o1不为空时,即o1有数据时
ListNode o2 = o1.next;//再定义一个变量指向o1的下一个节点
o1.next = n1;//然后把o1头插进新的链表中去(就是n1处)
n1 = o1;
o1 = o2;
}
return n1;
}
//根据指定的节点值来删除节点,方法1——双指针移动法
public static ListNode removeListNode1 (ListNode head,int val){
ListNode s = new ListNode(-1,head);//这才是名副其实的头结点,是真正的new出一个节点来了,是真实存在的一个节点,没有new的都不是头结点
ListNode p1 = s; //定义一个指针指向头结点
ListNode p2 = s.next; //定义一个指针指向第一个数值结点
while (p2 != null){//如果当前节点不为空,即存在
if (p2.val == val){//判断当前节点的值是否与目标值相等
p1.next = p2.next;//删除当前节点
p2 = p2.next;//指针后移一位
//p2 = p1.next //可以替换上一行
}else{
p1 = p1.next;//如果不相等,两个指针皆后移一位
p2 = p2.next;
//p2 = p1.next //可以替换上一行
}
}
return s.next;//返回第一个数值节点
}
//根据指定的节点值来删除节点,方法2——递归法
public ListNode removeListNode2 (ListNode p,int val){
if (p == null)
return null;
if (p.val == val)
return removeListNode2(p.next,val);//如果满足条件,就不返回当前节点,返回的是当前节点的下一个节点
else {
p.next = removeListNode2(p.next, val);//如果不满足条件,就返回当前节点,意思就是当前节点的下一个节点就是要返回的节点
return p;
}
//递归要清楚返回的是什么,是什么含义,实际代表什么,用什么来接收,
}
//删除链表的倒数第n个节点,方法1——递归法
public ListNode removeNthFromEnd1(ListNode head,int n){
ListNode s = new ListNode(-1,head);
recursion(s,n);//为啥用头结点做入参,不是很清楚,可以尝试一下用第一个节点做入参
return s.next;
}
public int recursion(ListNode p,int n){//这个递归的意义是递归出倒数第n个节点,并且删除
if (p == null)//如果递归到空节点了,就返回0,因为尾节点是第一个节点
return 0;
int nth = recursion(p.next,n);//然后就是用一个变量来接收返回的值,其实后面可以加一句:nth++,然后返回nth的,意思是一样的
if (nth == n){//找到倒数第n个了,那就删除这个节点,删除逻辑很简单
p.next = p.next.next;
}
return nth+1;
}
//删除链表的倒数第n个节点,方法2——双指针法
public ListNode removeNthFromEnd2(ListNode head,int n){
ListNode s = new ListNode(-1,head);//定义头结点
ListNode p1 = s;//定义两个指针,都指向头结点
ListNode p2 = s;
for (int i = 0; i <=n ; i++) {//让p2移动到第n+1个节点处(此时p1和p2间的距离为n+1)
p2 = p2.next;
}
while (p2 != null){//p2没移动到最后一个节点的时候,两个指针都往后移,
// 当p2指向最后一个节点的时候,两个指针都停止,此时两个指针间距离为n+1
p1 = p1.next;
p2 = p2.next;
}
p1.next = p1.next.next;//删除p1的下一个节点,即倒数第n个节点
return s.next;
//总结:对于链表的一些操作,双指针是常用的一种操作,就是要从题目中挖掘信息
//找出已知条件,挖掘隐藏条件(这个通常与题目中所述的数据结构和特性有关),然后找二者和问题间的关系
}
//删除有序链表中的重复节点(保留一个),方法1——双指针法
public ListNode deleteDuplicates1(ListNode head){
if (head == null || head.next == null)//为空或者只有一个节点就直接返回
return head;
ListNode p1 = head;//定义两个指针指向头
ListNode p2;
while ((p2 = p1.next) != null){//p2在前面,当p2不为null时
if (p1.val == p2.val){//值相等,删除p2
p1.next = p2.next;
}else {
p1 = p1.next;//不相等,就后移
}
}
return head;
//while的判断条件及其巧妙,p2永远在p1前一个,并且p2跟随p1变化
}
//删除有序链表中的重复节点(保留一个),方法2——递归法
public ListNode deleteDuplicates2(ListNode p){
if(p == null || p.next == null){
return p;
}
if (p.val == p.next.val){//值相等就返回下一个节点,不返回当前节点
return deleteDuplicates2(p.next);
}else {
p.next = deleteDuplicates2(p.next);//值不等就继续递归
return p;//这里有点迷糊!!!
}
}
//删除有序链表中的重复节点(删除所有),方法1——递归法
public ListNode deleteAllDuplicates1(ListNode p){
if (p == null || p.next == null){//为空或者只有一个节点,返回当前的节点
return p;
}
if (p.val == p.next.val){//值相等就跳过当前节点,
ListNode x = p.next.next;
while (x != null && x.val == p.val){//这就是不断的找相同的元素
x = x.next;
}
return deleteAllDuplicates1(x);//向上返回第一个非重复的节点
} else {
p.next = deleteAllDuplicates1(p.next);//如果不值相等,那么p就指向下一次递归返回的节点
return p;
}
//递归的返回是向上一层返回的,是向前返回的
}
//删除有序链表中的重复节点(删除所有),方法2——三指针法
public ListNode deleteAllDuplicates2(ListNode head){
if (head == null || head.next == null) //为空或者只有一个节点,返回当前的节点
return head;
ListNode s = new ListNode(-1,head);//定义头结点
ListNode p1 = s;//指向头结点的指针
ListNode p2,p3;//再定义两个指针
while( (p2 = p1.next) != null && (p3 = p2.next)!=null ){
//如果第一个和第二个节点不为空
if (p2.val == p3.val){
while ((p3 = p3.next) != null && p3.val == p2.val){}//值相等的时候,不停的后移p3
p1.next = p3;//删除那一大串,更改头节点
}else {
p1 = p1.next;//p2和p3是根据p1来改变的
}
}
return s.next;//返回第一个节点
}
//合并有序链表,方法1——创建新链表比较合并
public ListNode mergeTwoLists1(ListNode p1,ListNode p2){
ListNode s = new ListNode(-1,null);//创建头结点
//指向新链表的指针
ListNode p = s;
while (p1 != null && p2 != null){//当两个指针都不为空的时候进入循环
if (p1.val <= p2.val){//比大小,尾插,后移
p.next = p1;
p1 = p1.next;
//p也要向后移动一位
p = p.next;
}else {
p.next = p2;
p2 = p2.next;
p = p.next;
}
}
if (p1 != null)//对剩余元素的处理
p.next = p1;
if (p2 != null)
p.next = p2;
return s.next;
}
//合并有序链表,方法2——用递归的方法
public ListNode mergeTwoLists2(ListNode p1,ListNode p2){
if (p1 == null){//对剩余元素的处理
return p2;
}else if(p2 == null){
return p1;
}
if(p1.val < p2.val){//这里直接改变指向,没创建新链表
p1.next = mergeTwoLists2(p1.next,p2);
return p1;
}else {
p2.next = mergeTwoLists2(p1,p2.next);
return p2;
}
}
//合并多个升序链表
public ListNode mergeLists(ListNode[] lists){
if (lists.length == 0){
return null;
}
return split(lists,0, lists.length-1);
}
//返回合并后的链表,j,i代表左右边界
//分而治之:分、治、合(分而治之和递归一般要联系在一起,多路递归和分治是一样的)
//减而治之:不是分成多部分,而是减小问题规模来解决(就是单路递归,典型的就是递归实现二分查找)
//这个和归并排序是一样的思想
private ListNode split(ListNode[] lists,int i,int j){
if (i == j){
return lists[i];
}
int m = (i+j) >>> 1;
ListNode left = split(lists, i, m);
ListNode right = split(lists, m + 1, j);
return mergeTwoLists1(left,right);
}
//查找链表的中间节点——快慢双指针法
public ListNode findMid(ListNode head){//一个走一步,一个走两步,两步走到头,一步的到中间
ListNode p1 = head;
ListNode p2 = head;
while (p2 != null && p2.next != null){
p1 = p1.next;
p2 = p2.next;
p2 = p2.next;
}
return p1;
}
//判断一个链表是否是回文链表(回文:即正反读都是一样的)
public boolean isPalindrome(ListNode h1){
ListNode h2 = reverseList1(h1);//反转一下链表
for (;h1.next!=null;h1 = h1.next,h1 = h1.next){
if (h1.val != h2.val){
return false;
}
}
return true;
}
//判断链表是否有环——快慢指针法
//很简单的道理,如果有环,快的迟早追上慢的
public boolean hasCycle(ListNode head){
ListNode p1 = head;
ListNode p2 = head;
while (p1 != null && p2.next != null){
p1 = p1.next;
p2 = p2.next.next;
if ( p1 == p2){
return true;
}
}
return false;
}
//判断链表是否有环,如果有就返回环的入口
public ListNode hasCycle2(ListNode head){
ListNode h = head; //兔
ListNode t = head; //龟
while (h != null && h.next != null){
t = t.next;
h = h.next.next;
if ( t == h){
t = head;
while (true){
if (t == h){
return t;
}
t = t.next;
h = h.next;
}
}
}
return null;
}
//合并两个有序的数组,方法1——递归
//这里题目稍作改动:一个数组,前一部分有序,后一部分也有序,现在可以将其视为两个有序数组,然后将其合并
/**
* a1:数组
* i:第一个有序区间的起始位置
* iEnd:第一个有序区间的起始位置
* i:第二个有序区间的起始位置
* iEnd:第二个有序区间的起始位置
* a2:保存合并解决
* k:给a2使用的索引
* */
public void merge1(int[] a1,int i,int iEnd,int j,int jEnd,int[] a2,int k ){
if (i > iEnd){
System.arraycopy(a1,j,a2,k,jEnd-j+1);
return;
}
if (j > jEnd){
System.arraycopy(a1,i,a2,k,iEnd-i+1);
return;
}
if(a1[i] < a1[j]){
a2[k] = a1[i];
merge1(a1,i+1,iEnd,j,jEnd,a2,k+1);
}else {
a2[k] = a1[j];
merge1(a1,i,iEnd,j+1,jEnd,a2,k+1);
}
}
//合并两个有序的数组,方法2——双指针法
public void merge2(int[] a1,int i,int iEnd,int j,int jEnd,int[] a2){
int k = 0;
while (i <= iEnd || j <= jEnd){
if (a1[i] < a1[j]){
a2[k] = a1[i];
i++;
} else {
a2[k] = a1[j];
j++;
}
k++;
}
if (i > iEnd){
System.arraycopy(a1,j,a2,k,jEnd-j+1);
}else {
System.arraycopy(a1,i,a2,k,iEnd-i+1);
}
}
}