动态规划学习
动态规划学习
动态规划(Dynamic Programming, DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
简单来说,动态规划其实就是,给定一个问题,我们把它拆成一个个子问题,直到子问题可以直接解决。然后呢,把子问题答案保存起来,以减少重复计算。再根据子问题答案反推,得出原问题解的一种方法。一般这些子问题很相似,可以通过函数关系式递推出来。然后呢,动态规划就致力于解决每个子问题一次,减少重复计算。
动态规划核心思想
动态规划最核心的思想,就在于拆分子问题,记住过往,减少重复计算。
最简单的例子
- A : “1+1+1+1+1+1+1+1 =?”
- A : “上面等式的值是多少”
- B : 计算 “8”
- A : 在上面等式的左边写上 “1+” 呢?
- A : “此时等式的值为多少”
- B : 很快得出答案 “9”
- A : “你怎么这么快就知道答案了”
- A : “只要在8的基础上加1就行了”
- A : “所以你不用重新计算,因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”
入门
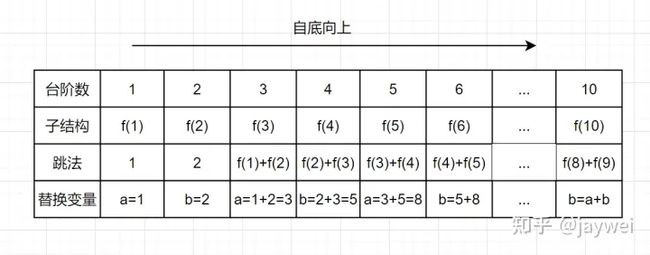
走进动态规划 – 青蛙跳阶问题
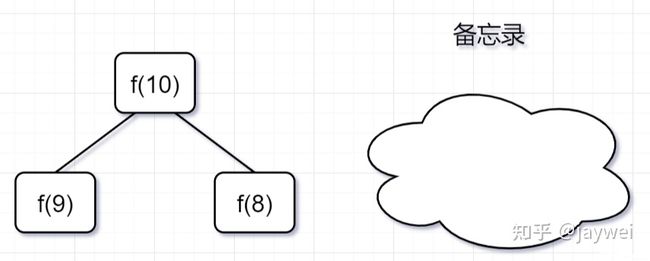
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。
试着想办法解决
- 要想跳到第10级台阶,要么是先跳到第9级,然后再跳1级台阶上去;要么是先跳到第8级,然后一次迈2级台阶上去。
- 同理,要想跳到第9级台阶,要么是先跳到第8级,然后再跳1级台阶上去;要么是先跳到第7级,然后一次迈2级台阶上去。
- 要想跳到第8级台阶,要么是先跳到第7级,然后再跳1级台阶上去;要么是先跳到第6级,然后一次迈2级台阶上去。
假设跳到第n级台阶的跳数我们定义为f(n),很显然就可以得出以下公式:
f(10) = f(9)+f(8)
f (9) = f(8) + f(7)
f (8) = f(7) + f(6)
...
f(3) = f(2) + f(1)
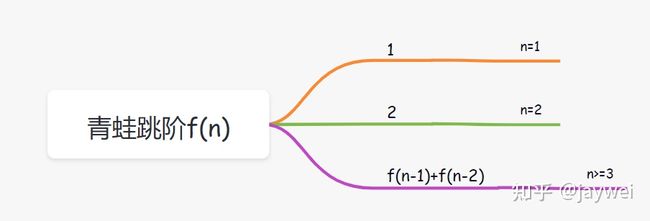
即通用公式为: f(n) = f(n-1) + f(n-2)
那f(2) 或者 f(1) 等于多少呢?
- 当只有2级台阶时,有两种跳法,第一种是直接跳两级,第二种是先跳一级,然后再跳一级。即f(2) = 2;
- 当只有1级台阶时,只有一种跳法,即f(1)= 1;
因此可以用递归去解决这个问题:
int numWays(int n) {
if(n == 1){
return 1;
}
if(n == 2){
return 2;
}
return numWays(n-1) + numWays(n-2);
}
}
这样做也可以实现但是有一个问题
程序运行需要很多时间
- 要计算原问题 f(10),就需要先计算出子问题 f(9) 和 f(8)
- 然后要计算 f(9),又要先算出子问题 f(8) 和 f(7),以此类推。
- 一直到 f(2) 和 f(1),递归树才终止。
我们先来看看这个递归的时间复杂度吧:
递归时间复杂度 = 解决一个子问题时间*子问题个数
- 一个子问题时间 = f(n-1)+f(n-2),也就是一个加法的操作,所以复杂度是 O(1);
- 问题个数 = 递归树节点的总数,递归树的总节点 = 2n-1,所以是复杂度O(2n)。
因此,青蛙跳阶,递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n),就是指数级别的,爆炸增长的,如果n比较大的话,超时很正常的了。
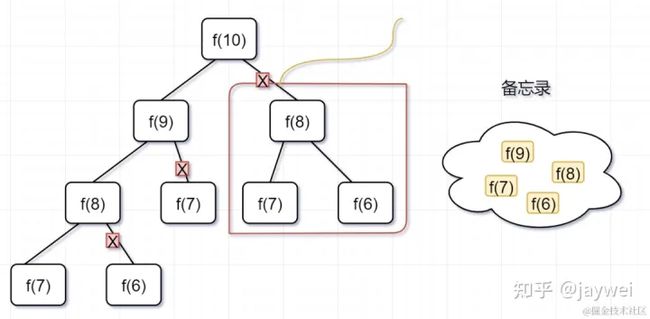
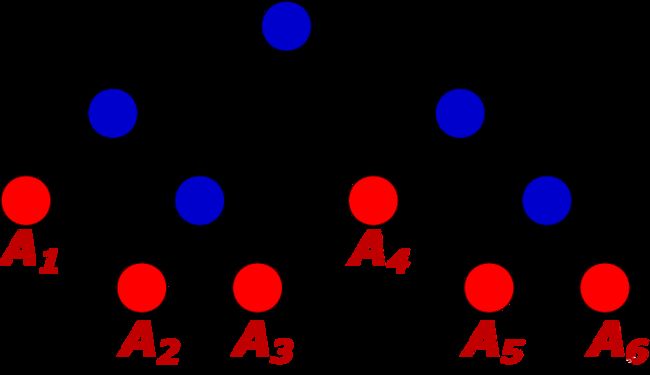
回过头来,你仔细观察这颗递归树,你会发现存在大量重复计算,比如f(8)被计算了两次,f(7)被重复计算了3次…所以这个递归算法低效的原因,就是存在大量的重复计算!
既然存在大量重复计算,那么我们可以先把计算好的答案存下来,即造一个备忘录,等到下次需要的话,先去备忘录查一下,如果有,就直接取就好了,备忘录没有才开始计算,那就可以省去重新重复计算的耗时啦!这就是带备忘录的解法。
带备忘录的递归解法(自顶向下)
一般使用一个数组或者一个哈希map充当这个备忘录。
- 第一步,f(10)= f(9) + f(8),f(9) 和f(8)都需要计算出来,然后再加到备忘录中,如下:
- 第二步, f(9) = f(8)+ f(7),f(8)= f(7)+ f(6), 因为 f(8) 已经在备忘录中啦,所以可以省掉,f(7),f(6)都需要计算出来,加到备忘录中~
第三步, f(8) = f(7)+ f(6),发现f(8),f(7),f(6)全部都在备忘录上了,所以都可以剪掉。
所以呢,用了备忘录递归算法,递归树变成光秃秃的树干咯,如下:
带备忘录的递归算法,子问题个数=树节点数=n,解决一个子问题还是O(1),所以带备忘录的递归算法的时间复杂度是O(n)。接下来呢,我们用带备忘录的递归算法去撸代码,解决这个青蛙跳阶问题的超时问题咯~,代码如下:
int numWays(int n,int *tempMap) {
// n = 0 也算1种
if (n == 0) {
return 1;
}
if (n <= 2) {
return n;
}
//先判断有没计算过,即看看备忘录有没有
if (tempMap[n]!=0) {
//备忘录有,即计算过,直接返回
return tempMap[n];
} else {
// 备忘录没有,即没有计算过,执行递归计算,并且把结果保存到备忘录map中
tempMap[n] = (numWays(n - 1,tempMap) + numWays(n - 2,tempMap)));
return tempMap[n];
}
}
这样一来程序运行的时间就大大减少了。那再来看看动态规划是怎么做的
自底向上的动态规划
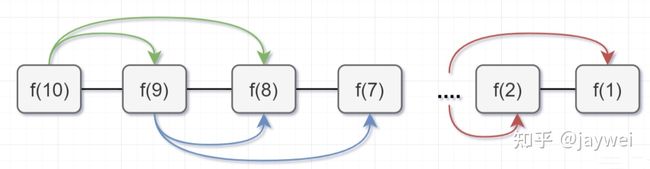
动态规划跟带备忘录的递归解法基本思想是一致的,都是减少重复计算,时间复杂度也都是差不多。但是呢:
- 带备忘录的递归,是从f(10)往f(1)方向延伸求解的,所以也称为自顶向下的解法。
- 动态规划从较小问题的解,由交叠性质,逐步决策出较大问题的解,它是从f(1)往f(10)方向,往上推求解,所以称为自底向上的解法。
动态规划有几个典型特征,最优子结构、状态转移方程、边界、重叠子问题。在青蛙跳阶问题中:
- f(n-1)和f(n-2) 称为 f(n) 的最优子结构
- f(n)= f(n-1)+f(n-2)就称为状态转移方程
- f(1) = 1, f(2) = 2 就是边界啦
- 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。
我们来看下自底向上的解法,从f(1)往f(10)方向,想想是不是直接一个for循环就可以解决啦,如下:
带备忘录的递归解法,空间复杂度是O(n),但是呢,仔细观察上图,可以发现,f(n)只依赖前面两个数,所以只需要两个变量a和b来存储,就可以满足需求了,因此空间复杂度是O(1)就可以啦
动态规划实现代码如下:
int numWays(int n) {
if (n<= 1) {
return 1;
}
if (n == 2) {
return 2;
}
int a = 1;
int b = 2;
int temp = 0;
for (int i = 3; i <= n; i++) {
temp = (a + b)% 1000000007;
a = b;
b = temp;
}
return temp;
}
动态规划的解题套路
什么样的问题可以考虑使用动态规划解决呢?
★ 如果一个问题,可以把所有可能的答案穷举出来,并且穷举出来后,发现存在重叠子问题,就可以考虑使用动态规划。
”
比如一些求最值的场景,如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等,都是动态规划的经典应用场景。
动态规划的解题思路
动态规划的核心思想就是拆分子问题,记住过往,减少重复计算。 并且动态规划一般都是自底向上的,因此到这里,基于青蛙跳阶问题,我总结了一下我做动态规划的思路:
- 穷举分析
- 确定边界
- 找出规律,确定最优子结构
- 写出状态转移方程
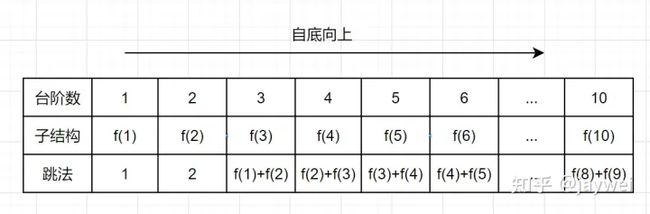
1. 穷举分析
- 当台阶数是1的时候,有一种跳法,f(1) =1
- 当只有2级台阶时,有两种跳法,第一种是直接跳两级,第二种是先跳一级,然后再跳一级。即f(2) = 2;
- 当台阶是3级时,想跳到第3级台阶,要么是先跳到第2级,然后再跳1级台阶上去,要么是先跳到第 1级,然后一次迈 2 级台阶上去。所以f(3) = f(2) + f(1) =3
- 当台阶是4级时,想跳到第3级台阶,要么是先跳到第3级,然后再跳1级台阶上去,要么是先跳到第 2级,然后一次迈 2 级台阶上去。所以f(4) = f(3) + f(2) =5
- 当台阶是5级时…
2. 确定边界
通过穷举分析,我们发现,当台阶数是1的时候或者2的时候,可以明确知道青蛙跳法。f(1) =1,f(2) = 2,当台阶n>=3时,已经呈现出规律f(3) = f(2) + f(1) =3,因此f(1) =1,f(2) = 2就是青蛙跳阶的边界。
3. 找规律,确定最优子结构
n>=3时,已经呈现出规律 f(n) = f(n-1) + f(n-2) ,因此,f(n-1)和f(n-2) 称为 f(n) 的最优子结构。什么是最优子结构?有这么一个解释:
★ 一道动态规划问题,其实就是一个递推问题。假设当前决策结果是f(n),则最优子结构就是要让 f(n-k) 最优,最优子结构性质就是能让转移到n的状态是最优的,并且与后面的决策没有关系,即让后面的决策安心地使用前面的局部最优解的一种性质
”
4, 写出状态转移方程
通过前面3步,穷举分析,确定边界,最优子结构,我们就可以得出状态转移方程啦:
5. 代码实现
我们实现代码的时候,一般注意从底往上遍历哈,然后关注下边界情况,空间复杂度,也就差不多啦。动态规划有个框架的,大家实现的时候,可以考虑适当参考一下:
dp[0][0][...] = 边界值
for(状态1 :所有状态1的值){
for(状态2 :所有状态2的值){
for(...){
//状态转移方程
dp[状态1][状态2][...] = 求最值
}
}
}
练习
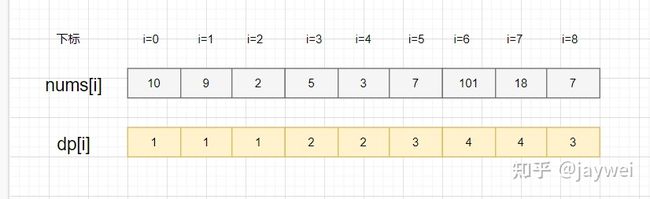
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
”
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
我们按照以上动态规划的解题思路,
- 穷举分析
- 确定边界
- 找规律,确定最优子结构
- 状态转移方程
1.穷举分析
因为动态规划,核心思想包括拆分子问题,记住过往,减少重复计算。 所以我们在思考原问题:数组num[i]的最长递增子序列长度时,可以思考下相关子问题,比如原问题是否跟子问题num[i-1]的最长递增子序列长度有关呢?
自顶向上的穷举
这里观察规律,显然是有关系的,我们还是遵循动态规划自底向上的原则,基于示例1的数据,从数组只有一个元素开始分析。
- 当nums只有一个元素10时,最长递增子序列是[10],长度是1.
- 当nums需要加入一个元素9时,最长递增子序列是[10]或者[9],长度是1。
- 当nums再加入一个元素2时,最长递增子序列是[10]或者[9]或者[2],长度是1。
- 当nums再加入一个元素5时,最长递增子序列是[2,5],长度是2。
- 当nums再加入一个元素3时,最长递增子序列是[2,5]或者[2,3],长度是2。
- 当nums再加入一个元素7时,,最长递增子序列是[2,5,7]或者[2,3,7],长度是3。
- 当nums再加入一个元素101时,最长递增子序列是[2,5,7,101]或者[2,3,7,101],长度是4。
- 当nums再加入一个元素18时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4。
- 当nums再加入一个元素7时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4.
分析找规律,拆分子问题
通过上面分析,我们可以发现一个规律:
如果新加入一个元素nums[i], 最长递增子序列要么是以nums[i]结尾的递增子序列,要么就是nums[i-1]的最长递增子序列。看到这个,是不是很开心,nums[i]的最长递增子序列已经跟子问题 nums[i-1]的最长递增子序列有关联了。
原问题数组nums[i]的最长递增子序列 = 子问题数组nums[i-1]的最长递增子序列/nums[i]结尾的最长递增子序列
是不是感觉成功了一半呢?但是如何把nums[i]结尾的递增子序列也转化为对应的子问题呢?要是nums[i]结尾的递增子序列也跟nums[i-1]的最长递增子序列有关就好了。又或者nums[i]结尾的最长递增子序列,跟前面子问题num[j](0= nums[i]的最长递增子序列,不就是从以数组num[i]每个元素结尾的最长子序列集合,取元素最多(也就是长度最长)那个嘛,所以原问题,我们转化成求出以数组nums每个元素结尾的最长子序列集合,再取最大值嘛。哈哈,想到这,我们就可以用dp[i]表示以num[i]这个数结尾的最长递增子序列的长度啦,然后再来看看其中的规律: 其实,nums[i]结尾的自增子序列,只要找到比nums[i]小的子序列,加上nums[i] 就可以啦。显然,可能形成多种新的子序列,我们选最长那个,就是dp[i]的值啦 很显然有这个规律:一个以nums[i]结尾的数组nums 当nums数组只有一个元素时,最长递增子序列的长度dp(1)=1,当nums数组有两个元素时,dp(2) =2或者1, 因此边界就是dp(1)=1。 从穷举分析,我们可以得出,以下的最优结构: max(dp(j)) 就是最优子结构。 通过前面分析,我们就可以得出状态转移方程啦: 所以数组num[i]的最长递增子序列就是: 类型一:定容求最大 题目1. 0/1背包问题 总共3件物品,背包容量50磅。物品1重10磅,价值60元,物品2重20磅,价值100元,物品3重30磅,价值120元。每个物品要装要么不装,不能只装一部分。要如何装才能让背包装到最大价值的物品。 此时我们如果用贪心算法由于物品1每磅价值6元,物品2的每磅价值5元,物品3的每磅价值4元。 很容易得到先装物品一再装物品二,但是这样的话只能背包获得180元的物品。 而装物品2和物品3,背包就能装下价值220元的物品,明显此时再用贪心算法就行不通了。这里我们需要学习并使用动态规划算法 动态规划算法的优点在于会保存之前子问题的局部最优解,并在当前计算时进行选择例如会在背包装入物品1物品2后考虑物品3时选择将物品1移出装入物品3。接下来介绍动态规划算法是如何做到的。 给定n种物品和一个背包,背包的容量为C 实例:有5个物品,其重量分别是{2, 2, 6, 5, 4},价值分别为{6, 3, 5, 4, 6},背包的容量为10。 升级 这⾥⼤家发现和⼆维dp的写法中,遍历背包的顺序是不⼀样的! 类型二:分割求最小 题目2:矩阵连乘问题 假设我们有4个矩阵,矩阵大小分别是 20 × 10 , 10 × 5 , 5 × 1 , 1 × 10 20 \times 10, 10 \times 5 ,5 \times 1,1 \times 10 20×10,10×5,5×1,1×10 如果直接按顺序乘的话需要的数乘次数为 20 × 10 × 5 + 20 × 5 × 1 + 20 × 1 × 10 = 1300 20 \times 10 \times 5 +20 \times 5 \times 1+20 \times 1 \times 10=1300 20×10×5+20×5×1+20×1×10=1300次 但是如果我们变换一下矩阵乘的次序 ( 20 × 10 ( 10 × 5 , 5 × 1 ) ) 1 × 10 (20 \times 10( 10 \times 5, 5 \times 1))1 \times 10 (20×10(10×5,5×1))1×10 需要的数乘次数为 10 × 5 × 1 + 20 × 10 × 1 + 20 × 1 × 10 = 450 10 \times 5 \times 1 +20 \times 10 \times 1+20 \times 1 \times 10=450 10×5×1+20×10×1+20×1×10=450次 可见选择不同的乘法次序消耗的资源是完全不同的,那么如何选择计算次序才能使数乘次数最少就是我们需要讨论的 给定n个矩阵:{A1, A2, ……, An},其中Ai与Ai+1可乘 ,求解这n个矩阵的连乘积: A1A2…… An P ( n ) = { 1 , n = 1 ∑ k = 1 n − 1 P ( k ) P ( n − k ) , n > 1 P(n)= \begin{cases} 1, & n=1 \\ \displaystyle\sum_{k=1}^{n-1} P(k)P(n-k), & n>1 \end{cases} P(n)=⎩ ⎨ ⎧1,k=1∑n−1P(k)P(n−k),n=1n>1 简单地递归计算m[1][n]将耗费指数时间 根据递归式自底向上计算 m[i][i]=0 [ 1 , 2 ] = [ 1 , 1 ] + [ 2 , 2 ] + 0 1 2 ( = 1 ) = 0 + 0 + 30 × 35 × 15 = 15750 [1,2]=[1,1]+[2,2]+_0 _1 _2 (=1)=0+0+30×35×15=15750 m[1,2]=m[1,1]+m[2,2]+P0P1P2(k=1)=0+0+30×35×15=15750 m [ 1 , 3 ] = m i n ( ( [ 1 , 1 ] + [ 2 , 3 ] + 0 1 3 ( = 1 ) ) , [ 1 , 2 ] + [ 3 , 3 ] + 0 2 3 ( = 2 ) ) ) = 7875 m[1,3]=min(([1,1]+[2,3] + _0 _1 _3 (=1)),[1,2]+[3,3]+_0 _2 _3 (=2)))=7875 m[1,3]=min((m[1,1]+m[2,3] + P0P1P3 (k=1)),m[1,2]+m[3,3]+P0P2P3(k=2)))=7875 构造最优解对应的问题解值 在填充表 m 的过程中设置另一张表 S 记录各个子矩阵链取最优值时的分割位置k 可知在A[1,6]中在A3处分割 升级 凸多边形最优三角剖分问题 多边形 平面上由一系列首尾相接的直线段组成的分段线性闭曲线 简单多边形 若多边形的边除了连接顶点外没有别的交点,称为简单多边形 凸多边形 当一个简单多边形及其内部构成一个闭凸集时,称为凸多边形 凸集的含义:凸多边形边界或内部的任意两点所连成的直线段上的所有点均在凸多边形的内部或边界上 通常用多边形顶点的逆时针序列表示凸多边形 即: V={v0, v1, ……, vn-1} 表示具有n条边**(v0, v1),(v1, v2 ),……,(vn-1 , vn)**的一个凸多边形(约定:v0 =vn ) 凸多边形的分割 若 vi 和 vj 是多边形中两个不相邻的顶点 •则线段(vi, vj)称为多边形的一条弦 一条弦将多边形分割成两个多边形: •{ vi, vi+1, ……, vj } 和 { vj, vj+1, ……, vi } 例1:{ v0, v1, v2, v3 } 和 { v3, v4, v5, v6, v0 } 例2:{ v1, v2, v3, v4 } 和 { v4, v5, v6, v0 , v1 } 凸多边形的三角剖分 凸多边形的三角剖分是 •将多边形P分割成互不相交的三角形的弦的集合T •在该剖分中各弦互不相交,且集合T已达到最大 ±在有n个顶点的凸多边形的三角剖分中 凸多边形的最优三角剖分问题 ±给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数W,要求确定该凸多边形的三角剖分,使得该三角剖分中诸三角形上权值之和为最小 ±三角形的权函数W可以有多种定义方式 •例如:W(vivjvk)=|vivj|+|vjvk|+|vkvi| •其中: |vivj| 表示顶点 vi 到 vj 的欧式距离 •对应于该权函数的最优三角剖分称为最小弦长三角剖分 矩阵连乘的最优计算次序等价于矩阵链的最优完全加括号方式 一个表达式的完全加括号方式相当于一棵平衡二叉树 例如:完全加括号的矩阵连乘积((A1(A2A3))(A4(A5A6))) 可以用如下的平衡二叉树进行表示 其中:叶节点为表达式中的原子;树根表示左右子树相结合 这样的二叉树称为该表达式的语法树 凸多边形三角剖分也可以用语法树来表示(如图) 该语法树的根节点为边(v0, v6 ) 三角剖分中的弦组成其余的内节点(子树的根节点) 多边形中除(v0, v6 )外的各条边都是语法树的一个叶节点 例如:以弦(v0, v3 )和(v3, v6 )为根的子树表示? 凸多边形**{ v0, v1, v2, v3** } 和 **{ v3, v4, v5, v6}**的三角剖分 凸多边形三角剖分与矩阵连乘问题的同构关系 凸n边形的三角剖分和有n-1个叶节点的语法树存在一一对应关系。 n个矩阵的完全加括号乘积和有n个叶节点的语法树存在一一对应关系。 推论:n个矩阵连乘的完全加括号和凸n+1边形的三角剖分也存在一一对应关系。其中,矩阵Ai对应于凸多边形中的一条边(vi-1, vi) ,三角剖分中的每条弦(vi , vj )对应于一组矩阵的连乘积A[i+1, j] 矩阵连乘的最优计算次序问题是凸多边形最优三角剖分的特例 对于给定的矩阵链: (A1 A2 … An) 定义一个与之相应的凸多边形:P={v0, v1, ……, vn} 使得矩阵 Ai 与凸多边形的边(vi-1, vi)一一对应 若矩阵 Ai 的维数为:pi-1 x pi 定义三角形(vivjvk)上的权函数值:w(vivjvk)=pi x pj x pk 则:凸多边形P的最优三角剖分所对应的语法树 同时 也给出了该矩阵链A1A2 … An 的最优完全加括号方式 凸多边形最优三角剖分的递归结构 设:t[i][j](1 ≤ i ≤ j ≤ n)为凸子多边形p{vi-1,vi,…vj}的最优三角剖分所对应的权函数值,即三角剖分的最优值 设:退化的两顶点多边形{vi-1vi}的具有权值0(t[i][i]=0) 则:原问题(凸(n+1)边形)的最优权值为:t[1][n] 当(j-i)≥1时:凸子多边形{vi-1,vi,…vj}至少有三个顶点 设k为其中一个中间点(i≤ k < j),由最优子结构性质 t[i] [j]的值应为三部分权值之和:两个凸子多边形的最优权值t[i] [k]和t[k+1] [j],加上三角形$vi-1vkvj的权值 由于k的可能位置有j-i个,因此问题转化为:在其中选择使得t[i][j]达到最小的位置。相应地得到t[i][j]的递归定义如下: t [ i ] [ j ] = { 0 i = j min i < = k < j { t [ i ] [ k ] + t [ k + 1 ] [ j ] + w ( v i − 1 v k v j ) } i < j t[i][j]=\left\{\begin{array}{cc}0 & i=j \\ \min _{i<=k 计算凸多边形最优三角剖分的最优值 ™与矩阵连乘问题相比,除了权函数的定义外,**t[i][j]与m[i][j]**的递归式完全相同,因此只需对MatrixChain算法做少量修改即可 m [ i , j ] = { 0 i = j min i ≤ k < j { m [ i ] [ k ] + m [ k + 1 ] [ j ] + p i − 1 p k p j } i < j m[i, j]=\left\{\begin{array}{cc}0 & i=j \\ \min _{i \leq \mathrm{k}<\mathrm{j}}\left\{m[i][k]+m[k+1][j]+p_{i-1} p_k p_j\right\} & i t [ i ] [ j ] = { 0 i = j min i ≤ k < j { t [ i ] [ k ] + t [ k + 1 ] [ j ] + w ( v i − 1 v k v j ) } i < j t[i][j]=\left\{\begin{array}{cc}0 & i=j \\ \min _{i \leq k 复杂度分析: 与矩阵连乘算法的复杂度是一样的 算法有三重循环,元运算的总次数为O(n3) 因此算法的计算时间上界为O(n3) 算法所占用的空间为O(n2) 构造凸多边形最优三角剖分(最优解) 凸多边形最优三角剖分的最优解 计算最优值t[1] [n]时,可以用数组S记录三角剖分信息 S[i][j]记录与**(vi-1,** **vj)**共同组成三角形的第三个顶点的位置 据此在O(n)时间内可以构造出最优三角剖分当中的所有三角形 关于动态规划,还有 树形DP,数位DP,区间DP ,概率型DP,博弈型DP,状态压缩DP等等等,有兴趣的话可以自行学习。 总结 动态规划算法与贪心算法类似,其基本思想也是将待求解问题分解成若干个子问题,但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法。 1.找出最优解的性质(分析其结构特征) 各分解得到的子问题往往不是互相独立的;
5结尾的最长子序列就是[2,5],因为从数组下标0到3遍历,只找到了子序列[2]比5小,所以就是[2]+[5]啦,即dp[4]=23结尾的最长子序列就是[2,3],因为从数组下标0到4遍历,只找到了子序列[2]比3小,所以就是[2]+[3]啦,即dp[4]=27结尾的最长子序列就是[2,5,7]和[2,3,7],因为从数组下标0到5遍历,找到2,5和3都比7小,所以就有[2,7],[5,7],[3,7],[2,5,7]和[2,3,7]这些子序列,最长子序列就是[2,5,7]和[2,3,7],它俩不就是以5结尾和3结尾的最长递增子序列+[7]来的嘛!所以,**dp[5]=3 =dp[3]+1=dp[4]+1**。
最简单的边界情况
确定最优子结构
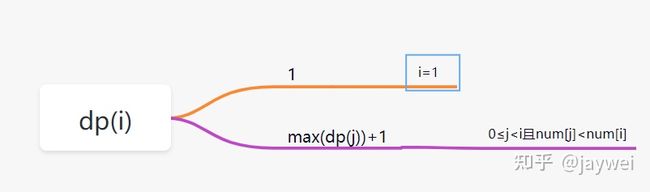
dp(i) =max(dp(j))+1,存在j属于区间[0,i-1],并且num[i]>num[j]。
状态转移方程
最长递增子序列 =max(dp[i])
代码实现
public int lengthOfLIS(int[] nums) {
if (nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
//初始化就是边界情况
dp[0] = 1;
int maxans = 1;
//自底向上遍历
for (int i = 1; i < nums.length; i++) {
dp[i] = 1;
//从下标0到i遍历
for (int j = 0; j < i; j++) {
//找到前面比nums[i]小的数nums[j],即有dp[i]= dp[j]+1
if (nums[j] < nums[i]) {
//因为会有多个小于nums[i]的数,也就是会存在多种组合了嘛,我们就取最大放到dp[i]
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
//求出dp[i]后,dp最大那个就是nums的最长递增子序列啦
maxans = Math.max(maxans, dp[i]);
}
return maxans;
}
进阶
设物品i的重量是W[i],其价值为V[i] 。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
限制条件:在选择装入背包的物品时,对每种物品i只有2种选择,即装入背包或不装入背包;不能将物品 i 装入背包多次,也不能只装入部分的物品 i 。
(1)0-1背包问题的形式化描述
优化目标函数:max( ∑ i = 1 n v i x i \displaystyle\sum_{i=1}^{n} v_ix_i i=1∑nvixi)
其中: x = (x1,x2,…,xn) 为 n 元 0-1 向量
约束条件: ∑ i = 1 n w i x i ≤ c \displaystyle\sum_{i=1}^{n} w_ix_i \leq c i=1∑nwixi≤c ( x i x_i xi∈{0,1})
(2)证明0/1背包问题是最优子结构
最优子结构:原问题的最优解包含其子问题的最优解。对背包问题而言:
如果(x1, x2, …, xn)是所给0/1背包问题的一个最优解,
∑ i = 1 n w i x i ≤ c \displaystyle\sum_{i=1}^{n} w_ix_i \leq c i=1∑nwixi≤c ( x i x_i xi∈{0,1} 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n)
max( ∑ i = 1 n v i x i \displaystyle\sum_{i=1}^{n} v_ix_i i=1∑nvixi)
若能证明(x2, …, xn)是下面子问题的最优解:
∑ i = 2 n w i x i ≤ c − w 1 x 1 \displaystyle\sum_{i=2}^{n} w_ix_i \leq c-w_1x_1 i=2∑nwixi≤c−w1x1 ( x i x_i xi∈{0,1} 2 ≤ i ≤ n 2 \leq i \leq n 2≤i≤n)
max( ∑ i = 2 n v i x i \displaystyle\sum_{i=2}^{n} v_ix_i i=2∑nvixi)
则0/1背包问题具有最优子结构性质。
设(x1, x2, …, xn)是所给0/1背包问题的一个最优解,则( x2, …, xn)是下面一个子问题的最优解:
∑ i = 2 n w i x i ≤ c − w 1 x 1 \displaystyle\sum_{i=2}^{n} w_ix_i \leq c-w_1x_1 i=2∑nwixi≤c−w1x1 ( x i x_i xi∈{0,1} 2 ≤ i ≤ n 2 \leq i \leq n 2≤i≤n)
max( ∑ i = 2 n v i x i \displaystyle\sum_{i=2}^{n} v_ix_i i=2∑nvixi)
如若不然,设(y2, …, yn)是上述子问题的一个最优解,则
∑ i = 2 n v i y i \displaystyle\sum_{i=2}^{n} v_iy_i i=2∑nviyi> ∑ i = 2 n v i x i \displaystyle\sum_{i=2}^{n} v_ix_i i=2∑nvixi
w 1 x 1 + ∑ i = 2 n v i y i ≤ c w_1x_1+\displaystyle\sum_{i=2}^{n} v_iy_i \leq c w1x1+i=2∑nviyi≤c
因此,
v 1 x 1 + ∑ i = 2 n v i y i v_1x_1+\displaystyle\sum_{i=2}^{n} v_iy_i v1x1+i=2∑nviyi> v 1 x 1 + ∑ i = 2 n v i x i v_1x_1+\displaystyle\sum_{i=2}^{n} v_ix_i v1x1+i=2∑nvixi= ∑ i = 1 n v i x i \displaystyle\sum_{i=1}^{n} v_ix_i i=1∑nvixi
这说明(x1, y2, …, yn)是所给0/1背包问题比(x1, x2, …, xn)更优的解,从而导致矛盾。
反证得0/1背包问题具有最优子结构
(3)用动态规划思想解决问题
0/1背包问题可以看作是决策一个序列(x1, x2, …, xn),对任一变量xi的决策是决定xi=1还是xi=0。在对xi-1决策后,已确定了(x1, …, xi-1),在决策xi时,问题处于下列两种状态之一:
(1)背包容量不足以装入物品i,则xi=0,背包不增加价值;
(2)背包容量可以装入物品i。
在(2)的状态下,物品i有两种情况,装入(则xi=1)或不装入(则xi=0)。在这两种情况下背包价值的最大者应该是对xi决策后的背包价值。
令V(i, j)表示在前i(1≤i≤n)个物品中能够装入容量为j(1≤j≤C)的背包中的物品的最大价值,则可以得到如下动态规划函数:V(i,0)=V(0,j)=0
V ( i , j ) = { V ( i − 1 , j ) , j < w i m a x ( V ( i − 1 , j ) , V ( i − 1 , j − w i ) + v i ) , j ≥ w i V(i,j)= \begin{cases} V(i-1,j), & j
式1表明:把前面i个物品装入容量为0的背包和把0个物品装入容量为j的背包,得到的价值均为0。
式2的第一个式子表明:如果第i个物品的重量大于背包的容量,则物品i不能装入背包,则装入前i个物品得到的最大价值和装入前i-1个物品得到的最大价值是相同的。
式2的第二个式子表明:如果第i个物品的重量小于背包的容量,则会有以下两种情况:
如果第i个物品没有装入背包,则背包中物品的价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。
如果把第i个物品装入背包,则背包中物品的价值等于把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi;
显然,取二者中价值较大者作为把前i个物品装入容量为j的背包中的最优解。
根据动态规划函数,用一个(n+1)×(C+1)的二维表V,V[i][j]表示把前i个物品装入容量为j的背包中获得的最大价值。
V ( i , j ) = { V ( i − 1 , j ) , j < w i m a x ( V ( i − 1 , j ) , V ( i − 1 , j − w i ) + v i ) , j ≥ w i V(i,j)= \begin{cases} V(i-1,j), & j
按下述方法来划分阶段:第一阶段,只装入前1个物品,确定在各种情况下的背包能够得到的最大价值;第二阶段,只装入前2个物品,确定在各种情况下的背包能够得到的最大价值;依此类推,直到第n个阶段。最后,V(n,C)便是在容量为C的背包中装入n个物品时取得的最大价值。
为了确定装入背包的具体物品,从V(n,C)的值向前推,如果V(n,C)>V(n-1,C),表明第n个物品被装入背包,前n-1个物品被装入容量为C-wn的背包中;否则,第n个物品没有被装入背包,前n-1个物品被装入容量为C的背包中。依此类推,直到确定第1个物品是否被装入背包中为止。由此,得到如下函数:
x i = { 0 , V ( i , j ) = V ( i − 1 , j ) 1 , j = j − w i ; V ( i , j ) > V ( i − 1 , j ) x_i= \begin{cases} 0, & V(i,j)=V(i-1,j) \\ 1, & j =j-w_i ;V(i,j)>V(i-1,j)\end{cases} xi={0,1,V(i,j)=V(i−1,j)j=j−wi;V(i,j)>V(i−1,j)int KnapSack(int n, int w[ ], int v[ ]) {
for (i=0; i<=n; i++) //初始化第0列
V[i][0]=0;
for (j=0; j<=C; j++) //初始化第0行
V[0][j]=0;
for (i=1; i<=n; i++) //计算第i行,进行第i次迭代
for (j=1; j<=C; j++)
if (j<w[i]) V[i][j]=V[i-1][j];
else V[i][j]=max(V[i-1][j], V[i-1][j-w[i]]+v[i]);
j=C; //求装入背包的物品
for (i=n; i>0; i--){
if (V[i][j]>V[i-1][j]) {
x[i]=1;
j=j-w[i];
}
else x[i]=0;
}
return V[n][C]; //返回背包取得的最大价值
}
此时我们构造了一个二维数组来存放子问题结果方便以后查询,这样一来虽然时间复杂度降低了,但是空间复杂度提升了,接下来介绍如何降低空间复杂度
对于背包问题其实状态都是可以压缩的。
在使⽤⼆维数组的时候,递推公式:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] +value[i]);
其实可以发现如果把dp[i - 1]那⼀层拷贝到dp[i]上,表达式完全可以是:
dp[i][j] =max(dp[i][j], dp[i][j - weight[i]] + value[i]);
于其把dp[i - 1]这⼀层拷贝到dp[i]上,不如只⽤⼀个⼀维数组了,只⽤dp[j](⼀维数组,也可以理解是⼀个滚动数组)。
这就是滚动数组的由来,需要满⾜的条件是上⼀层可以重复利⽤,直接拷贝到当前层。
读到这⾥估计⼤家都忘了 dp[i][j]⾥的i和j表达的是什么了,i是物品,j是背包容量。
dp[i][j] 表⽰从下标为[0-i]的物品⾥任意取,放进容量为j的背包,价值总和最⼤是多少。
⼀定要时刻记住这⾥i和j的含义,要不然很容易看懵了。
动规五部曲分析如下:
在⼀维dp数组中,dp[j]表⽰:容量为j的背包,所背的物品价值可以最⼤为dp[j]。
dp[j]为 容量为j的背包所背的最⼤价值,那么如何推导dp[j]呢?
dp[j]可以通过dp[j - weight[j]]推导出来,dp[j - weight[i]]表⽰容量为j - weight[i]的背包所背
的最⼤价值。
dp[j - weight[i]] + value[i] 表⽰ 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容
量为j的背包,放⼊物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,⼀个是取⾃⼰dp[j],⼀个是取dp[j - weight[i]] + value[i],指定是取
最⼤的,毕竟是求最⼤价值,
所以递归公式为:
可以看出相对于⼆维dp数组的写法,就是把dp[i][j]中i的维度去掉了。
关于初始化,⼀定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
dp[j]表⽰:容量为j的背包,所背的物品价值可以最⼤为dp[j],那么dp[0]就应该是0,因为
背包容量为0所背的物品的最⼤价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
看⼀下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候⼀定是取价值最⼤的数,如果题⽬给的价值都是正整数那么⾮0下标都
初始化为0就可以了,如果题⽬给的价值有负数,那么⾮0下标就要初始化为负⽆穷。
这样才能让dp数组在递归公式的过程中取的最⼤的价值,⽽不是被初始值覆盖了。
那么我假设物品价值都是⼤于0的,所以dp数组初始化的时候,都初始为0就可以了。
⼀维dp数组遍历顺序
代码如下:for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
⼆维dp遍历的时候,背包容量是从⼩到⼤,⽽⼀维dp遍历的时候,背包是从⼤到⼩。
为什么呢?
倒叙遍历是为了保证物品i只被放⼊⼀次!,在动态规划:关于01背包问题,你该了解这
些!中讲解⼆维dp数组初始化dp[0][j]时候已经讲解到过⼀次。
举⼀个例⼦:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放⼊了两次,所以不能正序遍历。
为什么倒叙遍历,就可以保证物品只放⼊⼀次呢?
倒叙就是先算dp[2]
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取⼀次了。
那么问题又来了,为什么⼆维dp数组历的时候不⽤倒叙呢?
因为对于⼆维dp,dp[i][j]都是通过上⼀层即dp[i - 1][j]计算⽽来,本层的dp[i][j]并不会被覆
盖!
(如何这⾥读不懂,⼤家就要动⼿试⼀试了,空想还是不靠谱的,实践出真知!)
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先
遍历背包容量嵌套遍历物品呢?
不可以!
因为⼀维dp的写法,背包容量⼀定是要倒序遍历(原因上⾯已经讲了),如果遍历背包容
量放在上⼀层,那么每个dp[j]就只会放⼊⼀个物品,即:背包⾥只放⼊了⼀个物品。
(这⾥如果读不懂,就在回想⼀下dp[j]的定义,或者就把两个for循环顺序颠倒⼀下试
试!)
所以⼀维dp数组的背包在遍历顺序上和⼆维其实是有很⼤差异的!,这⼀点⼤家⼀定要注
意。
⼀维dp01背包完整C++测试代码:void test_1_wei_bag_problem() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagWeight = 4;
// 初始化
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
问题:如何确定计算矩阵连乘积的计算次序
使得依此次序计算矩阵连乘积需要的数乘次数最少
思考
首先想到可以使用穷举法,列举出所有可能的计算次序,从中找出数乘次数最少的次序
由于每种加括号方式都可以分解为两个子矩阵的加括号问题:(A1…Ak)(Ak+1…An),可得n个矩阵连乘积可能的计算次序总数P(n)递推式为
算出 P ( n ) = Ω ( 4 n / n 3 / 2 ) P(n)=\Omega(4^n/n^{3/2}) P(n)=Ω(4n/n3/2)
可知用穷举法n个矩阵连乘积可能的计算次序总数P(n)随n的增长呈指数增长,因此穷举法不是一个有效的算法
找出最优解性质
由选择矩阵进行相乘得到一个数乘次数如同0/1背包问题中选择物品得到一个总价值且都是通过最优选择得到最优解,尝试是否能用动态规划算法
首先应分析问题的最优解结构特征
将矩阵连乘积 (Ai Ai+1 … Aj) 简记为A[i:j]
考察计算A[1:n]的最优计算次序:
设最优计算次序在Ak和Ak+1之间将矩阵链断开(1≤k
总计算量为如下三部分计算量之和:
求解A[1:k]的计算量
求解A[k+1:n]的计算量
求解A[1:k]和A[k+1:n]相乘的计算量
由于A[1:n]是一个最优计算次序那么A[1:k]和A[k+1:n]的计算次序也是最优
说明矩阵连乘计算次序问题的最优解包含着其子问题的最优解,我们可以使用动态规划算法求解。
建立递归关系
设:计算A[i:j]所需要的最少数乘次数为m[i][j](1≤i≤j≤n)
则:原问题的最优值为m[1][n]
当 i=j 时,A[i:j]=Ai,因此:m[i][i]=0
当 i
则:m[i][j]=m[i][k]+m[k+1][j]+ Pi-1 Pk Pj
k的取值只有j-i个可能,即:k∈{i, i+1, …, j-1}
k是其中使计算量达到最小的位置,因此m[i][j]可定义为
m [ i , j ] = { 0 , i = j min i ≤ k < j n − 1 ( m [ i , k ] + m [ k + 1 , j ] + p i − 1 p k p j ) , i < j m[i,j]= \begin{cases} 0, & i=j \\ \displaystyle\min_{i \leq k
计算最优值
依据其递归式以自底向上的方式进行计算
在计算过程中,保存已解决的子问题答案
每个子问题只计算一次,而在后面需要时只要简单查一下,从而避免大量的重复计算,最终得到多项式时间的算法
在递归计算时,许多子问题被重复计算多次
考虑 1≤i≤j≤n 的所有可能情况
不同的有序对 (i, j) 对应于不同的子问题
因此,不同子问题的个数最多只有:
( n 2 ) \begin{pmatrix} n\\ 2\end{pmatrix} (n2)= n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)= n 2 − n 2 \frac{n^2-n}{2} 2n2−n
实例
A1
A2
A3
A4
A5
A6
30*35
35*15
15*5
5*10
10*20
20*25
m
A1
A2
A3
A4
A5
A6
A1
0
A2
0
A3
0
A4
0
A5
0
A6
0
s
1
2
3
4
5
6
1
0
2
0
3
0
4
0
5
0
6
0
m
A1
A2
A3
A4
A5
A6
A1
0
15750
A2
0
2625
A3
0
750
A4
0
1000
A5
0
5000
A6
0
s
1
2
3
4
5
6
1
0
1
2
0
2
3
0
3
4
0
4
5
0
5
6
0
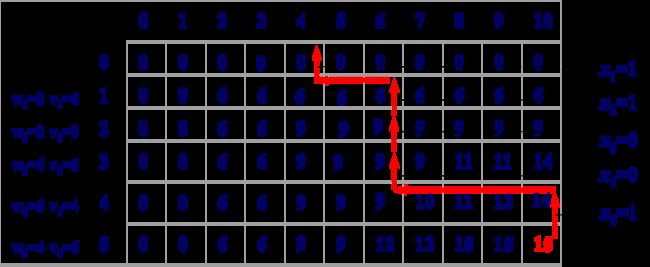
[ 2 , 3 ] = [ 2 , 2 ] + [ 3 , 3 ] + 1 2 3 ( = 2 ) = 0 + 0 + 30 × 15 × 5 = 2625 [2,3]=[2,2] + [3,3]+_1 _2 _3 (=2)=0+0+30×15×5=2625 m[2,3]=m[2,2] + m[3,3]+P1P2P3(k=2)=0+0+30×15×5=2625
[ 3 , 4 ] = [ 3 , 3 ] + [ 4 , 4 ] + 2 3 4 ( = 3 ) = 0 + 0 + 15 × 5 × 10 = 750 [3,4]=[3,3]+[4,4]+_2 _3 _4 (=3)=0+0+15×5×10=750 m[3,4]=m[3,3]+m[4,4]+P2P3P4(k=3)=0+0+15×5×10=750
[ 4 , 5 ] = [ 4 , 4 ] + [ 5 , 5 ] + 3 4 5 ( = 4 ) = 0 + 0 + 5 × 10 × 20 = 1000 [4,5]=[4,4]+[5,5]+_3 _4 _5 (=4)=0+0+5×10×20=1000 m[4,5]=m[4,4]+m[5,5]+P3P4P5(k=4)=0+0+5×10×20=1000
[ 5 , 6 ] = [ 5 , 5 ] + [ 6 , 6 ] + 4 5 6 ( = 5 ) = 0 + 0 + 10 × 20 × 25 = 5000 [5,6]=[5,5]+[6,6]+_4 _5 _6 (=5)=0+0+10×20×25=5000 m[5,6]=m[5,5]+m[6,6]+P4P5P6(k=5)=0+0+10×20×25=5000
m
A1
A2
A3
A4
A5
A6
A1
0
15750
7875
A2
0
2625
4375
A3
0
750
2500
A4
0
1000
3500
A5
0
5000
A6
0
s
1
2
3
4
5
6
1
0
1
1
2
0
2
3
3
0
3
3
4
0
4
5
5
0
5
6
0
m [ 2 , 4 ] = m i n ( ( [ 2 , 2 ] + [ 3 , 4 ] + 1 2 4 ( = 2 ) ) , [ 2 , 3 ] + [ 4 , 4 ] + 1 3 4 ( = 3 ) ) ) = 4375 m[2,4]=min(([2,2]+[3,4]+_1 _2 _4 (=2)),[2,3]+[4,4]+_1 _3 _4 (=3)))=4375 m[2,4]=min((m[2,2]+m[3,4]+P1P2P4(k=2)),m[2,3]+m[4,4]+P1P3P4(k=3)))=4375
m [ 3 , 5 ] = m i n ( ( [ 3 , 3 ] + [ 4 , 5 ] + 2 3 5 ( = 3 ) ) , [ 3 , 4 ] + [ 5 , 5 ] + 2 4 5 ( = 4 ) ) ) = 2500 m[3,5]=min(([3,3]+[4,5]+_2 _3 _5 (=3)),[3,4]+[5,5]+_2 _4 _5 (=4)))=2500 m[3,5]=min((m[3,3]+m[4,5]+P2P3P5(k=3)),m[3,4]+m[5,5]+P2P4P5(k=4)))=2500
m [ 4 , 6 ] = m i n ( ( [ 4 , 4 ] + [ 5 , 6 ] + 3 4 6 ( = 4 ) ) , [ 4 , 5 ] + [ 6 , 6 ] + 3 5 6 ( = 5 ) ) ) = 3500 m[4,6]=min(([4,4]+[5,6]+_3 _4 _6 (=4)),[4,5]+[6,6]+_3 _5 _6 (=5)))=3500 m[4,6]=min((m[4,4]+m[5,6]+P3P4P6(k=4)),m[4,5]+m[6,6]+P3P5P6 (k=5)))=3500
m
A1
A2
A3
A4
A5
A6
A1
0
15750
7875
9375
A2
0
2625
4375
7125
A3
0
750
2500
5375
A4
0
1000
3500
A5
0
5000
A6
0
s
1
2
3
4
5
6
1
0
1
1
3
2
0
2
3
3
3
0
3
3
3
4
0
4
5
5
0
5
6
0
m
A1
A2
A3
A4
A5
A6
A1
0
15750
7875
9375
11875
A2
0
2625
4375
7125
10500
A3
0
750
2500
5375
A4
0
1000
3500
A5
0
5000
A6
0
s
1
2
3
4
5
6
1
0
1
1
3
3
2
0
2
3
3
3
3
0
3
3
3
4
0
4
5
5
0
5
6
0
m
A1
A2
A3
A4
A5
A6
A1
0
15750
7875
9375
11875
15125
A2
0
2625
4375
7125
10500
A3
0
750
2500
5375
A4
0
1000
3500
A5
0
5000
A6
0
s
1
2
3
4
5
6
1
0
1
1
3
3
3
2
0
2
3
3
3
3
0
3
3
3
4
0
4
5
5
0
5
6
0
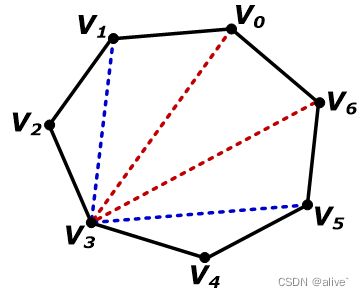
S[i][j]=k表示:A[i:j] 的最优划分方式是 (A[i:k])(A[k+1:j])
可以据此构造矩阵链的最优计算次序
从s[1,n]记录的信息可以知道A[1:n]的最佳划分方式
即:(A[1 : k])(A[k+1 : n]) 其中:k = S[1, n]
其中:A[1 : k]和A[k+1:n]的最佳划分方式可以递归地得到
即:(A[1 : x])(A[x+1: k]) 其中:x = S[1, k]
和:(A[k+1 : y])(A[y+1: n]) 其中:y = S[k+1, n]
由此递归下去,可以得到最优完全加括号方式,即构造出一个最优解
m
A1
A2
A3
A4
A5
A6
A1
0
15750
7875
9375
11875
15125
A2
0
2625
4375
7125
10500
A3
0
750
2500
5375
A4
0
1000
3500
A5
0
5000
A6
0
s
1
2
3
4
5
6
1
0
1
1
3
3
3
2
0
2
3
3
3
3
0
3
3
3
4
0
4
5
5
0
5
6
0
(A1A2A3)(A4A5A6)
而在A[1,3]中在A1处分割,在A[4,6]中在A5处分割
可得最终结果最优解为: (A1(A2A3))((A4A5)A6)
代码void MatrixChain(int *p,int n,int **m,int **s)
{
for (int i = 1; i <= n; i++) m[i][i] = 0;
for (int r = 2; r <= n; r++) //r表示链长,取值2~n
for (int i = 1; i <= n - r+1; i++) {
int j=i+r-1; //j依次取值i+1,i+2,……,n
m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];
//即m[i][j] = m[i][i]+m[i+1][j]+ p[i-1]*p[i]*p[j]
s[i][j] = i; //i为初始断开位置
for (int k = i+1; k < j; k++) {//依次设断开位置为i+1,i+2,……
int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}
}
}
}
template<class type>
void minweighttriangulation(int n, type ** t, int **s)
{ for (int i=1; i<=n; i++) t[i][i]=0;
for (int r=2; r<=n; r++)
for (int i=1; i<=n-r+1; i++)
{ int j=i+r-1;
t[i][j]= t[i+1][j]+w(i-1,i,j);
s[i][j]=i;
for (int k=i+1; k<=i+r+1; k++)
{ int u= t[i][k]+t[k+1][j]+w(i-1,k,j) ;
if (u< t[i][j])
{t[i][j]= u; s[i][j]=k; }
}
}
}
S
1
2
3
4
5
6
1
0
1
1
3
3
3
2
0
2
3
3
3
3
0
3
3
3
4
0
4
5
5
0
5
6
0
拓展
1.算法定义
动态规划法的基本思路是:构造一张表来记录所有已解决的子问题的答案2.算法步骤
2.递归地定义最优值(优化目标函数)
3.以自底向上的方式计算出最优值
4.根据计算最优值时得到的信息,构造最优解3.算法应用
基本要素
1.最优子结构
2.重叠子问题