二叉树练习(二):树的双亲表示法及其部分算法实现
注意,本文归类于“二叉树练习”系列文章,但具体的解释、实现均为普通的树而并非二叉树,望读者注意。
概念
双亲表示法,即储存树结点的同时储存其所属的父结点的表示法,通常利用顺序表(数组)实现。使用双亲表示法储存树,使得树具有如下特性:
- 可以快速地找到一个结点的父结点
- 寻找一个结点的子节点需要遍历整颗树
结构定义
使用C++实现。需要注意,Tree结构体内的Node数组不是以指针的形式定义,而下文Tree结构体却使用指针来储存,要注意区分指针的解引用符号“->”和对象的“.”符号的区别。
const int MAX_SIZE = 102; //数组的大小,即整颗树可以有的最多结点数量,我定为102
//树结点
struct Node
{
char data; //树结点所携带的数据
int parent; //该结点对应的父亲结点的数组下标
};
//树
struct Tree
{
Node nodes[MAX_SIZE]; //存放所有树结点的数组
int size; //树结点数量
};创建树
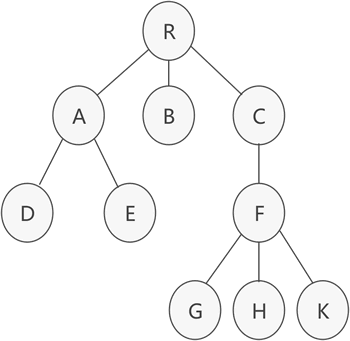
为方便起见,这里使用王道数据结构书里给的树结构作为例子,树的结构示意图如下:
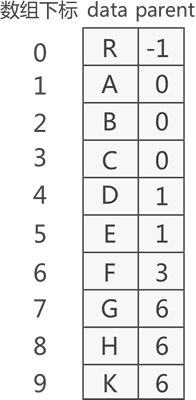
使用双亲表示法表示后:
代码:
Tree *CreateTree()
{
Tree *tree = (Tree *)malloc(sizeof(Tree)); //分配动态内存
memset(tree->nodes, 0, sizeof(tree->nodes)); //别忘了把数组内容清空
const char def_data[] = {'R', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'K'}; //结点数据
const int def_parent[] = {-1, 0, 0, 0, 1, 1, 3, 6, 6, 6}; //结点对应的父结点的下标
const int sz = 10; //树的结点树
//使用循环将内容复制进树结点数组即可
for (int i = 0; i < sz; ++i)
{
Node &node = tree->nodes[i];
node.data = def_data[i];
node.parent = def_parent[i];
}
tree->size = sz;
return tree;
}计算树的高度
由于双亲表示法只保存了结点到其父节点的指针(即是下标),树的高度即为最高的结点高度,要计算结点的高度,即需要沿着它的父结点一直往上走直到根结点为止,这样就能计算出一个结点的高度,然后对树中所有结点都计算一遍高度,最高的高度即为树的高度,这是非常粗暴的方法。
代码实现:
int GetHeight(Tree *tree)
{
int maxh = 0; //当前最高的结点的高度,如果树没有节点,高度为0
// 遍历所有树结点
for (int i = 0; i < tree->size; ++i)
{
Node *node = &tree->nodes[i];
int h = 1; //结点的初始高度
// 沿着每个结点的父结点往上走直到根节点为止
while (node->parent != -1)
{
node = &tree->nodes[node->parent];
++h;
}
maxh = max(maxh, h); //若该结点的高度高于当前最高结点,则更新最高高度
}
return maxh; //最高的结点的高度即为树的高度
}这里其实还有一种优化的思路,即对于每个计算过高度的结点都利用哈希表缓存起来,下次只要遇到父结点是计算过高度的结点就可以直接加上它父结点的高度,而不需要重复计算高度。
输出所有叶子结点
因为无法从结构中得知哪个节点是叶子结点,所以对于某一个结点,只能遍历其他所有结点检查是否有结点以它为父结点,若无,则该结点是叶结点,同理,该思路也可用于计算叶结点的数量。
代码:
void PrintAllLeaves(Tree *tree)
{
int sz = tree->size;
if (sz == 0) // 空树,直接返回
return;
cout << "Leaves: ";
//遍历所有结点
for (int i = 0; i < sz; ++i)
{
bool isleaf = true; //用以标记当前结点是否是叶结点
//遍历检查是否有以该结点为父结点的结点
for (int j = 0; j < sz; ++j)
{
if (j == i) // 跳过自身
continue;
// 如果有以该结点为父结点的结点,则该结点不是叶结点
if (tree->nodes[j].parent == i)
{
isleaf = false;
break;
}
}
if (isleaf)
cout << tree->nodes[i].data << " ";
}
cout << endl;
}完整代码
#include
#include
#include
using namespace std;
const int MAX_SIZE = 102;
struct Node
{
char data;
int parent;
};
struct Tree
{
Node nodes[MAX_SIZE];
int size;
};
Tree *CreateTree()
{
Tree *tree = (Tree *)malloc(sizeof(Tree));
memset(tree->nodes, 0, sizeof(tree->nodes));
const char def_data[] = {'R', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'K'};
const int def_parent[] = {-1, 0, 0, 0, 1, 1, 3, 6, 6, 6};
const int sz = 10;
for (int i = 0; i < sz; ++i)
{
Node &node = tree->nodes[i];
node.data = def_data[i];
node.parent = def_parent[i];
}
tree->size = sz;
return tree;
}
void DelTree(Tree *tree)
{
delete tree;
}
void Print(Tree *tree)
{
if (tree->size == 0)
return;
cout << "data parent" << endl;
for (int i = 0; i < tree->size; ++i)
cout << tree->nodes[i].data << " " << tree->nodes[i].parent << endl;
}
int GetHeight(Tree *tree)
{
int maxh = 0;
for (int i = 0; i < tree->size; ++i)
{
Node *node = &tree->nodes[i];
int h = 1;
while (node->parent != -1)
{
node = &tree->nodes[node->parent];
++h;
}
maxh = max(maxh, h);
// cout << tree->nodes[i].data << ": " << h << endl;
}
return maxh;
}
void PrintAllLeaves(Tree *tree)
{
int sz = tree->size;
if (sz == 0)
return;
cout << "Leaves: ";
for (int i = 0; i < sz; ++i)
{
bool isleaf = true;
for (int j = 0; j < sz; ++j)
{
if (j == i)
continue;
if (tree->nodes[j].parent == i)
{
isleaf = false;
break;
}
}
if (isleaf)
cout << tree->nodes[i].data << " ";
}
cout << endl;
}
int main()
{
Tree *tree = CreateTree();
Print(tree);
cout << "Height: " << GetHeight(tree) << endl;
PrintAllLeaves(tree);
DelTree(tree);
return 0;
} 本文到此结束。