手刻 Deep Learning -第壹章-PyTorch入门教学-基础概念与再探线性回归

一、前言

        本章会需要 微分、线性回归与矩阵的基本观念

        这次我们要来做 PyTorch 的简单教学，我们先从简单的计算与自动导数（ auto grad / 微分 ）开始，使用优化器与误差计算，然后使用 PyTorch 做线性回归，还有 PyTorch 于 GPU 显示卡（ CUDA ） 的使用范例。

本文的重点是学会 loss function 与 optimizer 使用

文本目录 ：

• 为什么选择 PyTorch？
• 名词与概念介绍 导数（partial derivative）， 优化器（optimizer）， 损失函数 （ loss function ）
• 自动导数 /Auto grad （手工优化与损失函数的实作）<- 此节很无聊
• 优化器， 损失函数， 矩阵与 partial derivative 示例
• 线性回归与矩阵范例 —Model 概念
• GPU 显卡 （CUDA） 运算范例

本文不讲解如何安装 PyTorch ，且假设读者已经拥有 Numpy 使用经验
如果手边没有环境，可以使用 Google Colab （ Google 已经帮各位安装好许多常用的套件 ）

二、选择 PyTorch的理由

        Machine Learning / Deep Learning 有许多 Framework 可以使用，其中 Keras （Tensorflow） 与 PyTorch 本人都有使用经验，但如果想要研究与了解 Deep Learning 如何运作，本人认为最好的方式是使用 PyTorch

        一般使用 Keras （Tensorflow） 虽然可以快速的建立模型，但是底层原理没有打好基础的人一定会是雾里看花

知其然，知其所以然

        PyTorch 使用上很接近 Numpy，另外有强大的数学计算功能，例如：自动微分，自动优化，方便配置到显卡上运算 （Nvidia CUDA，而且就本人使用经验来说，安装比 TensorFlow 容易 ）... 如果知道 PyTorch 这些功能，可以使用在各种数学应用，而且对于 Machine Learning / Deep Learning 底层运作也会更加了如指掌

三、名词与概念介绍 导数（partial derivative）， 优化器（optimizer）， 损失函数 （ loss function ）

其实我们之前的章节，就是在为这些铺路

3.1 损失函数 （ loss function ）

        这个名词中文看来奇怪，其实他是计算数值差距用的，计算与答案的误差，帮助我们找目标的公式，例如：
我们有 18 元去买 3块钱的苹果，我们只买了 5颗，我们是不是还可以买更多 ？ （ 18–3*5=3，我们剩下 3元 ，误差就是 3 ）
在线性回归 中就是计算和答案的差距，主要用来取得导数

3.2 导数（ partial derivative）

就是微分概念，透过损失函数还可以找出我们要移动的方向和距离

3.3 优化器 （ optimizer ）

        开始修正我们的数值使用，也有人称优化器，就是依靠导数去调整数值

        导数部分其实不用特别关心，他实务上隐藏在 loss function 与 optimizer 之间，但是这三者的组合就是 Machine Learning 中常用的概念
流程就是

误差计算 -> 寻找导数 -> 优化 ->误差计算 -> 寻找导数 -> 优化 ->误差计算 -> 寻找导数 -> 优化 ->误差计算 -> 寻找导数 -> 优化 ->...

四、自动导数 / Auto grad （ 手工优化与损失函数的实现）

先说此节很无聊， 是介绍损失函数与优化器如何运作，但是可以跳到下节没关系

本节承接 线性回归 概念，一样依照 loss function 与 optimizer 架构

微分在 Machine Learning 中是非常重要的计算，而这种计算已经有公式可循，所以 PyTorch 会自动的帮我们计算（也就是我们之前章节说过，不会算没关系，电脑可以帮我们算），但是概念与原理要懂

这边的 grad 其实就是微积分中的 partial derivative （导数 / 斜率），PyTorch 会帮我们追踪每个变量的 导数/斜率 ，即自动追踪变量的任何变化

现在我们来看最基础的 PyTorch 与 Auto grad 范例 ：
假设今天在商场买苹果结账，假设苹果 3 元，我们手上有 18 元，纸袋 不用钱（这边为了方便范例先忽略） ，我们要去尽可能的买越多苹果越好
公式如下：

结账总额（Y） = 苹果数量（a） * 苹果单价（X） + 纸袋单价（b）
换成数学公式是 Y = aX + b

• Y 是我们手上有的钱，这个我们不能改变
• X 是苹果单价，这个我们不能改变
• a 是苹果数量，这是我们要找出来的
• b 这边因为纸袋0元，所以我们直接省略不看

x = torch.tensor([3.0])  # 蘋果單價
y = torch.tensor([18.0]) # 我們的預算
a = torch.tensor([1.0], requires_grad=True)  # 追蹤導數
print('grad:', a.grad)
loss = y - (a * x)  # loss function ( 中文稱 損失函數 )
loss.backward()
print('grad:', a.grad)

解说：

• torch.tensor： 就是建立一个 Tensor （类似于 np.array ）
• requires_grad=True 我们有需要追踪的变量才要加上这个参数，不用追踪的不用，例如这个范例中我们只希望 a 改变，不要去动其他数值，所以只有 a 有 requires_grad=True

4.1 损失函数（ loss function）

实务上是让他越接近 0 越好，我们后面会套用 PyTorch 内建的 function ，就不用每次的手工打造

• 上面代码中，loss就是差价公式，概念就是Y= ax + b，但是我们的目标是要把钱花光光，所以loss要越趋近于0越好
  所以数学上就成了Y-（ax + b） = 0是我们的目标
• loss.backward（） 就是和 PyTorch 说开始反向追踪

这是 print 出来的结果

# grad: None
# grad: tensor([-3.])

可以看到我们 print（'grad：'， a.grad） ，在 loss.backward 之前是没有数值的
但是之后冒出一个 -3，这个 -3 就是 partial derivative （会微积分的人可以算看看 ），然后我们可以靠这个数值去调整 a 的值，如下

4.2 优化器

PyTorch 有内建好的优化器，但是我们这边为了演示原理，一样手工计算 （下节我们会使用内建的）
下面代码是我们开始进行线性回归优化 （ 计算 100 次 ）

for _ in range(100):
    a.grad.zero_()
    loss = y - (a * x)
    loss.backward()
    with torch.no_grad():
        a -= a.grad * 0.01 * loss

解说：

• 每一次的 backward ，a 的 grad 都会相加，所以我们要先做归零
  （就像是实验室仪器每次都要先归零校正 ）
• loss 与 loss.backward 上面已经解说过，用来反向追踪导数
• with torch.no_grad（）： 这部分概念很重要，前面提过 PyTorch 会自动追踪 a 的任何计算，所以我们手动调整 a 一定要和 PyTorch 说，不要追踪我们的手动调整

我們看看跑 100 次迴歸的結果

損失函跑 100 次的變化

print('a:', a)
print('loss:', (y - (a * x)))
print('result:', (a * x))
# a: 5.999598503112793
# loss: 0.0012054443359375
# result: 17.998794555664062

可以看到 a 趋近于 6， 误差 （loss ） 趋近于 0
表示我们真的可以用 18 块钱去买 6 颗苹果 3元的苹果

五、优化器， 损失函数， 矩阵与 partial derivative 示例

        这边我们要用 PyTorch 内建的 loss function 与 optimizer 来做计算，会方便很多，而且可以做更多复杂的问题

本文的重点是学会 loss function 与 optimizer 使用

        直接看代码（一样是苹果 3元范例 ）

x = torch.tensor([3.0])
y = torch.tensor([18.0])
a = torch.tensor([1.0], requires_grad=True)
loss_func = torch.nn.MSELoss()
optimizer = torch.optim.SGD([a], lr=0.01)
for _ in range(100):
    optimizer.zero_grad()
    loss = loss_func(y, a * x)
    loss.backward()
    optimizer.step()

解说：

• loss_func 就是损失函数，我们这边使用 torch.nn.MSELoss
  他其实是计算 均方误差，loss function 有很多种，我们日后有机会再介绍，但是这边要知道很多情况下的数值比较其实用 MSELoss 就很好用了
  细节：https://pytorch.org/docs/stable/nn.html#loss-functions
• optimizer 就是优化器
  torch.optim.SGD（[a]， lr=0.01） 这边是我们使用 SGD ，一样优化器有很多种，我们这边为了简单示范先用 SGD
  -> [a] 是我们和优化器说照顾好我们的 a 变量
  -> lr 是学习率， 数值都是小于 1，实际看场合调整， 我们这边 0.01 是为了快速示范
  细节 ： torch.optim — PyTorch 2.0 documentation
• optimizer.zero_grad 是为了归零调整，因为每次 backward 都会增加 grad 的数值（就像是实验室每次做实验都要归零调整，不然上个用户的操作会干扰实验结果 ）
• loss.backward（） 做反向传导，就是找出导数
• optimizer.step 告诉优化器做优化，他会自动帮我们调整 a 的数值

        我们测试一下矩阵概念的计算
        假设一样是 18 元的预算，三个种不同的苹果
        售价分别是 3 元， 5 元， 6 元，这样可以买几颗 ？

        我们只要修改一下数值

x = torch.tensor([3.0, 5.0, 6.0,])   # 不同種蘋果售價
y = torch.tensor([18.0, 18.0, 18.0]) # 我們的預算
a = torch.tensor([1.0, 1.0, 1.0], requires_grad=True) # 先假設都只能買一顆

        然后我们跑计算 （ 这里跑 1000 次，让数值精准些 ）

loss_func = torch.nn.MSELoss()
optimizer = torch.optim.SGD([a], lr=0.01)
for _ in range(1000):
    optimizer.zero_grad()
    loss = loss_func(y, a * x)
    loss.backward()
    optimizer.step()
print('a:', a)
# a: tensor([6.0000, 3.6000, 3.0000], requires_grad=True)

        看起来没错，如果只有 18 元，分别去买不同的苹果，我们只能买 6 颗 （ 3元 ）， 3 颗（5元）， 3 颗（6元）

六、线性回归与矩阵范例 —Model 概念

有了上面的概念，现在我们来做更进阶的范例

data -> model -> output

我们将输入数据到输出数据这个过程称为 “Model” ，概念上就是可以当作是一个黑箱，我们把数据丢进去 （一般称为 X ），就会产生出预测数据 （ 称为 Y ），例如：

• 影像分类：照片丢入 model ，然后 model 告诉我们影像的类别
• 资料预测：过去几天的气象资料（温度、湿度、气压.. . ） 丢入 model ，然后得到几天后的预测
• 语音识别：用户说话的音频丢入 model ，得到文字输出

6.1 准备资料

        因为本文是在示范线性回归，我们先不探讨复杂问题，先做最简单的计算，所以这次我们使用 sklearn 来产生假资料练习
（打好基础比较重要）

from sklearn.datasets import make_regression
np_x, np_y = make_regression(n_samples=500, n_features=10)
x = torch.from_numpy(np_x).float()
y = torch.from_numpy(np_y).float()

        np_x 是产生出来的测试线性回归数据，有 10 个不同的属性，500 笔数据（可以使用 np_x.shape 看到 ）
        np_y 是产生出来的答案

        因为， make_regression 产生出来的是 numpy，他不是 PyTorch 的 Tensor，所以我们要转换一下 （ torch.from_numpy（... ）. float() )

6.2 建立我们的 Model

w = torch.randn(10, requires_grad=True)
b = torch.randn(1, requires_grad=True)
optimizer = torch.optim.SGD([w, b], lr=0.01)
def model(x):
    return x @ w + b

解说：

• w：就是乱数产生的“权重”，我们会用矩阵计算将 x 的每个特征相乘，记得我们上面产生的数据有 10 个特征吗？ 所以他是 torch.randn（10），而 requires_grad=True 就是和 PyTorch 说我们要优化这个数值
• b：源自于 y=aX + b 公式，这次我们把 b 放进来了
• torch.optim.SGD（[w， b]， lr=0.01） 就是优化器，和他说明我们要追踪 w 和 b

再来 model function 就是我们这次的主角，基本精神就是 y=aX + b （这边的 a 我们已经改用 w 替代 ）

6.3 先预测

我们还没有训练我们的 model ，先看直接丢入 数据 （x） 会生出什么

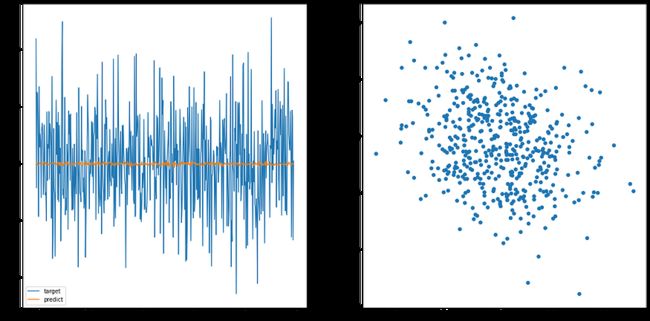
predict_y = model(x)

然后我们可视化一下

plt.figure(figsize=(20, 10))
plt.subplot(1, 2, 1)
plt.plot(y)
plt.plot(predict_y.detach().numpy())
plt.subplot(1, 2, 2)
plt.scatter(y.detach().numpy(), predict_y.detach().numpy())

什么都不训练，直接预测

        说明一下，左图是数据范围，理想上两个颜色的线应该会看起来一致; 右图是数据预测与目标数据的分布图，理想上应该要是一条直线（左右到右上），看我们之后训练过的 model 就可以知道差异

6.4 开始训练

        直接看程序

loss_func = torch.nn.MSELoss() # 之前提過的 loss function 
history = []   # 紀錄 loss（誤差/損失）的變化
for _ in range(300):   # 訓練 300 次
    predict_y = model(x)
    loss = loss_func(predict_y, y)
    # 優化與 backward 動作，之前介紹過
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    history.append(loss.item())
plt.plot(history)

loss history

        可以看到 loss 随时间降低，这表示我们的 model 确实有学到东西，再来看看预测结果

predict_y = model(x)
plt.figure(figsize=(20, 10))
plt.subplot(1, 2, 1)
plt.plot(y, label='target')
plt.plot(predict_y.detach().numpy(), label='predict')
plt.legend()
plt.subplot(1, 2, 2)
plt.scatter(y.detach().numpy(), predict_y.detach().numpy())

预测结果

        如上所言，我们输入 x 到 model ，可以得到很好的 y （ 预测与答案几乎相似）

七、GPU 显卡 （CUDA） 运算范例

        之前的其他文章提过， 显示卡对于矩阵计算非常在行
        而 PyTorch 对于使用显卡计算很容易，如果读者是 Nvidia 显卡用户，安装 CUDA 相关套件即可（这部分就不在本文教学范围了），而 AMD 用户，听说有 AMD ROCm 可以使用，不过本人没有使用过也不清楚（本人手上都是老黄牌的显卡）

        我们要在 PyTorch 使用 cuda ，先检测一下环境支不支持

torch.cuda.is_available()

        看到结果是true，表示应该（可能？ 或许？ 大概？ ）没有问题（ 因为实际上可能会有 CUDA 版本 / 驱动 各种奇怪状况）

        再来就是我们把 device 抓出来

device = torch.device('cuda')    # cuda 即 nvidia gpu 計算
#  device = torch.device('cpu')  # 如果想回到 cpu 計算

再来，为了我们要示范GPU和CPU的差异，我们需要更多数据

from sklearn.datasets import make_regression
np_x, np_y = make_regression(n_samples=5000, n_features=5000)
x = torch.from_numpy(np_x).float().to(device)
y = torch.from_numpy(np_y).float().to(device)

        为了要让矩阵更大，所以我们这次增加到5000个特征
        然后注意上面的to（device）这就是把 PyTorch 的 Tensor 搬移到设备上面（我们已经指定成 cuda ），所以这些资料已经被移动到 GPU 上

只有位在相同的设备的 Tensor 才能互相计算，例如 gpu 只能算 gpu，cpu 只能算 cpu，所以计算之前要 .to（device） 到相同设备

        现在我们建立 model （这个 model 我们要移动到 GPU 上）

w = torch.randn(5000).to(device)
b = torch.randn(1).to(device)
w.requires_grad=True
b.requires_grad=True
optimizer = torch.optim.SGD([w, b], lr=0.01)
def model(x):
    x = x @ w + b
    return x

一样的 to（device），然后 requires_grad 是因为移动到 GPU 上已经不同于 CPU，所以我们要另外设置要求追踪导数 （ 优化器这些就一样的代码）

再来跑训练

loss_func = torch.nn.MSELoss()
history = []
ts = time.time()
for _ in range(1000):   # 訓練 1000 次
    predict_y = model(x)
    loss = loss_func(predict_y, y)
    # 優化與 backward 動作
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    history.append(loss.item())
print(f'run_time: {time.time()-ts:.5f}')
plt.plot(history)

我們另外加了 time.time 來看執行時間

以下是本人的一些紀錄

• AMD 3900X (CPU): 2.8 sec
• Nvidia 3090(GPU) : 0.327 sec
• Jetson Nano 4GB (CPU): 52.7 sec
• Jetson Nano 4GB (GPU):16.47 sec

         如果是影像處理(CNN)或是隨 model 複雜度增加，時間差距會更大，另外也看到 GPU 的 RAM 被佔用

gpu ram 被使用

        这也是为什么 Deep Learning 会需要大内存显卡的原因，当你越多的数据搬移到 GPU 就会需要更多空间

八、结语

本文的重点是学会 loss function 与 optimizer 使用

        其实掌握正确的 loss function 与 optimizer，在 model 的设计上就会顺利很多，这个我们日后有机会介绍会看到，另外本文其实很多观念与细节碍于篇幅与时间没有很详细的交代

        如果有兴趣的读者可以自行输入代码与试验不同的数值，去发现其中的细节变化，熟悉这些操作与概念对于 Machine Learning / Deep Learning 会很有帮助Seachaos