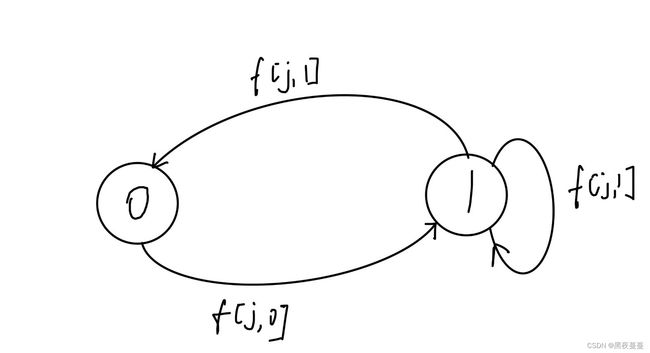
树形DP+状态机
一、战略游戏
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。他必须保护一座中世纪城市,这条城市的道路构成了一棵树。每个节点上的士兵可以观察到所有和这个点相连的边。他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
例如,下面的树:
只需要放置 1名士兵(在节点 1处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。对于每组测试数据,第一行包含整数 N,表示树的节点数目。
接下来 N行,每行按如下方法描述一个节点。节点编号:(子节点数目) 子节点 子节点 …节点编号从 0到 N−1,每个节点的子节点数量均不超过 10,每个边在输入数据中只出现一次。
输出格式
对于每组测试数据,输出一个占据一行的结果,表示最少需要的士兵数。
数据范围
0
输入样例:
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
输出样例:
1
2
分析:
1、每一条边都需要有人看住,即一条边的两点中至少有一个点需要有人
2、f[u][2]:
f[u][0]:表示节点u不放人时所需的是士兵数
f[u][1]:表示节点u放人时所需的是士兵数
3、要求最小值
4、转移方程:
f[u][0]+=f[j][1]
f[u][1]+=min(f[j][0],f[j][1])
//若父节点有人,子节点均可
状态机
AC
#include
#include
#include
using namespace std;
int n;
int h[1600],e[1600],ne[1600],idx;
bool st[1600];
int f[1600][2];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][0]=0;
f[u][1]=1;
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
dfs(j);
f[u][0]+=f[j][1];
f[u][1]+=min(f[j][0],f[j][1]);
}
}
int main()
{
while(cin>>n)
{
memset(h,-1,sizeof h);
memset(e,0,sizeof e);
memset(ne,0,sizeof ne);
memset(st,0,sizeof st);
memset(f,0,sizeof f);
idx=0;
for(int l=1;l<=n;l++)
{
int x;
int m;
scanf("%d:(%d)",&x,&m);
//cout< 二、皇宫看守
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。
已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入中数据描述一棵树,描述如下:
第一行 n,表示树中结点的数目。第二行至第 n+1行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 i,在该宫殿安置侍卫所需的经费 k,该结点的子结点数 m,接下来 m 个数,分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。对于一个 n个结点的树,结点标号在 1 到 n之间,且标号不重复。
输出格式
输出一个整数,表示最少的经费。
数据范围
1≤n≤1500
输入样例:
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
输出样例:
25
样例解释:
在2、3、4结点安排护卫,可以观察到全部宫殿,所需经费最少,为 16 + 5 + 4 = 25。
分析
1、本题不同于上一题,是对点的限制
2、对于某个点有三种情况
f[u][0]:点u被父节点看到,点u未放守卫
f[u][1]:点u被子节点看到,点u未放守卫
f[u][2]:点u被自己看到3、具体见代码注释
#include
#include
#include
using namespace std;
const int N=1510,INF=0x3f3f3f;
int n;
int h[N],e[N],ne[N],idx;
int w[N];
bool st[N];
int res=INF;
int f[N][3];
/*
f[u][0]:点u被父节点看到,点u未放守卫
f[u][1]:点u被子节点看到,点u未放守卫
f[u][2]:点u被自己看到
*/
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
f[u][0]=0;
f[u][2]=w[u];
int sum=0;//sum即f[u][0],表示当前节点不放人,其所有子节点的花费的和的最小值
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
dfs(j);
//节点u被其父节点看住,则其子节点由自己看住,或者被子节点的子节点看住
f[u][0]+=min(f[j][1],f[j][2]);
//节点u被自己看住,则其子节点选择三种情况均可
f[u][2]+=min(min(f[j][0],f[j][1]),f[j][2]);
sum+=min(f[j][1],f[j][2]);
}
/*
f[u][1]:节点u被其子节点看住,需要选择有哪个子节点看住,所有子节点均可
sum:存下u的所有子节点选择由自己看住或者由自己的子节点看住所需要的最小花费
求f[u][1]即:枚举妻子节点,将sum减去该子节点的花费(选择由自己看住或者由自己的子节点看住
不确定,所以根据sum的求法需要减去min(f[j][1],f[j][2])),再选择该节点由自己
看住自己,加上其花费
*/
f[u][1]=INF;
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
f[u][1]=min(f[u][1],sum-min(f[j][1],f[j][2])+f[j][2]);
//等价于:f[u][1]=min(f[u][1],f[u][0]-min(f[j][1],f[j][2])+f[j][2])
}
}
int main()
{
cin>>n;
memset(h, -1, sizeof h);
for(int i=1;i<=n;i++)
{
int x,cost,m;
scanf("%d%d%d",&x,&cost,&m);
w[x]=cost;
for(int j=1;j<=m;j++)
{
int u;
scanf("%d",&u);
add(x,u);
st[u]=true;
}
}
int root=1;
while(st[root]) root++;
dfs(root);
cout<