【计算机视觉】计算机视觉与深度学习-05-纹理表示&卷积神经网络-北邮鲁鹏老师课程笔记
计算机视觉与深度学习-05-纹理表示&卷积神经网络-北邮鲁鹏老师课程笔记
- 纹理表示&卷积
-
- 纹理定义
- 纹理分类
-
- 1 规则纹理
- 2 随机纹理
- 纹理表示步骤
- 纹理表示方法
-
- 基于卷积核组的纹理表示
-
- 1 步骤一:设计卷积核组
-
- 卷积核类型(边缘、条形、点状)
- 卷积核尺度(3~6个尺度)
- 卷积核方向(6个角度)
- 2 步骤二:获取图像中基元
- 3 步骤三:用基元表示纹理
-
- 表示方式一(含基元位置信息)
- 表示方式二(忽略基元位置信息)(常用)
- 纹理表示案例
- 纹理表示注意事项
- 纹理表示与卷积神经网络的联系
- 全连接神经网络
-
- 全连接神经网络的瓶颈 - 参数过多易过拟合&显存压力大
- 全连接神经网络应用场景
- 卷积神经网络
-
- 卷积层
-
- 卷积核
- 卷积操作
- 卷积层设计
- 边界填充
- 特征响应图组尺寸计算
- 池化层
-
- 池化操作定义
- 池化操作作用
-
- 减少后续卷积层计算量
- 缩小特征响应图像 & 增大感受野
- 池化层超参数
-
- 池化窗口
- 池化步长
- 常见池化操作
-
- 最大池化
- 平均池化
- 池化操作示例
- 全连接层
- 样本增强
- ImageNet & ILSVRC
- 经典网络解析
-
- LeNet5
- AlexNet
-
- 参考
- 代码
- AlexNet模型结构
-
- 第一层 卷积层1
-
- 输入
- 卷积
- 局部响应归一化层(Local Response Normalized)
-
- 为什么要引入LRN层?
- 归一化有什么好处?
- 池化
- 第二层 卷积层2
- 第三层 卷积层
- 第四层 卷积层
- 第五层 卷积层
- 第六层&第七层&第八层 全连接层
- 重要说明
- 重要技巧
- AlexNet卷积层在做什么?
- ZFNet
-
- 参考
- 主要改进
-
- 改进一:减小第一层卷积核
- 改进二:减小第一层卷积步长
- VGG16
-
- VGG贡献
- 网络结构
- 主要改进
-
- 输入去均值
- 小卷积核串联代替大卷积核
- 无重叠池化
- 卷积核个数逐层增加
- GoogLeNet
-
- GoogLeNet模型结构
- 数据预处理
- 创新点
-
- Inception结构
- 平均池化+去除两个全连接层
- 辅助分类器
- 思考
-
- 问题1 :平均池化向量化与直接展开向量化有什么区别?
- 问题2: 利用1 x1卷积进行压缩会损失信息吗?
- ResNet
-
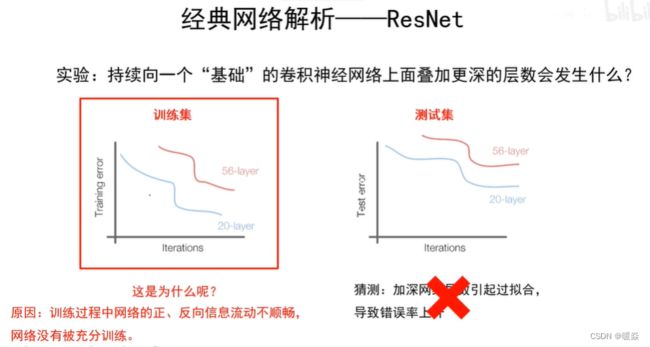
- 产生背景
- 贡献
-
- 残差模块
-
- 为什么残差网络性能好?
- 批归一化
- 针对ReLU的初始化方法
- 小结
纹理表示&卷积
纹理定义
计算机图形学中的纹理既包括通常意义上物体表面的纹理即使物体表面呈现凹凸不平的沟纹,同时也包括在物体的光滑表面上的彩色图案,通常我们更多地称之为花纹。
纹理是由于物体表面的物理属性的多样性而造成的,物理属性不同表示某个特定表面特征的灰度或者颜色信息不同,不同的物理表面会产生不同的纹理图像,因而纹理作为图像的一个极为重要的属性,在计算机视觉和图像处理中占有举足轻重的地位。纹理是图像中特征值强度的某种局部重复模式的宏观表现。然而,对于自然纹理图像而言这种重复模式往往是近似的和复杂的,难以用语言描述,而人类对纹理的感受多是与心理效果相结合的,因此,迄今都没有一个对纹理的正式的、广泛认可的和一致的定义。
Hawkins曾经对纹理给出了一个比较详细的描述,他认为纹理有三个主要的标志:
1)某种局部的序列性在比该序列更大的区域内不断重复
2)序列是由基本元素非随机排列组成的
3)各部分大致是均匀的统体,在纹理区域内的任何地方都有大致相同的结构尺
纹理分类
![]()
1 规则纹理
2 随机纹理
自然界中,一般都是随机纹理。
纹理表示步骤
步骤一:设计卷积核组。
步骤二:利用卷积核组提取图像中的纹理基。
步骤三:利用基元的统计信息来表示图像中的纹理。
纹理表示方法
基于卷积核组的纹理表示
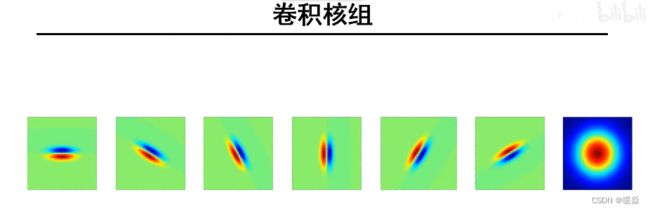
1 步骤一:设计卷积核组
卷积核组又称为纹理滤波器组。
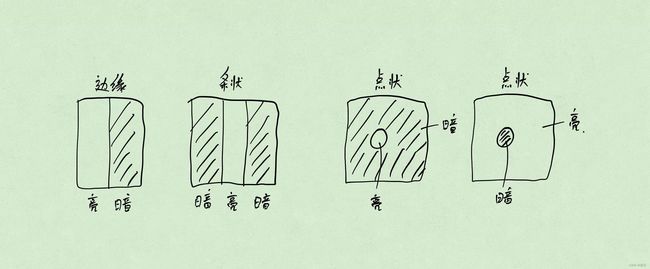
卷积核类型(边缘、条形、点状)
边缘:高斯一阶偏导核。例:黑|白,白|黑。
条形:高斯二阶偏导核。例:白|黑|白,黑|白|黑。
点状:。例:周围白中间黑,周围黑中间白。
卷积核尺度(3~6个尺度)
大尺度,提取粗粒度边。
小尺度,提取细粒度边。
卷积核方向(6个角度)
前6个卷积核检测是否存在边缘及边缘的方向。
第1个卷积核检测图像中是否有x方向的边缘。(高斯卷积核对y求导)
第4个卷积核检测图像中是否有y方向的边缘。(高斯卷积核对x求导)
第7个卷积核检测图像中是否有斑状基元。
2 步骤二:获取图像中基元
特征响应图中包含了图像的纹理基元。
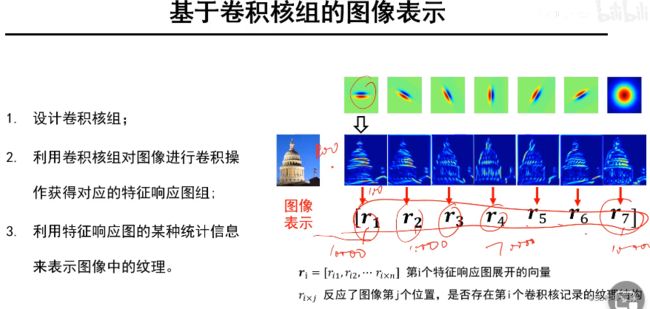
3 步骤三:用基元表示纹理
利用特征响应图的某种统计信息来表示图像中的纹理。
表示方式一(含基元位置信息)
假设图片是100*100,使用上述含7个卷积核的卷积核组,则该图片每一个像素点表示为 r i = [ r i 1 , r i 2 , r i 3 , r i 4 , r i 5 , r i 6 , r i 7 ] , r i − m a x = m a x { r i 1 , r i 2 , r i 3 , r i 4 , r i 5 , r i 6 , r i 7 } r_i=[r_{i1},r_{i2},r_{i3},r_{i4},r_{i5},r_{i6},r_{i7}],r_{i-max}=max\{r_{i1},r_{i2},r_{i3},r_{i4},r_{i5},r_{i6},r_{i7}\} ri=[ri1,ri2,ri3,ri4,ri5,ri6,ri7],ri−max=max{ri1,ri2,ri3,ri4,ri5,ri6,ri7}。则 r i − m a x r_{i-max} ri−max 对应的特征响应图即为该像素点的特征。
其中r_{i}的维度是 10000 ∗ 1 10000*1 10000∗1, [ r 1 , r 2 , r 3 , r 4 , r 5 , r 6 , r 7 ] [r_{1},r_{2},r_{3},r_{4},r_{5},r_{6},r_{7}] [r1,r2,r3,r4,r5,r6,r7]的维度是 10000 ∗ 7 10000*7 10000∗7,经过变换后 [ r 1 , r 2 , r 3 , r 4 , r 5 , r 6 , r 7 ] [r_{1},r_{2},r_{3},r_{4},r_{5},r_{6},r_{7}] [r1,r2,r3,r4,r5,r6,r7]的维度为70000*1。
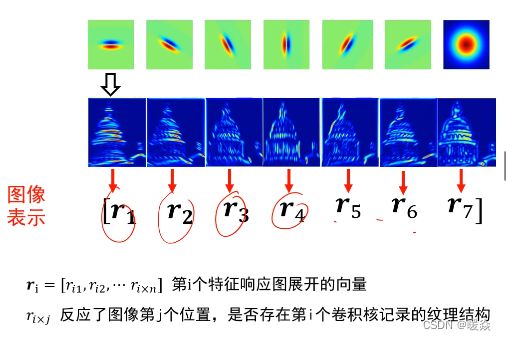
该表示方式的缺点:70000维太复杂。
表示方式二(忽略基元位置信息)(常用)
纹理分类任务中,基元的位置对纹理分类没有影响,只关注出现了哪种基元对应的纹理以及基元出现的频率,即用特征响应图的平均值表示图像。
假设图片是100*100,使用上述含7个卷积核的卷积核组,则该图片每一个像素点基元平均值表示为 r ‾ = [ r ‾ 1 , r ‾ 2 , r ‾ 3 , r ‾ 4 , r ‾ 5 , r ‾ 6 , r ‾ 7 ] , r ‾ i − m a x = m a x { r ‾ 1 , r ‾ 2 , r ‾ 3 , r ‾ 4 , r ‾ 5 , r ‾ 6 , r ‾ 7 } \overline{r}=[\overline{r}_1,\overline{r}_2,\overline{r}_3,\overline{r}_4,\overline{r}_5,\overline{r}_6,\overline{r}_7],\overline{r}_i-max=max \{\overline{r}_1,\overline{r}_2,\overline{r}_3,\overline{r}_4,\overline{r}_5,\overline{r}_6,\overline{r}_7 \} r=[r1,r2,r3,r4,r5,r6,r7],ri−max=max{r1,r2,r3,r4,r5,r6,r7}。则 r ‾ i − m a x \overline{r}_{i-max} ri−max对应的特征响应图即为该像素点的特征。
其中 r ‾ i 为第 i 个特征响应图的平均值,其维度是 1 ∗ 1 , r ‾ j 的维度是 1 ∗ 7 ,经过变换后 r ‾ j 的维度为 7 ∗ 1 其中\overline{r}_i为第i个特征响应图的平均值,其维度是1*1,\overline{r}_j的维度是1*7,经过变换后\overline{r}_j的维度为7*1 其中ri为第i个特征响应图的平均值,其维度是1∗1,rj的维度是1∗7,经过变换后rj的维度为7∗1。
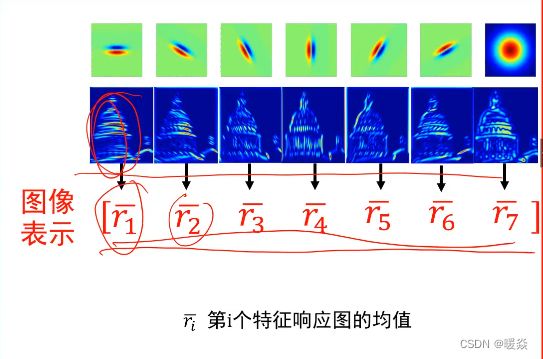
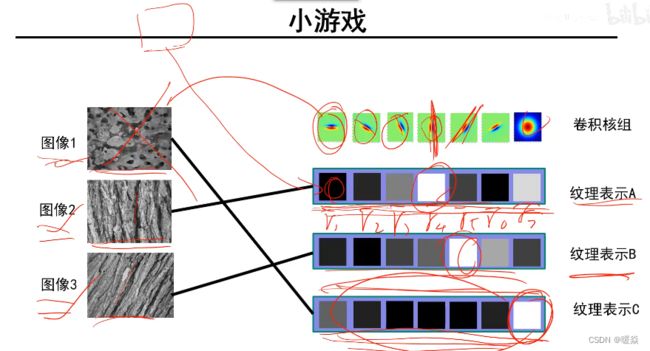
纹理表示A:r4 比较大,表示y方向的纹理比较多。
纹理表示B:r5 比较大,表示y=x方向的纹理比较多。
纹理表示C:r7 比较大,表示斑点纹理比较多。
纹理表示案例
纹理表示注意事项
r ‾ = [ r ‾ 1 , r ‾ 2 , r ‾ 3 , r ‾ 4 , . . . , r ‾ 46 , r ‾ 47 , r ‾ 48 ] \overline{r}=[\overline{r}_1,\overline{r}_2,\overline{r}_3,\overline{r}_4,...,\overline{r}_{46},\overline{r}_{47},\overline{r}_{48}] r=[r1,r2,r3,r4,...,r46,r47,r48] 中最大值大概率只有一个,因为一张图像包含一个卷积核组所表示的纹理的概率大,包含多个卷积核组所表示纹理的概率很小,所以这个48维向量是稀疏向量。
纹理表示与卷积神经网络的联系
从纹理表示中的卷积核组理解卷积神经网络的卷积层,神经网络中卷积核可能比上例中纹理表示的卷积核更复杂。神经网络的卷积层可以看做上例中纹理表示卷积核组的扩展。
全连接神经网络
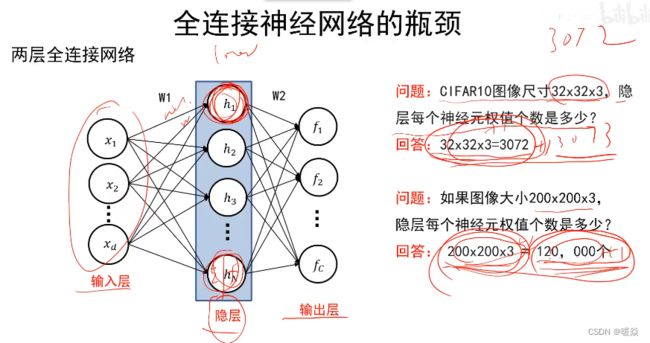
全连接神经网络的瓶颈 - 参数过多易过拟合&显存压力大
假设图像尺寸为 200 ∗ 200 ∗ 3 200*200*3 200∗200∗3,则输入层神经元个数 d 为120000个,对于全连接神经网络,后一层的每个神经元都会与前一层的所有神经元相连,所以隐层每个神经元就有120000个权值,再加一个偏置值。
如果每个隐层有1000个神经元,则每个隐层就有120000*1000个权值。
参数越多,模型越容易过拟合。
参数越多,计算量越大。
前向传播数据需要存入显存,参数越大,显存压力越大。
全连接神经网络应用场景
全连接神经网络仅适合参数少的情况,例如:处理小图像。或者前置输出已经表示为向量的场景,例如:接在卷积神经网络之后对cnn得到的特征(该处的特征可以类比纹理表示中的48维向量)进行处理。
卷积神经网络
可以将卷积神经网络类比为纹理表示例子中的卷积核组,最后得到表示特征响应图组的48维向量,之后接全连接神经网络进行分类(全连接神经网络适合处理小输入)。

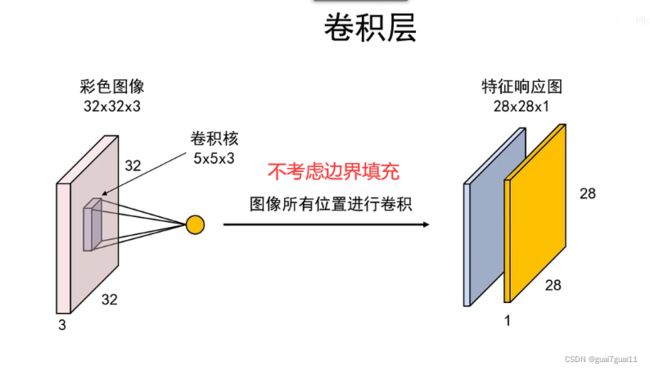
卷积层
卷积核
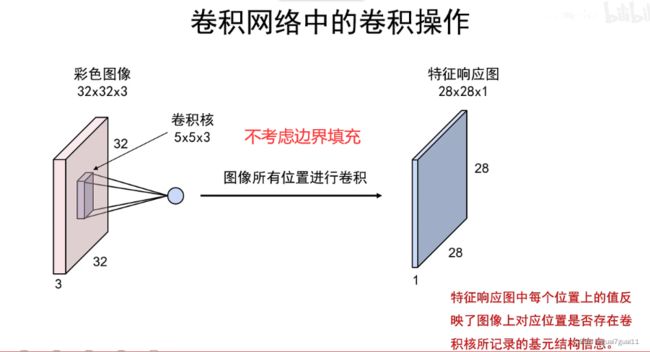
卷积操作
卷积层设计
卷积核深度 = 前一层图像的深度(前层决定,不是自定义)
卷积核个数 = 自己自定义
特征图个数 = 卷积核个数
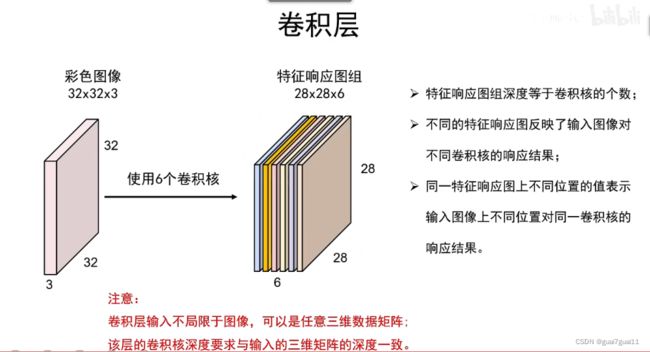
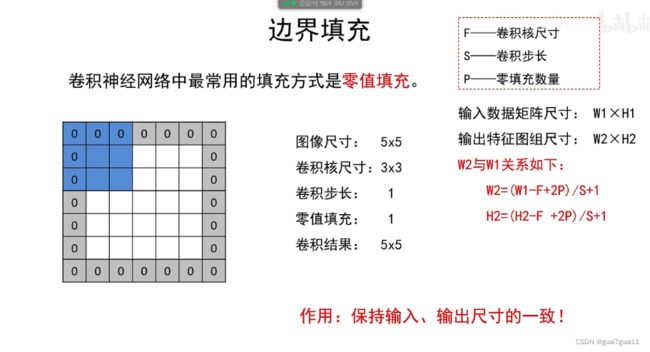
边界填充
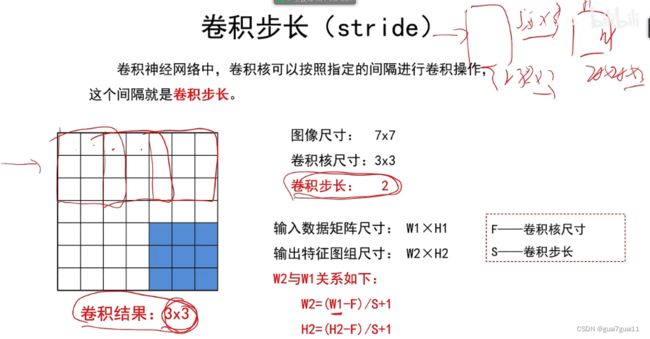
特征响应图组尺寸计算
卷积核尺寸,卷积步长,填充数量,以及卷积核数量最好经过周密的设计,到自己输出层时正好是自己需要的尺寸,最好不要中间出现除不尽的情况,如果出现除不尽的情况,就忽略几个像素。
池化层
池化操作定义
对特征响应图某个区域进行池化就是在该区域上指定一个值来代表整个区域。
池化操作对每个特征响应图独立进行。
池化操作作用
对每一个特征响应图独立进行,降低特征响应图组中每个特征响应图的宽度和高度,减少后续卷积层的参数的数量,降低计算资源耗费,进而控制过拟合。
卷积运算复杂度O(km2n2 ),其中k为卷积核个数,m为卷积核边长,n为图像边长。
减少后续卷积层计算量
神经网络中为了反向计算梯度,需要在显存中保存前向计算结果。
如果卷积之后特征响应图和原图像的长宽相同,卷积核多的情况下,特征响应图组的层数增多,需要保存的数据就变多。可能超出显存存储能力范围。
池化操作可以减少特征响应图的长宽,达到减少计算量的效果。
缩小特征响应图像 & 增大感受野
卷积核的尺寸相对变大,粗粒度提取,使得卷积核在图像上的视野更广,即感受野更大,可以提取更多信息。
池化层超参数
池化窗口
池化步长
常见池化操作
最大池化
使用区域内的最大值来代表这个区域。
类似于非最大化抑制操作,保留原图中对卷积核响应比较高的地方,其他地方舍弃。
平均池化
采用区域内所有值的均值作为代表。
池化操作示例
全连接层
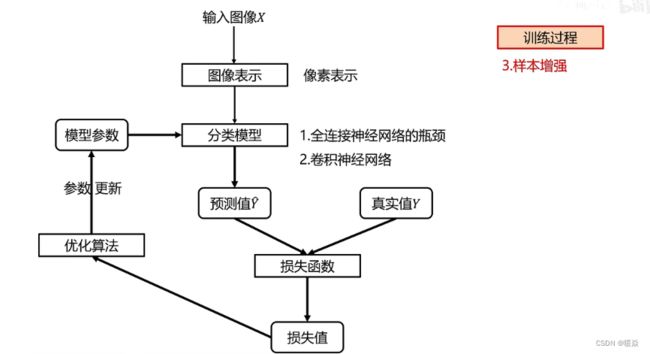
样本增强
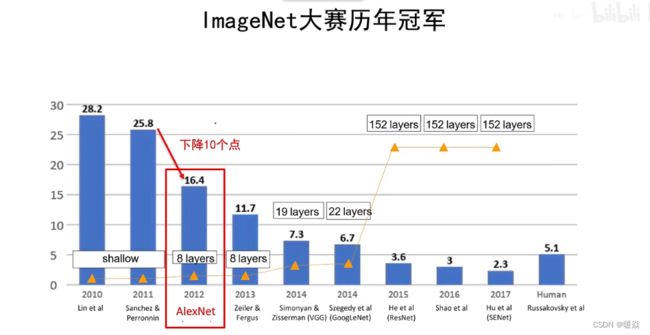
ImageNet & ILSVRC
经典网络解析
LeNet5
论文原文:Gradient-Based Learning Applied to Document Recognition
参考:网络解析(一):LeNet-5详解 – Jack Cui
参考:这可能是神经网络 LeNet-5 最详细的解释了!- 红色石头Will
LeNet-5出自论文Gradient-Based Learning Applied to Document Recognition,是一种用于手写体字符识别的非常高效的卷积神经网络。
LeNet5 这个网络虽然很小,但是它包含了深度学习的基本模块:卷积层,池化层,全链接层。是其他深度学习模型的基础。
LeNet-5共有7层,不包含输入,每层都包含可训练参数;每个层有多个Feature Map,每个FeatureMap通过一种卷积滤波器提取输入的一种特征,然后每个FeatureMap有多个神经元。
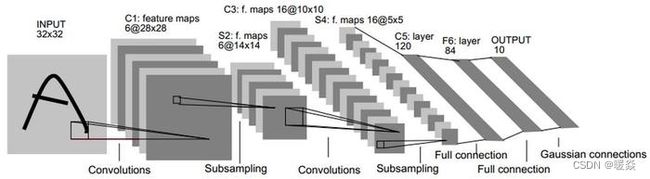
LeNet-5 与现在通用的卷积神经网络在某些细节结构上还是有差异的,例如 LeNet-5 采用的激活函数是 sigmoid,而目前图像一般用 tanh,relu,leakly relu 较多;LeNet-5 池化层处理与现在也不同;多分类最后的输出层一般用 softmax,与 LeNet-5 不太相同。
LeNet-5 是一种用于手写体字符识别的非常高效的卷积神经网络。CNN 能够得出原始图像的有效表征,这使得 CNN 能够直接从原始像素中,经过极少的预处理,识别视觉上面的规律。然而,由于当时缺乏大规模训练数据,计算机的计算能力也跟不上,LeNet-5 对于复杂问题的处理结果并不理想。
AlexNet
参考
论文原文:ImageNet Classification with Deep Convolutional Neural Networks
AlexNet概述 - 宋希堂的文章 - 知乎
参考:深入理解AlexNet网络 - PiggyGaGa
AlexNet 中的 LRN(Local Response Normalization) 是什么 - 懒丢丢的文章 - 知乎
代码
class AlexNet(nn.Module):
"""
Neural network model consisting of layers propsed by AlexNet paper.
"""
def __init__(self, num_classes=1000):
"""
Define and allocate layers for this neural net.
Args:
num_classes (int): number of classes to predict with this model
"""
super().__init__()
# input size should be : (b x 3 x 227 x 227)
# The image in the original paper states that width and height are 224 pixels, but
# the dimensions after first convolution layer do not lead to 55 x 55.
self.net = nn.Sequential(
nn.Conv2d(in_channels=3, out_channels=96, kernel_size=11, stride=4), # (b x 96 x 55 x 55)
nn.ReLU(),
nn.LocalResponseNorm(size=5, alpha=0.0001, beta=0.75, k=2), # section 3.3
nn.MaxPool2d(kernel_size=3, stride=2), # (b x 96 x 27 x 27)
nn.Conv2d(96, 256, 5, padding=2), # (b x 256 x 27 x 27)
nn.ReLU(),
nn.LocalResponseNorm(size=5, alpha=0.0001, beta=0.75, k=2),
nn.MaxPool2d(kernel_size=3, stride=2), # (b x 256 x 13 x 13)
nn.Conv2d(256, 384, 3, padding=1), # (b x 384 x 13 x 13)
nn.ReLU(),
nn.Conv2d(384, 384, 3, padding=1), # (b x 384 x 13 x 13)
nn.ReLU(),
nn.Conv2d(384, 256, 3, padding=1), # (b x 256 x 13 x 13)
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2), # (b x 256 x 6 x 6)
)
# classifier is just a name for linear layers
self.classifier = nn.Sequential(
nn.Dropout(p=0.5, inplace=True),
nn.Linear(in_features=(256 * 6 * 6), out_features=4096),
nn.ReLU(),
nn.Dropout(p=0.5, inplace=True),
nn.Linear(in_features=4096, out_features=4096),
nn.ReLU(),
nn.Linear(in_features=4096, out_features=num_classes),
)
def forward(self, x):
"""
Pass the input through the net.
Args:
x (Tensor): input tensor
Returns:
output (Tensor): output tensor
"""
x = self.net(x)
x = x.view(-1, 256 * 6 * 6) # reduce the dimensions for linear layer input
return self.classifier(x)
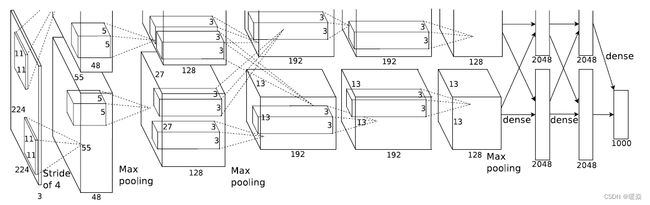
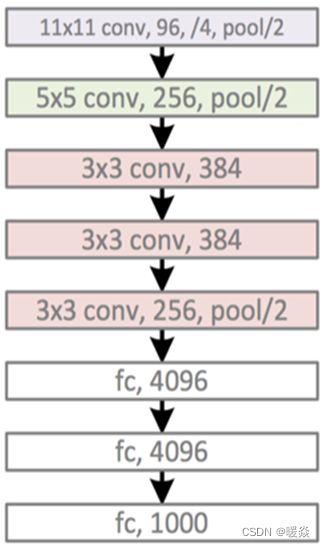
AlexNet模型结构
AlexNet运作流程
conv1:输入→卷积→ReLU→局部响应归一化→重叠最大池化层
conv2:卷积→ReLU→局部响应归一化→重叠最大池化层
conv3:卷积→ReLU
conv4:卷积→ReLU
conv5:卷积→ReLU→重叠最大池化层(经过这层之后还要进行flatten展平操作)
FC1:全连接→ReLU→Dropout
FC2:全连接→ReLU→Dropout
FC3(可看作softmax层):全连接→ReLU→Softmax
————————————————
版权声明:本文为CSDN博主「秋天的风儿」的原创文章,遵循CC 4.0
BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_40635082/article/details/123015690
AlexNet中使用的是ReLU激活函数,它5层卷积层除了第一层卷积核为1111、第二次为55之外,其余三层均为3*3,下面就详细介绍一下AlexNet的模型结构,
第一层:卷积层
卷积核大小11*11,输入通道数根据输入图像而定,输出通道数为96,步长为4。
池化层窗口大小为3*3,步长为2。
第二层:卷积层
卷积核大小5*5,输入通道数为96,输出通道数为256,步长为2。
池化层窗口大小为3*3,步长为2。
第三层:卷积层
卷积核大小3*3,输入通道数为256,输出通道数为384,步长为1。
第四层:卷积层
卷积核大小3*3,输入通道数为384,输出通道数为384,步长为1。
第五层:卷积层
卷积核大小3*3,输入通道数为384,输出通道数为256,步长为1。
池化层窗口大小为3*3,步长为2。
第六层:全连接层
输入大小为上一层的输出,输出大小为4096。
Dropout概率为0.5。
第七层:全连接层
输入大小为4096,输出大小为4096。
Dropout概率为0.5。
第八层:全连接层
输入大小为4096,输出大小为分类数。
注意:需要注意一点,5个卷积层中前2个卷积层后面都会紧跟一个池化层,而第3、4层卷积层后面没有池化层,而是连续3、4、5层三个卷积层后才加入一个池化层。
【动手学计算机视觉】第十六讲:卷积神经网络之AlexNet - Jackpop的文章 - 知乎
注:Relu之后应该是先Norm再max pooling
第一层 卷积层1
输入
输入为 224 × 224 × 3 224 \times 224 \times 3 224×224×3的图像,输入之前进行了去均值处理(AlexNet对数据集中所有图像向量求均值,均值为 224 × 224 × 3 224 \times 224 \times 3 224×224×3,去均值操作为原图像减去均值,绝对数值对分类没有意义,去均值之后的相对数值可以正确分类且计算量小)。
卷积
卷积核的数量为96,论文中两片GPU分别计算48个核;
卷积核的大小为 11 × 11 × 3 , s t r i d e = 4 11 \times 11 \times 3, stride = 4 11×11×3,stride=4, stride表示的是步长, pad = 0, 表示不扩充边缘;
卷积后的图形大小:
w i d e = ( 224 − k e r n e l _ s i z e + 2 × p a d d i n g ) / s t r i d e + 1 = 54 wide = (224 - kernel\_size + 2 \times padding) / stride + 1 = 54 wide=(224−kernel_size+2×padding)/stride+1=54
h e i g h t = ( 224 − k e r n e l _ s i z e + 2 × p a d d i n g ) / s t r i d e + 1 = 54 height = (224 - kernel\_size + 2 \times padding) / stride + 1 = 54 height=(224−kernel_size+2×padding)/stride+1=54
d i m e n t i o n = 96 dimention = 96 dimention=96
参数个数: ( 11 × 11 × 3 + 1 ) × 96 = 35 k (11 \times 11 \times 3 + 1) \times 96 =35k (11×11×3+1)×96=35k

局部响应归一化层(Local Response Normalized)
为什么要引入LRN层?
首先要引入一个神经生物学的概念:侧抑制(lateral inhibitio),即指被激活的神经元抑制相邻的神经元。归一化(normaliazation)的目的就是“抑制”,LRN就是借鉴这种侧抑制来实现局部抑制,尤其是我们使用RELU的时候,这种“侧抑制”很有效 ,因而在alexnet里使用有较好的效果。
归一化有什么好处?
1 归一化有助于快速收敛;
2 对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。
【补充:神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度,这也正是为什么我们需要对数据都要做一个归一化预处理的原因。
深度网络的训练是复杂的过程,只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。】
池化
池化pool_size = (3, 3), stride = 2, pad = 0

注:窗口大小3*3,步长2,池化过程出现重叠,现在一般不使用重叠池化。
池化结果:27x27x96 特征图组
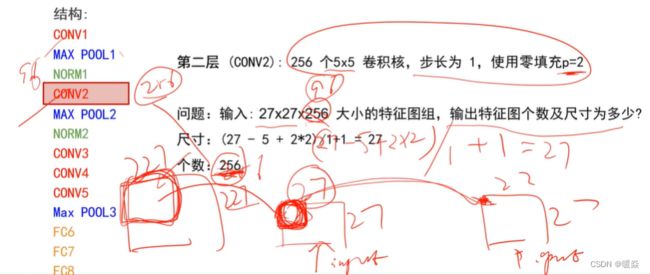
第二层 卷积层2
输入为上一层卷积的feature map,27 × 27 × 96大小的特征图组。
卷积核的个数为256个,论文中的两个GPU分别有128个卷积核。
卷积核的大小为: 5 × 5 × 48 ; p a d = 2 , s t r i d e = 1 5 \times 5 \times 48; pad = 2, stride = 1 5×5×48;pad=2,stride=1。
卷积结果:(27-5+2*2)/1+1=27,27 × 27 × 256的特征图组。
然后做LRN。
最后max_pooling, pool_size = (3, 3), stride = 2;
池化结果为:13x13x256的特征图组。
第三层 卷积层
输入为第二层的输出,卷积核个数为384,kernel_size = (3×3),padding = 1,没有LRN和Pool
输出:13×13×384,(13-3+2)/1+1
第四层 卷积层
输入为第三层的输出,卷积核个数为384,kernel_size = (3×3),padding = 1,没有LRN和Pool
输出:13×13×384,(13-3+2)/1+1
第五层 卷积层
输入为第四层的输出。
卷积核个数为256,kernel_size = (3×3),padding = 1。
卷积结果为:13×13×256,(13-3+2)/1+1
然后直接进行max_pooling, pool_size = (3, 3), stride = 2;
池化结果为:6×6×256,(13-3)/2+1=6
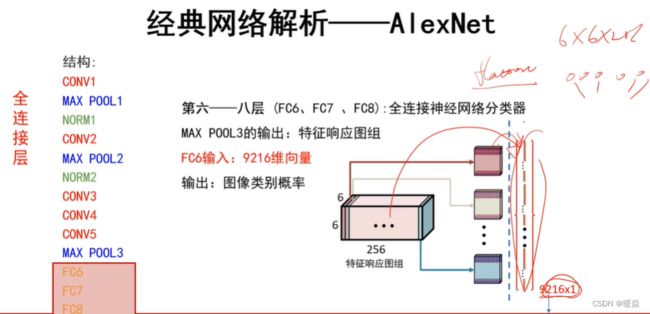
第六层&第七层&第八层 全连接层
输入:需要将第五层池化结果6×6×256转换为向量9216×1。因为全连接层不能输入矩阵,要输入向量。
重要说明
重要技巧
现在显存基本都够用,不需要再考虑分两个GPU计算。
AlexNet卷积层在做什么?
ZFNet
结构与AlexNet网络结构基本一致,加了一些改进。
参考
论文原文:Visualizing and Understanding Convolutional Networks
参考:ZFNet 详细解读 - 黑暗星球
主要改进
改进一:减小第一层卷积核
如果第一层的卷积核很大,那么第一层提取的就是粗粒度的信息,之后的层也将会丢掉细粒度的信息。相比AlexNet第一层卷积核大小为 11×11,ZFNet将第一个卷积层的卷积核大小改为7 × 7,卷积核减小,可以观察更细粒度的东西。
改进二:减小第一层卷积步长
相比AlexNet第一层的卷积步长4,ZFNet将第一层的卷积步长设置为2,为了不让原始图像的分辨率不会降低过快,不会使得图像分辨率降低过快导致信息损失的太快。
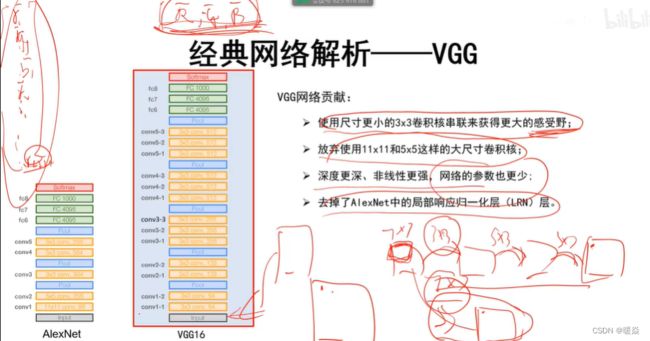
VGG16
VGG贡献
证明了增加深度,神经网络性能更好。
小卷积核串联可以获得与大卷积核相同的感受野。
AlexNet中的局部响应归一化作用不明显。
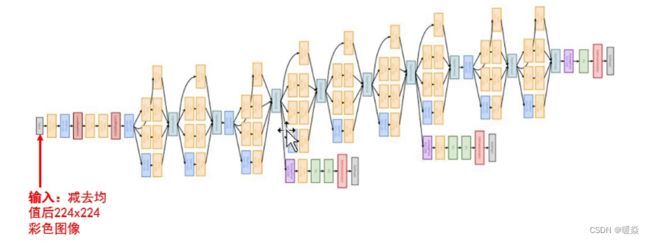
网络结构
1、输入224x224x3的图片,经64个3x3的卷积核作两次卷积+ReLU,卷积后的尺寸变为224x224x64
2、作max pooling(最大化池化),池化单元尺寸为2x2(效果为图像尺寸减半),池化后的尺寸变为112x112x64
3、经128个3x3的卷积核作两次卷积+ReLU,尺寸变为112x112x128
4、作2x2的max pooling池化,尺寸变为56x56x128
5、经256个3x3的卷积核作三次卷积+ReLU,尺寸变为56x56x256
6、作2x2的max pooling池化,尺寸变为28x28x256
7、经512个3x3的卷积核作三次卷积+ReLU,尺寸变为28x28x512
8、作2x2的max pooling池化,尺寸变为14x14x512
9、经512个3x3的卷积核作三次卷积+ReLU,尺寸变为14x14x512
10、作2x2的max pooling池化,尺寸变为7x7x512
11、与两层1x1x4096,一层1x1x1000进行全连接+ReLU(共三层)
12、通过softmax输出1000个预测结果作者:Glenn_ 链接:https://www.jianshu.com/p/1b37890989a9 来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
主要改进
输入去均值
AlexNet和ZFNet的输入去均值:求所有图像向量的均值,最后得出一个与原始图像大小相同维度的均值向量。
VGG输入去均值:求所有图像向量的RGB均值,最后得到的是一个3×1的向量 [R,G,B]
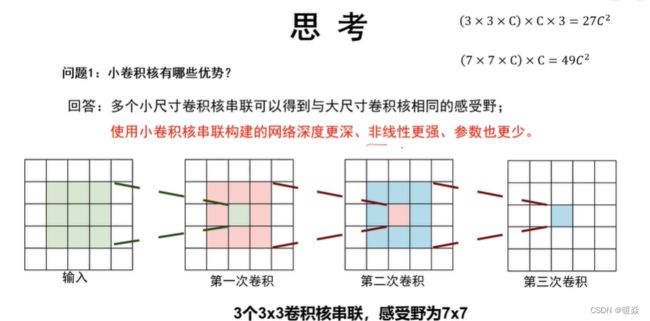
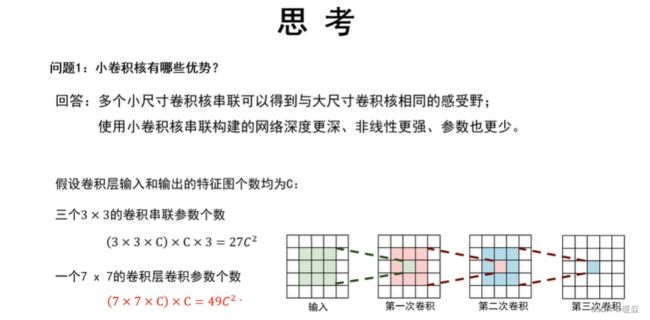
小卷积核串联代替大卷积核
增加了非线性能力。
多个小尺寸卷积核串联可以得到与大尺寸卷积核相同的感受野。
与高斯核不同,高斯核中两个小卷积核组合卷积核大卷积核卷积结果相同。但是卷积神经网络中的卷积核,多个小卷积核组合和大卷积核结果不同,但是感受野相同。
无重叠池化
窗口大小为2×2,步长为2。
卷积核个数逐层增加
前层卷积核少,是因为前层学习到的是图像的基元(点、线、边),基元很少,所以不需要很多的神经元学习,又前层的图像都比较大,若神经元很多,计算量会很大(K×m×m×D×K×n×n)。到后面的层时,包含很多的语义结构,需要更多的卷积核学习。


全连接第一个隐层的参数个数:7×7× 512× 4096 = 102,760,448,卷积核个数增加到512就不能再增加。
GoogLeNet
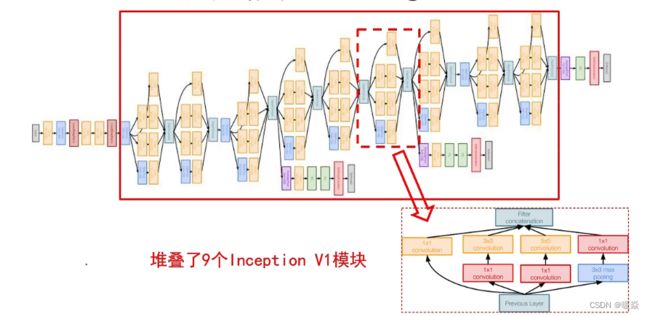
GoogLeNet模型结构
对上图做如下说明:
1 . 显然GoogLeNet采用了模块化的结构,方便增添和修改;
2 . 网络最后采用了average pooling来代替全连接层,想法来自NIN,事实证明可以将TOP1 accuracy提高0.6%。但是,实际在最后还是加了一个全连接层,主要是为了方便以后大家finetune;
3 . 虽然移除了全连接,但是网络中依然使用了Dropout ;
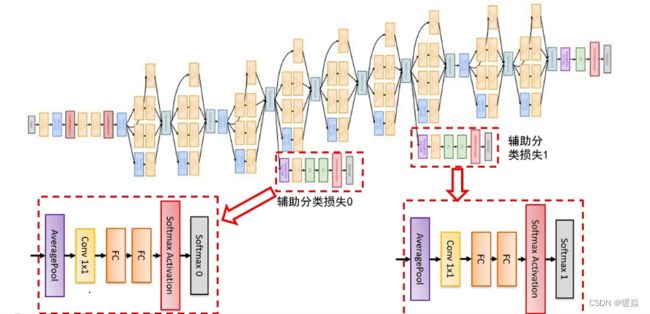
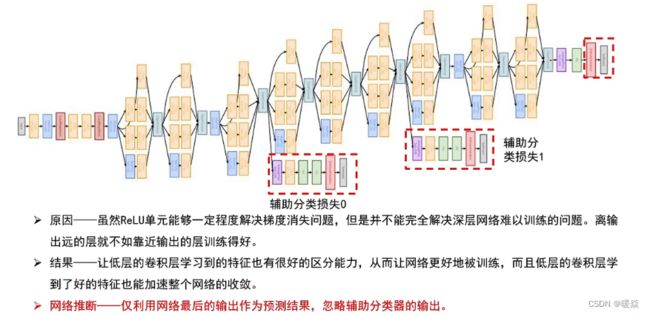
4 . 为了避免梯度消失,网络额外增加了2个辅助的softmax用于向前传导梯度。文章中说这两个辅助的分类器的loss应该加一个衰减系数,但看caffe中的model也没有加任何衰减。此外,实际测试的时候,这两个额外的softmax会被去掉。
参考:GoogLeNet系列解读 - shuzfan
数据预处理
零均值化(zero-mean) 中心化,即使像素值范围变为[-128,127],以0为中心。
这样做的优点是为了在反向传播中加快网络中每一层权重参数的收敛。
创新点
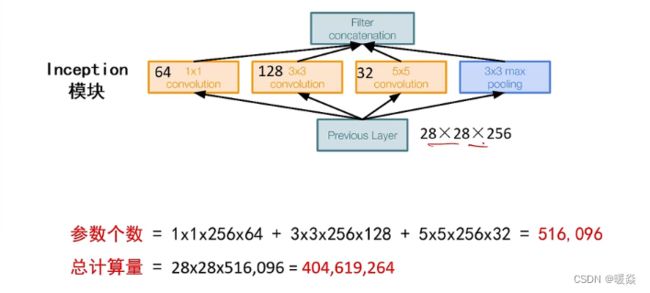
Inception结构
Inception 结构的主要思路是怎样用密集成分来近似最优的局部稀疏结构。
作者首先提出下图这样的基本结构:
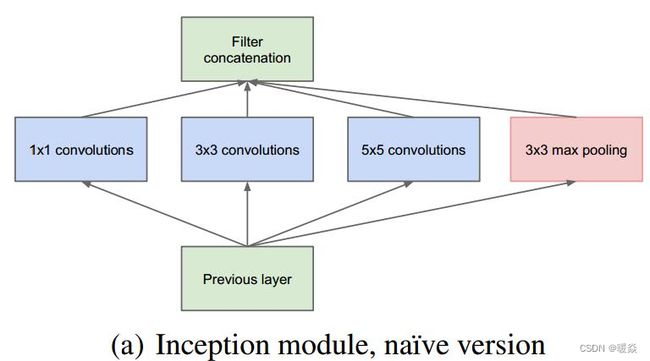
对上图做以下说明:
1 . 采用不同大小的卷积核意味着不同大小的感受野,最后拼接意味着不同尺度特征的融合;
2 . 之所以卷积核大小采用1、3和5,主要是为了方便对齐。设定卷积步长stride=1之后,只要分别设定pad=0、1、2,那么卷积之后便可以得到相同维度的特征。
3 . 3×3 max pooling 可理解为非最大化抑制。文章说很多地方都表明pooling挺有效,所以Inception里面也嵌入了。保留且加强了原图中比较重要的信息。
4 . 网络越到后面,特征越抽象,而且每个特征所涉及的感受野也更大了,因此随着层数的增加,3x3和5x5卷积的比例也要增加。
5 . 1×1 3×3 5×5卷积,及3×3max pooling,通过设定合适的pad都会得到相同维度的特征,然后将这些特征直接拼接在一起。
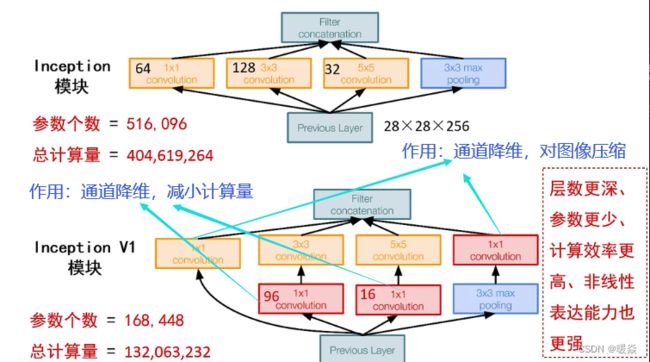
但是,使用5x5的卷积核仍然会带来巨大的计算量。 为此,文章借鉴NIN2,采用1x1卷积核来进行降维。
例如:上一层的输出为100x100x128,经过具有256个输出的5x5卷积层之后(stride=1,pad=2),输出数据为100x100x256。其中,卷积层的参数为128x5x5x256。假如上一层输出先经过具有32个输出的1x1卷积层,再经过具有256个输出的5x5卷积层,那么最终的输出数据仍为100x100x256,但卷积参数量已经减少为128x1x1x32 + 32x5x5x256,大约减少了4倍。
平均池化+去除两个全连接层
辅助分类器
思考
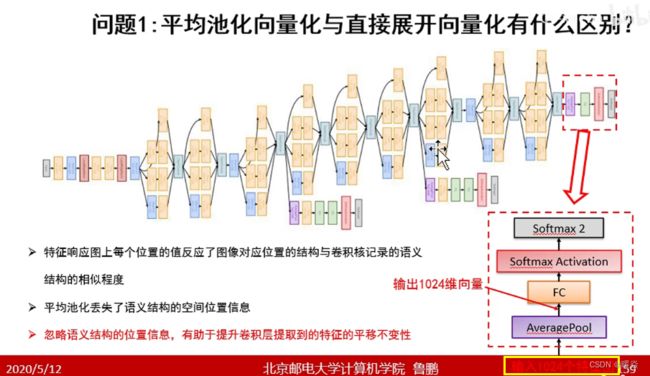
问题1 :平均池化向量化与直接展开向量化有什么区别?
特征响应图中位置信息不太重要,平均池化,忽略位置信息,可以很大节省计算量。
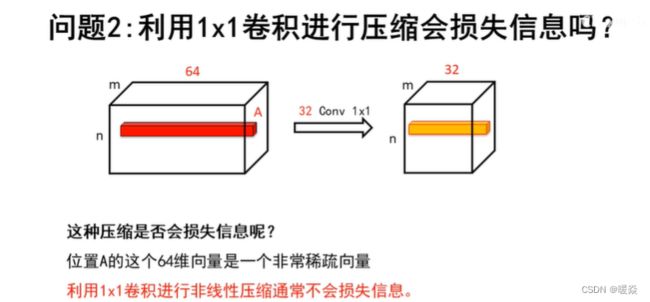
问题2: 利用1 x1卷积进行压缩会损失信息吗?
不会,假设图像或特征响应图深度通道为64,其中记录信息的只有少数,对应的向量非常稀疏,且其后的每个卷积核(深度通道也为64)都作用在这64个通道上。 经过压缩,并不会影响图像原始信息的记录。
ResNet
ResNet论文:Deep Residual Learning for Image Recognition
Resnet之后的网络应用在ImageNet之外的问题上,效果不一定好。

产生背景
贡献
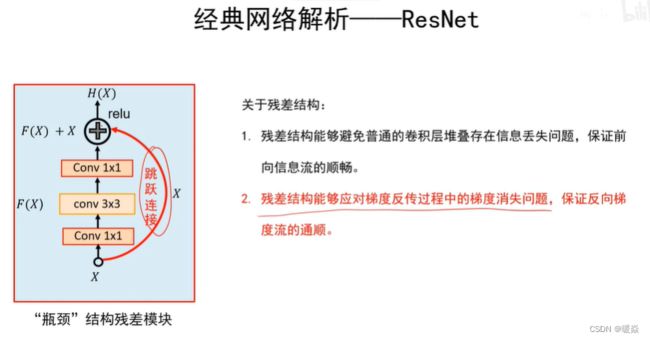
残差模块
前向传递:原始信息一直被保存的很好,没有丢失信息,信号不容易衰减,前向信息流就很顺畅。
X之后的1×1卷积核:降维,减少3×3卷积的运算量。
3×3之后的1×1卷积核:升维(还原X的维度),为了实现X+F(X)。
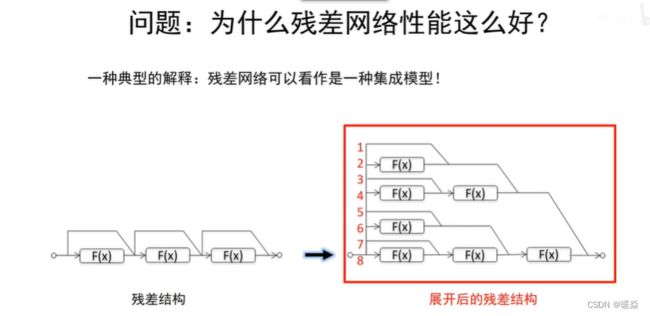
为什么残差网络性能好?
残差网络为何有效,都有哪些发展? - 十三的回答 - 知乎