【力扣周赛】第 363 场周赛（完全平方数和质因数分解）

竞赛链接

https://leetcode.cn/contest/weekly-contest-363/

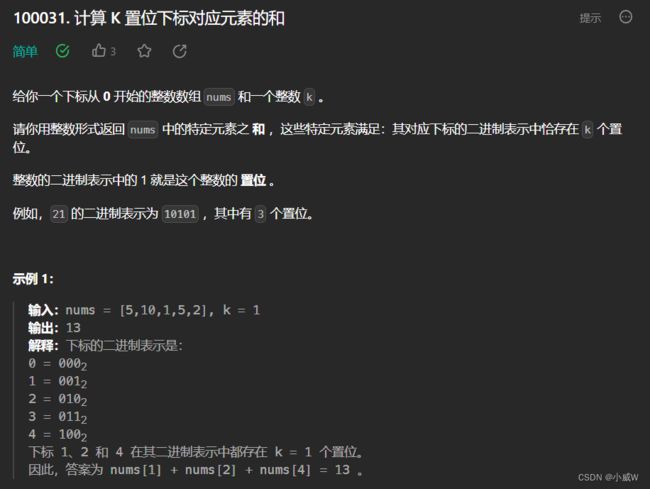
Q1：100031. 计算 K 置位下标对应元素的和

https://leetcode.cn/problems/sum-of-values-at-indices-with-k-set-bits/

提示：
1 <= nums.length <= 1000
1 <= nums[i] <= 10^5
0 <= k <= 10

竞赛时代码

class Solution {
    public int sumIndicesWithKSetBits(List<Integer> nums, int k) {
        int ans = 0;
        for (int i = 0; i < nums.size(); ++i) {
            if (Integer.bitCount(i) == k) ans += nums.get(i);
        }
        return ans;
    }
}

写法2——手写二进制中1的数量

class Solution {
    public int sumIndicesWithKSetBits(List<Integer> nums, int k) {
        int ans = 0;
        for (int i = 0; i < nums.size(); ++i) {
            if (cnt(i) == k) ans += nums.get(i);
        }
        return ans;
    }

    public int cnt(int x) {
        int res = 0;
        while (x != 0) {
            res++;
            x &= x - 1;
        }
        return res;
    }
}

Q2：100040. 让所有学生保持开心的分组方法数（排序后枚举分界）

https://leetcode.cn/problems/happy-students/description/

提示：
1 <= nums.length <= 10^5
0 <= nums[i] < nums.length

竞赛时代码

将学生排序后， 一个学生 x 被选了的时候，比它小的一定必须被选；同理一个学生 y 不被选的时候，比它大的一定不能被选。

枚举每个位置，假设 0~i 被选择，i+1~n-1 不被选择。检查是否合理，合理则 ans ++；

class Solution {
    public int countWays(List<Integer> nums) {
        // 按题意——一定先选择nums值更小的学生，所以——从小到大排序
        Collections.sort(nums);
        int n = nums.size(), ans = 0;
        if (nums.get(0) > 0) ans++;     // 处理特例是否可以全不选
        // 枚举选择到每个位置
        for (int i = 0; i < n; ++i) {  
            // 检查已经选择人数i+1是否严格大于nums[i]
            if (i + 1 > nums.get(i)) { 
                // 检查已经选择人数i+1是否严格小于下一个没被选择的学生nums[i+1]  （注意要判断越界）
                if (i + 1 < n && nums.get(i + 1) <= i + 1) continue;    // 不满足就跳过
                ans++;  // 这个位置合理，答案+1
            }
        }
        return ans;
    }
}

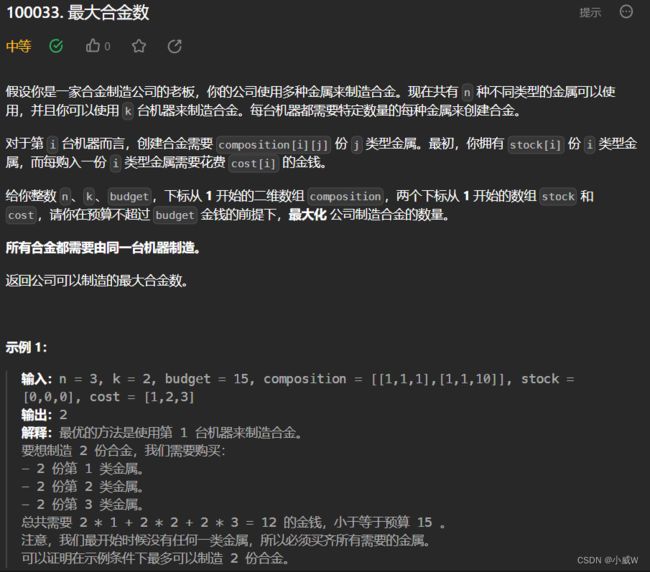
Q3：100033. 最大合金数（二分答案）

https://leetcode.cn/problems/maximum-number-of-alloys/description/

提示：
1 <= n, k <= 100
0 <= budget <= 10^8
composition.length == k
composition[i].length == n
1 <= composition[i][j] <= 100
stock.length == cost.length == n
0 <= stock[i] <= 10^8
1 <= cost[i] <= 100

竞赛时代码

注意到题目中说明——“所有合金都需要由同一台机器制造。”，且观察到 k 的数据范围较小，所以可以枚举使用每台机器。
对于每台机器，使用二分查找求出它可以制造出的最大的合金数量。

二分查找时判断的依据是花费的前有没有在 budget 的范围内。

class Solution {
    public int maxNumberOfAlloys(int n, int k, int budget, List<List<Integer>> composition, List<Integer> stock, List<Integer> cost) {
        long ans = 0;
        // 按照题意，所有合金都需要由同一台机器制造。枚举每个机器。
        for (int i = 0; i < k; ++i) {
            ans = Math.max(ans, op(n, budget, composition.get(i), stock, cost));
        }
        return (int)ans;
    }
    
    // 计算使用某台机器时的最大制造数量
    public long op(int n, int budget, List<Integer> composition, List<Integer> stock, List<Integer> cost) {
        // 二分答案
        long l = 0, r = (long)Integer.MAX_VALUE;
        while (l < r) {
            long mid = l + r + 1 >> 1;
            if (check(mid, n, budget, composition, stock, cost)) l = mid;
            else r = mid - 1;
        }
        return l;
    }
    
    // 检查是否可以造出 k 个合金
    public boolean check(long k, int n, int budget, List<Integer> composition, List<Integer> stock, List<Integer> cost) {
        long s = 0;     // 记录额外花费
        for (int i = 0; i < n; ++i) {
            long need = k * composition.get(i);
            if (need <= stock.get(i)) continue;
            s += cost.get(i) * (need - stock.get(i));
            if (s > budget) return false;   // 额外花费超了，不能造出k个合金
        }
        return true;
    }
}

Q4：8041. 完全子集的最大元素和

https://leetcode.cn/problems/maximum-element-sum-of-a-complete-subset-of-indices/description/

提示：
1 <= n == nums.length <= 10^4
1 <= nums[i] <= 10^9

竞赛时代码——质因数分解+哈希表

对每个下标质因数分解，两两相乘之后的结果是完全平方数，那么这两个数字的质因数分解的奇偶性相同。 例如2=2^1，8=23；相同质因数出现的次数的奇偶性相同，则两者可以匹配。

根据质因数分解的结果将所有数字分组即可。

class Solution {
    public long maximumSum(List<Integer> nums) {
        // 两两之间相乘之后是完全平方数，则质因数分解结果满足各个质因数数量奇偶性相同
        int n = nums.size();
        String[] mask = new String[n];
        long ans = 0;
        // key是mask,value是sum
        Map<String, Long> m = new HashMap<>();     
        for (int i = 1; i <= n; ++i) {
            mask[i - 1] = op(i);                                        // 计算mask
            m.merge(mask[i - 1], (long)nums.get(i - 1), Long::sum);     // 求和
            ans = Math.max(ans, m.get(mask[i - 1]));                    // 更新答案
        }
        return ans;
    }
    
    // 计算下标x的质因数分解掩码mask
    public String op(int x) {
        // 将质因数的数量为奇数的部分记录下来
        String mask = "";
        for (int i = 2; i <= x / i; ++i) {
            if (x % i == 0) {
                int s = 0;
                while (x % i == 0) {
                    s++;
                    x /= i;
                }
                if (s % 2 == 1) mask += String.valueOf(i) + " ";
            }
        }
        if (x > 1) mask += String.valueOf(x) + " ";
        return mask;
    }
}

解法2——定义core(x)为 x 除去完全平方因子后的剩余结果

https://leetcode.cn/problems/maximum-element-sum-of-a-complete-subset-of-indices/solutions/2446037/an-zhao-corei-fen-zu-pythonjavacgo-by-en-i6nu/

计算方式同质因数分解，把 n 的所有出现次数为奇数的质因子相乘，即为 core(n)。

class Solution {
    public long maximumSum(List<Integer> nums) {
        // 两两之间相乘之后是完全平方数，则质因数分解结果满足各个质因数数量奇偶性相同
        int n = nums.size();
        long[] sum = new long[n + 1];
        long ans = 0;
 
        for (int i = 1; i <= n; ++i) {
            int c = op(i);                 // 计算mask
            sum[c] += nums.get(i - 1);     // 求和
            ans = Math.max(ans, sum[c]);   // 更新答案
        }
        return ans;
    }
    
    // 计算下标x的质因数分解掩码mask
    public int op(int x) {
        // 将质因数的数量为奇数的部分记录下来
        int res = 1;
        for (int i = 2; i <= x / i; ++i) {
            if (x % i == 0) {
                int s = 0;
                while (x % i == 0) {
                    s++;
                    x /= i;
                }
                if (s % 2 == 1) res *= i;
            }
        }
        if (x > 1) res *= x;
        return res;
    }
}

成绩记录

T4 没有那么难！想得慢了！