论文阅读：EasyMesh: An efficient method to reconstruct 3D mesh from a single image

Abstract

本文提出了一种有效解决此问题的新方法，通过使用专门设计的 GAN 模型将给定的自然图像映射到几何图像，从中可以重建相应的 3D 网格。具体来说，是将视点估计（viewpoint estimation）和 3D 重建任务分开，确保重建网络专注于生成具有准确视点信息的生动 3D 网格。
作者还添加了一个可微分模块来为合成的几何图像从不同的视角创建轮廓（add a differentiable module to create silhouettes from various viewpoints for the synthesized geometry image），旨在提高生成的 3D 模型与其输入的 2D 图像之间的一致性。
此外，作者为几何图像设计了一个紧凑但有效的鉴别器，以保证生成对象的整体轮廓合理。

Introduction

关于点云（point clouds）点云
从单个自然图像重建完整的 3D 模型现在仍然是一个具有挑战性和持续性的问题。
传统的 3D 形状重建方法通常基于预定义的模板，并通过从源数据库中检索和组装相似的零件或对象来生成 3D 模型（Chaudhuri 等人，2011 年；Kalogerakis 等人，2012 年）。尽管生成的 3D 模型质量很高，但这种方法仅限于重新组合现有部件，无法合成他们从未见过的新对象。

基于深度学习的方法可以对新型 3D 形状的不确定性进行建模。大多数基于深度神经网络的现有作品都将Voxels (三维像素)作为 3D 形状的表示，并采用体积卷积网络（volumetric convolutional networks）进行形状合成（Girdhar 等，2016；Wu 等，2016；Yan 等，2016）。

然而，由于额外的维度，体积卷积操作比二维卷积占用更多的内存，这限制了体积分辨率的扩展。此外，体积表示是信息稀疏的。体积卷积花费昂贵的计算资源来处理表面内无用的信息是低效的。一些研究人员试图避免体积表示并从多个视点渲染深度图像（avoid volumetric representation and render depth images from multiple viewpoints）（Soltani 等人，2017 年；Lin 等人，2017 年）。尽管这些方法通常很有效，但从预测的深度图像重建的 3D 形状很容易在空间周围散布噪声点。
这主要是由于视点估计和深度图像渲染的纠缠过程造成的（This is mainly caused by the entangled process of viewpoint estimation and depth image rendering）。
在没有用于监督的视点信息的情况下，很难从其他训练资源中精确地预测给定视点上的深度图像。
也存在一些直接处理点云（point clouds）的生成方法。

然而，这些方法生成的 3D 形状（Fan et al., 2017）通常在表面上缺乏平滑度，这使得很难转换为网格。最近提出的 Pixel2Mesh（Wang et al., 2018）采用复杂的图形网络从单个图像中恢复 3D 网格。
Pixel2Mesh++ (Wen et al., 2019) 进一步结合了来自多个视图的信息，并使用图形卷积网络稍微调整了点云的坐标。尽管具有生成高质量网格的能力，但它需要预先定义点和边之间的关系，这使得它不太灵活。此外，训练需要自然图像的配对数据及其相应的 3D 形状，这使得构建具有满意样本的大型存储库变得非常重要。

在本文中，作者提出了一种从单个自然图像重建 3D 网格的两阶段方法。在第一阶段对对象的轮廓进行分割，并将其馈送到第二阶段的网格重建网络。两个阶段的分离训练过程不再需要配对的 3D 对象和自然图像。
这两个数据集都很容易获取，作者认为这有利于每个阶段的训练过程，同时不会降低泛化能力。
作者考虑另一种表示，几何图像（Gu 等人，2002 年；Sinha 等人，2016 年），用于 3D 网格生成。
给定一个 3D 对象，相应的几何图像对表面上采样的点的坐标进行编码（the corresponding geometry image encodes the coordinates of points sampled on the surface)，这本质上是一种类似图像格式的点云的特殊排列。
通过这种方式，可以将2D 卷积操作应用于几何图像，避免体积卷积或复杂图卷积的昂贵计算成本。

作者结合了视点估计和轮廓重新渲染模块（incorporate the viewpoint estimation and silhouette re-rendering modules），使生成的 3D 形状与输入图像重合。此外，在表面上定义了几个新的损失，以确保生成的网格模型的平滑性和连续性。

与其他最先进的 3D 重建方法相比，定性和定量评估都证明了此方法的优越性。

本文的主要贡献有三方面：

首先，提出了一种新颖的两阶段方法来从单个自然图像重建 3D 网格。
其次，设计了一个高效的 3D 形状特征提取器作为鉴别器。
第三，结合视点估计和轮廓渲染模块来强制生成的 3D 形状和输入图像之间的一致性

Related work

3D 视觉中的生成对抗网络。

对于 3D 形状生成问题，很少有方法引入鉴别器。
3D-GAN（Wu et al., 2016）是第一个采用 GAN 架构并将低维噪声向量映射到 3D 模型空间的方法。
PrGAN(Gadelha et al., 2017) 添加了一个额外的投影仪来从生成的 3D 体积渲染 2D 图像，它的鉴别器将生成的图像与真实图像区分开来。

朱等人。 (2018) 训练了一个由图像增强器、3D 模型生成器和两个分别对图像和 3D 模型进行操作的鉴别器组成的两分支模型。上述方法合成 3D 体积，不能表示准确的几何体。
其他格式，例如网格，很难被神经网络处理，因为表面很难表示和输入网络。

本文利用在几何图像上操作的 2D 卷积，它有效地编码点的坐标并以类似图像的格式排列点云。此外，3D 形状特征提取器专为几何图像而设计，可作为鉴别器来增强 3D 形状细节。（we leverage 2D convolutions operated on the geometry image, which efficiently encode coordinates of points and arrange the point cloud in an image-like format. Furthermore, a 3D shape feature extractor is specifically designed for geometry images and serves as the discriminator to enhance 3D shape details.）

3D shape reconstruction

尽管基于多视图几何（multi-view geometry）的 3D 重建已经取得了很大的进步，例如 SLAM（Fuentes-Pacheco 等，2015），但研究人员对从单个图像生成 3D 形状越来越感兴趣。
由于遮挡，单个图像显然无法覆盖 3D 对象的整个形状信息。
基于深度学习的方法模拟 3D 存储库的数据分布，并显示出强大的建模不确定性和预测对象不可见部分的能力。

一些先驱作品（Choy 等人，2016 年；Girdhar 等人，2016 年）将底层 3D 对象预测为 3D 体积(predicted the underlying 3D object as 3D volume)，通常仅限于 32 ×32 ×32 的低分辨率，丢弃了详细信息。后期作品探索了各种格式来表示 3D 模型。范等人(2017) 提出了一种合成点云的网络，并使用距离度量损失（即倒角距离或 EM 距离损失）来训练网络(proposed a fancy network synthesizing point clouds and trained the network with a distance metric loss)，其时间复杂度与点数的平方成正比，在训练时表现出低效率。邹等人。 (2017) 制作了许多不同比例和旋转角度的图元，并按顺序组装它们以构建结构简单的对象。也有一些工作可以预测多个给定视点的深度图像（Soltani et al., 2017; Lin et al., 2017）。尽管可以有效地训练这些方法，但预测深度图像的实际视点很难精确地聚焦在所需的视点上。
因此，当从深度图像重建点云时，经常会发生错位。

许多工作专注于生成 3D 网格模型而不是点云或体素（Groueix 等人，2018 年；Kato 等人，2018 年；Liu 等人，2019 年）。先驱工作 Pixel2Mesh(Wang et al., 2018) 直接预测点云的坐标，并利用预先定义的点和网格之间的关系重建表面。
与 Pixel2Mesh 相比，作者取得了可比的结果，具有两个优势。

一方面，我们不需要成对的 3D 形状和相应的自然图像，这简化了收集包含对齐对的大型存储库的要求。
另一方面，避免了点之间复杂邻接关系的定义，因此可以使用灵活简单的方法从预测的几何图像重建光滑表面。

Method description

作者方法的目标是通过使用深度神经网络合成的几何图像，从单个自然图像重建高质量的 3D 网格模型。
图 2 说明了模型的整体流程，它由以下两个阶段组成。

第一阶段包含一个现成的语义分割网络 Deeplab v3+（Chen et al., 2018），它能够从给定的自然图像中精确提取对象的轮廓。（就是对于每个像素的分类， logits是网络的输出，logits.shape=(batch_size, w, h, 21)，21类语义标签。）
然后，将轮廓图像输入到第二部分以生成 3D 模型。
作者没有以端到端的方式训练整个模型，即直接将自然图像转换为 3D 形状，而是分别训练这两个部分，因为我们发现很难获得包含大量 3D 模型的数据集作为它们对应的自然图像。

作者的 3D 形状重建模型的细节如下：

3D shape generator

作者的 3D 形状生成器包含一个图像编码器和一个 3D 形状转换网络，可将输入轮廓图像映射到其相应的几何图像。在介绍主干之前，先简单分析一下几何图像的属性。
几何图像包含 3 个通道（channels），分别对应点的 x、y、z 坐标。几何图像中的像素代表 3D 空间中的一个点。此外，几何图像中的相邻像素在 3D 点云中保持其相邻关系。
基于这一观察，可以应用卷积相关操作来捕捉局部形状结构。
作者的图像编码器包括 3 个通道大小为 {32, 64, 96}、内核大小为 3 ×3 的残差块和两个 3 ×3 步长为 2 的卷积操作，将分辨率为 64 ×64 的输入轮廓图像嵌入到一个紧凑的特征空间中。（Our image encoder includes 3 residual blocks with channel size {32, 64, 96}, kernel size 3 ×3 and two 3 ×3 convolutional operations with stride 2, embedding the input silhouette image whose resolution is 64 ×64into a compact feature space.）
这些编码特征包含对象的形状信息，并引导形状变换网络生成所需的 3D 形状。形状变换网络不是直接将紧凑的特征向量解码为 3D 形状，而是从小尺寸的几何图像开始。
初始几何图像大小为 16 × 16 × 3，对应于在单位球表面均匀采样的 256 个点。（The initial geometry image is of size 16 ×16 ×3and corresponds to 256 points that are uniformly sampled on the surface of a unit ball）
我们采用由粗到细的策略，通过编码器的交互引导将初始几何图像逐渐雕刻成目标形状。
形状变换网络包含两个交替操作：形状变形和点增强
在形状变形步骤中，模型结合来自图像编码器的形状信息并提取附加到每个点的特征以向目标形状变形
在点增强步骤中，我们结合对几何图像的双线性插值和反卷积操作来增加点的数量。由于几何图像的特性，上采样后新生成的点来自它们相邻的旧点，我们不需要在点之间分配连接关系。
插值后的几何图像跳跃式连接到下一个变形网络的末端，使变形网络专注于学习细微的调整以矫正 3D 形状。经过两次上采样操作，几何图像的分辨率增加到 64×64，包含 4096 个点，足以表示一个 3D 形状

作者在多个层次上施加监督，使形状转换过程更加可控。作者发现，简单地计算生成的几何图像与其相应的地面实况之间的 L2losses 可能会导致生成扭曲和平均的 3D 形状。因此，转而使用点云之间的倒角损失。

假设生成的和ground-truth的几何图像都由N个点和点xin的邻域N(x)组成，几何图像定义为一个以x为中心的K×Kgrid，原始倒角损失需要寻找最近邻源中每个点的目标，其时间复杂度为 O(N2)。在本文中，我们提出了在几何图像上操作的局部倒角损失，它只是为源中的每个点 xin 找到与目标中 N(x) 对应的区域最近的点。这种简化将时间复杂度从 O(N2) 降低到 O(NK2)。建议的局部倒角距离定义为:

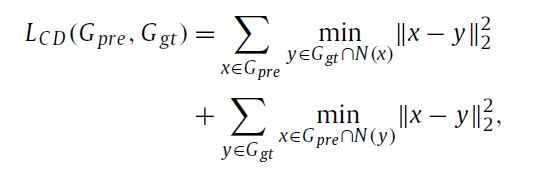
其中 Gpre 和 Ggt 分别是预测和真实几何图像。
仅在点云上施加倒角损失并不能保证光滑的表面，因此我们引入法线损失使地面实况法线位于与其切线垂直的点上

其中 ni 是点 pi 处的真实法线。在实践中，后一项可以通过在 pi 处应用深度卷积和固定核 Ktan 来有效计算

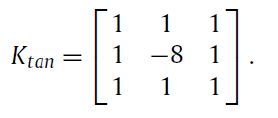
类似于王等人 (2018)，使用边长正则化来避免飞点（use the edge length regularization to avoid flying points）

然后，我们得到施加在网格上的最终损失函数

在实践中，我们发现上述损失函数在几何图像的内部区域效果很好，但对四个边缘施加的限制很少，这可能会导致严重的表面扭曲。
根据折叠规则，如图3所示，我们建议用逆对称填充来填充生成的几何图像。

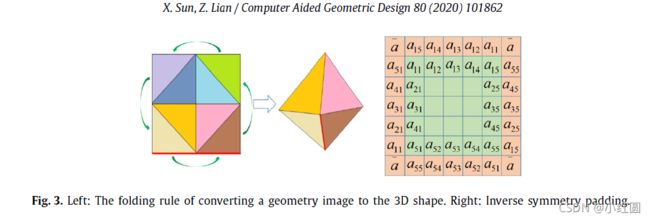
我们转置每条边中元素的顺序，并用这四个新边围绕生成的几何图像。
在计算上述损失时，仅对生成的图像进行填充，而不是对解码器的中间层进行填充，就足以消除不准确的边缘连接并避免表面失真。

3D shape discriminator

如上所述，几何图像实际上是以类似图像的格式排列的点云。因此，用于处理图像和点云的工具都可以用于处理几何图像。专门为处理点云而设计的网络，如 PointNet（Qi 等人，2017），尽管容量强大，但仍包含大量参数。作为整个网络的一部分，鉴别器需要在参数数量和表示 3D 形状特征的能力之间进行权衡。受Shen等人的启发（2018 年），处理乱序点云，我们针对有序点云调整我们的判别器。如图 4 所示，我们的鉴别器从一个动态形状感知模块开始。

我们使用各种卷积来感知多个感受野的局部 3D 形状结构。这些多尺度特征通过全局平均池化层形成 3D 形状的全局描述，然后由多层感知 (MLP) 使用来学习确定每个特征图重要性的权重。动态分配机制强调捕捉 3D 形状的有区别的局部结构的特征图。之后，将获得的特征图与原始几何图像连接起来。重构后的 (w ×h) ×(L +3) 矩阵中的每一行都对一个点的特征进行编码。全局平均池化层进一步排除了点序的影响，输出了 3D 形状的最终表示。最后，作为分类器的三个全连接层计算输入 3D 形状被识别为真实的概率。生成器和鉴别器的损失函数可以表示为

其中y表示ground-truth几何图像，s表示输入轮廓图像，G(s)表示合成几何图像，D(•)表示判别器输出的概率值

Viewpoint estimation（视点估计）

估计给定场景图像的相机姿态是很重要的。在本文中，我们专注于如何估计轮廓图像的视点（focus on how to estimate viewpoints for silhouette images)。
考虑到我们通过OpenGL渲染轮廓图像进行训练的过程，可以调整三组参数来确定渲染对象在2D图像上出现的姿势：相机在世界坐标系中的位置，相机镜头的方向面，以及相机向上矢量的方向。
在合成轮廓图像并使用从 VGG 改编的深度神经网络来回归这些参数时，我们尝试了上述三个参数的各种设置和组合。它适用于某些场景中的某些配置，但对其他人却不尽如人意。因此，我们简化了我们的视点估计模块，通过裁剪轮廓图像并将对象放置在图像的中心，切断第二个参数的预测并将相机镜头面向的方向固定在 (0, 0, 0)。此外，我们假设向上向量的方向仍然是 (0, 1, 0)，其在图像平面上的投影决定了场景坐标系的 y 轴。基于这些假设，我们可以推导出相机的旋转矩阵 R。因此，唯一需要预测的参数是相机的位置。这里，一个类似 VGG 的网络被用于预测相机的坐标 (x, y, z) 并且视点估计的损失函数被定义为:

剪影图像重新渲染 (Silhouette image re-rendering)

大多数现有的 3D 重建方法只能恢复看起来与输入 2D 图像相似的 3D 对象的粗略轮廓。
要获得高质量的 3D 对象，必须增强 3D 表面的细节。
一个直观的想法是，我们需要找到一种合适的方法来计算 3D 形状描述符，并使真实 3D 对象和合成对象的表示尽可能相似。

理想的描述符应该具有表现力和辨别力，并且计算成本低。
为了将描述符嵌入到整个流水线中并使其能够以端到端的方式进行训练，特征提取模块也应该是可微的。
基于这一见解，我们选择从 3D 点云重新渲染的多个视点的轮廓作为描述符，并设计可微分的管道来实现目标。我们推测，如果渲染的轮廓与其对应的地面实况轮廓匹配得很好，那么生成的 3D 形状应该具有良好的细节。类似的想法在之前的作品中也出现过，例如 (Tulsiani et al., 2018; Yang et al., 2018)，其中从体素数据投影的图像作为优化的主要监督。然而，在本文中，轮廓是从点云渲染的，仅起到次要作用，旨在确保与地面实况对象的一致性。给定视点 i 的旋转矩阵 Riand 变换矩阵，规范坐标系中的每个点都可以通过以下方式映射到图像坐标

其中 Ki 是相机内在矩阵，pi 是点的 3D 规范坐标，x 表示 (xc, yc, zc) 其中 (xc, yc) 是 2D 图像平面中的对应坐标，zc 表示深度值。当从点云投影到 2D 图像时，一些点是否碰撞并落在同一像素上并不重要，因为我们很少关心深度信息。轮廓可以通过下面式子

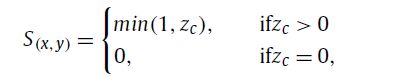
并且我们重新渲染模块中每个像素的损失函数定义为：

其中
分别是在视点 i 处从预测点云和地面实况点云渲染的轮廓，视点总数为 N。我们惩罚本应在视点内部的“空”像素对象的轮廓通过添加一个掩码M，其中如果S（x，y）=1，则权重值选择为3，如果S（x，y）=0，则选择权重值为1。最后，整体训练损失可以写为

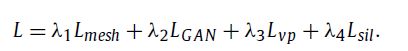
我们交替训练生成器和判别器直到收敛，然后生成器获得了 3D 形状重建的能力

从几何图像重建表面（Surface reconstruction from geometry image）

由于几何图像中相邻点之间的相邻关系，我们可以轻松地恢复 3D 网格的表面。

请注意，基于几何图像构建网格的方式并不是唯一的，这里我们采用一种简单有效的方式。

如图 5 所示，对于每个由四个相邻点组成的四边形，我们连接它的四个边和一个对角线。

通过此操作，可以获得 watertight 3D mesh。