Go-Python-Java-C-LeetCode高分解法-第六周合集
前言
本题解Go语言部分基于 LeetCode-Go
其他部分基于本人实践学习
个人题解GitHub连接:LeetCode-Go-Python-Java-C
Go-Python-Java-C-LeetCode高分解法-第一周合集
Go-Python-Java-C-LeetCode高分解法-第二周合集
Go-Python-Java-C-LeetCode高分解法-第三周合集
Go-Python-Java-C-LeetCode高分解法-第四周合集
Go-Python-Java-C-LeetCode高分解法-第五周合集
本文部分内容来自网上搜集与个人实践。如果任何信息存在错误,欢迎读者批评指正。本文仅用于学习交流,不用作任何商业用途。
欢迎订阅专栏,每日一题,和博主一起进步
LeetCode专栏
36. Valid Sudoku
题目
Determine if a 9x9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:
- Each row must contain the digits
1-9without repetition. - Each column must contain the digits
1-9without repetition. - Each of the 9
3x3sub-boxes of the grid must contain the digits1-9without repetition.
A partially filled sudoku which is valid.
The Sudoku board could be partially filled, where empty cells are filled with the character '.'.
Example 1:
Input:
[
["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
Output: true
Example 2:
Input:
[
["8","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being
modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.
Note:
- A Sudoku board (partially filled) could be valid but is not necessarily solvable.
- Only the filled cells need to be validated according to the mentioned rules.
- The given board contain only digits
1-9and the character'.'. - The given board size is always
9x9.
题目大意
判断一个 9x9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
- 数字 1-9 在每一行只能出现一次。
- 数字 1-9 在每一列只能出现一次。
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
解题思路
以下是每个版本的解题思路的详细介绍:
Go 版本解题思路
-
创建三个二维布尔数组:
rowbuf、colbuf、boxbuf,分别用于缓存每行、每列和每个3x3的方框中数字是否已经出现。 -
遍历数独棋盘,检查每个格子:
- 如果格子包含字符
'.',则跳过不处理。 - 如果格子包含数字字符,将其转换为整数并检查是否已经在当前行、列或3x3方框中出现过。
- 如果已经出现过,则返回
false,表示数独无效。 - 否则,将更新缓存数组,标记该数字已经出现。
- 如果格子包含字符
-
如果通过上述检查,返回
true,表示数独是有效的。
Python 版本解题思路
-
创建三个二维布尔数组:
row_used、col_used、cell_used,用于记录每行、每列和每个3x3单元格中数字的出现情况。 -
遍历数独棋盘,检查每个格子:
- 如果格子包含字符
'.',则跳过不处理。 - 如果格子包含数字字符,将其转换为整数,并检查是否已经在当前行、列或3x3单元格中出现过。
- 如果已经出现过,则返回
false,表示数独无效。 - 否则,标记该数字在当前行、列和单元格中已经出现。
- 如果格子包含字符
-
如果通过上述检查,返回
true,表示数独是有效的。
ava 版本解题思路
-
创建三个二维布尔数组:
rowbuf、colbuf、boxbuf,分别用于缓存每行、每列和每个3x3的方框中数字是否已经出现。 -
遍历数独棋盘,检查每个格子:
- 如果格子包含字符
'.',则跳过不处理。 - 如果格子包含数字字符,将其转换为整数,并检查是否已经在当前行、列或3x3方框中出现过。
- 如果已经出现过,则返回
false,表示数独无效。 - 否则,将更新缓存数组,标记该数字已经出现。
- 如果格子包含字符
-
如果通过上述检查,返回
true,表示数独是有效的。
C++ 版本解题思路
-
创建三个二维整数数组:
row、column、box,用于跟踪每行、每列和每个3x3方框中数字的出现情况。 -
遍历数独棋盘,检查每个格子:
- 如果格子包含字符
'.',则跳过不处理。 - 如果格子包含数字字符,将其转换为整数并检查是否已经在当前行、列或3x3方框中出现过。
- 如果已经出现过,则返回
false,表示数独无效。 - 否则,将更新相应的计数器,标记该数字已经出现。
- 如果格子包含字符
-
如果通过上述检查,返回
true,表示数独是有效的。
代码
Go
func isValidSudoku1(board [][]byte) bool {
// 创建三个二维布尔数组,用于缓存每行、每列和每个3x3的方框中数字是否已经出现
rowbuf, colbuf, boxbuf := make([][]bool, 9), make([][]bool, 9), make([][]bool, 9)
for i := 0; i < 9; i++ {
rowbuf[i] = make([]bool, 9)
colbuf[i] = make([]bool, 9)
boxbuf[i] = make([]bool, 9)
}
// 遍历一次,添加缓存
for r := 0; r < 9; r++ {
for c := 0; c < 9; c++ {
if board[r][c] != '.' {
// 将字符数字转换为整数
num := board[r][c] - '0' - byte(1)
// 检查行、列和3x3方格中是否已经出现相同的数字
if rowbuf[r][num] || colbuf[c][num] || boxbuf[r/3*3+c/3][num] {
return false
}
// 更新缓存数组,标记数字已经出现
rowbuf[r][num] = true
colbuf[c][num] = true
boxbuf[r/3*3+c/3][num] = true // r,c 转换到box方格中
}
}
}
// 如果通过上述检查,则数独有效
return true
}
Python
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
row_used = [[False] * 9 for _ in range(9)] # 记录每一行出现过的数字
col_used = [[False] * 9 for _ in range(9)] # 记录每一列出现过的数字
cell_used = [[False] * 9 for _ in range(9)] # 记录每一个单元格出现过的数字
for r in range(9):
for c in range(9):
if board[r][c] == '.': continue # 不为数字的位置跳过处理
char_id = int(board[r][c]) - 1 # 获取数字对应的编号(索引)
# 检查当前数字是否已经在当前行、当前列或当前单元格中出现过
if row_used[r][char_id] or col_used[c][char_id] or cell_used[r // 3 * 3 + c // 3][char_id]:
return False # 如果出现重复,则数独无效
# 否则标记该数字出现过
row_used[r][char_id], col_used[c][char_id], cell_used[r // 3 * 3 + c // 3][char_id] = True, True, True
return True # 如果通过了所有检查,数独是有效的
Java
class Solution {
public boolean isValidSudoku(char[][] board) {
boolean[][] rowbuf = new boolean[9][9];
boolean[][] colbuf = new boolean[9][9];
boolean[][] boxbuf = new boolean[9][9];
// 遍历一次,添加缓存
for (int r = 0; r < 9; r++) {
for (int c = 0; c < 9; c++) {
if (board[r][c] != '.') {
int num = board[r][c] - '1';
// 检查行
if (rowbuf[r][num]) {
return false;
}
rowbuf[r][num] = true;
// 检查列
if (colbuf[c][num]) {
return false;
}
colbuf[c][num] = true;
// 检查3x3的方框
int boxIndex = (r / 3) * 3 + c / 3;
if (boxbuf[boxIndex][num]) {
return false;
}
boxbuf[boxIndex][num] = true;
}
}
}
return true;
}
}
Cpp
class Solution {
public:
bool isValidSudoku(vector>& board) {
int row[9][9] = {0}; // 用于跟踪每一行中数字的出现次数
int column[9][9] = {0}; // 用于跟踪每一列中数字的出现次数
int box[9][9] = {0}; // 用于跟踪每个3x3方框中数字的出现次数
// 遍历数独棋盘
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
int box_index = i / 3 * 3 + j / 3; // 计算当前单元格属于哪个3x3方框
int temp = board[i][j] - '0' - 1; // 将字符数字转换为整数,范围是0到8
if (temp == -1) continue; // 如果是'.',跳过当前单元格
// 检查当前数字是否已经在当前行、当前列或当前方框中出现过
if (row[i][temp] == 1 || column[j][temp] == 1 || box[box_index][temp] == 1) {
return false; // 如果出现重复,则数独无效
}
// 更新相应的计数器
++row[i][temp];
++column[j][temp];
++box[box_index][temp];
}
}
return true; // 如果通过了所有检查,数独是有效的
}
};
当涉及到不同编程语言版本的解决方案时,你需要了解一些基本概念和语法,以便理解代码的工作原理。以下是每个版本的详细基础知识要点:
Go 版本
-
数组和切片: Go 中的数组是固定长度的,切片则是可变长度的。在本解决方案中,使用了切片来存储行、列和方框的数字出现情况。
-
二维数组: Go 支持多维数组,因此可以轻松地创建二维数组来表示数独的棋盘和数字出现情况。
-
循环: 使用
for循环遍历二维数组中的所有元素,这在解决数独问题时非常有用。 -
条件语句: 使用
if条件语句来检查数字是否已经出现,并根据条件做出相应的处理。 -
类型转换: 代码中使用了字符到整数的类型转换,将字符数字转换为整数以进行索引。
Python 版本
-
列表: Python 中的列表(List)是可变序列,用于存储数独的棋盘和数字出现情况。
-
二维列表: 通过嵌套列表,可以轻松地表示二维数据结构,例如数独棋盘和数字出现情况。
-
循环: 使用
for循环遍历二维列表中的所有元素,这在解决数独问题时非常有用。 -
条件语句: 使用
if条件语句来检查数字是否已经出现,并根据条件做出相应的处理。 -
类型转换: 代码中使用了字符到整数的类型转换,将字符数字转换为整数以进行索引。
-
面向对象编程: 解决方案使用了面向对象编程的风格,将检查数独有效性的逻辑封装在一个类中。
ava 版本
-
数组: Java 中的数组是固定长度的,可以用于存储数独的棋盘和数字出现情况。
-
二维数组: 使用二维数组来表示数独棋盘和数字出现情况。
-
循环: 使用
for循环遍历二维数组中的所有元素,这在解决数独问题时非常有用。 -
条件语句: 使用
if条件语句来检查数字是否已经出现,并根据条件做出相应的处理。 -
类型转换: 代码中使用了字符到整数的类型转换,将字符数字转换为整数以进行索引。
C++ 版本
-
数组: C++ 中的数组是固定长度的,可以用于存储数独的棋盘和数字出现情况。
-
二维数组: 使用二维数组来表示数独棋盘和数字出现情况。
-
循环: 使用
for循环遍历二维数组中的所有元素,这在解决数独问题时非常有用。 -
条件语句: 使用
if条件语句来检查数字是否已经出现,并根据条件做出相应的处理。 -
类型转换: 代码中使用了字符到整数的类型转换,将字符数字转换为整数以进行索引。
了解这些基础知识点可以帮助你理解每个版本的代码是如何实现数独验证的。此外,还需要了解数组和循环的基本概念,以便更好地理解代码的工作原理。
37. Sudoku Solver
题目
Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfyall of the following rules:
- Each of the digits
1-9must occur exactly once in each row. - Each of the digits
1-9must occur exactly once in each column. - Each of the the digits
1-9must occur exactly once in each of the 93x3sub-boxes of the grid.
Empty cells are indicated by the character'.'.
A sudoku puzzle…
…and its solution numbers marked in red.
Note:
- The given board contain only digits
1-9and the character'.'. - You may assume that the given Sudoku puzzle will have a single unique solution.
- The given board size is always
9x9.
题目大意
编写一个程序,通过已填充的空格来解决数独问题。一个数独的解法需遵循如下规则:
- 数字 1-9 在每一行只能出现一次。
- 数字 1-9 在每一列只能出现一次。
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 '.'表示。
解题思路
Go版本解题思路:
-
定义结构体和数据结构:首先,定义一个结构体
position用于表示数独中的位置(行和列)。创建一个空的position切片,用于存储待填入数字的位置信息。还需要定义一个布尔变量find用于表示是否找到解。 -
遍历数独格子:遍历数独的每个格子,如果当前格子是’.',表示需要填入数字,将其位置信息加入
position切片。 -
DFS暴力回溯枚举:使用深度优先搜索(DFS)进行暴力回溯枚举。在每个空格位置,尝试填入数字1到9,然后检查是否符合数独规则。如果符合规则,继续递归填充下一个位置。如果找到解,将
find设置为true并返回。 -
检查数独规则:在每个位置填入数字时,需要检查以下三个规则是否满足:
- 横行是否有重复数字
- 竖行是否有重复数字
- 九宫格是否有重复数字
-
回溯和重置:如果在当前位置填入数字后没有找到解,需要将该位置重置为’.',继续尝试下一个数字。
-
完成解题:当找到一组解时,设置
find为true并返回。此时不需要继续回溯。
Python版本解题思路:
Python版本的解题思路与Go版本类似,主要区别在于语法和数据结构的表示方式。具体解题思路如下:
-
定义类和方法:使用Python的类和方法来组织代码。定义一个类
Solution用于解决数独问题。 -
递归解法:采用深度优先搜索(DFS)的递归解法。创建
dfs方法,其中主要逻辑与Go版本相似。 -
位运算:使用位运算来检查数字的合法性,如按位与、按位或、按位异或等。
-
列表(List):Python中使用列表(List)来存储待填入数字的位置信息和进行判断。
-
回溯和重置:当在当前位置填入数字后没有找到解时,需要将该位置重置为’.',继续尝试下一个数字。
Java版本解题思路:
Java版本的解题思路与Python版本类似,主要区别在于语法和数据结构的表示方式。具体解题思路如下:
-
定义类和方法:Java是面向对象编程语言,因此使用类和方法的方式来组织代码。定义一个类
Solution用于解决数独问题。 -
递归解法:采用深度优先搜索(DFS)的递归解法。创建
dfs方法,其中主要逻辑与Python版本相似。 -
位运算:使用位运算来检查数字的合法性,如按位与、按位或、按位异或等。
-
列表(List):Java中使用List来存储待填入数字的位置信息和进行判断。
-
回溯和重置:当在当前位置填入数字后没有找到解时,需要将该位置重置为’.',继续尝试下一个数字。
C++版本解题思路:
C++版本的解题思路与Go、Python、Java版本类似,主要区别在于语法和数据结构的表示方式。具体解题思路如下:
-
定义类和函数:C++使用类和函数的方式来组织代码。定义一个类
Solution用于解决数独问题。 -
递归解法:采用深度优先搜索(DFS)的递归解法。创建
dfs方法,其中主要逻辑与其他版本相似。 -
位运算:使用位运算来检查数字的合法性,如按位与、按位或、按位异或等。
-
向量(Vector):C++中使用向量(Vector)来存储待填入数字的位置信息和进行判断。
-
回溯和重置:当在当前位置填入数字后没有找到解时,需要将该位置重置为’.',继续尝试下一个数字。
总的来说,无论使用哪种编程语言,解数独问题的基本思路是使用深度优先搜索(DFS)进行回溯枚举,同时利用位运算和合适的数据结构来检查和记录数字的合法性。这些思路在不同编程语言中都是通用的,只需根据语言的特点进行相应的实现。
代码
Go
// 定义一个结构体 position,表示数独中的位置(行和列)
type position struct {
x int // 行
y int // 列
}
// 主函数,用于解数独
func solveSudoku(board [][]byte) {
// 创建一个空的 position 切片,用于存储待填入数字的位置信息
pos, find := []position{}, false
// 遍历数独的每个格子
for i := 0; i < len(board); i++ {
for j := 0; j < len(board[0]); j++ {
// 如果当前格子是'.',表示需要填入数字,将其位置信息加入 pos 切片
if board[i][j] == '.' {
pos = append(pos, position{x: i, y: j})
}
}
}
// 调用 putSudoku 函数来填充数独
putSudoku(&board, pos, 0, &find)
}
// 递归函数,用于填充数独
func putSudoku(board *[][]byte, pos []position, index int, succ *bool) {
// 如果已经成功找到解决方案,则返回
if *succ == true {
return
}
// 如果已经遍历完了所有待填入的位置,则表示找到了解决方案
if index == len(pos) {
*succ = true
return
}
// 尝试填入数字 1 到 9
for i := 1; i < 10; i++ {
// 检查当前位置是否可以填入数字 i,同时确保还没有找到解决方案
if checkSudoku(board, pos[index], i) && !*succ {
// 填入数字 i
(*board)[pos[index].x][pos[index].y] = byte(i) + '0'
// 递归调用 putSudoku 函数,继续填充下一个位置
putSudoku(board, pos, index+1, succ)
// 如果已经找到解决方案,返回
if *succ == true {
return
}
// 如果在当前位置填入数字 i 后没有找到解决方案,则将其重置为'.',继续尝试下一个数字
(*board)[pos[index].x][pos[index].y] = '.'
}
}
}
// 检查当前位置是否可以填入指定的数字
func checkSudoku(board *[][]byte, pos position, val int) bool {
// 判断横行是否有重复数字
for i := 0; i < len((*board)[0]); i++ {
if (*board)[pos.x][i] != '.' && int((*board)[pos.x][i]-'0') == val {
return false
}
}
// 判断竖行是否有重复数字
for i := 0; i < len((*board)); i++ {
if (*board)[i][pos.y] != '.' && int((*board)[i][pos.y]-'0') == val {
return false
}
}
// 判断九宫格是否有重复数字
posx, posy := pos.x-pos.x%3, pos.y-pos.y%3
for i := posx; i < posx+3; i++ {
for j := posy; j < posy+3; j++ {
if (*board)[i][j] != '.' && int((*board)[i][j]-'0') == val {
return false
}
}
}
// 如果以上条件都不满足,说明可以填入该数字
return true
}
Python
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
# 定义翻转位的函数,用于更新行、列和块的状态
def flip(i: int, j: int, digit: int):
line[i] ^= (1 << digit)
column[j] ^= (1 << digit)
block[i // 3][j // 3] ^= (1 << digit)
# 深度优先搜索函数
def dfs(pos: int):
nonlocal valid
if pos == len(spaces): # 如果所有空格都填满了,找到了解
valid = True
return
i, j = spaces[pos] # 获取当前空格的坐标
# 计算当前可以填入的数字的掩码
mask = ~(line[i] | column[j] | block[i // 3][j // 3]) & 0x1ff
while mask:
digitMask = mask & (-mask) # 获取最低位的1
digit = bin(digitMask).count("0") - 1 # 计算数字
flip(i, j, digit) # 更新状态
board[i][j] = str(digit + 1) # 填入数字
dfs(pos + 1) # 递归下一个空格
flip(i, j, digit) # 恢复状态
mask &= (mask - 1) # 去掉最低位的1
if valid:
return
line = [0] * 9 # 记录每一行的数字状态
column = [0] * 9 # 记录每一列的数字状态
block = [[0] * 3 for _ in range(3)] # 记录每个块的数字状态
valid = False # 记录是否找到解
spaces = list() # 记录所有空格的坐标
# 遍历数独,初始化状态
for i in range(9):
for j in range(9):
if board[i][j] != ".":
digit = int(board[i][j]) - 1
flip(i, j, digit)
# 不断尝试填充数字,直到不能再填充为止
while True:
modified = False
for i in range(9):
for j in range(9):
if board[i][j] == ".":
mask = ~(line[i] | column[j] | block[i // 3][j // 3]) & 0x1ff
if not (mask & (mask - 1)): # 如果mask中只有一个1,即只有一种可能的数字
digit = bin(mask).count("0") - 1
flip(i, j, digit)
board[i][j] = str(digit + 1)
modified = True
if not modified:
break # 如果没有发生改变,说明无法再填充了
# 找到所有空格的坐标
for i in range(9):
for j in range(9):
if board[i][j] == ".":
spaces.append((i, j))
dfs(0) # 开始深度优先搜索,填充剩余的空格
Java
class Solution {
private int[] line = new int[9]; // 记录每一行的数字状态
private int[] column = new int[9]; // 记录每一列的数字状态
private int[][] block = new int[3][3]; // 记录每个块的数字状态
private boolean valid = false; // 记录是否找到解
private List spaces = new ArrayList(); // 记录所有空格的坐标
public void solveSudoku(char[][] board) {
// 初始化行、列和块的状态
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] != '.') {
int digit = board[i][j] - '0' - 1;
flip(i, j, digit);
}
}
}
// 不断尝试填充数字,直到不能再填充为止
while (true) {
boolean modified = false;
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;
if ((mask & (mask - 1)) == 0) { // 如果mask中只有一个1,即只有一种可能的数字
int digit = Integer.bitCount(mask - 1);
flip(i, j, digit);
board[i][j] = (char) (digit + '0' + 1);
modified = true;
}
}
}
}
if (!modified) {
break; // 如果没有发生改变,说明无法再填充了
}
}
// 找到所有空格的坐标
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
spaces.add(new int[]{i, j});
}
}
}
dfs(board, 0); // 开始深度优先搜索,填充剩余的空格
}
public void dfs(char[][] board, int pos) {
if (pos == spaces.size()) { // 如果所有空格都填满了,找到了解
valid = true;
return;
}
int[] space = spaces.get(pos);
int i = space[0], j = space[1];
int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;
for (; mask != 0 && !valid; mask &= (mask - 1)) {
int digitMask = mask & (-mask);
int digit = Integer.bitCount(digitMask - 1);
flip(i, j, digit);
board[i][j] = (char) (digit + '0' + 1);
dfs(board, pos + 1);
flip(i, j, digit);
}
}
public void flip(int i, int j, int digit) {
line[i] ^= (1 << digit);
column[j] ^= (1 << digit);
block[i / 3][j / 3] ^= (1 << digit);
}
}
Cpp
class Solution {
public:
void solveSudoku(vector>& board) {
vector line(9, 0); // 记录每一行的数字状态
vector column(9, 0); // 记录每一列的数字状态
vector> block(3, vector(3, 0)); // 记录每个块的数字状态
bool valid = false; // 记录是否找到解
vector> spaces; // 记录所有空格的坐标
// 初始化行、列和块的状态
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] != '.') {
int digit = board[i][j] - '0' - 1;
flip(line, column, block, i, j, digit);
}
}
}
// 不断尝试填充数字,直到不能再填充为止
while (true) {
bool modified = false;
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;
if ((mask & (mask - 1)) == 0) { // 如果mask中只有一个1,即只有一种可能的数字
int digit = __builtin_popcount(mask - 1);
flip(line, column, block, i, j, digit);
board[i][j] = digit + '0' + 1;
modified = true;
}
}
}
}
if (!modified) {
break; // 如果没有发生改变,说明无法再填充了
}
}
// 找到所有空格的坐标
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
spaces.push_back({i, j});
}
}
}
dfs(board, line, column, block, spaces, 0, valid); // 开始深度优先搜索,填充剩余的空格
}
void dfs(vector>& board, vector& line, vector& column, vector>& block, vector>& spaces, int pos, bool& valid) {
if (pos == spaces.size()) { // 如果所有空格都填满了,找到了解
valid = true;
return;
}
pair space = spaces[pos];
int i = space.first, j = space.second;
int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;
for (; mask != 0 && !valid; mask &= (mask - 1)) {
int digitMask = mask & -mask;
int digit = __builtin_ctz(digitMask);
flip(line, column, block, i, j, digit);
board[i][j] = digit + '0' + 1;
dfs(board, line, column, block, spaces, pos + 1, valid);
flip(line, column, block, i, j, digit);
}
}
void flip(vector& line, vector& column, vector>& block, int i, int j, int digit) {
line[i] ^= (1 << digit);
column[j] ^= (1 << digit);
block[i / 3][j / 3] ^= (1 << digit);
}
};
这里分别介绍了Go、Python、Java和C++版本的知识要点:
Go版本:
-
结构体(Struct):在Go中,你会看到使用结构体(Struct)来表示数独中的位置信息,如行和列。
-
递归:解决数独问题的主要算法是深度优先搜索(DFS)递归。你需要理解递归的概念和如何在Go中实现递归函数。
-
切片(Slice):你会使用切片来存储待填入数字的位置信息和进行判断。
-
位运算:位运算是判断数字是否合法的关键。你需要了解Go中的位运算,如按位与、按位或、按位异或等操作,以及如何使用它们来检查数字的合法性。
Python版本:
-
类和方法:Python中使用类和方法的方式来组织代码。你需要了解如何定义类、方法,以及如何在类中进行数据操作。
-
递归:Python版本也使用深度优先搜索(DFS)递归来解决数独问题。了解递归的概念和如何在Python中实现递归函数是必要的。
-
位运算:位运算在Python中同样是关键,用于检查数字的合法性。你需要了解Python中的位运算操作,如按位与、按位或、按位异或等。
-
列表(List):Python中的列表用于存储待填入数字的位置信息和进行判断。
Java版本:
-
类和方法:Java是一种面向对象编程语言,你需要了解如何定义类、方法,以及如何在类中进行数据操作。
-
递归:Java版本同样使用深度优先搜索(DFS)递归来解决数独问题。了解递归的概念和如何在Java中实现递归函数是必要的。
-
位运算:位运算在Java中同样是关键,用于检查数字的合法性。你需要了解Java中的位运算操作,如按位与、按位或、按位异或等。
-
列表(List):Java中的List用于存储待填入数字的位置信息和进行判断。你需要了解如何操作List。
C++版本:
-
类和函数:C++使用类和函数的方式来组织代码。你需要了解如何定义类、函数,以及如何在类中进行数据操作。
-
递归:C++版本同样使用深度优先搜索(DFS)递归来解决数独问题。了解递归的概念和如何在C++中实现递归函数是必要的。
-
位运算:位运算在C++中同样是关键,用于检查数字的合法性。你需要了解C++中的位运算操作,如按位与、按位或、按位异或等。
-
向量(Vector):C++中的向量(Vector)类似于动态数组,用于存储待填入数字的位置信息和进行判断。你需要了解如何操作向量。
总的来说,无论你使用哪种编程语言,掌握递归、数据结构(如切片、列表、向量)的使用,以及位运算的基本概念和操作,都是解决数独问题的关键。此外,了解如何在特定编程语言中实现这些概念和操作也是必要的。
38. Count-And-Say
题目
The count-and-say sequence is a sequence of digit strings defined by the recursive formula:
countAndSay(1) = “1”
countAndSay(n) is the way you would “say” the digit string from countAndSay(n-1), which is then converted into a different digit string.
To determine how you “say” a digit string, split it into the minimal number of substrings such that each substring contains exactly one unique digit. Then for each substring, say the number of digits, then say the digit. Finally, concatenate every said digit.
For example, the saying and conversion for digit string “3322251”:
Given a positive integer n, return the nth term of the count-and-say sequence.
Example 1:
Input: n = 1
Output: “1”
Explanation: This is the base case.
Example 2:
Input: n = 4
Output: “1211”
Explanation:
countAndSay(1) = “1”
countAndSay(2) = say “1” = one 1 = “11”
countAndSay(3) = say “11” = two 1’s = “21”
countAndSay(4) = say “21” = one 2 + one 1 = “12” + “11” = “1211”
Constraints:
1 <= n <= 30
题目大意
给定一个正整数 n ,输出外观数列的第 n 项。
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
countAndSay(1) = “1”
countAndSay(n) 是对 countAndSay(n-1) 的描述,然后转换成另一个数字字符串。
前五项如下:
-
1 -
11 -
21 -
1211 -
111221
第一项是数字 1
描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 “11”
描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 “21”
描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 “1211”
描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 “111221”
要 描述 一个数字字符串,首先要将字符串分割为 最小 数量的组,每个组都由连续的最多 相同字符 组成。然后对于每个组,先描述字符的数量,然后描述字符,形成一个描述组。要将描述转换为数字字符串,先将每组中的字符数量用数字替换,再将所有描述组连接起来。
例如,数字字符串 “3322251” 的描述如下图:
示例 1:
输入:n = 1
输出:“1”
解释:这是一个基本样例。
示例 2:
输入:n = 4
输出:“1211”
解释:
countAndSay(1) = “1”
countAndSay(2) = 读 “1” = 一 个 1 = “11”
countAndSay(3) = 读 “11” = 二 个 1 = “21”
countAndSay(4) = 读 “21” = 一 个 2 + 一 个 1 = “12” + “11” = “1211”
提示:
1 <= n <= 30
解题思路
以下是每个版本的解题思路:
Go 版本解题思路
-
justify 函数:这个函数用于生成下一个 count-and-say 序列。它遍历输入字符串
s,统计连续相同字符的个数,并将个数和字符按规则拼接成新的字符串。 -
countAndSay 函数:这个函数是主函数,它生成 count-and-say 序列的第
n项。它从第一项开始,依次调用justify函数来生成下一项的字符串,重复这个过程n-1次,最后返回第n项的字符串。
Python 版本解题思路
-
countAndSay 函数:这是主函数,用于生成 count-and-say 序列的第
n项。如果n为 1,直接返回 “1”,否则递归调用countAndSay(n-1)获取前一项的字符串。 -
doSay 函数:这个函数负责生成当前项的 count-and-say 序列。它遍历输入字符串
sn,统计相邻相同字符的个数,并按规则拼接成新的字符串。
Java 版本解题思路
-
justify 方法:这个方法用于生成下一个 count-and-say 序列。它遍历输入字符串,统计连续相同字符的个数,并将个数和字符按规则拼接成新的字符串。
-
countAndSay 方法:这是主方法,用于生成 count-and-say 序列的第
n项。它从第一项开始,依次调用justify方法来生成下一项的字符串,重复这个过程n-1次,最后返回第n项的字符串。
C++ 版本解题思路
-
solution 函数:这个函数用于生成下一个 count-and-say 序列。它遍历输入字符串
s,统计连续相同字符的个数,并将个数和字符按规则拼接成新的字符串。 -
countAndSay 函数:这是主函数,用于生成 count-and-say 序列的第
n项。它从第一项开始,依次调用solution函数来生成下一项的字符串,重复这个过程n-1次,最后返回第n项的字符串。
无论使用哪个版本,核心思路都是递归生成 count-and-say 序列,其中每一项都依赖于前一项,并按照规则进行字符计数和拼接。每个版本都采用了不同的编程语言和字符串处理方法,但解题思路是相同的。
代码
Go
func justify(s string) string {
var result []byte
i := 0
for i < len(s) {
c := s[i]
count := 1
// 统计连续相同字符的个数
for i+1 < len(s) && s[i] == s[i+1] {
count++
i++
}
// 将统计结果添加到结果字符串中
result = append(result, []byte(strconv.Itoa(count))...)
result = append(result, c)
i++
}
return string(result)
}
func countAndSay(n int) string {
sequence := "1"
for i := 1; i < n; i++ {
sequence = justify(sequence)
}
return sequence
}
Python
class Solution:
def countAndSay(self, n: int) -> str:
# 基础情况:n=1时返回'1'
if n == 1:
return '1'
# 递归调用,生成前一个序列
prev_sequence = self.countAndSay(n - 1)
# 调用doSay函数生成当前序列
return self.doSay(prev_sequence)
def doSay(self, sn):
counts = [] # 存储相邻相同字符的个数
digits = [] # 存储相邻相同字符
n = len(sn)
c = 1 # 初始化字符计数为1
d = sn[0] # 初始化当前字符为第一个字符
for i in range(1, n):
if sn[i] == sn[i - 1]:
c += 1 # 如果当前字符与前一个字符相同,增加计数
else:
counts.append(c) # 如果不同,将计数和字符添加到对应的列表中
digits.append(d)
c = 1 # 重置计数为1
d = sn[i] # 更新当前字符为新字符
# 处理最后一组相同字符
counts.append(c)
digits.append(d)
# 使用列表解析将计数和字符组合成字符串
return ''.join([f'{x}{y}' for x, y in zip(counts, digits)])
Java
class Solution {
// 定义一个方法,用于将输入的字符串进行报数
public String justify(String s) {
// 创建一个 StringBuilder 对象,用于存储结果
StringBuilder result = new StringBuilder();
// 遍历输入的字符串
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i); // 获取当前字符
int sum = 1; // 初始化计数器为 1,表示至少有一个当前字符
// 如果当前字符是输入字符串的最后一个字符或者与下一个字符不同
if (i + 1 >= s.length() || c != s.charAt(i + 1)) {
result.append(sum); // 将计数器的值追加到结果中
result.append(c); // 将当前字符追加到结果中
return String.valueOf(result); // 返回结果的字符串表示
}
// 如果当前字符与下一个字符相同,继续遍历并增加计数器
while (c == s.charAt(i + 1)) {
sum++;
i++;
// 如果当前字符是输入字符串的最后一个字符,将计数器的值和字符追加到结果中,并返回
if (i + 1 >= s.length()) {
result.append(sum);
result.append(c);
return String.valueOf(result);
}
}
// 将计数器的值和字符追加到结果中
result.append(sum);
result.append(c);
}
// 返回结果的字符串表示
return String.valueOf(result);
}
// 定义一个方法,根据输入的 n 返回第 n 个报数序列
public String countAndSay(int n) {
String[] list = new String[n];
list[0] = "1"; // 第一个序列是固定的 "1"
// 生成第 2 到第 n 个序列
for (int i = 1; i < n; i++) {
String s = list[i - 1]; // 获取前一个序列
list[i] = justify(s); // 生成当前序列并保存
}
// 返回第 n 个序列
return list[n - 1];
}
}
Cpp
#include
#include
class Solution {
public:
string countAndSay(int n) {
string s = "1"; // 初始序列为 "1"
for (int i = 1; i < n; ++i) {
solution(s); // 调用 solution 函数生成下一个序列
std::cout << "s:" << s << std::endl; // 可选:打印当前序列,用于调试
}
return s; // 返回第 n 个报数序列
}
void solution(string &s) {
string ans; // 用于存储生成的下一个序列
int l = 0, r = 0; // 左右指针,用于统计相同字符的个数
while (r < s.size()) {
if (s[r] == s[l]) {
r++; // 同字符,右指针移动
continue;
}
int cnt = r - l; // 统计相同字符的个数
ans.push_back(cnt + '0'); // 将个数添加到结果字符串
ans.push_back(s[l]); // 添加字符本身
l = r; // 左指针移到右指针位置
}
int cnt = r - l; // 处理末尾相同字符
ans.push_back(cnt + '0');
ans.push_back(s[l]);
s = ans; // 更新原始字符串为下一个序列
}
};
当我们用不同的编程语言来解决同一个问题时,需要了解每种语言的特定语法和库函数,但在解决这个特定问题时,需要掌握一些共同的基础知识。以下是对每个版本的详细基础知识的介绍:
Go 版本
- 函数声明与调用:了解如何声明和调用函数,以及函数的参数和返回值。
- 字符串处理:Go中字符串是不可变的,因此需要了解如何在不可变字符串上执行操作,以及如何将字符串转换为字节数组和反之。
- 循环和条件语句:了解如何使用循环和条件语句来控制程序的流程。
- 切片(Slice):切片是动态数组,需要了解如何创建和操作切片。
- 整数转字符串:Go中将整数转换为字符串的方法。
Python 版本
- 类与方法:Python是面向对象的语言,了解如何定义类和方法。
- 递归:在解决这个问题中,使用递归来生成序列的下一项。
- 字符串操作:Python提供了丰富的字符串操作方法,如索引、切片和字符串拼接。
- 列表解析:Python中的列表解析是一种快速生成列表的方式,对于处理字符计数和字符拼接很有用。
Java 版本
- 类与方法:Java是面向对象的语言,了解如何定义类和方法,并且如何使用它们来组织代码。
- 递归:与Python版本一样,Java版本也使用递归来生成序列。
- 字符串操作:Java提供了各种字符串操作方法,如charAt、length等。
- StringBuilder类:在Java中,使用StringBuilder类来构建和操作可变字符串,以提高性能。
C++ 版本
- 类与方法:C++也支持面向对象编程,了解如何定义类和成员函数。
- 递归:与Python和Java版本一样,C++版本也使用递归来生成序列。
- 字符串操作:C++提供了标准库中的string类,了解如何使用它来处理字符串。
- 字符转换:使用字符转换函数将整数转换为字符。
39. Combination Sum
题目
Given a set of candidate numbers (candidates) (without duplicates) and a target number (target), find all unique combinations in candidates where the candidate numbers sums to target.
The same repeated number may be chosen from candidates unlimited number of times.
Note:
- All numbers (including
target) will be positive integers. - The solution set must not contain duplicate combinations.
Example 1:
Input: candidates = [2,3,6,7], target = 7,
A solution set is:
[
[7],
[2,2,3]
]
Example 2:
Input: candidates = [2,3,5], target = 8,
A solution set is:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
题目大意
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
解题思路
以下是每个版本的解题思路的详细介绍:
Go 版本解题思路:
-
切片初始化:创建两个切片,
ret用于存储最终结果,vals用于存储当前组合的临时值。 -
排序:对候选数集合
candidates进行升序排序,这样可以在后续搜索中更方便地控制元素的使用。 -
递归搜索:定义名为
backtracking的递归函数,它有三个参数:start表示从候选数集合的哪个位置开始搜索,sum表示当前组合的元素和。 -
递归搜索逻辑:在
backtracking函数内部,首先检查sum是否等于 0。如果等于 0,说明找到了一个满足条件的组合,将当前的组合vals复制到一个临时切片中,并将该切片添加到结果ret中。 -
遍历候选数集合:使用循环遍历候选数集合,从
start开始,逐个考虑每个候选数。- 如果当前候选数大于
sum,说明后续的候选数也肯定大于sum,因此可以提前结束循环(剪枝)。 - 否则,将当前候选数添加到当前组合
vals中,然后递归调用backtracking函数,继续搜索。 - 在递归返回后,需要回溯,即将最后添加的候选数从
vals中移除,以便尝试其他组合。
- 如果当前候选数大于
-
调用递归函数:最后,在
combinationSum函数中调用backtracking函数,开始搜索组合。 -
返回结果:返回找到的所有组合,即
ret切片。
Python 版本解题思路:
Python 版本的解题思路与 Go 版本基本相同,使用了相似的递归回溯方法和排序,但代码语法和列表操作略有不同。主要思路包括:
-
列表初始化:创建两个列表,
result用于存储最终结果,current用于存储当前组合的临时值。 -
排序:对候选数列表
candidates进行排序,以便在后续搜索中更容易控制元素的使用。 -
递归搜索:定义名为
backtrack的递归函数,它有五个参数:result用于存储结果,current用于存储当前组合,candidates是排序后的候选数列表,target是目标和,start是当前搜索的起始位置。 -
递归搜索逻辑:在
backtrack函数内部,首先检查target是否等于 0。如果等于 0,说明找到了一个满足条件的组合,将当前组合current添加到结果result中。 -
遍历候选数列表:使用循环遍历候选数列表,从
start开始,逐个考虑每个候选数。- 如果当前候选数小于或等于
target,将当前候选数添加到当前组合current中,然后递归调用backtrack函数,继续搜索。 - 在递归返回后,需要回溯,即将最后添加的候选数从
current中移除,以便尝试其他组合。
- 如果当前候选数小于或等于
-
调用递归函数:在
combinationSum函数中调用backtrack函数,开始搜索组合。 -
返回结果:返回找到的所有组合,即
result列表。
Java 版本解题思路:
Java 版本的解题思路与 Python 版本相似,但使用了 Java 的 ArrayList 来存储结果和当前组合,以及 Java 的方法命名约定。主要思路包括:
-
ArrayList 初始化:创建两个
ArrayList,result用于存储最终结果,current用于存储当前组合的临时值。 -
排序:对候选数数组
candidates进行排序,以便在后续搜索中更容易控制元素的使用。 -
递归搜索:定义名为
backtrack的递归函数,它有五个参数:result用于存储结果,current用于存储当前组合,candidates是排序后的候选数数组,target是目标和,start是当前搜索的起始位置。 -
递归搜索逻辑:在
backtrack函数内部,首先检查target是否等于 0。如果等于 0,说明找到了一个满足条件的组合,将当前组合current添加到结果result中。 -
遍历候选数数组:使用循环遍历候选数数组,从
start开始,逐个考虑每个候选数。- 如果当前候选数小于或等于
target,将当前候选数添加到当前组合current中,然后递归调用backtrack函数,继续搜索。 - 在递归返回后,需要回溯,即将最后添加的候选数从
current中移除,以便尝试其他组合。
- 如果当前候选数小于或等于
-
调用递归函数:在
combinationSum函数中调用backtrack函数,开始搜索组合。 -
返回结果:返回找到的所有组合,即
result的 `ArrayList
代码
Go
func combinationSum(candidates []int, target int) [][]int {
ret := [][]int{} // 用于存储结果的二维切片
vals := []int{} // 用于存储当前组合的切片
var backtraking func(candidates []int, start, sum int) // 递归函数的声明
sort.Ints(candidates) // 对候选数集合进行升序排序
// 定义递归函数,该函数用于搜索组合
backtraking = func(candidates []int, start, sum int) {
if sum == 0 {
tmp := make([]int, len(vals)) // 创建一个临时切片以存储当前组合
copy(tmp, vals) // 将当前组合复制到临时切片中
ret = append(ret, tmp) // 将临时切片添加到结果中
return
}
for i := start; i < len(candidates); i++ {
if candidates[i] > sum {
break
}
vals = append(vals, candidates[i]) // 将当前候选数添加到组合中
backtraking(candidates, i, sum-candidates[i]) // 递归调用函数,继续搜索
vals = vals[:len(vals)-1] // 回溯,将最后一个元素从组合中移除
}
}
backtraking(candidates, 0, target) // 调用递归函数来开始搜索组合
return ret // 返回找到的所有组合
}
Python
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def backtrack(result, current, candidates, target, start):
if target == 0:
result.append(list(current))
return
for i in range(start, len(candidates)):
if candidates[i] <= target:
current.append(candidates[i])
backtrack(result, current, candidates, target - candidates[i], i)
current.pop()
result = []
current = []
# 对候选数列表进行排序
candidates.sort()
# 调用回溯函数
backtrack(result, current, candidates, target, 0)
return result
Java
import java.util.ArrayList;
import java.util.List;
import java.util.Arrays;
class Solution {
public List> combinationSum(int[] candidates, int target) {
List> result = new ArrayList<>();
List current = new ArrayList<>();
// 对候选数列表进行排序
Arrays.sort(candidates);
// 调用回溯函数
backtrack(result, current, candidates, target, 0);
return result;
}
private void backtrack(List> result, List current, int[] candidates, int target, int start) {
if (target == 0) {
result.add(new ArrayList<>(current));
return;
}
for (int i = start; i < candidates.length && candidates[i] <= target; i++) {
current.add(candidates[i]);
backtrack(result, current, candidates, target - candidates[i], i);
current.remove(current.size() - 1);
}
}
}
Cpp
class Solution {
public:
vector> combinationSum(vector& candidates, int target) {
vector> result;
vector current;
// 对候选数列表进行排序
sort(candidates.begin(), candidates.end());
// 调用回溯函数
backtrack(result, current, candidates, target, 0);
return result;
}
void backtrack(vector>& result, vector& current, vector& candidates, int target, int start) {
if (target == 0) {
result.push_back(current);
return;
}
for (int i = start; i < candidates.size() && candidates[i] <= target; i++) {
current.push_back(candidates[i]);
backtrack(result, current, candidates, target - candidates[i], i);
current.pop_back();
}
}
};
当我们用中文进行介绍时,分别介绍每个版本(Go、Python、Java 和 C++)的代码,以及为理解这些代码所需的基础知识:
Go 版本:
-
切片(Slices):Go 中的切片是动态数组,它们的长度可以根据需要增长。在这个代码中,
vals和ret都是切片,用于存储组合的临时数据和最终结果。 -
递归(Recursion):代码使用递归的方式来搜索可能的组合。了解递归的工作原理和如何编写递归函数对理解这段代码非常重要。
-
排序(Sorting):在开始组合搜索之前,代码对候选数组进行了排序。了解排序的算法和如何在 Go 中进行排序是必要的。
-
切片操作:代码使用切片的操作,如
append和切片截取,来处理组合的元素。
Python 版本:
-
列表(Lists):Python 中的列表用于存储多个值。在这个代码中,
result和current都是列表,用于存储组合的临时数据和最终结果。 -
递归(Recursion):代码使用递归的方式来搜索可能的组合。了解递归的工作原理和如何编写递归函数对理解这段代码非常重要。
-
排序(Sorting):在开始组合搜索之前,代码对候选数组进行了排序。了解排序的算法和如何在 Python 中进行排序是必要的。
-
列表操作:代码使用列表的操作,如
append和pop,来处理组合的元素。
Java 版本:
-
列表(Lists):Java 中可以使用
ArrayList或其他列表来存储多个值。在这个代码中,result和current都是ArrayList,用于存储组合的临时数据和最终结果。 -
递归(Recursion):代码使用递归的方式来搜索可能的组合。了解递归的工作原理和如何编写递归函数对理解这段代码非常重要。
-
排序(Sorting):在开始组合搜索之前,代码对候选数组进行了排序。了解排序的算法和如何在 Java 中进行排序是必要的。
-
列表操作:代码使用列表的操作,如
add和remove,来处理组合的元素。
C++ 版本:
-
向量(Vectors):C++ 中的
vector用于存储多个值。在这个代码中,result和current都是vector,用于存储组合的临时数据和最终结果。 -
递归(Recursion):代码使用递归的方式来搜索可能的组合。了解递归的工作原理和如何编写递归函数对理解这段代码非常重要。
-
排序(Sorting):在开始组合搜索之前,代码对候选数组进行了排序。了解排序的算法和如何在 C++ 中进行排序是必要的。
-
向量操作:代码使用向量的操作,如
push_back和pop_back,来处理组合的元素。
在理解这些代码的基础上,还需要了解递归、排序算法和数据结构(如列表或切片)的基础知识,以便更好地理解和修改这些代码。
40. Combination Sum II
题目
Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations
incandidateswhere the candidate numbers sums totarget.
Each number incandidatesmay only be usedoncein the combination.
Note:
- All numbers (including
target) will be positive integers. - The solution set must not contain duplicate combinations.
Example 1:
Input: candidates = [10,1,2,7,6,1,5], target = 8,
A solution set is:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
Example 2:
Input: candidates = [2,5,2,1,2], target = 5,
A solution set is:
[
[1,2,2],
[5]
]
题目大意
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
解题思路
Go 版本解题思路
-
排序候选数组: 首先,对给定的
candidates数组进行排序。这是为了方便后续去重操作,相同的元素会相邻排列。 -
使用递归进行搜索: 使用递归函数
findcombinationSum2来搜索符合条件的组合。函数的参数包括当前的candidates数组,目标值target,当前搜索的起始位置index,当前正在构建的组合c,以及结果列表res。 -
递归搜索: 在递归搜索中,首先检查是否已经达到目标值
target,如果是,则将当前组合c添加到结果列表res中。 -
遍历候选数: 遍历
candidates数组中的元素,从当前的index开始。在遍历的过程中,注意进行去重操作,如果当前元素和前一个元素相同,就跳过,以避免重复组合。 -
构建组合: 对于每个合法的候选数,将它添加到当前组合
c中,并更新目标值target。然后,递归调用findcombinationSum2函数,继续搜索。 -
回溯操作: 在递归调用返回后,需要进行回溯操作,将最后添加的候选数移出当前组合
c,以便继续搜索其他可能的组合。 -
返回结果: 最终,返回结果列表
res,其中包含了所有符合条件的唯一组合。
Python 版本解题思路
Python 版本的解题思路与 Go 版本类似,但使用了 Python 特定的语法和函数。以下是解题思路:
-
排序候选数组: 首先,对给定的
candidates列表进行排序。这是为了方便后续去重操作,相同的元素会相邻排列。 -
使用递归进行搜索: 使用递归函数
dfs来搜索符合条件的组合。函数的参数包括当前的candidates列表,目标值target,当前搜索的起始位置start,当前正在构建的组合sub,以及结果列表res。 -
递归搜索: 在递归搜索中,首先检查是否已经达到目标值
target,如果是,则将当前组合sub添加到结果列表res中。 -
遍历候选数: 遍历
candidates列表中的元素,从当前的start开始。在遍历的过程中,注意进行去重操作,如果当前元素和前一个元素相同,就跳过,以避免重复组合。 -
构建组合: 对于每个合法的候选数,将它添加到当前组合
sub中,并更新目标值target。然后,递归调用dfs函数,继续搜索。 -
回溯操作: 在递归调用返回后,需要进行回溯操作,将最后添加的候选数移出当前组合
sub,以便继续搜索其他可能的组合。 -
返回结果: 最终,返回结果列表
res,其中包含了所有符合条件的唯一组合。
Java 版本解题思路
Java 版本的解题思路与 Python 版本类似,但使用了 Java 特定的语法和集合类。以下是解题思路:
-
排序候选数组: 首先,对给定的
candidates数组进行排序。这是为了方便后续去重操作,相同的元素会相邻排列。 -
使用匿名内部类进行搜索: 使用匿名内部类来实现
AbstractList接口,该类重写了get和size方法,以便实现结果列表的惰性生成。 -
递归搜索: 在递归搜索中,首先检查是否已经达到目标值
target,如果是,则将当前组合添加到结果列表中。 -
遍历候选数: 遍历
candidates数组中的元素,从当前的起始位置开始。在遍历的过程中,注意进行去重操作,如果当前元素和前一个元素相同,就跳过,以避免重复组合。 -
构建组合: 对于每个合法的候选数,将它添加到当前组合中,并更新目标值。然后,递归调用搜索函数,继续搜索。
-
回溯操作: 在递归调用返回后,需要进行回溯操作,将最后添加的候选数移出当前组合,以便继续搜索其他可能的组合。
-
返回结果: 最终,返回结果列表,其中包含了所有符合条件的唯一组合。
C++ 版本解题思路
C++ 版本的解题思路与 Python 版本类似,但使用了 C++ 特定的语法和标准库函数。以下是解题思路:
-
排序候选数组: 首先,对给定的
candidates向量进行排序。这是为了方便后续去重操作,相同的元素会相邻排列。 -
使用递归进行搜索 (continued): 在递归搜索中,首先检查是否已经达到目标值
target,如果是,则将当前组合currentCombination添加到结果向量result中。 -
遍历候选数: 遍历
candidates向量中的元素,从当前的index开始。在遍历的过程中,注意进行去重操作,如果当前元素和前一个元素相同,就跳过,以避免重复组合。 -
构建组合: 对于每个合法的候选数,将它添加到当前组合
currentCombination中,并更新目标值target。然后,递归调用findCombinationSum2函数,继续搜索。 -
回溯操作: 在递归调用返回后,需要进行回溯操作,将最后添加的候选数移出当前组合
currentCombination,以便继续搜索其他可能的组合。 -
返回结果: 最终,返回结果向量
result,其中包含了所有符合条件的唯一组合。
代码
Go
import (
"sort"
)
func combinationSum2(candidates []int, target int) [][]int {
if len(candidates) == 0 {
return [][]int{}
}
c, res := []int{}, [][]int{}
sort.Ints(candidates) // 这里是去重的关键逻辑
findcombinationSum2(candidates, target, 0, c, &res)
return res
}
func findcombinationSum2(nums []int, target, index int, c []int, res *[][]int) {
if target == 0 {
b := make([]int, len(c))
copy(b, c)
*res = append(*res, b)
return
}
for i := index; i < len(nums); i++ {
if i > index && nums[i] == nums[i-1] { // 这里是去重的关键逻辑,本次不取重复数字,下次循环可能会取重复数字
continue
}
if target >= nums[i] {
c = append(c, nums[i])
findcombinationSum2(nums, target-nums[i], i+1, c, res)
c = c[:len(c)-1]
}
}
}
Python
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort() # 对候选数组进行排序,以便去重
res = [] # 用于存储最终结果的列表
def dfs(candidates, start, sub, subTarget):
if subTarget == 0: # 当子目标值为0时,表示找到了一个组合
res.append(sub)
return
if subTarget < 0: # 当子目标值小于0时,不符合条件,直接返回
return
for i in range(start, len(candidates)):
if candidates[i] > subTarget:
break # 剪枝:如果当前候选数大于子目标值,跳出循环
if i > start and candidates[i] == candidates[i - 1]:
continue # 去重逻辑:跳过重复的候选数
# 递归调用,尝试将当前候选数加入子组合,并更新子目标值和下一次搜索的起始位置
dfs(candidates, i + 1, sub + [candidates[i]], subTarget - candidates[i])
dfs(candidates, 0, [], target) # 初始调用 DFS
return res # 返回最终结果
Java
import java.util.AbstractList;
class Solution {
public static List> combinationSum2(int[] candidates, int target) {
return new AbstractList>() { // 创建一个继承自 AbstractList 的匿名内部类
private final List> list = new ArrayList<>(); // 存储最终结果的列表
private final List comb = new ArrayList<>(); // 存储当前组合的列表
@Override
public List get(int index) {
init(); // 初始化,确保结果列表已经生成
return list.get(index); // 返回指定索引处的组合
}
@Override
public int size() {
init(); // 初始化,确保结果列表已经生成
return list.size(); // 返回结果列表的大小
}
public void init() {
if (list.isEmpty()) { // 如果结果列表为空,进行初始化操作
Arrays.sort(candidates); // 对候选数组进行排序,以便进行去重和优化
getComb(target, 0); // 调用递归函数生成组合
}
}
public void getComb(int target, int beginIndex) {
if (target == 0) { // 当目标值为0时,表示找到一个组合
list.add(new ArrayList<>(comb)); // 将当前组合添加到结果列表中
return;
}
for (int i = beginIndex; i < candidates.length; i++) {
if (candidates[i] > target) {
return; // 剪枝:如果当前候选数大于目标值,直接返回,不再继续搜索
}
comb.add(candidates[i]); // 将当前候选数加入组合
getComb(target - candidates[i], i + 1); // 递归调用,更新目标值和起始位置
comb.remove(comb.size() - 1); // 回溯,移除最后一个候选数
while (i + 1 < candidates.length && candidates[i + 1] == candidates[i]) {
i++; // 去重逻辑:跳过重复的候选数
}
}
}
};
}
}
Cpp
class Solution {
public:
vector> combinationSum2(vector& candidates, int target) {
vector> result; // 存储最终结果的二维向量
vector currentCombination; // 存储当前组合的一维向量
if (candidates.empty()) {
return result; // 如果候选数组为空,直接返回空结果
}
sort(candidates.begin(), candidates.end()); // 对候选数组进行排序,以便进行去重和优化
findCombinationSum2(candidates, target, 0, currentCombination, result); // 调用递归函数生成组合
return result;
}
private:
void findCombinationSum2(vector& candidates, int target, int index, vector& currentCombination, vector>& result) {
if (target == 0) { // 当目标值为0时,表示找到一个组合
result.push_back(currentCombination); // 将当前组合添加到结果中
return;
}
for (int i = index; i < candidates.size(); i++) {
if (i > index && candidates[i] == candidates[i - 1]) {
continue; // 去重逻辑:跳过重复元素
}
if (target >= candidates[i]) {
currentCombination.push_back(candidates[i]); // 添加当前候选数到组合中
findCombinationSum2(candidates, target - candidates[i], i + 1, currentCombination, result); // 递归调用,更新目标值和起始位置
currentCombination.pop_back(); // 回溯,移除当前候选数
}
}
}
};
当我们分别介绍每个版本的代码时,我会详细解释每种编程语言的基础知识要求。以下是每个版本的说明:
Go 版本
Go 是一种静态类型的编程语言,如果您要理解 Go 版本的代码,需要掌握以下基础知识:
-
变量和数据类型: 了解如何声明变量和使用不同的数据类型,例如整数、切片、数组和切片等。
-
函数: 了解如何定义和调用函数,以及函数的参数和返回值。
-
切片和数组: 了解 Go 中的切片和数组,它们在此代码中用于存储组合。
-
递归: 理解递归的概念和工作原理,因为代码使用递归来查找组合。
-
排序: 理解如何使用
sort包对切片进行排序,以进行去重。 -
循环和条件语句: 理解如何使用循环和条件语句来控制程序的流程。
Python 版本
Python 是一种简单而强大的编程语言,如果您要理解 Python 版本的代码,需要掌握以下基础知识:
-
变量和数据类型: 了解如何声明变量和使用不同的数据类型,例如整数、列表和元组等。
-
函数: 了解如何定义和调用函数,以及函数的参数和返回值。
-
列表: 了解 Python 中的列表,它们在此代码中用于存储组合。
-
递归: 理解递归的概念和工作原理,因为代码使用递归来查找组合。
-
排序: 了解如何使用
sorted函数对列表进行排序,以进行去重。 -
循环和条件语句: 理解如何使用循环和条件语句来控制程序的流程。
Java 版本
-
类和对象: 了解如何定义类和创建对象,因为 Java 是面向对象的语言。
-
方法: 了解如何定义和调用方法,以及方法的参数和返回值。
-
列表和集合: 了解 Java 中的列表和集合,它们在此代码中用于存储组合。
-
递归: 理解递归的概念和工作原理,因为代码使用递归来查找组合。
-
排序: 了解如何使用
Collections.sort方法对列表进行排序,以进行去重。 -
循环和条件语句: 理解如何使用循环和条件语句来控制程序的流程。
C++ 版本
C++ 是一种多范式编程语言,如果您要理解 C++ 版本的代码,需要掌握以下基础知识:
-
变量和数据类型: 了解如何声明变量和使用不同的数据类型,例如整数、向量和数组等。
-
函数: 了解如何定义和调用函数,以及函数的参数和返回值。
-
向量和数组: 了解 C++ 中的向量和数组,它们在此代码中用于存储组合。
-
递归: 理解递归的概念和工作原理,因为代码使用递归来查找组合。
-
排序: 了解如何使用标准库的
sort函数对向量进行排序,以进行去重。 -
循环和条件语句: 理解如何使用循环和条件语句来控制程序的流程。
以上是每个版本代码所需的基础知识要求。您可以根据您的编程语言偏好选择其中一个版本,并深入学习相关的语言特性和库函数,以更好地理解和修改代码。
41. First Missing Positive
题目
Given an unsorted integer array, find the smallest missing positive integer.
Example 1:
Input: [1,2,0]
Output: 3
Example 2:
Input: [3,4,-1,1]
Output: 2
Example 3:
Input: [7,8,9,11,12]
Output: 1
Note:
Your algorithm should run in O(n) time and uses constant extra space.
题目大意
找到缺失的第一个正整数。
解题思路
Go解决方案:
这个解决方案的思路如下:
-
首先,遍历数组,将正整数放置到它们应该在的位置上。具体做法是,对于数组中的每个元素
nums[i],如果它是一个正整数并且在有效范围内(1 到 n),则将它放置到索引为nums[i] - 1的位置上。这样,数组中的正整数应该在的位置就被正确标记了。 -
然后,再次遍历数组,找到第一个不在正确位置上的正整数,即缺失的第一个正整数。如果在遍历的过程中找到了这样的正整数,就返回它。如果遍历完数组都没有找到,说明数组中包含了所有的正整数,那么返回
len(nums) + 1,即下一个正整数。 -
这个解决方案还包括一个递归函数
changeArray,用于处理交换元素的过程。
Python解决方案:
这个解决方案的思路如下:
-
首先,将数组中的所有元素存储到一个集合(set)中,以便快速查找。
-
然后,从1开始逐个检查正整数。如果某个正整数不在集合中,即为缺失的第一个正整数,直接返回它。
-
如果遍历完所有正整数都没有找到缺失的正整数,说明数组中包含了所有正整数,返回
n + 1,其中n是数组的长度。
Java解决方案:
这个解决方案的思路如下:
-
创建一个布尔数组
numExists,用于标记正整数的存在情况,数组长度为nums.length + 1。初始化时,所有元素都为false。 -
遍历数组
nums,将数组中的正整数对应的numExists中的位置标记为true。 -
再次遍历
numExists数组,找到第一个未标记为true的位置,即为缺失的第一个正整数。 -
如果遍历完
numExists数组都没有找到,说明数组中包含了所有正整数,返回nums.length + 1。
C++解决方案:
这个解决方案的思路如下:
-
首先,遍历数组,将正整数放置到它们应该在的位置上。具体做法是,对于数组中的每个元素
nums[i],如果它是一个正整数并且在有效范围内(1 到 n),则将它放置到索引为nums[i] - 1的位置上。这样,数组中的正整数应该在的位置就被正确标记了。 -
然后,再次遍历数组,找到第一个不在正确位置上的正整数,即缺失的第一个正整数。如果在遍历的过程中找到了这样的正整数,就返回它。如果遍历完数组都没有找到,说明数组中包含了所有正整数,那么返回
n + 1,即下一个正整数。
代码
Go
func firstMissingPositive(nums []int) int {
for i := 0; i < len(nums); i++ {
if nums[i] > 0 && nums[i] <= len(nums) && nums[i] != i+1 {
tmp := nums[nums[i]-1]
nums[nums[i]-1] = nums[i]
if tmp == i+1 || tmp <= 0 || tmp > len(nums) {
nums[i] = tmp
} else {
if tmp > 0 && tmp <= len(nums) && tmp != nums[tmp-1] {
tmp = changeArray(nums, tmp)
} else {
nums[i] = tmp
}
}
}
}
for i := 0; i < len(nums); i++ {
if nums[i] != i+1 {
return i + 1
}
}
return len(nums) + 1
}
func changeArray(nums []int, tmp int) int {
if tmp <= 0 || tmp > len(nums) || tmp == nums[tmp-1] {
return tmp
}
nextTmp := nums[tmp-1]
nums[tmp-1] = tmp
return changeArray(nums, nextTmp)
}
Python
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
# 使用集合来存储数组中的元素,以便快速查找
s = set(nums)
n = len(nums)
# 从1开始逐个检查正整数,如果某个正整数不在集合中,即为缺失的第一个正整数
for i in range(1, n + 1):
if i not in s:
return i
# 如果数组中包含所有正整数,则返回 n+1
return n + 1
Java
class Solution {
public int firstMissingPositive(int[] nums) {
// 创建一个映射(数组),用于存储正整数的存在情况
boolean[] numExists = new boolean[nums.length + 1];
// 将数组中的正整数标记在映射中
for (int num : nums) {
if (num > 0 && num <= nums.length) {
numExists[num] = true;
}
}
// 从1开始逐个检查映射,找到第一个未标记的正整数即为缺失的第一个正整数
for (int i = 1; i < numExists.length; i++) {
if (!numExists[i]) {
return i;
}
}
// 如果数组中包含所有正整数,则返回数组长度加1作为缺失的第一个正整数
return nums.length + 1;
}
}
Cpp
class Solution {
public:
int firstMissingPositive(vector& nums) {
int n = nums.size();
// 遍历数组,将每个正整数 nums[i] 放置到其应该在的位置 nums[nums[i]-1]
for (int i = 0; i < n; ) {
// 检查 nums[i] 是否是一个有效的正整数,并且是否不在正确的位置上
if (nums[i] > 0 && nums[i] < n && nums[i] != nums[nums[i] - 1]) {
swap(nums[i], nums[nums[i] - 1]); // 将 nums[i] 放置到正确的位置
} else {
i++;
}
}
// 再次遍历数组,找到第一个不在正确位置上的正整数,返回它
for (int i = 0; i < n; i++) {
if (nums[i] != i + 1) {
return i + 1;
}
}
// 如果数组中包含所有正整数,则返回 n+1
return n + 1;
}
};
每个版本的解决方案所需的详细基础知识。
Go解决方案:
-
基本语法: 熟悉Go编程语言的基本语法,包括变量声明、循环、条件语句等。
-
切片(Slices): 了解Go中切片的概念和用法,因为该解决方案使用了切片来操作数组元素。
-
函数声明: 理解Go函数的声明和调用方式,包括函数参数和返回值。
-
数组和切片操作: 了解如何访问和修改数组和切片的元素。
-
循环和条件语句: 理解for循环和if条件语句的使用,因为该解决方案使用了这些控制结构。
-
递归: 该解决方案中使用了递归函数来处理数组元素的交换,因此了解递归的概念和实现方式也很重要。
Python解决方案:
-
基本语法: 熟悉Python编程语言的基本语法,包括变量声明、列表、循环、条件语句等。
-
列表(Lists): 了解Python中列表的概念和用法,因为该解决方案使用了列表来存储数组元素。
-
函数定义: 理解如何定义和调用Python函数,包括函数参数和返回值。
-
集合(Sets): 了解Python中集合的概念和用法,因为该解决方案使用了集合来检查元素是否存在。
-
循环和条件语句: 了解for循环和if条件语句的使用,因为该解决方案使用了这些控制结构。
Java解决方案:
-
基本语法: 熟悉Java编程语言的基本语法,包括变量声明、数组、循环、条件语句等。
-
数组: 了解Java中数组的概念和用法,因为该解决方案使用了数组来标记正整数的存在情况。
-
函数声明: 理解如何定义和调用Java方法,包括方法参数和返回值。
-
布尔数组: 了解如何使用布尔数组来标记元素的存在情况,并了解如何遍历数组。
-
循环和条件语句: 理解for循环和if条件语句的使用,因为该解决方案使用了这些控制结构。
C++解决方案:
-
基本语法: 熟悉C++编程语言的基本语法,包括变量声明、数组、循环、条件语句等。
-
数组和向量(Vectors): 了解C++中数组和向量的概念和用法,因为该解决方案使用了数组来处理正整数。
-
函数声明: 理解如何定义和调用C++函数,包括函数参数和返回值。
-
递归: 了解递归的概念和实现方式,因为该解决方案中使用了递归函数。
-
循环和条件语句: 了解for循环和if条件语句的使用,因为该解决方案使用了这些控制结构。
42. Trapping Rain Water
题目
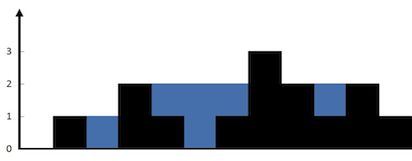
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!
Example:
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
题目大意
从 x 轴开始,给出一个数组,数组里面的数字代表从 (0,0) 点开始,宽度为 1 个单位,高度为数组元素的值。如果下雨了,问这样一个容器能装多少单位的水?
解题思路
- 每个数组里面的元素值可以想象成一个左右都有壁的圆柱筒。例如下图中左边的第二个元素 1,当前左边最大的元素是 2 ,所以 2 高度的水会装到 1 的上面(因为想象成了左右都有筒壁)。这道题的思路就是左指针从 0 开始往右扫,右指针从最右边开始往左扫。额外还需要 2 个变量分别记住左边最大的高度和右边最大高度。遍历扫数组元素的过程中,如果左指针的高度比右指针的高度小,就不断的移动左指针,否则移动右指针。循环的终止条件就是左右指针碰上以后就结束。只要数组中元素的高度比保存的局部最大高度小,就累加 res 的值,否则更新局部最大高度。最终解就是 res 的值。

- 抽象一下,本题是想求针对每个 i,找到它左边最大值 leftMax,右边的最大值 rightMax,然后 min(leftMax,rightMax) 为能够接到水的高度。left 和 right 指针是两边往中间移动的游标指针。最傻的解题思路是针对每个下标 i,往左循环找到第一个最大值,往右循环找到第一个最大值,然后把这两个最大值取出最小者,即为当前雨水的高度。这样做时间复杂度高,浪费了很多循环。i 在从左往右的过程中,是可以动态维护最大值的。右边的最大值用右边的游标指针来维护。从左往右扫一遍下标,和,从两边往中间遍历一遍下标,是相同的结果,每个下标都遍历了一次。

- 每个 i 的宽度固定为 1,所以每个“坑”只需要求出高度,即当前这个“坑”能积攒的雨水。最后依次将每个“坑”中的雨水相加即是能接到的雨水数。

以下是每个版本的解题思路:
Go 版本解题思路:
-
初始化:首先,我们初始化变量
res为 0,left为 0,right为数组height的最后一个索引,maxLeft和maxRight都为 0。 -
双指针遍历:使用一个循环来遍历
height数组,left和right分别指示当前操作的两个柱子的索引。 -
左右夹逼:在循环中,我们比较
height[left]和height[right]的高度,如果height[left]小于等于height[right],则表示左边的柱子较低。在这种情况下,我们检查height[left]是否大于maxLeft。如果是,则更新maxLeft为当前左边柱子的高度,否则将maxLeft - height[left]加到res中表示可以接到的雨水高度,并将left指针右移一位。 -
右边柱子较低:如果
height[right]小于height[left],则表示右边的柱子较低。在这种情况下,我们检查height[right]是否大于等于maxRight。如果是,则更新maxRight为当前右边柱子的高度,否则将maxRight - height[right]加到res中表示可以接到的雨水高度,并将right指针左移一位。 -
循环结束:重复执行上述步骤,直到
left不再小于等于right,这表示两个指针相遇,整个数组都被遍历完。 -
返回结果:最终,返回
res,表示可以接到的雨水总量。
Python 版本解题思路:
Python 版本的解题思路与 Go 版本基本相同,只是语法和变量声明略有不同。具体步骤如下:
-
初始化:初始化变量
res为 0,left为 0,right为数组height的最后一个索引,maxLeft和maxRight都为 0。 -
双指针遍历:使用一个循环来遍历
height数组,left和right分别指示当前操作的两个柱子的索引。 -
左右夹逼:在循环中,我们比较
height[left]和height[right]的高度,如果height[left]小于等于height[right],则表示左边的柱子较低。在这种情况下,我们检查height[left]是否大于maxLeft。如果是,则更新maxLeft为当前左边柱子的高度,否则将maxLeft - height[left]加到res中表示可以接到的雨水高度,并将left指针右移一位。 -
右边柱子较低:如果
height[right]小于height[left],则表示右边的柱子较低。在这种情况下,我们检查height[right]是否大于等于maxRight。如果是,则更新maxRight为当前右边柱子的高度,否则将maxRight - height[right]加到res中表示可以接到的雨水高度,并将right指针左移一位。 -
循环结束:重复执行上述步骤,直到
left不再小于等于right,这表示两个指针相遇,整个数组都被遍历完。 -
返回结果:最终,返回
res,表示可以接到的雨水总量。
Java 版本解题思路:
Java 版本的解题思路与 Go 和 Python 版本基本相同,只是语法和方法定义略有不同。具体步骤如下:
-
初始化:初始化变量
res为 0,left为 0,right为数组height的最后一个索引,maxLeft和maxRight都为 0。 -
双指针遍历:使用一个循环来遍历
height数组,left和right分别指示当前操作的两个柱子的索引。 -
左右夹逼:在循环中,我们比较
height[left]和height[right]的高度,如果height[left]小于等于height[right],则表示左边的柱子较低。在这种情况下,我们检查height[left]是否大于maxLeft。如果是,则更新maxLeft为当前左边柱子的高度,否则将maxLeft - height[left]加到res中表示可以接到的雨水高度,并将left指针右移一位。 -
右边柱子较低:如果
height[right]小于height[left],则表示右边的柱子较低。在这种情况下,我们检查height[right]是否大于等于maxRight。如果是,则更新maxRight为当前右边柱子的高度,否则将maxRight - height[right]加到res中表示可以接到的雨水高度,并将right指针左移一位。 -
循环结束:重复执行上述步骤,直到
left不再小于等于right,这表示两个指针相遇,整个数组都被遍历完。
6.返回结果:最终,返回 res,表示可以接到的雨水总量。
C++ 版本解题思路:
C++ 版本的解题思路与 Go、Python 和 Java 版本基本相同,只是语法和方法定义略有不同。具体步骤如下:
-
初始化:初始化变量
res为 0,left为 0,right为数组height的最后一个索引,maxLeft和maxRight都为 0。 -
双指针遍历:使用一个循环来遍历
height数组,left和right分别指示当前操作的两个柱子的索引。 -
左右夹逼:在循环中,我们比较
height[left]和height[right]的高度,如果height[left]小于等于height[right],则表示左边的柱子较低。在这种情况下,我们检查height[left]是否大于maxLeft。如果是,则更新maxLeft为当前左边柱子的高度,否则将maxLeft - height[left]加到res中表示可以接到的雨水高度,并将left指针右移一位。 -
右边柱子较低:如果
height[right]小于height[left],则表示右边的柱子较低。在这种情况下,我们检查height[right]是否大于等于maxRight。如果是,则更新maxRight为当前右边柱子的高度,否则将maxRight - height[right]加到res中表示可以接到的雨水高度,并将right指针左移一位。 -
循环结束:重复执行上述步骤,直到
left不再小于等于right,这表示两个指针相遇,整个数组都被遍历完。 -
返回结果:最终,返回
res,表示可以接到的雨水总量。
总的来说,无论使用哪种编程语言,这个问题的解决思路都是使用双指针夹逼法,动态地维护左边最大高度和右边最大高度,以便计算每个位置可以接到的雨水高度,并将其累加到结果中。最终,返回结果表示可以接到的雨水总量。不同编程语言的语法和细节略有不同,但基本思路保持一致。
代码
Go
func trap(height []int) int {
res, left, right, maxLeft, maxRight := 0, 0, len(height)-1, 0, 0
// 初始化结果res为0,left为0,right为height数组的最后一个索引,maxLeft和maxRight都为0
for left <= right {
// 使用一个循环来遍历height数组,left和right指示当前操作的两个柱子的索引
if height[left] <= height[right] {
// 如果左边的柱子高度小于等于右边的柱子
if height[left] > maxLeft {
// 如果当前左边柱子的高度大于maxLeft
maxLeft = height[left]
// 更新maxLeft为当前左边柱子的高度
} else {
res += maxLeft - height[left]
// 否则,将maxLeft与当前左边柱子的高度之差累加到结果res中
}
left++
// 左边柱子向右移动一位
} else {
// 如果右边的柱子高度小于左边的柱子
if height[right] >= maxRight {
// 如果当前右边柱子的高度大于等于maxRight
maxRight = height[right]
// 更新maxRight为当前右边柱子的高度
} else {
res += maxRight - height[right]
// 否则,将maxRight与当前右边柱子的高度之差累加到结果res中
}
right--
// 右边柱子向左移动一位
}
}
return res
// 循环结束后,返回结果res,表示可以接到的雨水总量
}
Python
class Solution:
def trap(self, height: List[int]) -> int:
res, left, right, maxLeft, maxRight = 0, 0, len(height) - 1, 0, 0
while left <= right:
if height[left] <= height[right]:
if height[left] > maxLeft:
maxLeft = height[left]
else:
res += maxLeft - height[left]
left += 1
else:
if height[right] >= maxRight:
maxRight = height[right]
else:
res += maxRight - height[right]
right -= 1
return res
Java
class Solution {
public int trap(int[] height) {
int res = 0, left = 0, right = height.length - 1, maxLeft = 0, maxRight = 0;
while (left <= right) {
if (height[left] <= height[right]) {
if (height[left] > maxLeft) {
maxLeft = height[left];
} else {
res += maxLeft - height[left];
}
left++;
} else {
if (height[right] >= maxRight) {
maxRight = height[right];
} else {
res += maxRight - height[right];
}
right--;
}
}
return res;
}
}
Cpp
class Solution {
public:
int trap(vector& height) {
int res = 0, left = 0, right = height.size() - 1, maxLeft = 0, maxRight = 0;
while (left <= right) {
if (height[left] <= height[right]) {
if (height[left] > maxLeft) {
maxLeft = height[left];
} else {
res += maxLeft - height[left];
}
left++;
} else {
if (height[right] >= maxRight) {
maxRight = height[right];
} else {
res += maxRight - height[right];
}
right--;
}
}
return res;
}
};
每个版本相关的基础知识和语法要点。我们将按照 Go、Python、Java 和 C++ 这四种编程语言来介绍各自的代码版本。
Go 版本:
-
函数定义和返回值:在 Go 中,函数的定义使用关键字
func,函数的返回值类型放在参数列表之后。例如,func trap(height []int) int定义了一个名为trap的函数,它接受一个整数切片height作为参数,并返回一个整数作为结果。 -
切片和数组:Go 中的切片(slice)类似于动态数组,但它是引用类型。在代码中,
height是一个整数切片,表示高度数组。 -
循环和条件语句:Go 使用
for循环和if条件语句来进行控制流程。在trap函数中,for循环用于遍历数组,if语句用于条件判断。 -
变量声明和赋值:Go 中的变量可以使用
var关键字声明,也可以使用短变量声明:=进行赋值。在代码中,有多个变量的声明和赋值操作,如res,left,right,maxLeft, 和maxRight。 -
数组/切片的索引访问:通过使用方括号
[]来访问数组或切片的元素。例如,height[left]表示访问height切片的left索引处的元素。
Python 版本:
-
类和方法:Python 是一种面向对象的编程语言,类似于 Go,函数是通过
def关键字定义的。在 Python 中,类方法的第一个参数通常是self,表示对实例自身的引用。 -
列表和循环:Python 中的列表(List)是一种动态数组,类似于 Go 中的切片。循环通过
for循环来实现。 -
条件语句:与 Go 一样,Python 使用
if语句来进行条件判断。 -
变量赋值:Python 使用
=运算符来进行变量赋值,如res,left,right,maxLeft, 和maxRight。
Java 版本:
-
类和方法:Java 是一种面向对象的编程语言,函数是通过
public int trap(int[] height)这样的方法定义的。方法参数和返回值都需要指定类型。 -
数组:Java 中的数组是固定大小的,而不是像 Go 和 Python 中的切片一样动态增长。
-
循环和条件语句:Java 使用
for循环和if语句来进行控制流程。 -
变量声明和赋值:Java 中的变量需要显式声明类型,并使用
=运算符进行赋值。在代码中,有多个变量的声明和赋值操作,如res,left,right,maxLeft, 和maxRight。
C++ 版本:
-
类和方法:C++ 是一种多范式编程语言,函数是通过
int trap(vector这样的方法定义的。方法参数和返回值都需要指定类型。& height) -
容器和循环:C++ 使用
vector容器来表示动态数组,类似于 Go 和 Python 中的切片和列表。循环可以使用for或while实现。 -
条件语句:与 Go、Python 和 Java 一样,C++ 使用
if语句来进行条件判断。 -
变量声明和赋值:C++ 中的变量声明通常在函数或代码块的开始处,然后可以使用
=运算符进行赋值。在代码中,有多个变量的声明和赋值操作,如res,left,right,maxLeft, 和maxRight。