【算法之LeetCode系列(8)】——双指针
双指针的使用:easy-->medium-->hard
-
-
-
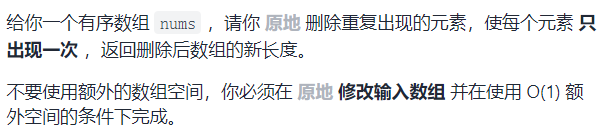
- 1. 删除有序数组中的重复项(easy)
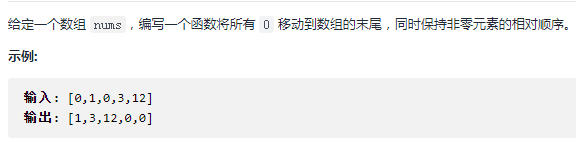
- 2. 移动零(easy)
- 3. 链表中倒数第k个节点(easy)
-
- 快慢指针小结
- 4. 两数之和 II - 输入有序数组(easy)
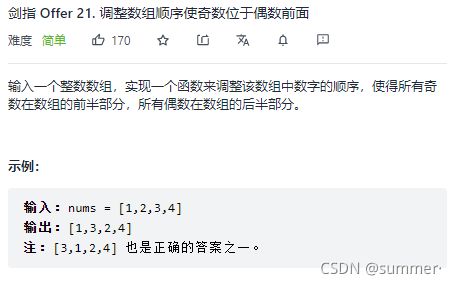
- 5.调整数组顺序使奇数位于偶数前面(easy)
- 6.和为s的两个数字(easy)
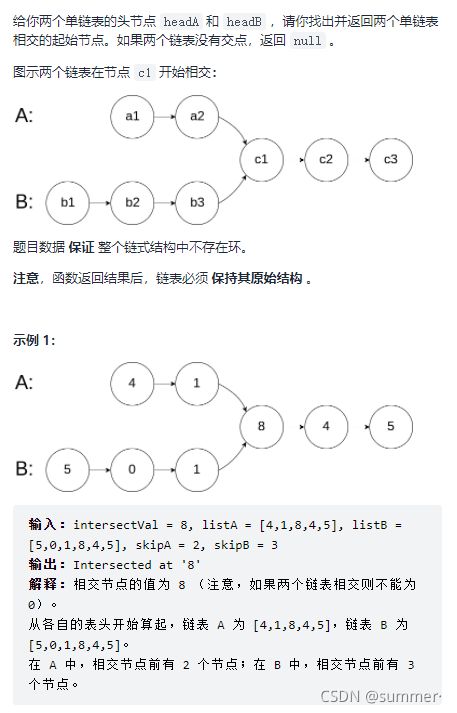
- 7.相交链表(easy)
- 8. 三数之和(medium)
- 9.盛水最多的容器(medium)
- 10.数据流中的中位数(hard)
-
-
首先,我们先来看一下双指针是什么,双指针其实是一种解题思想,指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个相同方向(快慢指针)或者相反方向(对撞指针、头尾指针、左右指针)的指针进行扫描,从而达到相应的目的。
双指针在某些特殊场合真的超级香!我们有必要学好这种思想
在开始之前,我们简单了解一下两个概念:
快慢指针:你大致理解就是一个指针每一次走的步数更多,跑的更快,另外一个指针就比这个指针走得慢(大部分情况是同向移动)
头尾指针(对撞指针、左右指针):
字面意思,就是一个指针在左(数据结构的头部),一个指针在右(数据结构的尾部),大部分情况是相向而行(双向奔赴)
先这么理解,我说的不一定是对的
1. 删除有序数组中的重复项(easy)
这个题目要求我们要原地修改数组,所以我们不能创建新的数组去保存原数组的一部分值
var removeDuplicates = function(nums) {
let len = nums.length;//获取数组的长度
if(len === 0) return 0;//如果长度为0,直接返回0,没什么好说的
let fast = 1,slow = 1;//定义快慢指针
while(fast < len){//快指针到达数组尾部时,也就是数组中的重复元素全部移除的时候
if(nums[fast] !== nums[fast - 1]){
//这里就是检测数组中有没有重复的,如果fast和fast - 1对应的值不相同
//那我就不管slow,我等到哪天我不等于我 前面 的这个重复数字的时候 ,我再把我现在这不一样的数字赋值还在很前面的slow,这样slow就要前进一步了(具体看下方图片)
nums[slow] = nums[fast];
++slow;
}
//fast持续向前走,不管上面的条件是否满足,因为你slow才有限制,我fast知识跑腿的(帮满检测有没有重复的)
++fast;
}
return slow;//最后slow就是最后一个不重复元素
};
我的图解
2. 移动零(easy)
题目中给出一个数组,数组中有若干个0,你需要将这些0全部移到数组的最后方,并且其他非0数必须保持原来的相对位置
这个题和上一个题目十分相似,大家在看题解之前,看能不能自己做出来
var moveZeroes = function(nums) {
let slow=0,fast=0
while(fast<nums.length){//同样是快指针作为边界结束条件,快指针越界表示数组中的0全部被移到后方了
if(nums[fast]!==0){//这里就和上面很像了,只不过条件是只要fast不等于0
swap(nums,slow,fast)//那么fast指向的数字就跑到slow那里,slow指向的0跑到fast那里
slow++//slow向前走
}
fast++;//不管fast指向的值是不是为0,fast继续前进
}
};
function swap(nums,l,r){//交换fast和slow指向的值
let temp=nums[r]
nums[r]=nums[l]
nums[l]=temp
}
3. 链表中倒数第k个节点(easy)
大家注意,链表是不能直接知道元素下标的,那思考一下,怎么才能知道哪个是倒数第k个节点呢?
我相信大家第一想到的是计数法,这很直观,定义一个指针,每走一步,计数加一,最后往回走,计数自减k次就OK了
但是你有没有想过,假设链表长度为5,k为4,那你是不是要遍历两次链表的长度呢?有没有更好的办法?
我们使用两个指针,一个指针(fast)先走到k+1出节点,另外一个指针(slow),还在头结点,那么
两个指针之间是不是就隔着k个节点,你再让两个指针同时向前走,这样fast指针走到表尾的时候,slow对应的节点不就是倒数第k个节点嘛(具体看下面代码)
var getKthFromEnd = function(head, k) {
let fast = head, slow = head;//先让fast和slow指向头结点
while (fast && k > 0) {//只要fast节点没到表尾且k大于0,fast就一直前进,一直到k+1个节点
fast = fast.next;//fast向前走
k = k - 1;//k 自减,控制fast向前走k次
}
while (fast) {//fast没到表尾的时候
fast = fast.next;//fast向前走
slow = slow.next;//slow向前走
}
return slow;//fast到表尾的时候,slow就是倒数第k个节点
};
快慢指针小结
前面三个题都快慢指针的简单应用,其实快慢指针的用处还有很多,特别是在链表中寻找位置这种场景
比如一个链表找最中间的节点,可以定义快指针,快指针每次走两步,慢指针每次走一步,这样,快指针走到表尾的时候,慢指针就在链表的最中间了。
需要注意的是,快慢指针一般需要同向而行,你可以想什么时候位置不能通过索引进行搜索,就可以试着想一下快慢指针的思想
4. 两数之和 II - 输入有序数组(easy)
不要被题目最后那个返回值的要求给限制了,你只需要在数组中找到两个元素,他们的值的和是目标值,就OK了,无非最后坐标加一而已
这个题大家很容易就可以想到双层循环,很快就解决了,但是双循环需要的时间复杂度是O(n*n),有没有什么更好的办法呢
这样想:反正就是两个数相加,而且数组是递增的,你“随便”找两个数相加,如果和大于target,那你就找两个位于你刚刚相加的数的左边的数加一下试试呗(有点拗口),反正题目说至少有一个答案,所以,你完全不必担心找不到。
好了,进入正题,我们可以定义两个指针,初始时,一个在数组的最左边,一个在数组的最右边,做左边代表数组最小的数,最右边代表数组最大的数,每次都让这两个指针指向的值相加,如果大于target那右指针就向左移动一个位置,如果小于target,左指针就向右移一个位置,等于target直接返回左右指针就好了(看下面具体操作)
我的图解
var twoSum = function(numbers, target) {
let l = 0;//左指针指向数组的头部(最左边)
let r = numbers.length - 1;//右指针指向数组的尾部(最右边)
while(l < r){//只要左指针在右指针的左边
if(numbers[l] + numbers[r] === target) return [l + 1, r + 1];//相等就返回当前下标加一(根据题目要求)
else if(numbers[l] + numbers[r] < target) l ++;//如果小于target,左指针右移(数组递增,所以右移一步,下次和右指针的值相加就会变大)
else r --;//同理,只要大于target,右指针左移,下次和左指针的值相加就会减小(越来越接近target)
}
};
使用左右指针,我们最多需要遍历n个元素(最中间的两个数),所以复杂度为O(n)
有童鞋说可以使用二分,当然,你可以去试试(双指针:我是双指针专题,别抢我位置!)
5.调整数组顺序使奇数位于偶数前面(easy)
这个题,我感觉大多数人第一时间都可以想到使用两个数组的办法去做,很明了,因为一个数组存奇数、一个数组存偶数,最后合并就欧了,双数组这明显很浪费空间啊,而且也很费时间。有没有更好的办法呢
这不是有双指针吗,这个题使用双指针直接原地修改,真香!(使用左右指针)具体看下方代码注释,很精妙的解法。
var exchange = function(nums) {
//首先,定义两个指针,一个指向数组的头(最左边),一个指向数组的尾(最右边)
let l = 0,r = nums.length - 1,temp;
//老套路,只要左指针小于右指针,就可以接着操作
while(l < r){
//下面的第一个while意思是,检测左指针的值是不是奇数,如果不是,那你就得把他丢后面去(跳出while,进行值交换)
//如果是奇数,左指针就向前走一步,接着检测
while(l < r && (nums[l] % 2) === 1) l ++;
//第二个循环意思是,检测右指针的值是不是偶数,如果不是,那你就得把他丢前面去(跳出while,进行值交换)
while(l < r && (nums[r] % 2) === 0) r --;
temp = nums[l];//值交换
nums[l] = nums[r];
nums[r] = temp;
}
return nums;
};
6.和为s的两个数字(easy)
此题和第四题几乎一样,给一下答案就好了 ^ - ^
我这里改用head和tail,其实和左右一个意思,指向最左边和最右边
var twoSum = function(nums, target) {
let head = 0,tail = nums.length - 1;
while(head < tail){
let sum = nums[head] + nums[tail];
if(sum < target) head ++;
if(sum > target) tail --;
if(sum === target) return [nums[head],nums[tail]];
}
return [];
};
7.相交链表(easy)
这个题的设计也很精巧,解题的想法可以这样:假定A的节点个数为A,B的节点个数为B,公共部分的节点个数为C,那么,除去公共节点,A、B的节点个数分别为(A - C)和 (B- C),你这样想,A把自己的节点走完了,跑到B的头部去,B把自己的节点走完了,跑到A的头部去,A再走(B - C)B再走(A - C),这样A、B各自走得的总节点数分别为:A + (B - C) 和 B + (A - C),你看这样,两个人是不是走得一样多呀,而且刚好,两个都走到了公共节点的地方,有点像猫抓老鼠,就两条路,(按照刚刚的走法)总会走到交点处。
var getIntersectionNode = function(headA, headB) {
let h1 = headA;//h1 在A的头部
let h2 = headB;//h2 在B的头部
while(h1 !== h2){// h1和h2 没有碰头之前,也就是没有到达公共交点之前
h1 = h1 === null ? headB : h1.next;//h1在没有走到A的尾部之前,一直向前走,走完了尾部,就直接跑到B的头部去
h2 = h2 === null ? headA : h2.next;//h2在没有走到B的尾部之前,一直向前走,走完了尾部,就直接跑到A的头部去
}
return h1;//最后相遇才会跳出循环,返回h1或者h2都可以
};
从下面开始就是中等难度的了@ - @
8. 三数之和(medium)
这个题看似和两数之和就多了一个数,但是实际复杂很多
大致思路:
首先,肯定进行排序,因为排序完了,“找和” 更容易知道下一步的移动方向
接着,遍历这个数组,遍历之前,定义两个指针,两个指针在当前遍历元素的右区间,即:左指针在当前元素的下一个,右指针在最右边,这样每次将当前元素和左右指针对应的元素求和,和0比较,如果大于0,说明数太大,那么右指针就得左移,小于0,说明数太小,左指针就得右移,直到找到等于0的三个数,将其放入数组中(这里你得检查一下,看左右指针的相邻元素是否和他们相等,相等就跳过去,去掉重复的)
var threeSum = function(nums) {
let len = nums.length;
let result = [];//保存最后的结果
if(nums == null || len < 3) return result;//小于三个的直接返回就行
nums.sort((a,b) => a-b);//对数组排序,从小到大
for(let i = 0; i < len; i++){//遍历数组
if(nums[i] > 0) break;
//这里很好理解,当前元素都大于0了,后面的所有元素都大于0,怎么可能还有三数之和为0的存在呢
if(i > 0 && nums[i] == nums[i - 1]) continue;//重复元素,直接跳过
let l = i + 1;//左指针指向当前元素右边区间的最左侧
let r = len - 1;//右指针指向当前元素右区间的最右侧
while(l < r){//老套路
const sum = nums[i] + nums[l] + nums[r];//对三数求和
if(sum == 0){//如果和为0
result.push([nums[i],nums[l],nums[r]]);//先把结果放进去
while(l < r && nums[l] === nums[l + 1]) l ++;//考虑重复的,直接跳过重复元素
while(l < r && nums[r] === nums[r - 1]) r --;//和上面一样,去掉重复的
//有符合的,那就向中间收缩区间,得继续找呀
l ++;
r --;
}
if(sum < 0) l ++;//小于0 ,左指针得右移,让整体的和变大
if(sum > 0) r --;//大于0 ,右指针得左移,让整体的和变小
}
}
return result;
};
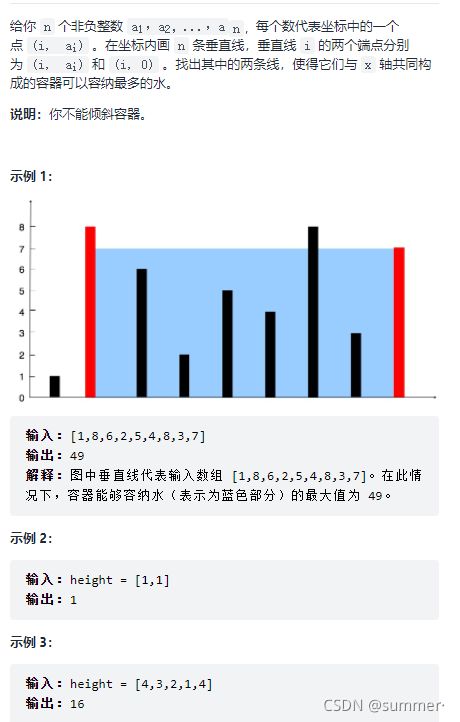
9.盛水最多的容器(medium)
我个人觉得,这其实就是找最大的面积,底(以下称宽) * 高 = 面积,找到最大面积就行了:
而且,你可以发现,距离越远,宽越大,反之越小
你组成的矩形得是一个合格的矩形吧,意思就是,高是取决于矮柱子的
所以结论就是,每次计算矮柱子的 高 和 底部宽 的乘积就是面积了
所以,你可以想到在从左右两边向中间收缩检查,因为左右最远的时候,宽最大啊
定义左右指针,分别指向左右两边的柱子,计算矮柱子和宽的乘积,与预设最大面积比较,更新最大面积
然后呢?
你想啊,面积取决于矮柱子,那么假如向内移动高柱子,面积是不是要么不变(移动后的柱子还是比矮柱子高),要么变小(移动后的柱子比矮柱子还矮),所以面积一定减小或不变,这怎么能行?
所以你得移动矮柱子,矮柱子向内移动后,要么面积不变(和之前一样高),要么面积变大(比之前高),虽然也可能变小(比之前矮),但是还是有可能变大,所以我们决定移动矮柱子
var maxArea = function(height) {
let i = 0, j = height.length - 1, res = 0;//左右指针,在区间左右两侧
while(i < j) {//老套路
res = height[i] < height[j] ? //比比看,哪个矮
Math.max(res, (j - i) * height[i++]): //左边矮,向右移,计算面积,更新最大值
Math.max(res, (j - i) * height[j--]); //右边矮,向左移,计算面积,更新最大值
}
return res;
};
//上面为了写注释方便,就分层了,大家自己注意把注释移除再试
10.数据流中的中位数(hard)
这个题其实“男”就“男”在计算中位数,因为中位数的计算要看数据整体是奇数个还是偶数个,奇数个,中位数就是最中间那个(也可以是中间那个数再加一遍自己再除2),偶数个,中位数就是最中间的两个的数求和除2,而在这个题中,它要的是目前数据流中的中位数,也就是得实时更新,这才是难点。
这个直接看注释,很好理解
var MedianFinder = function() {
this.queue = [];//定义一个数组,存放数据流
this.left = -1;//左指针,初始指向为-1,表示数组中还没有数据
this.right = -1;//右指针,同上
};
/**
* @param {number} num
* @return {void}
*/
MedianFinder.prototype.addNum = function(num) {
if(this.left === -1){//如果数据流是空的,上面说了-1代表数据流是空的,没数据
//左右指针都向右移动,因为一个元素时中位数就是左右指针对应值的和的二分之一
this.left ++;
this.right ++;
}else{//数据流中已经有了数据,下面是重点✨✨✨✨
//如果左右指针在同一个位置,代表当前数据是奇数个,现在执行到这,数据会变成偶数个
//所以右指针右移一个,这样计算中位数,还是左右指针对应值和的二分之一
if(this.left === this.right){
this.right ++;
}else{//如果当前左右指针位置不同,说明当前数据是偶数个,再加一个就是奇数个了
//左指针右移一个,这样加入一个变成奇数个时,左右指针还是指向同一元素,中位数计算依旧可以
this.left ++;
}
}
this.queue.push(num);
};
/**
* @return {number}
*/
MedianFinder.prototype.findMedian = function() {
if(!this.queue.length) return null;
this.queue.sort((a,b)=>a - b);
//不管是奇数还是偶数个,中位数都可以是相加,除2
return (this.queue[this.left] + this.queue[this.right]) / 2;
};
好了,双指针专题到此告一段落,后续会出难题版本的哈!
加油,力扣人!(此刻2021年11月3日00:00)
看都看到这了,给个一键三连再走呗