LeetCode第283场周赛
文章目录
- 6016. Excel 表中某个范围内的单元格
-
- 题目
- 解题思路:遍历
- 6017. 向数组中追加 K 个整数
-
- 题目
- 解题思路:见缝插针
- 6018. 根据描述创建二叉树
-
- 题目
- 解题思路:双哈希表
- 6019. 替换数组中的非互质数
-
- 题目
- 求最大公约数(Greatest Common Divisor,GCD)
- 求两个数的最小公倍数(Least Common Multiple, LCM)
- 解题思路:栈+模拟
- Reference
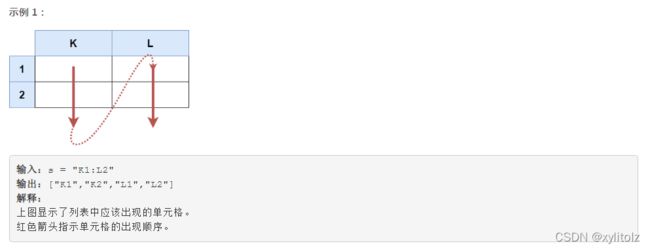
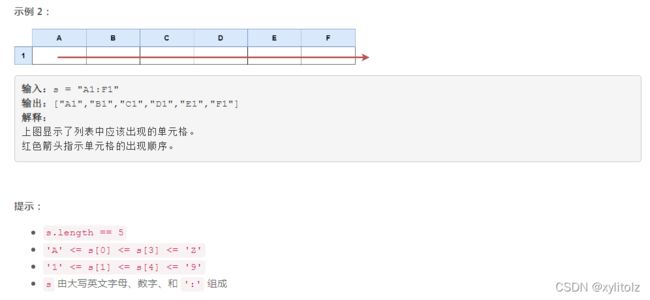
6016. Excel 表中某个范围内的单元格
题目
解题思路:遍历
题目保证s不为空,因此直接可利用索引确定字母和数字的范围,通过双层for循环遍历输出即可。
class Solution {
public List<String> cellsInRange(String s) {
List<String> res = new ArrayList<>();
// 字母维
for (int i = s.charAt(0) - 'A'; i <= s.charAt(3) - 'A'; i++) {
// 数字维
for(int j = s.charAt(1) - '0'; j <= s.charAt(4) - '0'; j++) {
StringBuilder sb = new StringBuilder();
sb.append((char)(i + 'A'));
sb.append(j);
res.add(sb.toString());
}
}
return res;
}
}
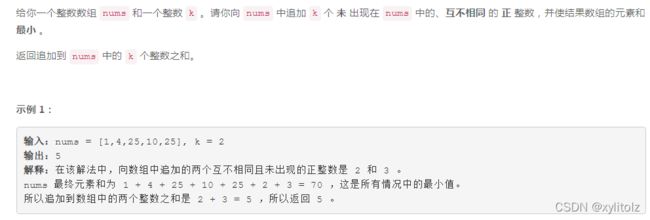
6017. 向数组中追加 K 个整数
题目
解题思路:见缝插针
见缝插针
题目要求插入k个数字后的数组元素和最小且插入的数字在数组中未出现过且互不相同,因此,首先对数组nums进行升序排序,随后从数组左侧开始在数组中进行"见缝插针"式的插入元素,所谓的缝隙即是指:数组中相邻的两个元素的值不连续,例如[1,4]即可以在中间插入2,3这两个元素。
算法流程如下:
- 首先对数组进行升序排列
- 从排序后的首元素开始考虑,若首元素大于1,则可在首元素前插入
nums[0] - 1个元素 - 随后顺序检查排序后的数组中两相邻元素是否连续,若不连续则可插入
nums[i] - nums[i - 1] - 1个元素 - 若数组遍历完成后,插入的元素仍不足
k个,则在数组最后补上[nums[nums.length - 1] + 1, nums[nums.length - 1] + a]剩余的a个元素
在每个缝隙插入元素时,可利用等差数列求和公式 S n = n × ( a 1 + a n ) 2 S_n=\frac{n \times (a_{1} + a_{n})}{2} Sn=2n×(a1+an)以 O ( 1 ) O(1) O(1)时间复杂度计算插入元素之和。
class Solution {
public long minimalKSum(int[] nums, int k) {
// 升序排列,保证插入的元素和最小
Arrays.sort(nums);
// 返回值
long res = 0;
// 要求插入正整数,因此插入的最小值从1开始,单独考虑首元素
if (nums[0] - 1 > 0) {
// 可插入的元素个数
int n = nums[0] - 1;
if (n > k) { // 若可插入的元素个数 > k
// 只插入[1,k]即可
// 等差数列求和公式
res += k * (1L + k) / 2L;
k = 0;
} else { // 若可插入元素个数 < k
// n 个元素全部插入,更新 k 值
k -= n;
res += n * (1L + nums[0] - 1L) / 2L;
}
}
// 顺序检查相邻元素之间是否有缝隙
for (int i = 1; i < nums.length; i++) {
if (k == 0) {
break;
}
if (nums[i] - nums[i - 1] > 1) {
// 可插入的元素个数
int n = nums[i] - nums[i - 1] - 1;
if (n > k) {
res += k * (nums[i - 1] + 1L + nums[i - 1] + k) / 2L;
k = 0;
} else {
k -= n;
res += n * (nums[i - 1] + 1L + nums[i] - 1L) / 2L;
}
}
}
// 插入元素仍不足数
if (k > 0) {
res += k * (nums[nums.length - 1] + 1L + nums[nums.length - 1] + k) / 2L;
}
return res;
}
}
- 时间复杂度: O ( n ) O(n) O(n), n n n为数组 n u m s nums nums的长度
- 空间复杂度: O ( 1 ) O(1) O(1)
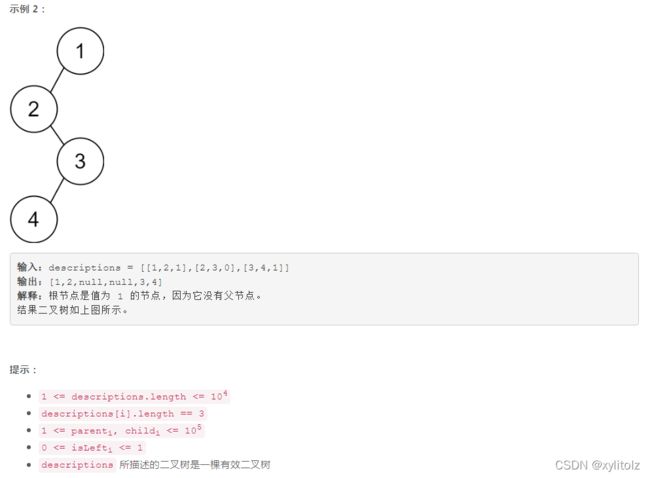
6018. 根据描述创建二叉树
题目
解题思路:双哈希表
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode createBinaryTree(int[][] descriptions) {
// key:非叶子节点值,value:对应的父节点值
// 近存储非叶子节点
HashMap<Integer, Integer> rootMap = new HashMap<>();
// key: 节点值, value:节点地址
// 存储全部节点
HashMap<Integer, TreeNode> map = new HashMap<>();
// 构造出所有节点
for (int[] des : descriptions) {
TreeNode parent, child;
// 判断当前节点是否已经创建
if (map.containsKey(des[0])) {
parent = map.get(des[0]);
} else {
// 创建新节点,并放入map
parent = new TreeNode(des[0]);
map.put(des[0], parent);
}
if (map.containsKey(des[1])) {
child = map.get(des[1]);
} else {
child = new TreeNode(des[1]);
map.put(des[1], child);
}
// 判断属于左子树还是右子树
if (des[2] == 0) {
parent.right = child;
} else {
parent.left = child;
}
// 将非叶子节点的父节点值初始化为 0
if (!rootMap.containsKey(des[0])) {
rootMap.put(des[0], 0);
}
}
// 更新每个节点的父节点
for (int[] des : descriptions) {
if (rootMap.containsKey(des[1])) {
rootMap.put(des[1], des[0]);
}
}
// 遍历 rootMap 寻找根节点
for (int key : rootMap.keySet()) {
// 若某一非叶子节点没有父节点,则就是根节点
if (rootMap.get(key) == 0) {
return map.get(key);
}
}
return null;
}
}
- 时间复杂度: O ( n ) O(n) O(n), n n n代表节点数量
- 空间复杂度: O ( n ) O(n) O(n)
6019. 替换数组中的非互质数
题目
求最大公约数(Greatest Common Divisor,GCD)
- 暴力法
public static int gcd(int a, int b) {
int big = a > b ? a : b;
int small = a < b ? a : b;
if (big%small == 0) {
return small;
}
for (int i = small / 2; i > 1; i--) {
if (small%i == 0 && big%i == 0) {
return i;
}
}
return 1;
}
- 辗转相除法
该方法基于一条定理,两个正整数a,b(a>b),它们的最大公约数等于a除以b的余数c和b之间的最大公约数。例如:10和25,25除以10商2余5,那么10和25的最大公约数等同于10和5的最大公约数。
public static int gcd(int a, int b) {
return b == 0 ? a : gcd2(b, a % b);
}
public static int gcd(int a,int b){
int big = a>b?a:b;
int small = a<b?a:b;
if(big%small == 0){
return small;
}
return gcd(big%small,small);
}
求两个数的最小公倍数(Least Common Multiple, LCM)
最小公倍数(Least Common Multiple,LCM),如果有一个自然数a能被自然数b整除,则称a为b的倍数,b为a的约数,对于两个整数来说,指该两数共有倍数中最小的一个。计算最小公倍数时,通常会借助最大公约数来辅助计算。
- 相乘法
如果两个数是互质数,那么它们的最小公倍数就是这两个数的乘积。
例如4和7是互质数,所以它们的最小公倍数就是 4 × 7 = 28 4 \times 7 = 28 4×7=28
- 直接法
如果两个数是倍数关系,那么较大的数就是这两个数的最小公倍数。
例如15是3的倍数,所以它们的最小公倍数就是较大的数15
- 扩倍法
如果两个数不是互质,也没有倍数关系时,可以把较大的数依次扩大2倍、3倍、4倍、…直到所得的结果是较小数的倍数时,这个数就是这两个数的最小公倍数。
例如:求18和30的最小公倍数
30 × 2 = 60 30 \times 2 = 60 30×2=60,60不是18的倍数
30 × 3 = 90 30 \times 3 = 90 30×3=90,90是18的倍数,因此18和30的最小公倍数就是90
- 约分法
此方法较复杂,但使用范围广,因为两个数的乘积等于这两个数的最大公因数和最小公倍数的乘积
例如:求18和30的最小公倍数
18和30的最大公因数为6
18 ÷ 6 = 3 , 3 × 30 = 90 18 \div 6=3,3 \times 30 = 90 18÷6=3,3×30=90
或者
30 ÷ 6 = 5 , 5 × 18 = 90 30 \div 6 = 5, 5 \times 18 = 90 30÷6=5,5×18=90
所以18和30的最小公倍数就是90
- 分解法
先把要求的两个数分别分解质因数,然后再把它们公有的质因数和各自独有的质因数连乘起来,所得的积就是它们的最小公倍数
例如:求12和18的最小公倍数
12 = 2 × 2 × 3 12=2 \times 2 \times 3 12=2×2×3, 18 = 2 × 3 × 3 18=2 \times 3 \times 3 18=2×3×3
它们公有的质因数是2和3,独有的质因数是2和3
所以12和18的最小公倍数为 2 × 3 × 2 × 3 = 36 2\times 3 \times 2 \times 3 =36 2×3×2×3=36
- 借助最大公约数
最 小 公 倍 数 = 两 数 的 乘 积 最 大 公 约 数 最小公倍数=\frac{两数的乘积}{最大公约数} 最小公倍数=最大公约数两数的乘积
public static int LCM(int a, int b) {
int big = a > b ? a : b;
int small = a < b ? a : b;
// 扩倍法
int i = 1;
int res = 0;
while(true) {
int product = big * i;
if (product%big == 0 && product%small == 0) {
res = product;
break;
}
i++;
}
return res;
}
解题思路:栈+模拟
算法流程如下:
- 创建一个栈,栈中初始元素为 n u m s [ 0 ] nums[0] nums[0]
- 从 n u m s [ 1 ] nums[1] nums[1]开始遍历数组:
- n u m s [ i ] , 1 ≤ i ≤ n − 1 nums[i], 1 \le i \le n-1 nums[i],1≤i≤n−1入栈,循环,从栈顶取出两个元素
- 若其互质,则退出循环
- 否则将这两个元素的最小公倍数入栈,循环直至栈内只有一个元素为止
- n u m s [ i ] , 1 ≤ i ≤ n − 1 nums[i], 1 \le i \le n-1 nums[i],1≤i≤n−1入栈,循环,从栈顶取出两个元素
- 遍历 nums \textit{nums} nums 结束后的栈就是答案
class Solution {
public List<Integer> replaceNonCoprimes(int[] nums) {
List<Integer> res = new ArrayList<>();
res.add(nums[0]);
for (int i = 1; i < nums.length; i++) {
res.add(nums[i]);
while (res.size() > 1) {
// 使用ArrayList模拟栈
int x = res.get(res.size() - 1); // 栈顶元素
int y = res.get(res.size() - 2); // 次栈顶元素
int g = gcd(x, y);
if (g == 1) {
break;
}
// 删除这两个数,并 替换 为它们的 最小公倍数
// 移除栈顶和次栈顶元素
res.remove(res.size() - 1);
res.remove(res.size() - 1);
// 替换 为它们的 最小公倍数 = x * y / 最大公约数
// x*y/g 换成 x/g*y 就不需要强制类型转化了
res.add(x / g * y);
}
}
return res;
}
// 求最大公约数
private int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
}
Reference
- 求两个数最小公倍数
- C语言求最小公倍数(详解版)
- 求最大公约数
- 利用栈模拟