动态规划——背包问题

背包问题

总共有N个物品，背包容量为V，每个物品的体积为v[i]，价值为w[i]

1. 0-1背包问题

使用滚动数据优化存储空间，将记录表优化成一维：

N,V = map(int, input().strip().split())

v, w = [0]*(N+1), [0]*(N+1)

f = [0]*(V+1)

for i in range(1,N+1):
    v[i], w[i] = map(int, input().strip().split())

for i in range(1, N+1):
    for j in range(V, v[i]-1, -1):
        f[j] = max(f[j], f[j-v[i]]+w[i])

print(f[V])

2. 完全背包问题

原本需要使用三层循环，内层遍历k计算最终的答案，但是通过观察f[i][j-v]与f[i][j]的关系，我们发现可以通过f[i,j-v]+w来获得f[i,j]，于是优化为二层循环。

N, V = map(int, input().strip().split())

v = [0] * (N+1)
w = [0] * (N+1)

f = [0]*(V+1)

for i in range(1, N+1):
    v[i], w[i] = map(int, input().strip().split())

for i in range(1, N+1):
    for j in range(v[i], V+1):
        f[j] = max(f[j], f[j-v[i]]+w[i])


print(f[V])

3. 多重背包问题

最基础的方法（不带任何优化）

N,V = map(int, input().strip().split())

s,v,w = [0]*(N+1), [0]*(N+1), [0]*(N+1)

f = [[0]*(V+1) for i in range(N+1)]

for i in range(1, N+1):
    v[i], w[i], s[i] = map(int, input().strip().split())

for i in range(1, N+1):
    for j in range(1, V+1):
        for k in range(0, s[i]+1):
            if j >= k*v[i]:
                f[i][j] = max(f[i][j], f[i-1][j-v[i]*k]+w[i]*k)
            else:
                break

print(f[N][V])

使用二进制存储优化：

N,V = map(int, input().strip().split())

s,v,w = [0]*25000, [0]*25000, [0]*25000

f = [0] * 25000

cnt = 0
for i in range(1, N+1):
    vi, wi, si = map(int, input().strip().split())
    k = 1
    while k <= si:
        cnt += 1
        si -= k
        v[cnt] = vi*k
        w[cnt] = wi*k
        k *= 2
    if si>0:
        cnt += 1
        v[cnt] = si*vi
        w[cnt] = si*wi

N = cnt
for i in range(1, N+1):
    for j in range(V, v[i]-1, -1):
        f[j] = max(f[j], f[j-v[i]]+w[i])
print(f[V])

4. 分组背包问题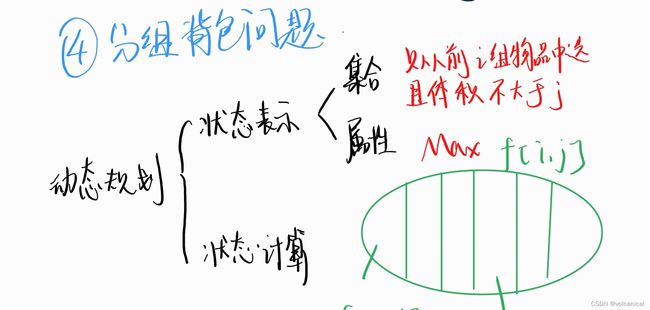

# 有N组 背包容量为V
N,V = map(int, input().strip().split())

v, w, s = [[0]*200 for i in range(200)], [[0]*200 for i in range(200)], [0]*200

f = [0] * 200

for i in range(1, N+1):
    s[i] = int(input())
    for j in range(s[i]):
        v[i][j], w[i][j] = map(int, input().strip().split())

for i in range(1, N+1):
    for j in range(V, -1, -1):
        for k in range(s[i]):
            if v[i][k] <= j:
                f[j] = max(f[j], f[j-v[i][k]]+w[i][k])
                
print(f[V])