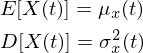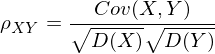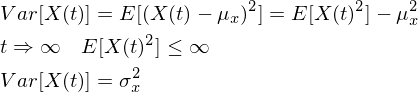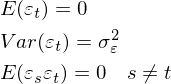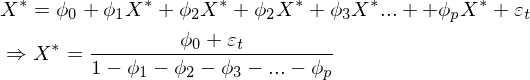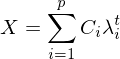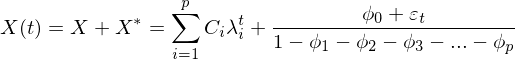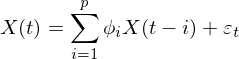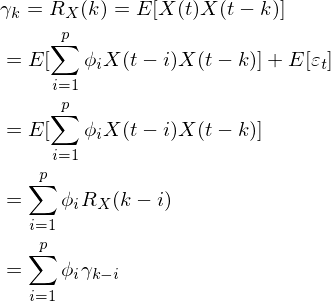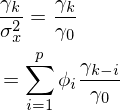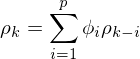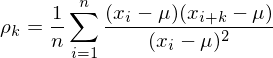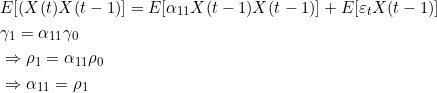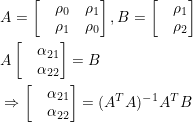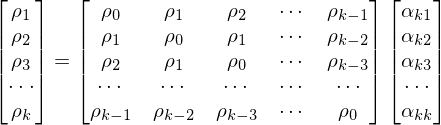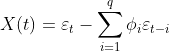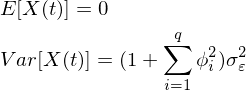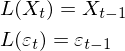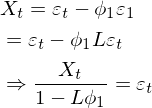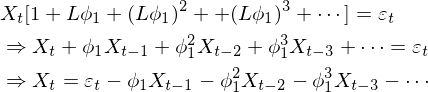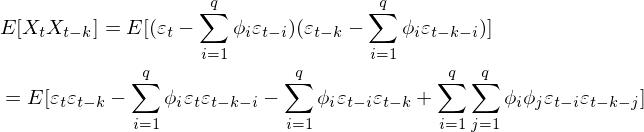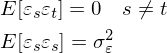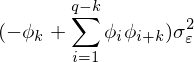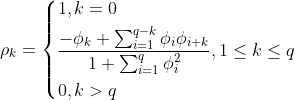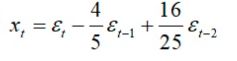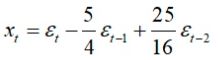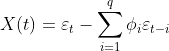时间序列分析:AR(p),MA(q)
在一个连续的时间周期内随机变量发生变化,比如一个月内股票价格走势、每年的销售额、每小时进出园区的车辆等,这些都称为时间序列。时间序列分析通过分析过去一段时间内随机变量的走势,预测未来随机变量走势,时间分析对数据是有要求的,首先需要时间序列本身是平稳的,在满足平稳性后还需检查是否为白噪音:白噪音数据在时间维度上没有关联性。所有条件都满足后,常用的时序分析模型有AR(p)、MA(q)、ARMA等,也可以使用循环神经网络如lstm等完成时序模型的训练。
一、随机过程及其数学特征
1.1 数学期望函数、方差函数
经典概率论与随机过程最大区别在于随机过程具有时序性,经典统计学通常的场景是:从总体中随机抽取一个样本,这个样本的分布称为抽样分布,从抽样分布中构造完全统计量并分析该统计量的分布,常见统计量有均值、方差、偏度、峰度等。比如为了统计零件的尺寸,从仓库中(总体)中抽取100个零件构成样本,计算100个零件平均值
![]()
作为对零件总体一个评估,测量这个样本中的每个零件的顺序对于结果没有差异,经典概率论中将频率汇总成概率分布形式,汇总一词指出了对于顺序没有要求。如果有多个样本即分多次抽取、每次抽取100个零件,计算每批零件(样本)的均值是不一样的,统计量的分布与随机变量分布存在着关系,零件的尺寸是一个随机变量,假设该变量服从正态分布N(μ,σ2),那么平均值也服从正态分布N(μ,σ2/100),的数学期望与零件尺寸一样但是方差更小,所以更为接近总体尺寸实际期望值。
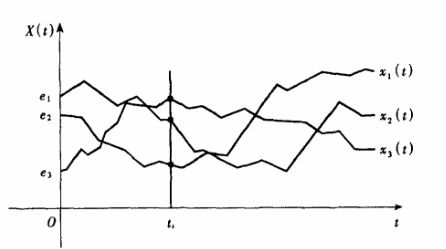
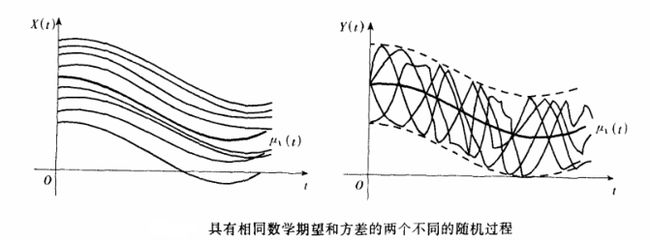
随机过程例子是股票指数,以30天为一个周期统计大盘每天的指数,用x1(t)代表这30个序列,x1(t)称为样本函数,类似还可以取一年当中其他30天依次得到x2(t)、x3(t)、x4(t)、x5(t)...等,集合{x1(t)、x2(t)、x3(t)、x4(t)、x5(t)...}称为随机过程,随机过程通常用大写X(t)表示,随机过程的所有样本函数绘在一个坐标系内如下图所示:
任取一个时间点t1,可以得到一个截面,各个样本函数在时间点t1具有不同值,在这个'截面'上不同的值有不同的概率分布、概率密度函数、方差等,不同的时间点(截面)固定了随机过程时间维度,从而转为传统的静态的概率统计分析:
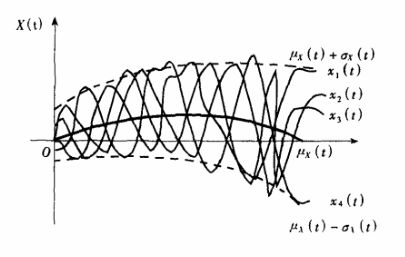
一般来说,随机过程在不同时间点的数学期望和方差是不一样的,其数学期望或方差都是时间的函数,设随机过程的数学期望函数为
![]()
,方差函数为,具体公式如下:
随机过程的各个样本函数x1(t)、x2(t)、x3(t)、x4(t)、x5(t)...xn(t)会始终围绕
![]()
且波动范围是:
1.2 自相关函数与平稳随机过程
在概率统计中使用协方差来比较两个随机变量的线性相关性:
![]()
进一步的,为了取消纲量的影响,用协方差除以两个随机变量的标准差得到协方差系数,协方差系数ρxy是一个绝对值小于1的实数:
ρxy=0时说明随机变量X,Y没有线性相关性,ρxy接近1时两者有较强正线性相关性,ρxy接近-1时两者有较强负线性相关性,需要强调的是,协方差系数ρxy等于0只能说明两个随机变量没有线性相关性,并不代表X、Y没有诸如
![]()
这样的非线性相关性。随机过程也有类似协方差的概念,由于随机过程各个样本函数都源自同一个随机变量,所谓的相关性都是与自身比较,在任意两个时刻t1、t2,随机过程的自相关函数定义为:
![]()
(1.1)
自相关函数反映时间序列在不同时刻的关联性,下图两个不同时间序列其数学期望函数、方差函数一样,但前者的自相关系数大于后者从而也显示出一定规律性,随着时间的延迟后者不同时刻的值变得毫无规律可循,一个平稳随机过程的自相关系数较低很有可能是白噪音,无法使用时序模型分析白噪音:
在公式(1.1)中,如果随机过程X(t)是连续的,且t1=t2-τ(τ为常数),自相关函数等效于下面的积分形式:
从上式可以看出,自相关函数本质是卷积,从信号学知道时域的卷积函数经过傅里叶变换后,变为频域的乘积,自相关函数经过傅里叶变换后也叫时间序列(信号)的功率谱,自相关函数的物理意义是:时间序列每个时刻的值可以用频率来描述,自相关函数反映出两个时刻频率相关联的系数,如果时间序列有较强自相关性,就可用一些常见模型或数学公式来表达它。关于信号的相关性再举一个事例,近期有报道称,俄罗斯在千叶群岛精确的定位了一艘美国的“弗吉尼亚”级核潜艇,俄罗斯事先掌握了美国多个核潜艇对应的声噪样本,在实战中俄罗斯用检测到声噪与现有样本逐一比较相关性,当有明显相关数值出现时即可锁定该潜艇,这个事例运用了不同信号间的互相关性。自相关函数是任意两个时刻t1、t2混合原点矩的数学期望,而t1、t2两个时刻的混合中心矩称为协方差函数:
![]()
(1.2)
自相关函数与协方差函数有着对应关系:
![]()
(1.3)
在平稳随机过程中,有性质
![]()
,同时把随机过程所有的样本函数向下平移μ个单位后(去中心化),新的随机过程,根据公式1.3此时自相关函数与协方差函数相等,利用去中心化可以简化时序模型的推导并且不会影响模型本身的性质。自相关函数、协方差函数带有纲量,按以往经验除以标准差可以得到相应系数,如自相关系数定义为:
(1.4)
随机过程离散化表示方式是{X(t),t∈T},T=0,±1,±2,±3,±4,...,如果随机过程{X(t),t∈T}满足以下三个条件:
1、
![]()
数学期望函数是常数
2、
![]()
自相关函数仅与间隔k有关,与时刻t无关
3、
![]()
原点二阶矩存在
则称该随机过程为宽平稳随机过程、或者叫广义随机过程等。条件3说明随机过程的标准差在t趋近
![]()
时等于常数σx:
数学上定义的平稳随机过程要求很严格,通常情况下,随机过程难以满足其定义的,但在工程应用上,只要满足以上三个较为宽松条件就认为是平稳随机过程。条件1和3约束了时间序列只能在一个固定轴上上下有限波动,比如超出数学期望时会下降而低于数学期望时会上升,这是一种平均回归现象;条件2自相关函数仅与间隔k有关,确保了在具体间隔,时间序列的自相关性是一个常数(自相关函数代入具体的k得到一个常数),这说明时间序列在规定间隔内有稳定的相关性,这些条件都在为接下来使用AR、MA、ARMA、ARIMA模型做运算上铺垫。时间序列分析首先要检查是否为平稳随机过程,如果为非平稳随机过程则失去进一步分析意义,当随机过程为非平稳过程时,可以通过一阶差分、二阶差分操作生成新的序列,直到序列为平稳过程为止,一阶差分生成过程为:
![]()
二、AR(p)、MA(q)模型
2.1 AR(p)平稳性判断、自相关系数、偏相关系数
AR(p)模型表达式为:
![]()
(2.1)
(2.1)表明Xt与前面p项随机变量有关,εt表示数学期望为0、标准差为σε随机误差,且任意两个时刻的误差相互独立:
当随机过程X(t)用AR(p)模型表达时,并不能代表这个随机过程为平稳随机过程,(2.1)是一个差分方程,方程的解Xt是自变量为t的一元高次代数式,而当这个随机过程是平稳随机过程时,方程的解一定是收敛的,即(2.1)有稳定解,设稳定解为X*,当t趋近
![]()
时,有X*≈Xt≈Xt-1≈Xt-2≈Xt-3≈Xt-4≈...Xt-p,将X*代入到2.1式中有:
稳定解X*构成包含了随机过程的数学期望,之前介绍过平稳随机过程的数学期望函数是一个常数,设该随机过程数学期望为μ,对(2.1)等式两边取数学期望运算:
(2.1.1)
稳定解X*可以表达成随机过程数学期望与一个随机误差之和:
(2.2)
(2.2)式表明如果一个形如AR(p)的随机过程为平稳随机过程,那么其稳定后时间序列将围绕常数μ上下有限波动,到目前为止所有的结论都是基于假设该随机过程为平稳随机过程, AR(p)表达式为线性差分方程,线性差分方程的解等于通解加上特解,特解是一个常数,不妨就把稳定解X*作为特解,而(2.1)的通解是下面线性齐次方程的解。
![]()
(2.3)
设
![]()
,上式可写为:
![]()
即线性齐次差分方程(2.3)特征方程为:
![]()
(2.4)
该方程有p个根:λ1,λ2,λ3,λ4,...λp,这p个根可能各不相等,也有可能有部分重根,也有可能是虚数根,以p个不同实数根为例,此时方程的(2.3)的解是:
(Ci为常数)
即方程(2.1)的解是:
(2.5)
如果随机过程是平稳随机过程则X(t)必须在t趋近
![]()
时等于稳定解X*,就要求方程(2.4)所有的根模小于1,即|λi|<1,这就是判断随机过程是否为平稳随机过程的条件,也称单位根检验。从(2.5)式可以看出:虽然AR(p)表示的是各个时刻随机变量的线性关系,但本质上是利用一元高次曲线来拟合时间序列的走势。
如果随机过程经过单位根检验,可确定为平稳随机过程,接下来还需要排除为白噪音。前面介绍过,有的白噪音也是平稳随机过程,通过自相关系数可以区分出白噪音。介绍AR(p)的自相关系数之前,为了运算方便先对AR(p)表达式做个简单变形,(2.1)式右边减去ψ0得到新时间序列:
(2.6)
新的时间序列只是原时间序列平移了ψ0个单位,此为去中心化操作,新的时间序列保留了原序列相关性,新的时间序列ψ0=0,代入公式2.1.1可知:E[X(t)]=0,方差也和原序列一致。接下来利用去中心化后形式(2.6)讨论AR(p)自相关系数,以及由自相关系数引出偏自相关系数,有自相关函数定义知,(2.6)式两边同乘以Xt-k并取数学期望得到k阶自相关函数:Rx(t,t-k)=Rx(k):
(2.6.1)
自相关函数除以方差得到自相关系数(acf),由于已经去中心化,有
![]()
:
设k阶自相关系数为ρk:
(2.7)
由于平稳过程自相关函数仅与时间间隔相关,自相关函数有对称性即:R(t+k,t )=R(t,t+k)=R(t-k,t ),R(k)=R(-k),相应的,自相关系数也有对称性:
从(2.6.1)自相关函数推导过程可以看出,任意阶自相关函数都有意义的,随着k增大自相关函数逐渐趋近0,所以AR(p)的自相关系数呈现出一定'拖尾',有时候自相关系数在正负值之间交替,系数值逐渐趋近于0也算是'拖尾'性。实际应用中通过下面的公式得到自相关系数的估计值:
(2.8)
公式(2.8)对应于协方差系数公式,也可以看成去中心化后自相关系数,下面的代码利用(2.8)实现时间序列的自相关系数计算:
import numpy as np
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.stattools import acf,pacf
def generateerr(fn=np.random.randn):
err = fn(1, 1)[0, 0]
return err
def genardata(num):
y=[]
y.append(0)
#y.append(0)
for i in range(num):
err=generateerr()
y.append( y[-1]*0.65 +err)
return np.array(y)
#计算自相关系数
def acfvalues(TimeSeries):
Xt,Xt_k,AutoCovariance = [],[],[]
avg = np.mean(TimeSeries)
i = 1
while i < len(TimeSeries):
t,t_k = TimeSeries[i::],TimeSeries[:-i:]
Xt.append(t)
Xt_k.append(t_k)
i += 1
k = 0
result_temp0 = 0
# 首先求γ0的值
while k < len(TimeSeries):
result_temp0 = result_temp0 + pow((TimeSeries[k] - avg), 2)
k += 1
AutoCovariance.append(result_temp0 / len(TimeSeries))
# 然后计算分子
p = 0
q = 0
while p < len(Xt):
q = 0
result_temp1 = 0
while q < len(Xt[p]):
result_temp1 = result_temp1 + (Xt[p][q] - avg) * (Xt_k[p][q] - avg)
q += 1
AutoCovariance.append(result_temp1 / len(TimeSeries))
p += 1
#以上为自相关函数计算过程,除以γ0得到自相关系数
pks = [ t/AutoCovariance[0] for t in AutoCovariance]
return pks
if __name__=='__main__':
N=1000
y=genardata(N)
# 是否为非平稳序列
pvalues = adfuller(y)
print('平稳随机过程判断:')
print(pvalues)
# 是否为白噪音
pvalues = acorr_ljungbox(y, lags=[1, 2, 3, 4, 5 ])
print('白噪音判断:')
print(pvalues)
print('实现自相关系数计算:')
print(acfvalues(y)[0:10])
acfs_stattools = acf(y,nlags=10 )
print('自相关系数(stattools):')
print(acfs_stattools[:])
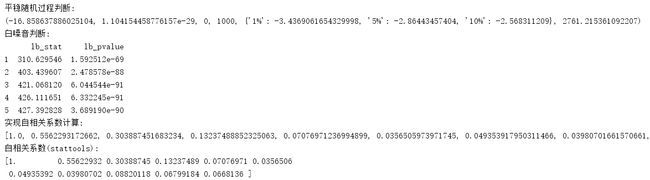
程序先利用p值检验是否为平稳随机过程(零假设为非平稳过程);随后检查是否为白噪音(零假设为是白噪音),当两者p值很小接近0时,可认为该时间序列非白噪音的平稳随机过程。利用公式(2.8)实现自相关系数的计算,另外利用用stattools提供的算法做对比,计算结果如下:
时间序列另外一个重要的统计量是偏自相关系数(pacf),偏自相关系数可以从自相关系数导出。从(2.6)式AR(p)公式可以看出,选定一个滞后期k(k α11为1阶偏自相关系数,上式两边同乘以X(t-1)取数学期望,并除以方差后得: 很明显,1阶自相关系数与1阶偏自相关系数相等,设有p=3的AR(3)模型,计算k=2阶偏自相关系数: 这时可以认为Xt仅与Xt-1,Xt-2存在线性关系,而去除去Xt-3对Xt的影响,写成表达式: 上式中α22为2阶偏自相关系数,注意,上式中的α21并不是1阶偏自相关系数,因为此时的X(t-1)并没有除去X(t-2)对系数的影响,α21只是一个临时变量。上式两边同乘以X(t-1)、取数学期望、除以方差后得到: 同样两边同乘以X(t-2)、取数学期望、除以方差后得到另一组等式: 上面两个等式中,自相关系数ρ0、ρ1、ρ2已知,解方程组可得2阶偏自相关系数α22,写成线性代数形式为: 解方程组,设: 特殊的当k=p时,p阶偏自相关系数为公式(2.6)中的 ;当k (2.9) 解方程组其中αkk为k阶偏自相关系数,(2.9)方程组也叫尤尔—沃克方程(Yule-Walker)。对于AR(p)结构的时间序列,X(t)仅与X(t-1),X(t-2)...X(t-p)p个时刻相关,即当k>p时偏自相关系数趋近0,这说明AR(p)偏自相关系数具有截尾性,通过自相关系数拖尾、偏相关系数截尾即可判断时间序列适用于AR(p)模型。另外,利用Yule-Walker方程不仅可以得到AR(p)模型的偏系相关系数,还可以求出MA(q)模型的偏系相关系数。 2.2 MA(q)统计数学特征 MA(q)的表达形式为: 与AR(p)一样,MA(q)去中心化后形式并不影响关联性,令μ0=0有去中心化后形式: (2.2.1) MA(q)数学期望函数、方差函数: 由于MA(q)数学期望函数、方差函数都是常数,一般情况认为MA(q)的天生的平稳性,需要考虑的MA(q)与AR(p)之间相互转换的性质。介绍MA(q)特性前首先引入滞后算子的概念,滞后算子L具有以下特性: 滞后算子L可通过当期值得到上期值,滞后算子可以迭代使用: ,。所谓算子就是将一个函数变为另一个函数,随机过程X(t)从图像上来看是一个自变量为t的连续函数,也可以理解为一个信号,不妨设这个函数为f(t),而滞后算子L本质是拉普拉斯变换,通过拉普拉斯变换可将一个实变函数变换为复变函数、将时域的信号变为'复频域'的信号,公式如下: 上式中s是一个复数,拉普拉斯变换表达的频率更丰富,其变换后频率是复数:复频域,复数的频率可以表示一个逐渐衰减的信号,傅里叶变是拉普拉斯变换一种特殊形式。拉普拉斯变换也有逆变换,即将复频域信号还原到时域信号,同时拉普拉斯变换有位移性: 总之通过拉普拉斯变换、位移、逆变换等操作可以得到时间序列上一期的值,这一系列操作用L表示。利用滞后算子来分解MA(1)结构: 当 时,上式可以写为幂级数形式: (2.2.2) MA(1)可以表示成AR(p)无穷级数的形式,MA(q)用归纳法可以得到相同的结论,利用Yule-Walker方程组解MA偏自相关系数可以到无穷阶,所以MA(q)的偏自相关系数呈现出拖尾性,根据公式1.1MA(q)k阶自相关函数定义为: 由独立性存在: k=0时,k阶自相关函数等于 。 a) 1<=k<=q 时,k阶自相关函数等于 b) k>q时,k阶自相关函数等于0。 c) 自相关函数除以方差得到MA(q)的k阶自相关系数公式: (2.2.3) k>q时相关系数等于0说明MA(q)自相关系数具有q阶截尾性,观察(2.2.3)可以发现当q>=2时,给定一个自相关系数ρk,可通过一组q元q次方程组求解参数 ,方程有多个根,也就是说对于同一个自相关系数有多个不同MA(q)模型与之对应,如下面两个MA(2)模型: 这两个模型的自相关系数相同: 如为了能让自相关系数与唯一的MA(q)模型对应,就需要添加额外条件去除其他结构的MA(q)实例,这种唯一性的对应称为MA(q)的可逆性,前面说过对于MA(q)一般不检查平稳性(天然性满足),取而代之的是要事先检查可逆性。满足可逆性的MA(q)转化为AR(p)形式后是收敛的,以2.2.1去中心化后MA(q)为例: X(t)在t趋近于 后收敛于0,上式右边为差分方程,可设通解,得到特征方程: (2.2.4) 解此齐次方程可得到p个不同根或s个重根,根为实数或虚数,当所有根|λi|<1时,即所有根都在单位圆内时,εt收敛同时X(t)也收敛。概括来说,当MA(q)的特征方程(2.2.4)所有的根都在单位圆内时,该MA(q)具有可逆性,并且这样的MA(q)模型与自相关系数一一对应。 三、通过自相关系数,偏相关系数求解AR(p)、MA(q)参数 根据现有的时间序列,利用(2.8):自相关系数估计公式,以及(2.9):Yule-Walker方程得到AR(p)和MA(q)的自相关系数和偏自相关系数,利用不同模型拖尾、截尾性可判断出时间序列适用于哪种模型,进一步,通过截尾性可以确定p或q的值: 接下来利用时间序列、自相关系数、偏自相关系数求解出模型中参数: 以及随机波动ξt(的方差,接下来分别用回归和牛顿迭代法(newton-raphson)求解,并用python代码实现这两种过程。 以下内容请转至链接:时间序列分析![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()