5.3 标准化数据

5.3.1 离差标准化

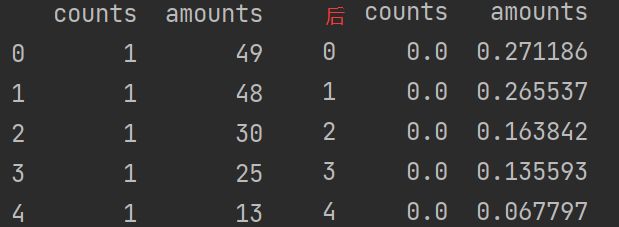
  离差标准化是对原始数据的一种线性变换，结果是将原始数据的数值映射到[0,1]区间之间，转换公式为

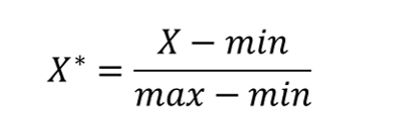
  其中max为样本数据的最大值，min为样本数据的最小值，max-min为极差。离差标准化保留了原始数据值之间的联系，是消除量纲和数据取值范围影响最简单的方法。

import pandas as pd
detail = pd.read_csv('F:/书籍/Python数据分析与应用/
37304_Python数据分析与应用_源代码和实验数据/第5章/data/detail.csv',
                     encoding='gbk')
# print(detail)
# 自定义离差标准化函数
def MinMaxScale(data):
    data = (data - data.min()) / (data.max() - data.min())
    return data

# 对菜单订单表售价和销量做离差标准化
d1 = MinMaxScale(detail['counts'])
d2 = MinMaxScale(detail['amounts'])
d3 = pd.concat([d1, d2], axis=1)
print(detail[['counts', 'amounts']].head())
print(d3.head())

  从运行结果可以发现，数据的整体分布情况并不会随离差标准化而发生改变，原先取值较大的数据，在做完离差标准化后的值依旧较大。
  当数据和最小值相等的时候，通过离差标准化可以发现数据变为0。
  若数据极差过大就会出现数据在离差标准化后数据之间的差值非常小的情况。
  同时，还可以看出离差标准化的缺点：若数据集中某个数值很大，则离差标准化的值就会接近于0，并且相互之间差别不大。

5.3.2 标准差标准化数据

  标准差标准化也叫零均值标准化或分数标准化,是当前使用最广泛的数据标准化方法。经过该方法处理的数据均值为0 ,标准差为1 ,转化公式如下。

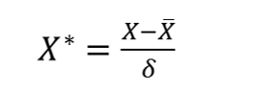
  其中为原始数据的均值，δ为原始数据的标准差。

import pandas as pd
import numpy as np
detail = pd.read_csv('F:/书籍/Python数据分析与应用/'
                     '37304_Python数据分析与应用_源代码和实验数据/第5章/data/detail.csv',
                     encoding='gbk')
# print(detail)
# 自定义标准差标准化函数
def StandaScale(data):
    data = (data - data.mean()) / data.std()
    return data
# 对菜单订单表售价和销量做标准差标准化
d1 = StandaScale(detail['counts'])
d2 = StandaScale(detail['amounts'])
d3 = pd.concat([d1, d2], axis=1)
print(detail[['counts', 'amounts']].head())
print(d3.head())

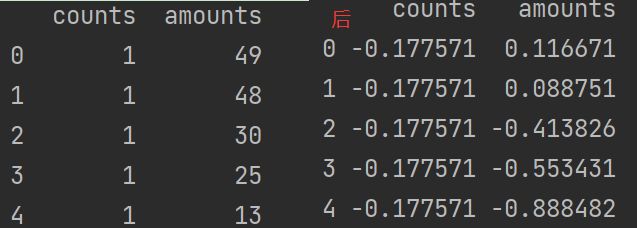
  通过结果发现，标准差标准化后的值区间不局限于[0,1] ,并且存在负值。
  同时也不难发现,标准差标准化和离差标准化一样不会改变数据的分布情况。

5.3.3 小数定标标准化数据

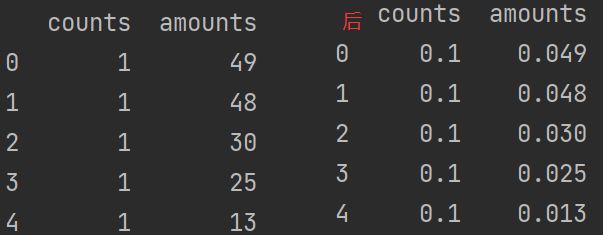
  通过移动数据的小数位数,将数据映射到区间[-1,1]之间,移动的小数位数取决于数据绝对值的最大值。转化公式如下：

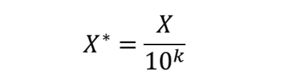
import pandas as pd
import numpy as np
detail = pd.read_csv('F:/书籍/Python数据分析与应用/'
                     '37304_Python数据分析与应用_源代码和实验数据/第5章/data/detail.csv',
                     encoding='gbk')
# print(detail)
# 自定义小数定标标准化函数
def DecimalScale(data):
    data = data / 10**np.ceil(np.log10(data.abs().max()))
    return data
# 对菜单订单表售价和销量做标准差标准化
d1 = DecimalScale(detail['counts'])
d2 = DecimalScale(detail['amounts'])
d3 = pd.concat([d1, d2], axis=1)
print(detail[['counts', 'amounts']].head())
print(d3.head())

总之,三种标准化方法各有其优势:
➢离差标准化方法简单,便于理解,标准化后的数据限定在[0, 1]区间内。
➢标准差标准化受到数据分布的影响较小。
➢小数定标标准化方法的适用范围广,并且受到数据分布的影响较小,相比较于前两种方法而言该方法适用程度适中。