【线性回归、岭回归、Lasso回归分别预测患者糖尿病病情】数据挖掘实验一
Ⅰ、项目任务要求
- 任务描述:将“diabetes”糖尿病患者数据集划分为训练集和测试集,利用训练集分别结合线性回归、岭回归、Lasso回归建立预测模型,再利用测试集来预测糖尿病患者病情并验证预测模型的拟合能力。
- 具体任务要求如下:
- 搜集并加载“diabetes”患者糖尿病指数数据集。
- 定义训练集和测试集(训练集和测试集比例分别为8:2;7:3;6:4)。
- 建立线性回归模型。
- 分别利用可视化方法和交叉验证法确定惩罚参数λ并建立岭回归模型。
- 分别利用可视化方法和交叉验证法确定惩罚参数λ并建立Lasso回归模型。
- 分别用岭回归模型和Lasso回归模型通过测试集预测患者糖尿病病情。
- 利用最小平均均方误差来评估上述三个预测模型的拟合能力。
- 结果分析(上述三种预测模型的对比分析),建议图表结合说明并写出预测模型方程。
参考资料网址:
- 机器学习总结(一):线性回归、岭回归、Lasso回归
- 吴裕雄 数据挖掘与分析案例实战(7)——岭回归与LASSO回归模型
- Python数据挖掘课程 五.线性回归知识及预测糖尿病实例
- 数据挖掘-diabetes数据集分析-糖尿病病情预测_线性回归_最小平方回归
- 用岭回归和LASSO糖尿病治疗效果好坏
II、数据集描述(10)
。。。。。。(详细描述数据集:如特征属性名称及意义、记录数等)
III、主要算法原理及模型评价方法陈述(15分)
。。。。。。(写出项目中涉及的主要算法原理及模型评价方法)
IV、代码实现(45分)
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, model_selection
# from sklearn import datasets, linear_model, discriminant_analysis, model_selection
# todo: 查看数据(训练集:X_train, y_train; 测试集X_test, y_test)
def check_data():
with open("data/X_train.txt", "w") as file:
for i in range(len(X_train)):
file.write(f"【样本{i+1}】:{X_train[i]}\n")
with open("data/y_train.txt", "w") as file:
for i in range(len(y_train)):
file.write(f"【样本{i+1}】:{y_train[i]}\n")
with open("data/X_test.txt", "w") as file:
for i in range(len(X_test)):
file.write(f"【样本{i+1}】:{X_test[i]}\n")
with open("data/y_test.txt", "w") as file:
for i in range(len(y_test)):
file.write(f"【样本{i+1}】:{y_test[i]}\n")
# todo: 可视化展示
def show_plot(alphas, scores):
figure = plt.figure()
ax = figure.add_subplot(1, 1, 1)
ax.plot(alphas, scores)
ax.set_xlabel(r"$\alpha$")
ax.set_ylabel(r"score")
ax.set_xscale("log")
ax.set_title("Ridge")
plt.show()
# Todo: 加载数据
# 加载糖尿病数据集
diabetes = datasets.load_diabetes()
# 使用 model_selection.train_test_split() 将数据集分成训练集和测试集,其中训练集占 75%,测试集占 25%(最佳)
# random_state 参数设置了随机种子,以确保结果的可重复性
X_train, X_test, y_train, y_test = model_selection.train_test_split(diabetes.data, diabetes.target, test_size=0.25, random_state=0)
# 查看划分数据(保存至data/*)
check_data()
# Todo: 建立线性回归模型
print('========== ※ 线性回归模型 ※ ==========')
# 通过sklearn的 linear_model 创建线性回归对象
linearRegression = linear_model.LinearRegression()
# 进行训练
linearRegression.fit(X_train, y_train)
# 通过LinearRegression的coef_属性获得权重向量,intercept_获得b的值
print("权重向量:%s, b的值为:%.2f" % (linearRegression.coef_, linearRegression.intercept_))
# 计算出损失函数的值
print("损失函数的值: %.2f" % np.mean((linearRegression.predict(X_test) - y_test) ** 2))
# 计算预测性能得分
print("预测性能得分: %.2f" % linearRegression.score(X_test, y_test))
# Todo: 分别利用可视化方法和交叉验证法确定惩罚参数λ并建立岭回归模型
print('========== ※ 岭回归模型 ※ ==========')
ridgeRegression = linear_model.Ridge()
ridgeRegression.fit(X_train, y_train)
print("权重向量:%s, b的值为:%.2f" % (ridgeRegression.coef_, ridgeRegression.intercept_))
print("损失函数的值:%.2f" % np.mean((ridgeRegression.predict(X_test) - y_test) ** 2))
print("预测性能得分: %.2f" % ridgeRegression.score(X_test, y_test))
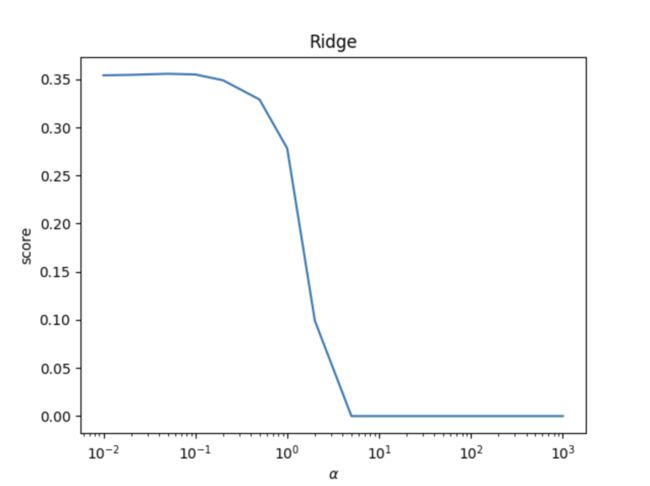
# todo: 测试不同的α值对预测性能的影响
alphas = [0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000]
scores = []
for i, alpha in enumerate(alphas):
ridgeRegression = linear_model.Ridge(alpha=alpha)
ridgeRegression.fit(X_train, y_train)
scores.append(ridgeRegression.score(X_test, y_test))
show_plot(alphas, scores)
# Todo: 分别利用可视化方法和交叉验证法确定惩罚参数λ并建立Lasso回归模型
print('========== ※ Lasso归模型 ※ ==========')
lassoRegression = linear_model.Lasso()
lassoRegression.fit(X_train, y_train)
print("权重向量:%s, b的值为:%.2f" % (lassoRegression.coef_, lassoRegression.intercept_))
print("损失函数的值:%.2f" % np.mean((lassoRegression.predict(X_test) - y_test) ** 2))
print("预测性能得分: %.2f" % lassoRegression.score(X_test, y_test))
# todo: 测试不同的α值对预测性能的影响
alphas = [0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000]
lassos_scores = []
for i, alpha in enumerate(alphas):
lassoRegression = linear_model.Lasso(alpha=alpha)
lassoRegression.fit(X_train, y_train)
lassos_scores.append(lassoRegression.score(X_test, y_test))
show_plot(alphas, lassos_scores)
V、运行结果截图(15分)
VI、结果分析(15分)
。。。。。。(详细分析结果)